
Техническая электродинамика Черенков (Кривець)
.pdf
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
11 |
Безразмерную величину ε, которая определяется формулой
ε = |
εа |
= 1 + k |
|
, |
(1.4) |
|
ε0 |
э |
|||||
|
|
|
|
|||
|
|
|
|
|
называют относительной диэлектрической проницаемостью среды.
Таким образом, в веществе векторы электрической индукции и напряженности электрического поля связаны следующей формулой (материальным уравнением):
D = εa E . |
(1.5) |
1.2.2 Векторы магнитного поля. Для описания магнитного поля (в рамках макроскопической электродинамики) обычно используют следующие два вектора:
H – вектор напряженности магнитного поля размерностью А/м;
B – вектор магнитной индукции размерностью Вб/м2.
Величина вектора магнитной индукции численно равна силе, с которой магнитное поле действует на движущиеся с единичной скоростью перпендикулярно его силовым линиям единичный положительный точечный заряд.
Вектор напряженности магнитного поля вводится аксиоматически в связи с воздействием магнитного поля на атомы и молекулы вещества и вакуума в соответствии со следующей формулой:
|
|
r |
|
r |
|
|
|
|
|
|
H = |
B |
|
− M |
, |
|
|
|
|
|
|
|
|
|||
|
|
µ0 |
|
|
|
|
||
где M – вектор намагниченности вещества, |
µ0- |
магнитная постоянная |
||||||
(погонная индуктивность в вакууме), причем |
|
|
|
|||||
µ |
0 |
= 4π 10 |
−7 Гн |
м |
, |
(1.6) |
||
|
|
|
|
r |
|
|
||
|
|
|
|
|
|
|
|
|
r |
|
|
∑m |
|
|
|
||
M = lim V →0 |
|
i . |
|
|
||||
|
|
r |
|
V |
|
|
|
|
|
|
– магнитный момент i-й молекулы |
||||||
В последней формуле величина mi |
||||||||
(элементарной рамки, обтекаемой |
током |
|
I с |
|
поверхностью S). Внешнее |
|||
магнитное поле оказывает силовое воздействие на рамку, стремясь повернуть ее, ориентируя по полю.
Если магнитное поле не очень сильно, то M = kмH . Отсюда:
r |
B |
r |
|
H = |
− kмH |
||
|
µ0
или
B = µ0 H + kмµ0 H = µ0 (1 + kм )H = µаH ,
где µa = µ0 (1 + kм ) – абсолютная магнитная проницаемость среды, которая измеряется в Гн/м.
12 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
Безразмерную величину µ, которая определяется формулой
µ = |
µа |
= 1 + k |
|
, |
(1.7) |
|
м |
||||
µ0 |
|
|
|
||
|
|
|
|
||
где kм – коэффициент магнитной восприимчивости вещества, называют относительной магнитной проницаемостью среды.
Таким образом, в веществе векторы магнитной индукции и напряженности магнитного поля связаны следующей формулой (материальным уравнением):
B = µa H . |
(1.8) |
По магнитным свойствам вещества делятся на три группы:
диамагнетики (µ < 1), парамагнетики (µ > 1), ферромагнетики (µ >> 1).
1.3. Материальные уравнения. Классификация сред
Электромагнитные взаимодействия между зарядами и токами зависят от свойств среды. Свойства среды характеризуются тремя электродинамическими (макроскопическими) параметрами: εа , µа , σ. Среды принято делить на
однородные и неоднородные, линейные и нелинейные, изотропные и анизатропные.
Среда однородна, если ее электродинамические параметры не зависят от координат. Если хотя бы один из параметров меняется от точки к точке, то среда неоднородна.
Среда линейна, если ее электродинамические параметры не зависят от величин векторов электромагнитного поля. Если хотя бы один из параметров зависит от величин векторов электромагнитного поля, то среда нелинейна.
Среда изотропна, если ее электродинамические параметры не зависят от направления векторов электромагнитного поля. Если хотя бы один из параметров зависит от направления векторов электромагнитного поля, то среда анизатропна.
Электродинамические параметры в каждой точке поля входят в материальные уравнения, связывающие векторы электромагнитного поля. Для случая линейной изотропной среды материальные уравнения имеют следующий вид:
(1.9)
(1.10)
(1.11)
Множитель σ в последнем уравнении имеет размерность См/м и называется удельной проводимостью среды. При σ = const это уравнение выражает закон Ома в дифференциальной форме.
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
13 |
Электродинамические параметры большинства сред в обычных условиях
– скалярные и постоянные величины. При этом соответствующие пары векторов коллинеарные, а их модули связаны линейной зависимостью. При возрастании напряженности поля линейная зависимость нарушается, параметры среды изменяются при изменении напряженности поля, среда становится нелинейной.
В анизотропных средах соотношения между парами векторов зависят от их ориентации. В общем случае эти векторы непараллельные. Для описания свойств анизотропных сред применяют несимметричные тензоры
@εа@,@µа@,@σ@.
Как правило, нелинейность или анизотропия проявляется лишь в одном из материальных соотношений. Соответственно различают нелинейные диэлектрики, анизотропные магнетики и т.п.
В дальнейшем, если не сделано специальных оговорок, среды считаются линейными однородными и изотропными.
1.4.Уравнения Максвелла в дифференциальной и интегральной формах
Макроскопическая теория электромагнетизма основывается на уравнениях Максвелла, которые связывают между собой источники и векторы электромагнитного поля.
Основные законы электричества и магнетизма, кроме закона Фарадея, были получены при наблюдении стационарных полей. С логической точки зрения, априори не следует, что они остаются неизменными для полей, зависящих от времени. Поэтому так велика заслуга Максвелла, который обобщил полученные до него экспериментальные закономерности на случай произвольного электромагнитного поля в произвольной среде, введя всего лишь одно дополнительное слагаемое в закон, открытый Ампером.
Система уравнений электромагнитного поля была постулирована Максвеллом, т.е. введена в теорию аксиоматически. В любой физической теории аксиомами считаются те фундаментальные соотношения, из которых путем лишь математических преобразований выводятся остальные свойства изучаемых объектов. Необъятное количество экспериментальных фактов, полученных после введения этих уравнений, не оставляют сомнений в их правильности, так как выводы электромагнитной теории находятся в неизменном соответствии с результатами опыта и практической деятельности.
Различают уравнения Максвелла в дифференциальной и интегральной формах (см. табл. 1.1). Уравнения Максвелла в дифференциальной форме устанавливают связь между векторами и источниками электромагнитного поля в каждой точке пространства, а уравнения в интегральной форме связывают между собой источники и интегральные характеристики (потоки, циркуляции)
14 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
электромагнитных полей. Переход от одной формы уравнений к другой осуществляется простыми математическими преобразованиями (см. Приложение А).
Таблица 1.1 – Уравнения Максвелла
Уравнения Максвелла в |
Уравнения Максвелла в |
дифференциальной форме |
интегральной форме |
Первое уравнение Максвелла – |
|
закон полного тока Ампера-Максвелла |
|
r r |
|
|
r |
r |
|
d |
|
r |
r |
|
|||||
rotH = j + |
∂D |
|
∫ |
H dl = I + |
|
|
|
∫D dS |
(I) |
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
∂t |
|
L |
|
|
|
dt S |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
Второе уравнение Максвелла |
– закон электромагнитной индукции |
||||||||||||||
|
|
|
|
Фарадея-Максвелла |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
r |
|
|
|
r |
|
r |
|
||||
rotE = − |
∂B |
|
|
∫ |
E dl = − |
d |
|
∫ B dS |
(II) |
||||||
|
|
|
|
|
|
||||||||||
|
|
||||||||||||||
|
∂t |
|
L |
|
dt S |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
Третье уравнение Максвелла – обобщенная теорема Гаусса |
|||||||||||||||
divD = ρ |
|
|
∫ |
r |
|
|
|
|
|
|
(III) |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
D dS = Q |
|
|
|||||||||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
||
|
|
|
Четвертое |
уравнение Максвелла – |
|
|
|
|
|
|
|
||||
|
закон непрерывности магнитного потока |
|
|
|
|
||||||||||
divB = 0 |
|
|
∫ |
B dS = 0 |
|
|
|
(IV) |
|||||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
Поясним физический смысл уравнений Максвелла.
Закон полного тока. Из закона полного тока в дифференциальной форме следует, что вихри магнитного поля возникают только в тех точках пространства, где имеется либо объемная плотность тока
проводимости (j ), либо переменное во времени электрическое поле (∂D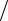 ∂t ≠ 0). Можно
∂t ≠ 0). Можно
сказать иначе. Переменное во времени электрическое поле возбуждает также, как и переменный ток проводимости, переменное во времени магнитное вихревое поле.
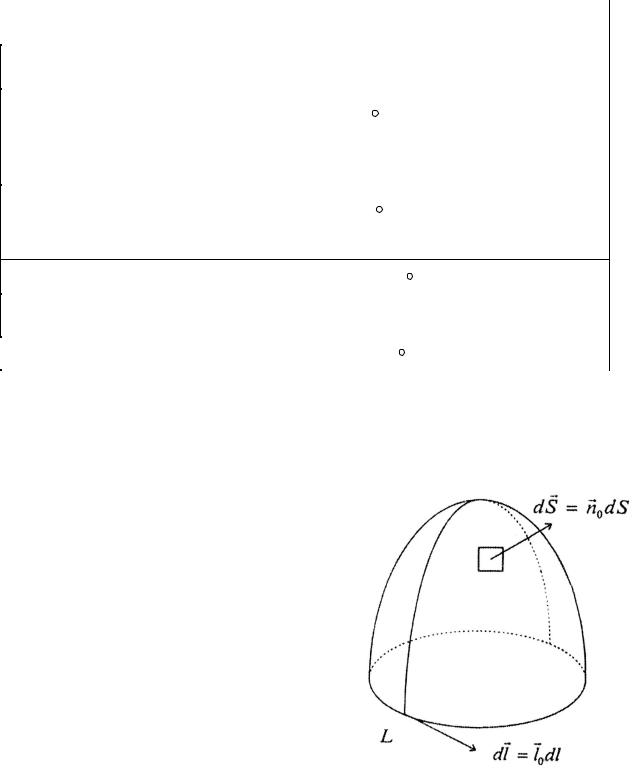
Из закона полного тока в интегральной форме следует, что циркуляция вектора напряженности магнитного поля по любому замкнутому контуру L равна полному току, протекающему через любую поверхность, опирающуюся на этот контур (рис. 1.1).
При этом полным током Iп
Рисунок 1.1 – К пояснению закона полного тока
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
15 |
называется величина, равная:
|
d |
r r |
|
Iп = I + |
∫ D dS . |
||
dt |
|||
|
S |
Соответственно объемная плотность полного тока jn равна:
r |
r |
∂D |
. |
|
j |
= j + |
|||
|
||||
п |
|
∂t |
||
|
|
|||
Величину, определяемую соотношением
r |
∂D |
, |
|
j = |
|||
|
|||
см |
∂t |
||
|
|||
(1.12)
(1.13)
(1.14)
принято называть объемной плотностью тока смещения. Из определения
вектора D следует, что плотность тока смещения определяется движением (смещением) электрических зарядов, связанных в молекулах вещества, и изменением электрического поля в вакууме. Отметим, что закон полного тока был предложен Максвеллом путем обобщения закона Ампера (добавления в правую часть закона Ампера тока смещения) на случай полей, меняющихся во времени по произвольному закону.
Закон электромагнитной индукции. Из закона электромагнитной индук-
ции в дифференциальной форме следует, что вихри электрического поля возникают в тех точках пространства, где имеется переменное во времени магнит-
ное поле (∂B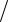 ∂t ≠ 0). Другими словами, переменное во времени магнитное поле
∂t ≠ 0). Другими словами, переменное во времени магнитное поле
возбуждает переменное во времени вихревое электрическое поле.
Из закона электромагнитной индукции в интегральной форме следует,
что циркуляция вектора E по любому замкнутому контуру L равна взятой с обратным знаком скорости изменения магнитного потока, пронизывающего любую поверхность S, опирающуюся на этот контур.
Следует отметить существенную разницу в использовании одного и того же термина контур. В формулировке Фарадея контур – это замкнутая цепь, составленная из проводников. Максвелл обобщил закон Фарадея, понимая под контуром замкнутую линию, произвольно расположенную в пространстве.
Теорема Гаусса. Cоотношение (III) в интегральной форме известно из электростатики, как теорема Гаусса, и обобщено Максвеллом на случай полей, произвольно зависящих от времени. Оно устанавливает, что электрические заряды служат истоками и стоками электрического поля; линии вектора электрической индукции выходят из областей, содержащих положительные заряды и входят в области, где находятся отрицательные заряды.
Из теоремы Гаусса в дифференциальной форме следует, что силовые линии вектора электрического смещения начинаются (заканчиваются) в тех точках пространства, где имеется электрический заряд с объемной плотностью ρ. Точки, в которых силовые линии начинаются (ρ > 0), называются истоками вектора электрического смещения, а точки, в которых силовые линии заканчиваются (ρ < 0), называются стоками того же вектора.
16 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
Из теоремы Гаусса в интегральной форме следует, что поток вектора D через любую замкнутую поверхность S равен алгебраической сумме зарядов, заключенных в объеме V, ограниченном этой поверхностью.
Закон непрерывности магнитного потока. Из четвертого уравнения Максвелла в дифференциальной форме следует, что магнитное поле не имеет ни истоков, ни стоков. Отсюда следует, что силовые линии вектора магнитной индукции всегда замкнуты (поле соленоидально).
Из четвертого уравнения Максвелла в интегральной форме следует, что поток вектора В сквозь любую замкнутую поверхность S всегда равен нулю.
Из уравнений Максвелла можно сделать вывод, что только в случае статических полей, создаваемых неподвижными и неизменными во времени зарядами, электрические и магнитные поля являются независимыми.
В общем случае, когда заряды меняются во времени, электрические и магнитные поля связаны между собой: наличие переменного электрического поля невозможно без существования переменного вихревого магнитного поля и, наоборот.
При решении конкретных задач электродинамики в уравнения Максвелла вводятся сторонние заряды ρст и сторонние токи j ст , которые
являются первопричиной возбуждения электромагнитного поля. Задание сторонних источников производится добавлением в правые части уравнений (I) и (III) соответствующих слагаемых. При этом уравнения Максвелла в дифференциальной форме принимают следующий вид:
r r r |
∂D |
, |
(1.15) |
|||
rotH = j + j ст + |
||||||
|
||||||
|
|
|
∂t |
|
||
r |
|
|
|
|||
rotE = − |
∂B |
, |
|
|
(1.16) |
|
|
|
|
||||
|
∂t |
|
|
|
||
r |
|
|
(1.17) |
|||
divD = ρ + ρст , |
||||||
divB = 0 . |
|
|
(1.18) |
|||
С формальной математической точки зрения уравнения (1.15) – (1.18) являются системой векторно-дифференциальных уравнений для определения
векторов электромагнитного поля по заданным ρст и rj ст . Система уравнений
(1.15) – (1.18) совместно с материальными уравнениями (1.9) – (1.11) является математически полной и позволяет ставить и решать конкретные задачи электродинамики. Используя совместно материальные уравнения и уравнения (1.15) – (1.18), можно получить векторные дифференциальные уравнения,
которым удовлетворяют каждый из векторов Е и Н . В случае однородной изотропной среды без потерь эти уравнения для декартовой системы координат имеют следующий вид:
r |
|
|
∂ |
2 |
E |
|
1 |
gradρст + µ |
|
∂j |
ст |
, |
(1.19) |
E − ε |
µ |
|
|
= |
|
|
|||||||
a ∂t 2 |
|
|
|
|
|||||||||
a |
|
|
εa |
a ∂t |
|
|
|||||||

ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
17 |
|||||||
r |
|
2 |
H |
r |
|
|
||
H − ε |
µ |
|
∂ |
= −rotj |
ст , |
(1.20) |
||
a ∂t2 |
||||||||
a |
|
|
|
|
||||
где – оператор Лапласа, который в декартовой системе координат имеет вид:
∂2 ∂ 2 ∂ 2
=∂x 2 + ∂y 2 + ∂z 2 .
1.5.Граничные условия для векторов электромагнитного поля
Поверхности физических тел являются границами, разделяющими среды с разными свойствами. В рамках макроскопической электродинамики принято считать, что при переходе через эти поверхности параметры сред εа ,µа ,σ
меняются скачком. Такие поверхности называются границами раздела. Согласно уравнениям Максвелла при этом неизбежно испытывают
скачки некоторые векторы поля. Для решения задач электродинамики, помимо уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами в двух очень близких точках, находящихся по обе стороны границы раздела двух сред. Граничные условия являются следствием уравнений Максвелла в интегральной форме.
Пусть достаточно гладкая поверхность S разделяет две среды, в каждой из которых параметры либо постоянны, либо меняются медленно от точки к точке. Тогда в малой окрестности любой точки на поверхности S можно считать границу плоской, а параметры сред – неизменными. Таким образом, из рассмотрения исключаются точки, лежащие вблизи изломов и резких изгибов границы или в области быстрого изменения параметров хотя бы одной из сред.
Рассмотрим некоторую поверхность S, разделяющую две среды с параметрами εa1 , µa1 , σ1 и εa 2 ,µa 2 , σ2 (рис. 1.2).
В каждой точке поверхности S можно провести касательную плоскость
r
P и три единичных вектора: n0 – нормаль, направленная из второй среды в
первую; |
r |
векторы, |
лежащие в плоскости Р (касательные к границе |
|||
N0 , τ0 – |
||||||
раздела). |
При этом будем считать, что |
r |
r |
]. |
||
N0 = [n0 |
, τ0 |
|||||
|
|
|
|
r |
|
|
|
|
|
|
n0 |
|
|
|
|
|
|
Р |
|
S |
|
|
r |
|
|
|
|
|
εa1, µa1,σ a1 |
|
|
|
|
|
|
τ0 |
|
|
|
|
|
|
ε a 2 , µ a 2 ,σ a 2 |
N0 |
|
|
||
Рисунок 1.2 – Две среды, разделенные поверхностью S
18 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
Используя уравнения Максвелла в интегральной форме, можно показать (см. Приложение В), что на поверхности S выполняются следующие равенства:
[r |
|
(r |
|
|
|
|
r |
|
)] |
= 0, |
|
|
|
|||||
n |
, |
E − E |
|
|
|
|
|
|||||||||||
r |
|
0 |
|
|
r 1 |
|
|
|
r |
2 |
|
|
r |
|
|
|
||
[n |
|
, |
(H |
− H |
|
)]= j |
|
, |
(1.21) |
|||||||||
r0 |
|
|
|
r1 |
|
|
|
r |
2 |
|
|
|
s |
|
|
|||
n0 (D1 |
− D2 )= ρs , |
|
|
|||||||||||||||
r |
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|||
|
|
(B |
− B )= 0, |
|
|
|
||||||||||||
n |
|
|
|
|||||||||||||||
|
|
0 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
E |
|
|
− E |
|
|
= 0, |
|
|
|
|
|||||||
|
|
1τ |
|
|
2τ |
|
|
|
|
|
|
|
|
|||||
H |
|
|
− H |
|
|
|
= |
j |
|
|
|
|
||||||
1τ |
2 |
|
|
|
, |
|
|
|
||||||||||
|
|
|
|
|
τ |
|
|
|
|
sN . |
|
(1.22) |
||||||
D1n − D2 n = ρs , |
|
|
|
|||||||||||||||
|
B |
|
|
− B |
|
|
= 0. |
|
|
|
|
|||||||
|
|
1n |
|
|
2n |
|
|
|
|
|
|
|
|
|||||
Соотношения (1.21) называют граничными условиями в векторной, а
соотношения (1.22) – в скалярной форме. Из этих соотношений следует, что касательные составляющие Е1τ и Е2τ вектора E и нормальные составляющие В1n и В2n вектора B при переходе через границу раздела сред всегда непрерывны. Касательные составляющие Н1τ и Н2τ вектора H и нормальные составляющие D1n и D2n вектора D непрерывны только в том случае, если на границе раздела сред отсутствуют соответственно ток с поверхностной плотностью js и заряды с поверхностной плотностью ρs .
Пусть одна из сред, например, вторая является идеальным проводником. Из уравнений Максвелла следует, что в идеальном проводнике (σ = ∞) электромагнитное поле отсутствует. Учитывая этот факт и соотношения (1.21) получаем, что на поверхности идеального проводника граничные условия имеют следующий вид:
r |
, E1 ]= 0, |
r |
D1 |
= ρs , |
r |
, H1 ]= js |
, |
r |
B1 |
= 0 . |
[n0 |
n0 |
[n0 |
n0 |
|||||||
Из последних соотношений |
следует, |
что силовые |
линии вектора E |
|||||||
всегда перпендикулярны, а силовые линии вектора B всегда касательные к поверхности идеального проводника.
Используя граничные условия (1.21), (1.22) и материальные уравнения (1.9), (1.10), можно записать граничные условия для касательных
составляющих векторов D и B и нормальных составляющих векторов E и H .
1.6. Метод комплексных амплитуд
Все реальные электромагнитные процессы можно представить в виде суммы дискретных гармонических колебаний или непрерывного спектра этих колебаний. Поэтому изучают поля при гармонических воздействиях. Такие
поля называют монохроматическими (одноцветными).

|
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
19 |
||
Рассмотрим |
некоторый |
гармонический |
процесс, |
который |
характеризуется следующей функцией Ψ(t): |
|
|
||
|
Ψ(t) = Ψmcos(ωt + ϕ), |
|
(1.23) |
|
где ω = 2π/Т – угловая частота; ϕ – начальная фаза; Ψm – амплитуда гармонического процесса.
В соответствии с методом комплексных амплитуд вместо действительной функции Ψ(t), меняющейся во времени по гармоническому
закону, рассматривается комплексная функция |
|
& |
|
|
|
|
|||
Ψ(t) следующего вида: |
|
||||||||
& |
i (ωt +ϕ ) |
= Ψme |
iϕ |
e |
iωt |
& |
iωt |
, |
(1.24) |
Ψ(t ) = Ψme |
|
|
|
= Ψme |
|
||||
где i = 
 −1 – мнимая единица; Ψ& m – комплексная амплитуда функции Ψ(t). Если комплексная амплитуда известна, то
−1 – мнимая единица; Ψ& m – комплексная амплитуда функции Ψ(t). Если комплексная амплитуда известна, то
|
|
|
& |
iωt |
& |
(1.25) |
|
|
Ψ(t ) = Re[Ψm e |
|
|
]= Re Ψ . |
|||
Вычислим производную по времени от функции Ψ(t). |
|
||||||
|
|
|
|
|
|
& |
|
& |
|
|
|
|
|
|
|
|
dΨ(t ) |
& |
|
iωt |
& |
|
|
|
dt |
|
= iωΨm e |
|
= iωΨ(t ). |
|
|
|
|
|
|
|
|
||
Из последней формулы видно, что операция дифференцирования над |
|||||||
& |
|
|
|
|
|
|
|
комплексной функцией Ψ(t ) заменяется умножением на iω. |
|
||||||
Из формул (1.24) и (1.25) видно, что в комплексной амплитуде |
& |
||||||
Ψm зак- |
|||||||
лючена вся информация об амплитуде и начальной фазе действительной функции Ψ(t). Если к тому же известна частота гармонического процесса, то формула (1.25) позволяет легко определить действительную функцию Ψ(t). Отсюда следует, что при решении конкретных (линейных) задач электродинамики можно рассматривать комплексные функции вида (1.24). При этом сам процесс решения задач существенно упрощается, так как операция дифференцирования над комплексной функцией Ψ& (t ) заменяется умножением на iω.
Изложенное выше остается справедливым и для векторного случая. Рассмотрим гармонический процесс, который характеризуется
векторной гармонической функцией следующего вида:
( ) = r cos(ω + ϕ ) + r cos(ω + ϕ ) + v cos(ω + ϕ ) , (1.26)
A t x0 Axm t x y0 Aym t y z0 Azm t z
где ϕx, ϕy ϕz – начальные фазы, а Axm, Aym, Axm – амплитуды соответствующих проекций вектора A(t ).
В соответствии с методом комплексных амплитуд рассмотрим комплексный вектор:
|
|
r |
r |
|
|
|
& |
& |
|
|
|
A |
= Am exp(iωt ), |
|
где |
|
|
|
|
r |
r |
r |
r |
|
& |
(1.27) |
|||
Am |
= x0 Axm exp(iϕx )+ y0 Aym exp(iϕy )+ z0 Azm exp(iϕz ) |
|||
называется комплексной амплитудой векторной гармонической функции (1.26).
Отметим, что в формуле (1.27) exp(iϕ) ≡ eiϕ .
20 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
Для векторной гармонической функции также имеют место следующие соотношения:
r |
r |
r |
|
|
|
& |
|
& |
(1.28) |
A(t ) = Re A(t ) = Re[Am exp(iωt )], |
||||
|
r |
|
|
|
|
& |
|
r |
|
|
dA(t ) |
& |
|
|
|
|
|
= iωA(t ). |
(1.29) |
|
|
|
||
dt
Отметим еще раз, что решение задач электродинамики для монохроматических полей значительно упрощается при использовании комплексных векторов. Это упрощение, как уже отмечалось, связано с наличием формулы (1.29).
1.7.Уравнения Максвелла для комплексных векторов электромагнитного поля
Уравнения Максвелла являются линейными дифференциальными уравнениями в частных производных с постоянными коэффициентами. Пусть сторонние источники электромагнитного поля являются гармоническими. Очевидно, что и возбужденные ими поля также будут гармоническим, т.е. могут быть записаны в виде (1.26). Как отмечалось в предыдущем параграфе в этом случае вместо действительных векторов вида (1.26) можно использовать комплексные векторы вида (1.27).
Получим уравнения, связывающие между собой комплексные векторы электромагнитного поля для случая линейной изотропной среды. Для этого рассмотрим систему уравнений электродинамики в дифференциальной форме
r r |
r |
∂D |
|
r |
∂B |
r |
|
rotH = j |
ст + j + |
, |
rotE = − |
, divD = ρ + ρст , divB = 0 |
|||
|
∂t |
||||||
|
|
∂t |
|
|
|||
совместно с материальными уравнениями
D = εa E , B = µa H , j = σE .
(1.30)
(1.31)
Пусть среда является однородной. Подставим материальные уравнения (1.31) в уравнения Максвелла (1.30). Тогда получим следующие уравнения:
|
r |
r |
r |
|
|
∂E |
|
r |
|
|
∂H |
|
|
r |
|
ρ + ρ |
ст |
|
||
|
rotH = j ст |
+ σE + ε |
|
|
, rotE = −µ |
|
, divE = |
|
|
, divH = 0 . |
||||||||||
|
а |
|
|
а |
|
|
|
εa |
|
|||||||||||
|
|
|
|
|
∂t |
|
|
∂t |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставим в последние уравнения следующие равенства: |
|
|||||||||||||||||||
|
|
|
r |
|
|
|
r |
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
E(t ) |
& |
|
|
|
& |
(t ). |
|
|
|
|
|
(1.32) |
|||||
|
|
|
= Re E(t ), H (t ) = Re H |
|
|
|
|
|
||||||||||||
Учитывая формулу (1.29) и тот факт, что операцию Re можно вынести за |
||||||||||||||||||||
знак операторов rot и div, получаем следующие соотношения: |
|
|
||||||||||||||||||
r |
r |
r |
r |
|
|
|
r |
|
r |
|
r |
|
& |
& |
ст |
|
r |
|||
& |
& ст |
& |
& |
|
& |
|
& |
& |
|
|
|
|
& |
|||||||
|
|
|
ρ + ρ |
|
|
|
||||||||||||||
rotH = j |
+ σE + iωε аE , rotE = −iωµ |
аH |
, divE = |
|
|
|
|
, divH = 0 . (1.33) |
||||||||||||
εa |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
