Техническая электродинамика Черенков (Кривець)
.pdfТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
151 |
Из последней формулы видно, что с помощью короткозамкнутого шлейфа можно создать реактивную нагрузку любой величины. Например, если величина L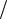 λв изменяется от нуля до 0,25, то входное сопротивление короткозамкнутого шлейфа является индуктивным и изменяется от нуля до бесконечности. Если же величина L
λв изменяется от нуля до 0,25, то входное сопротивление короткозамкнутого шлейфа является индуктивным и изменяется от нуля до бесконечности. Если же величина L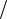 λв изменяется от 0,25 до 0,5, то входное сопротивление короткозамкнутого шлейфа является емкостным и изменяется от бесконечности до нуля.
λв изменяется от 0,25 до 0,5, то входное сопротивление короткозамкнутого шлейфа является емкостным и изменяется от бесконечности до нуля.
Рассмотрим некоторые методы узкополосного согласования.
D.3.1. Согласование с помощью сосредоточенных реактивностей
Этот метод был разработан в 1931 г. В.В. Татариновым и широко применяется практически во всех диапазонах длин волн – от средних до миллиметровых.
Суть метода состоит в следующем. Если линия нагружена на сопротивление, не равное волновому сопротивлению, то в направляющей системе появляется отраженная волна. Включив перед нагрузкой какой-либо реактивный элемент, от которого также отражается волна, можно так подобрать величину реактивного сопротивления (или проводимости) и местоположение этого элемента, что волны, отраженные от нагрузки и отраженные от реактивного элемента, будут иметь одинаковые амплитуды и противоположные фазы. В этом случае их сумма равна нулю (они погашают друга) и в линии от генератора до места включения согласующего элемента отраженной волны не будет.
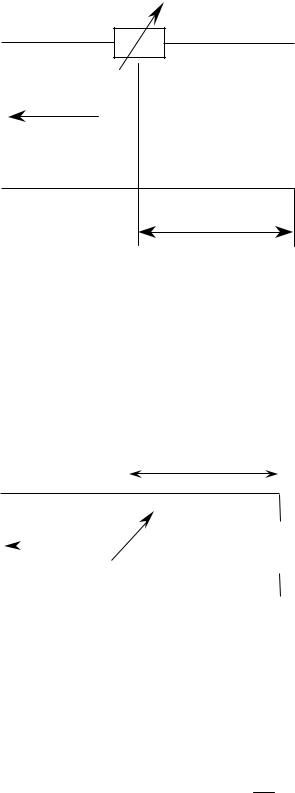
Схемы замещения для последовательной и параллельной реактивностей показаны на рис. D.5 и рис. D.6.
Для настройки линии передачи в режим бегущей волны, в каждой схеме следует выбрать место включения реактивности и ее величину.
Последовательная компенсирующая реактивность ixком (рис. D.5) должна быть включена в такое сечение линии lx , где вещественная часть полного сопротивления точно равна единице (речь идет о нормированном значении). Мнимая часть сопротивления в этой точке в сумме с xком может быть сделана равной нулю, что и обеспечит идеальное согласование на расчетной частоте.

|
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
153 |
||
сопротивлением |
Zв ≠ Rн . Если волновое |
сопротивление трансформатора Zтр |
||
выбрать равным |
|
|
|
|
|
Z тр = |
|
|
|
|
ZвRн |
, |
|
|
то на частоте, |
соответствующей выбранной λв , отражения от |
входа |
||
трансформатора будут отсутствовать. Физически это можно объяснить тем, что на этой частоте происходит компенсация волн, отраженных от нагрузки и входа трансформатора.
Четвертьволновый трансформатор широко используется для соединения двух линий передачи одинакового типа, но с разными волновыми сопротивлениями, величина которых определяется поперечными размерами линий передачи. Например, волновое сопротивление двухпроводной линии и коаксиального кабеля определяются соответственно следующими формулами:
Z |
|
= 276 lg |
D |
, |
Z |
|
= 60 |
µ |
ln |
R2 |
, |
в |
2a |
в |
|
|
|||||||
|
|
|
|
|
ε R1 |
|
|||||
|
|
|
|
|
|
|
|
||||
где D – расстояние между проводами двухпроводной линии; a – радиус проводов;. , ε – относительные магнитная и диэлектрическая проницаемости среды, заполняющей пространство между проводниками коаксиального кабеля; R1 и R2 – радиусы внутреннего и внешнего проводников кабеля.
Конструктивно четвертьволновый трансформатор, например, на основе двухпроводной линии выполняется либо путем изменения расстояния между проводами линии, либо путем изменения диаметра проводов линии.
Отметим, что четвертьволновый трансформатор может быть использован также для согласования комплексных сопротивлений. При этом он располагается в том сечении линии, в котором (в соответствии с формулой (D.14)) ее входное сопротивление чисто активно. В этом случае волновое сопротивление трансформатора Zтр выбирается равным
Z тр = |
|
Z в Rвх |
, |
где Rвх – входное сопротивление |
линии в том сечении, в котором |
||
располагается трансформатор. |
|
|
|
При широкополосном согласовании стремятся к достижению максимальной полосы частот согласования.
В качестве широкополосных согласующих устройств используются ступенчатые и плавные переходы, представляющие собой направляющие системы сложного поперечного сечения, которые также располагаются непосредственно перед нагрузкой. Величина волнового сопротивления перехода (трансформатора) плавно или скачком изменяется от Zв до Rн по
тому или другому закону.
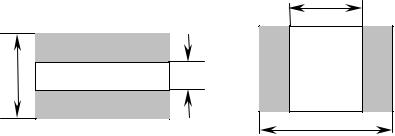
При создании волноводных устройств на базе прямоугольного волновода (фильтры, резонаторы, согласующие устройства и т.д.) в качестве “строительных” элементов широко используются емкостные и индуктивные диафрагмы.
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
155 |
мнимая часть – реактивную мощность, связанную с волной, отраженной в направлении к генератору.
Как уже отмечалось в начале этого приложения, все вышеприведенные факты и формулы соответствуют случаю, когда потери в линии передачи отсутствуют. В линии передачи с потерями амплитуды волн убывают (по мере распространения) по экспоненциальному закону, распределение суммарной амплитуды вдоль направляющей системы носит не периодический характер, понятие КБВ имеет условный смысл и коэффициент полезного действия (КПД) направляющей системы уменьшается с ростом величины потерь.
156 |
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
Приложение Е
МАТЕМАТИЧЕСКИЙ АППАРАТ ЭЛЕКТРОДИНАМИКИ
В настоящем приложении приводятся основные понятия и формулы, касающиеся комплексных чисел, векторной алгебры и векторного анализа.
Е.1. Комплексные числа
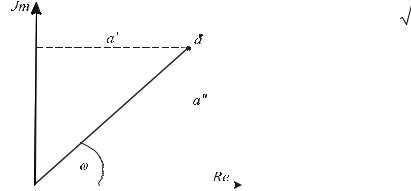
Рассмотрим комплексную плоскость (рис. Е.1). Каждой точке комплексной плоскости соответствует комплексное число a& , которое можно представить в алгебраической либо показательной формах:
a& = a′ + ia′′ , a& = aeiϕ ,
где a′ – действительная часть комплексного числа; a′′ – мнимая часть комплексного числа; i – мнимая единица, определяемая формулами
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = ei |
π |
|
|
|
|
|
|
|
||||
|
|
|
|
|
i i ≡ i2 = −1, |
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|||||||||||||
Из рис. Е.1 и вышеприведенных формул следуют соотношения: |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, ϕ = arctg |
a′′ |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
a′2 |
+ a′′2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a′ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a′ = a cos ϕ , a′′ = a sin ϕ . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Эти |
формулы |
|
позволяют совершить |
||||||||||||||||||
|
|
|
|
|
|
|
|
переход от алгебраической формы записи |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
комплексного числа к показательной форме и, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
наоборот – от показательной к алгебраической. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Сложение |
(вычитание) |
комплексных |
|||||||||||||||||||
|
|
|
|
|
|
|
|
чисел |
|
& |
и |
& |
|
производится |
в |
соответствии с |
||||||||||||||||
Рисунок Е.1 – Комплексная |
|
|
|
a |
b |
|
||||||||||||||||||||||||||
|
|
формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
& |
= с′ + ic′′ = (a′ ± b′) + i(a′′ ± b′′). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
с& = a& ± b |
|||||||||||||||||||||
Умножение комплексных чисел |
|
& |
|
& |
производится в соответствии с |
|||||||||||||||||||||||||||
a и |
b |
|||||||||||||||||||||||||||||||
формулами: |
= c′ + ic′′ = c expiϕ = (a′b′ − a′′b′′)+ i(a′b′′ + a′′b′) = ab exp(i[ϕa + ϕb ]). |
|||||||||||||||||||||||||||||||
& |
||||||||||||||||||||||||||||||||
c& = ab& |
||||||||||||||||||||||||||||||||
Деление |
|
комплексных |
чисел |
& |
|
и |
& |
|
производится |
в |
соответствии с |
|||||||||||||||||||||
|
a |
|
b |
|
||||||||||||||||||||||||||||
формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
a& |
|
a′ + ia′′ |
|
|
a′b′ + a′′b′′ |
|
b′a′′ − a′b′′ |
|
|
a |
|
|
|
( [ |
|
]) |
. |
||||||||||||
|
= & = |
|
= |
|
|
|
|
|
|
|
+ i |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||
|
c |
|
|
b′ |
2 |
+ b′′ |
2 |
|
b′ |
2 |
+ b′′ |
2 |
|
b |
exp i ϕa − ϕb |
|
||||||||||||||||
|
|
|
b b′ + ib′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА |
157 |
Е.2. Векторная алгебра
Рассмотрим вектор A . Его можно представит в общем (некоординатном) виде как A = A0 A , где A0 – орт (единичный вектор), показывающий
направление вектора A ; A – модуль (длина) вектора A .
Вектор A также можно представить в виде суммы трех взаимно перпендикулярных векторов.
В декартовой системе координат (x, y, z) это представление имеет вид
|
|
r |
r |
r |
|
|
A = x0 Ax |
+ y0 |
Ay + z0 Az . |
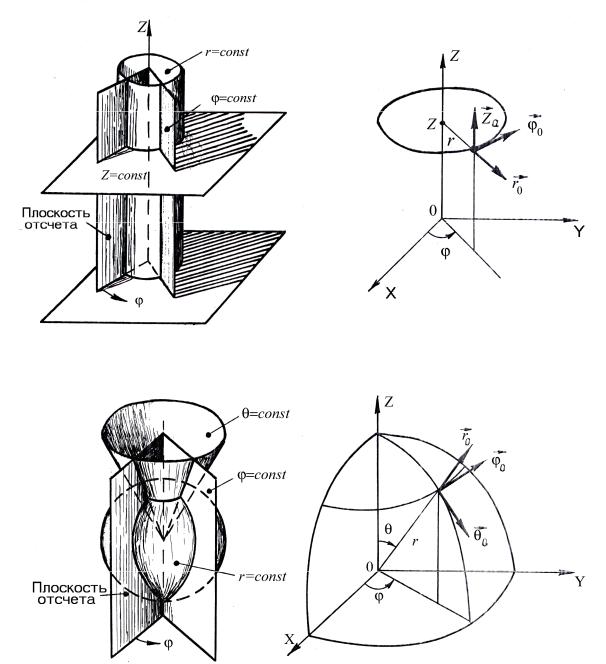
В цилиндрической системе координат ( r , ϕ , θ ) это представление |
||||
имеет вид |
|
r |
r |
r |
|
|
|||
|
|
A = r0 Ar |
+ ϕ0 |
Aϕ + z0 Az , |
где r0 , ϕ0 , z0 |
– |
орты цилиндрической |
системы координат (см. рис. Е.2); |
|
Ar , Aϕ , Az , |
– |
проекции векторов |
на соответствующие направления |
|
цилиндрической системы координат.
В сферической системе координат ( r , ϕ , θ ) это представление имеет
вид |
|
|
r |
|
r |
|
|
|
|
|
|
|
, |
||
|
r |
r |
A = r0 |
Ar |
+ ϑ0 Aϑ + ϕ0 |
Aϕ |
|
|
|
|
|
|
|
||
где |
r0 |
, ϑ0 , ϕ0 |
– орты сферической системы координат (см. рис. Е.3); Ar , Aϑ , Aϕ , – |
||||
проекции векторов на соответствующие направления сферической системы координат.
Рассмотрим векторы A и B . Скалярное и векторное произведение этих
векторов определяются формулами: |
|
|
|
|
||
|
|
r r r r |
|
r |
r |
, |
|
|
(A, B)≡ A B = A B cos A, |
B |
|||
|
|
|
|
|
|
|
r |
r |
– угол между векторами A, B . |
|
|
|
|
где A, |
B |
|
|
|
|
|
|
|
|
|
|
|
|
r r r r |
r |
|
r r |
|
|
[A, B]≡ A × B = n0 |
AB sin A, |
B |
, |
||
|
|
|
|
|
|
где n0 – единичный вектор нормали к плоскости, содержащей векторы A иB , причём A , B и n0 взаимно перпендикулярны и образуют “правую тройку”.
Пусть векторы A и B , представлены через свои проекции в декартовой системе векторов
r |
|
r |
|
r |
|
, B = x B + y B + z B . |
||
A = x A |
+ y A |
+ z A |
||||||
0 |
x |
0 |
y |
0 |
z |
0 x |
0 y |
0 z |