
учебник Кузнецова 2003
.pdf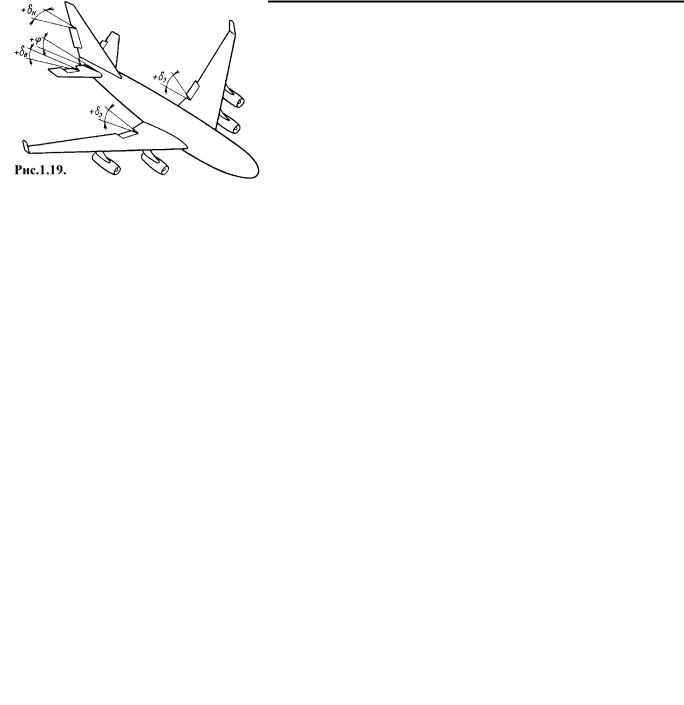
ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИНАМИКИ УПРАВЛЕНИЯ САМОЛЕТОМ
G
появляется плечо аэродинамической силы RA , а, следовательно, и
соответствующий момент. В прямолинейном полете момент Mzα -
основной действующий момент относительно оси OZ . Он существенно преобладает над моментом Mzβ , который возникает вследствие
наличия угла скольжения и связанного с этим несимметричного обтекания самолета воздушным потоком при горизонтальном маневре самолета.
Динамический демпфирующий момент тангажа Mzβ возникает
вследствие вращения самолета вокруг оси OZ . Он создается в основном горизонтальным оперением, а также крылом и фюзеляжем. Изменение угла атаки горизонтального оперения вызывает соответствующее приращение подъемной силы горизонтального оперения. Эта подъемная сила на плече, равном расстоянию от центра масс самолета до точки своего приложения, создает момент тангажа, направленный против вращения самолета. Равнодействующие сил сопротивления воздуха вращению самолета относительно оси OZ в носовой и хвостовой частях фюзеляжа направлены также против вращения самолета и образуют свою составляющую момента тангажа. Крыло создает демпфирующий момент аналогично горизонтальному оперению.
Динамический момент Mzα возникает вследствие того, что при неустановившемся продольном движении самолета изменение угла атаки во времени α вызывает соответствующее изменение скоса потока за крылом. Скошенный воздушный поток достигает горизонтального оперения не мгновенно, а с некоторым запаздыванием по времени. Поэтому угол скоса потока в области горизонтального оперения в каждый момент времени определяется углом атаки, который имело крыло мгновением ранее. Вследствие запаздывания скоса потока угол атаки горизонтального оперения будет отличаться от угла атаки при установившемся движении. Это является причиной появления дополнительной подъемной силы горизонтального оперения и соответствующего
момента Mzα , который противодействует изменению угла атаки и направлен в ту же сторону, что и момент Mzωz .
С учетом рассмотренной структуры составляющих момент тангажа Mz может быть выражен следующим образом:
M |
z |
(β, α, ω ,α,ρ, V) = m |
z |
(β, α,ω ,α)Sb |
a |
ρV2 |
, |
|
||
|
z |
|
z |
2 |
|
(1.28) |
||||
|
|
(β, α, ωz , α) = mzo + mzβ + mzα + mzω |
|
|
||||||
mz |
z |
+ mzα , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
где |
|
mzo , mzβ, mzα , mzω , mzα |
- составляющие коэффициента |
|||||||
|
|
z |
|
|
|
|
|
|
|
|
аэродинамического момента тангажа |
mz , обусловленные соответст- |
|||||||||
венно силой лобового сопротивления при нулевой подъемной силе, углом атаки α , углом скольжения β , скоростью тангажа ωz и скоро-
стью угла атаки α .
Зависимость mz (α,β, ωz , α) в эксплуатационной области режи-
мов линейна и выражается через соответствующие частные производные mαz , mβz , mωz z , mαz . Тогда
Mz (β, α, ωz , α,ρ, V) =
=[mαz + mβz + mωz z + mαz ]Sba ρV2 2 . (1.29)
Типовая зависимость коэффициента аэродинамического момента тангажа mz от угла атаки (рис.1.18) линейна в ограниченном диапазо-
не угла α . Так как mz зависит от сжимаемости воздуха (числа M ), то в выражении (1.28) также необходимо учесть эту зависимость.
Типовые зависимости коэффициента аэродинамического момента тангажа от угла атаки при различных числах М
1.6. УПРАВЛЯЮЩИЕ ВОЗДЕЙСТВИЯ И ВНЕШНИЕ ВОЗМУЩЕНИЯ
Управляющие воздействия. Существуют два основных способа аэродинамического управления движением самолета. Первый предусматривает управление аэродинамическими моментами путем отклонения пилотом или автоматикой моментных органов управления: элеронов, рулей направления и высоты. Второй способ предусматривает управление аэродинамическими силами путем отклонения пилотом или автоматикой органов управления силами: тормозных щитков, интерцепторов, закрылков, подфюзеляжного руля совместно с рулем направления и т.д. В первом способе управления различают четыре основных
управляющих воздействия: по аэродинамическому моменту крена δэ ,
аэродинамическому моменту рыскания δн , аэродинамическому мо-
менту тангажа δв и ϕ .
Управляющее воздействие по крену - угол отклонения элеронов δэ
для создания аэродинамического момента крена (рис. 1.19). Угол отклонения элеронов считается положительным при повороте правого элерона по часовой стрелке, а левого против часовой стрелки, если
смотреть в направлении связанной оси OZ .
Для создания положительного угла отклонения элеронов при ручном управлении необходимо повернуть штурвал против часовой стрелки. Тогда правый элерон пойдет вниз, а левый - вверх. Это приведет к увеличению подъемной силы на полукрыле с отклоненным вниз элероном и уменьшению подъемной силы на полукрыле с отклоненным
вверх элероном. Пара сил ∆Yэ создает управляющий аэродинамиче-
ский момент крена на плече zэ :
M |
xδэ |
= 2∆Y z |
э |
= Mδэ δ |
э |
= mδэ qSlδ |
, (1.30) |
|
|
э |
x |
x |
э |
|
|||
где Mδxэ - частная производная аэродинамического момента крена
по отклонению элеронов; mδxэ - коэффициент эффективности элеронов по крену.
Производная mδxэ отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента крена mx , при отклонении элеронов на 1 ° (рис. 1.20).
11 |
апрель 2003г. |

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ
При отклонении элеронов помимо аэродинамического момента возникает также аэродинамический момент рыскания, создаваемый
приращением лобового сопротивления ∆Xэ на плече zэ :
M δ = 2∆X z = Mδэ δ = mδэ qSlδ , (1.31)
y э э э y э y э
где Mδyэ - частная производная аэродинамического момента рыс-
кания по отклонению элеронов; mδyэ - коэффициент эффективности элеронов по рысканию.
Производная mδyэ отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента рыскания при отклонении элеронов на 1°.
Отклонение элеронов нарушает равновесие моментов относительно
оси OX , и самолет под действием момента Myδэ поворачивается вокруг этой оси. GНачинает меняться угол крена γ , и вектор аэродина-
мической силы Yа , лежащий в продольной плоскости самолета, дает
проекцию на горизонтальную плоскость Yа sin γ . Эта проекция явля-
ется центростремительной силой, искривляющей траекторию полета.
Управляющее воздействие по рысканию - угол отклонения руля на-
правления δн для создания аэродинамического момента рыскания. Этот угол считается положительным при повороте руля против часовой стрелки, если смотреть в направлении связанной оси OY (см. рис.
1.19).
Для создания положительного угла отклонения руля направления при ручном управлении необходимо правую педаль отклонить от себя, а левую - на себя. Тогда руль направления пойдет вправо. Это приведет
к появлению поперечной силы Zн , которая создаст управляющий аэ-
родинамический момент рыскания Myδн на плече Lн :
Myδн = ZнLн = Mδyн δн = mδyн qSlδн, (1.32)
где Mδyн - частная производная аэродинамического момента рыс-
кания по отклонению руля направления; mδyн - коэффициент эффективности руля направления по рысканию.
Производная mδyн отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента рыскания my при отклонении
руля направления на 1° (рис. 1.21). При отклонении руля направления помимо аэродинамического момента рыскания возникает также аэро-
динамический момент крена, создаваемый поперечной силой Zн на плече yн :
Mxδн = Zнyн = Mδxн δн = mδxн qSlδн, (1.33)
где Mδxн - частная производная аэродинамического момента крена
по отклонению руля направления; mδxн - коэффициент эффективности руля направления по крену.
Производная mδxн отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента крена mx при отклонении
руля направления на 1°.
Отклонение рулей направления вызывает нарушение равновесия моментов относительно оси OY . Самолет поворачивается вокруг этой оси и возникает угол скольжения β , а вместе с ним и аэродинамиче-
ская боковая сила Zа , которая является центростремительной силой, искривляющей траекторию полета.
Так как центростремительная сила, возникающая при отклонении элеронов, существенно больше центростремительной силы, возникающей при отклонении рулей направления, управление траекторией в горизонтальной плоскости посредством элеронов является более предпочтительным, за исключением тех случаев, когда диапазон допустимых углов крена самолета ограничен (взлет, посадка). Кроме того, полет со скольжением вызывает дискомфорт экипажа и пассажиров. Поэтому управление в горизонтальной плоскости обычно осуществляется без скольжения (координированно). Это достигается одновременным отклонением рулей направления и элеронов. Чтобы при этом не возникало потери высоты вследствие уменьшения проекции аэродинамической силы на вертикальную плоскость, необходимо одновременно отклонить рули высоты вверх.
Управляющее воздействие по тангажу - угол отклонения рулей высоты δв , для создания аэродинамического момента тангажа. Этот угол считается положительным при повороте руля по часовой стрелке, если смотреть в направлении связанной оси OZ (см. рис. 1.19).
Для создания положительного угла отклонения рулей высоты при ручном управлении необходимо отклонить колонку штурвала от себя, тогда рули высоты пойдут вниз. Это приведет к увеличению подъемной
силы на горизонтальном оперении ∆Yго , которая создаст управляю-
щий аэродинамический момент тангажа Mzδв на плече Lго :
M |
zδв |
= ∆Y L |
го |
= Mδв δ |
в |
= mδв qSb |
δ |
, (1.34) |
|
го |
z |
z a |
в |
|
где Mδzв - частная производная аэродинамического момента тан-
гажа по отклонении рулей высоты; mδzв - коэффициент эффективности рулей высоты по тангажу.
Производная mδzв отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента тангажа mz при отклонении
рулей высоты на 1° (рис. 1.22).
Управляющее балансировочное воздействие по тангажу - угол от-
клонения стабилизатора ϕ для создания аэродинамического момента
тангажа. Он положителен, если задняя кромка стабилизатора отклоняется вниз (см. рис. 1.19).
Для создания положительного угла отклонения стабилизатора при ручном управлении необходимо отжать гашетку управления стабилизатором от себя, тогда задняя кромка стабилизатора пойдет вниз. Это приведет к увеличению подъемной силы на горизонтальном оперении
∆Yго , которая создаст управляющий балансировочный момент тан-
гажа Mzϕ на плече Lс : |
|
|
||||
M |
zϕ |
= ∆Y L |
c |
= Mϕϕ = mϕqSb |
ϕ, (1.35) |
|
|
го |
z |
z a |
|
||
где Mϕz - частная производная аэродинамического момента танга-
12 |
май 2003г. |

ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИНАМИКИ УПРАВЛЕНИЯ САМОЛЕТОМ
жа по отклонению стабилизатора; mϕz - коэффициент эффективности стабилизатора по тангажу.
Производная mϕz отрицательна и показывает, как изменяется ко-
эффициент аэродинамического момента тангажа mz при отклонении стабилизатора на 1°.
Отклонение рулей высоты или стабилизатора вызывает нарушение равновесия моментов относительно оси OZ и вследствие действия
управляющих моментов Mzδв или Mzϕ самолет поворачивается
вокруг этой оси. При этом начинают меняться углы тангажа ϑ и атаки α . Изменение угла атаки приводит к изменению аэродинамической
подъемной силы Ya . Равновесие между подъемной силой и силой
тяжести нарушается и под действием центростремительной силы самолет искривляет траекторию движения в вертикальной плоскости.
Таким образом, отклонения рулей и стабилизатора создают управляющие моменты благодаря сравнительно небольшим управляющим силам на значительных плечах. Под действием этих моментов самолет изменяет свое угловое положение, что приводит уже к изменению величины аэродинамической силы за счет изменения углов атаки и скольжения, т.е. управление аэродинамическими силами осуществляется косвенно через управление угловым положением (ориентацией) самолета.
Второй способ аэродинамического управления движением самолета путем непосредственного создания аэродинамических сил предусматривает три основных управляющих воздействия: по силе лобового
сопротивления δx , аэродинамической подъемной силе δy и аэроди-
намической боковой силе δz .
Управляющее воздействие по силе лобового сопротивления - угол отклонения δx , органов непосредственного управления силой лобово-
го сопротивления (например, тормозных щитков) для создания ее приращения.
Для создания положительного воздействия δx необходимо выпус-
тить тормозные щитки. Это приводит к увеличению силы лобового сопротивления на величину управляющей силы лобового сопротивления
Xaδx = |
δx |
δx |
δx |
|
Xa |
= cxa qSδx , (1.36) |
|
||
где Xaδx |
-частная производная силы лобового сопротивления по |
|||
|
|
|
δx |
- коэффициент эффективности |
отклонению органов управления; cxa |
||||
органов непосредственного управления силой лобового сопротивления.
Управляющее воздействие по аэродинамической подъемной силе -
угол отклонения δy органов непосредственного управления подъем-
ной силой (например, интерцепторов) для создания ее приращения. Для создания положительного воздействия необходимо отклонить
интерцепторы из выпущенного положения вниз. В результате подъем-
ная сила увеличивается на управляющую аэродинамическую подъемную силу Yaδy :
Y |
= Yδy δ |
y |
= cδy qSδ |
y |
, (1.37) |
aδy |
a |
xa |
|
где Yaδy - частная производная аэродинамической подъемной си-
δy |
|
лы по отклонению органов управления; cxa |
-коэффициент эффектив- |
ности органов непосредственного управления подъемной силой.
Управляющее воздействие по аэродинамической боковой силе -
угол отклонения δz органов непосредственного управления аэродина-
мической боковой силой (например, подфюзеляжного носового руля совместно с рулем направления) для создания ее приращения.
Для создания положительного воздействия δz необходимо одно-
временно отклонить подфюзеляжный носовой руль и руль направления вправо. Это увеличивает аэродинамическую боковую силу на управ-
ляющую аэродинамическую боковую силу Zaδz :
Zaδz = |
δz |
δz |
δz |
|
Za |
= cxa qSδz , (1.38) |
|
||
где Zaδz |
- частная производная аэродинамической боковой силы по |
|||
|
|
|
δz |
- коэффициент эффективности |
отклонению органов управления; cxa |
||||
органов непосредственного управления боковой силой. Непосредственному управлению аэродинамическими силами свой-
ственна существенно меньшая инерционность по сравнению с управлением путем изменения аэродинамических моментов. Помимо аэродинамических способов управления движением самолета другим основным способом является непосредственное управление тягой.
Управляющее воздействие по тяге – угол отклонения рычагов управления двигателями δP для создания приращения тяги.
Для создания положительного воздействия по тяге необходимо отклонить рычаги от себя. Это приводит к увеличению тяги на величину
управляющей тяги PδP :
PδP = PδP δP = cδPP qSδP ,
где PδP - частная производная тяги по отклонению рычагов управ-
ления двигателями; cδPP - коэффициент эффективности рычагов управления двигателями.
Управляющее воздействие по тяге δP кроме управляющей тяги
PδP создает также и управляющий момент тангажа тяги:
MP |
= MδPP δP = cδPP qSyPδP (1-40) |
z |
z |
где MδP - частная производная проекции момента тяги на связан-
Pz
ную ось OZ по отклонению рычагов управления двигателями.
Внешние возмущения. Все возмущения, действующие на самолет в полете, можно условно разделить на две группы возмущений. К первой группе относятся возмущения, связанные с изменением состояния самолета: выпуском механизации крыла и шасси, отказом двигателя и т. д. Ко второй группе возмущений относятся возмущения, связанные с изменением состояния окружающей среды: ветром, турбулентностью атмосферы и т. д. Для учета влияния на движение самолета возмущений первой группы их действие приводят к удобному для исследований виду - внешним силам и моментам. G
Результирующая внешняя сила Fв - главный вектор системы внешних сил, действующих на самолет вследствиеG изменения его состояния. Результирующая внешняя сила Fв определяется проекциями на оси связанной системы координат: внешней продольной силой fx ,
внешней нормальной силой fy и внешней поперечной силой fz .
Внешняя сила Fв изменяет силу лобового сопротивления, аэродинамические подъемную и боковую силы следующим образом:
Xafx |
fx |
fx |
fx |
|
|
|
= Xa |
= cxa qSfx ; |
|||||
Y |
= Yfy f |
y |
= cfy qSf |
y |
; |
|
afy |
a |
|
xa |
(1.41) |
||
Zafz |
fz |
|
|
fz |
|
|
|
|
|
|
|||
= Za fz = cxa qSfz , |
|
|||||
где Xfx , Yfy |
, Zfz - частные производные силы лобового сопро- |
|||||
|
a |
a |
|
a |
|
|
тивления, аэродинамических подъемной и боковой сил соответственно
13 |
апрель 2003г. |
В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ
по внешним продольной, нормальной и поперечной силам; атаки
fx |
fy |
fz |
- частные производные коэффициентов силы лобового |
cxa |
,cya |
,cza |
сопротивления, аэродинамических подъемной и боковой сил по составляющим внешней силы.
Зависимости аэродинамических сил от внешних сил можно считать линейными, определяемыми соответствующими частными производными.
Результирующий внешний момент
внешних моментов, действующих на самолет вследствие изменения его состояния. Он определяется проекциями на оси связанной системы
координат: внешними моментом крена mxв , моментом рыскания
myв и моментом тангажаG myв .
Внешний момент Mв изменяет аэродинамические моменты крена,
рыскания и тангажа следующим образом:
Mxв = Mmx в mxв = mmx в qSlmxв ,
Myв = Mmy в myв = mmy в qSlmyв ,
Mzв = Mmz в mzв = mmz в qSba mzв . (1.42)
Сучетом управляющих воздействий и внешних возмущений аэродинамические силы, действующие на самолет, имеют вид:
Xa = Xaα + XaM + Xaδx + Xafx ;
Ya = Yaα + YaM + Yaδy + Yafy ;
Za = Zaβ + Zaδz + Zafz . (1.43)
С учетом управляющих воздействий и внешних возмущений аэродинамические моменты, действующие на самолет, определяют следующим образом:
Mx = Mxβ + Mxα + Mxωx +
Mxωy + Mxδ' э + Mxδн + Mxв ; My = Myβ + Myα + Myωx +
Myωy + Myδ' э + Myδн + Myв ;
Mz = Mz0 + Mzα + Mzβ +
Mzωz + Mzα + Mxδв + Mzϕ + Mzв . (1.44)
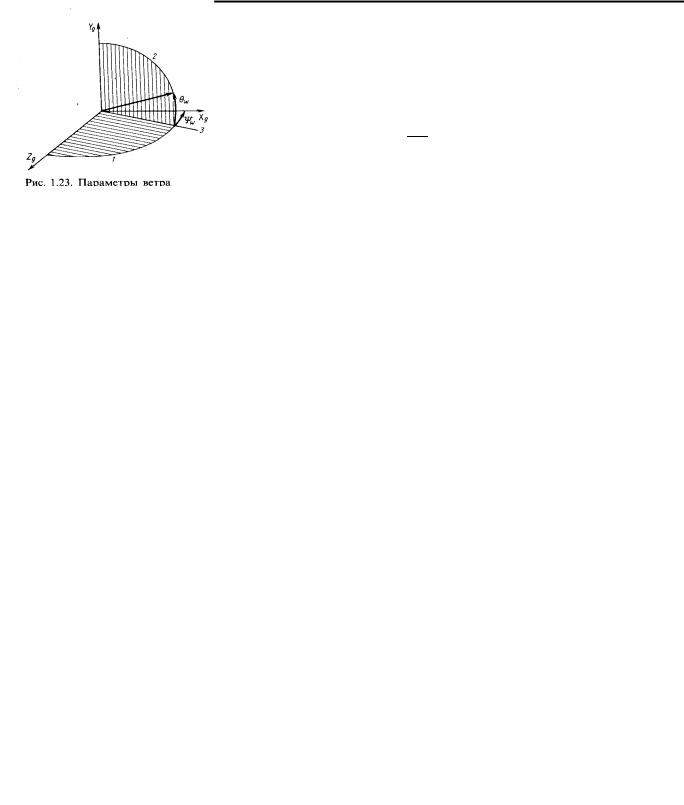
Вкачестве основного внешнего возмущения со стороны окружающей среды рассмотрим действие ветра, которое характеризуется следующими параметрами (рис. 1.23).
G
Скорость ветра W - скорость среды, не возмущенной самолетом, относительно какой-либо из земных координат. Ее можно определить в
виде проекций на соответствующие оси Wx , Wy , Wz . Угол ветра
ΨW - угол между осью OX нормальной системы координат и проек-
G
цией скорости ветра W на горизонтальную плоскость OXg Zg нор-
мальной системы координат. Наклон ветра θW -угол между направле-
G
нием скорости ветра W и горизонтальной плоскостью.
При исследовании динамики движения самолета действие ветра в вертикальной плоскости удобно учитывать в виде приращения угла
αW = arctg |
Wy |
= arctg |
Wy |
, (1.45) |
V |
V0 + W |
|||
|
к |
|
x |
|
где V0 - опорное значение воздушной скорости. В силу того, что V0 >> Wx , и V0 >> Wy ,
αW = WV0y . (1.46)
Тогда угол атаки самолета с учетом действия ветра
α = α − αW . (1.47)
Аналогичным образом действие ветра в горизонтальной плоскости удобно учитывать в виде приращения угла скольжения
βW = −arctg |
Wz |
= −arctg |
Wz |
= − |
Wz |
. (1.48) |
V |
V0 + W |
V0 |
||||
|
к |
|
x |
|
|
|
Тогда с учетом действия ветра угол скольжения самолета
β = β−βW . (1.49)
14 |
май 2003г. |

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА
Глава 2. |
|
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТРАНСТ- |
ωyк |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ВЕННОГО ДВИЖЕНИЯ САМОЛЕТА |
|
|
|
= Ψcos θ; |
(2.4) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
= θ. |
|
|
|
|
|
|
|
|||
2.1. УРАВНЕНИЯ ДВИЖЕНИЯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
zк |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примем допущение об отсутствии ветра, тогда значение земной |
||||||||||||
Пространственное движение самолета описывается системой диф- |
скорости |
V совпадает со значением воздушной скорости Vк = V и |
||||||||||||||||||||||||||||||||
ференциальных уравнений. В главе 1 были введены понятия собствен- |
|
|
|
к |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ного и вынужденного, поступательного и вращательного движений |
векторное уравнение (2.1) с учетом уравнений (2.2) - (2.4) примет сле- |
|||||||||||||||||||||||||||||||||
самолета. Вывод уравнений удобно провести отдельно для каждого из |
дующий скалярный вид: |
|
|
|
|
|
||||||||||||||||||||||||||||
перечисленных видов движения с последующим их объединением в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
общую математическую модель пространственного движения самолета. |
mV = Fxк ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Уравнения собственного поступательного движения. Собствен- |
mVθ = F |
; |
|
|
|
(2.5) |
|
|||||||||||||||||||||||||||
ное поступательное движение самолета описывается системой динами- |
|
|
|
yк |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ческих и кинематических дифференциальных уравнений. Динамиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ские уравнения описывают движение центра масс самолета относи- |
−mVΨcos θ = Fzк , |
|
|
G |
|
|||||||||||||||||||||||||||||
тельно Земли и позволяют установить зависимость между параметрами |
где Fxк , Fyк , Fzк |
|
|
|
|
|
||||||||||||||||||||||||||||
поступательного движения самолета относительно Земли (земной ско- |
- |
проекции вектора сил Fк на оси траекторной |
||||||||||||||||||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
Ψ , |
|
|
|
|
|
θ ) и пара- |
системы координат. |
|
|
|
|
|
|
|
|
||||||||
ростью |
V |
|
|
, |
углом пути |
углом наклона траектории |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим правую часть системы уравнений (2.5). Движение цен- |
||||||||||||||
метрами движения самолета относительно воздушного потока (углом |
тра масс самолета в основном определяется действием трех видов сил: |
|||||||||||||||||||||||||||||||||
атаки α , углом скольжения β , скоростным углом крена γa ). |
вектора тяги двигателей P , |
вектора аэродинамической силы RA и |
||||||||||||||||||||||||||||||||
Динамические уравнения получаются из векторного уравнения для |
|
|
|
|
|
|
|
|
|
|
|
G |
|
|||||||||||||||||||||
количества движения относительно центра масс самолета: |
|
вектора силы тяжести самолета G . Спроецировав эти силы на оси |
||||||||||||||||||||||||||||||||
|
|
G |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
траекторной системы координат, получим: |
|
|||||||||||||
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
m |
|
к |
= F , (2.1) |
|
|
|
|
|
|
|
|
|
|
F |
|
= P |
+ R |
|
|
+ G |
|
; |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Axк |
|
|
|||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
xк |
|
xк |
|
|
|
|
xк |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fyк |
= Pyк |
+ RAyк |
+ Gyк ; (2.6) |
|
||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
где |
|
- |
масса самолета; F |
- вектор сил, действующих на само- |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
F |
|
= P |
+ R |
|
|
+ G |
|
. |
|
|||
лет в траекторной системе координат. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
От векторного уравнения (2.1) перейдем к скалярным уравнениям. |
zк |
|
zк |
|
Azк |
|
zк |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
При этом мы пренебрегаем действием кориолисовой силы инерции |
||||||||||||
Для этого определим проекции вектора dVк |
/ dt на соответствующие |
и переносной силы инерции, связанных с вращением Земли. Для полу- |
||||||||||||||||||||||||||||||||
оси. Так как траекторная система координат вращается относительно |
чения проекций вектора тяги |
P воспользуемся матрицей направляю- |
||||||||||||||||||||||||||||||||
нормальной с угловой скоростью |
G |
, проекции производной вектора |
щих косинусов (табл.П1 Приложения), позволяющей перейти от свя- |
|||||||||||||||||||||||||||||||
ωк |
||||||||||||||||||||||||||||||||||
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
занной системы координат к траекторной: |
|
||||||||||||
Vк можно определить следующим образом: |
|
|
|
Pxк |
= P cos αcosβ; |
|
|
|
|
|||||||||||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
dVк |
|
|
|
|
+ ωyк Vzк |
− ωzк |
Vyк ; |
|
|
|
Py |
|
= P(sin αcos γa + cos αsin βsin γa ); (2.7) |
|
||||||||||||||||||||
|
dt |
|
|
|
|
= Vxк |
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pzк |
= P(sin αsin γa − cos αsin βcos γa ). |
|
||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
dVк |
|
|
|
|
+ ωzк |
Vxк |
− ωxк |
Vzк ; |
|
|
|
В уравнениях (2.7) предполагается, что тяга двигателей P , |
лежа- |
|||||||||||||||||||||
|
dt |
|
|
|
|
= Vук |
|
|
|
щая в плоскости симметрии самолета XOY составляет с осью |
OX |
|||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол ϕP = 0 . В противном случае этот угол необходимо прибавить к |
||||||||||||
dVк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
углу атаки α . |
|
|
|
|
|
|
|
|
|
||||||||
|
|
dt |
|
|
|
|
= Vzк |
|
+ ωxк |
Vyк |
− ωyк |
Vxк , (2.2) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
Для получения проекций вектора аэродинамической силы RA на |
|||||||||||||||
где Vzк , Vxк ,Vyк |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
- проекции вектора скорости Vк на оси траек- |
траекторные оси координат воспользуемся допущением об отсутствии |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ветра. Тогда траекторная система повернута относительно скоростной |
||||||||||||
торной системы координат; Vzк , Vxк ,Vyк |
- |
проекции производной |
на угол |
γa вокруг оси |
OXa . Поэтому проекции аэродинамической |
|||||||||||||||||||||||||||||
вектора |
скорости |
|
на |
оси |
|
траекторной |
системыG |
координат; |
силы RA на оси траекторной системы координат выражаются через |
|||||||||||||||||||||||||
ωxк ,ωyк ,ωzк |
- проекции вектора угловой скорости ωк |
вращения |
проекции на скоростные оси: |
|
|
|
||||||||||||||||||||||||||||
траекторной системы координат относительно Земли на траекторные |
RAxк |
= −Xa ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С |
|
учетом |
|
того, |
|
что |
|
Vxк |
= Vк , Vyк = Vzк = 0, |
RAyк |
= Ya cos γa − Za sin γa ; (2.8) |
|
||||||||||||||||||||||
|
|
|
|
|
|
= 0, уравнения (2.2) упрощаются следующим образом: |
RAzк |
= Ya sin γa + Za cos γa . |
|
|||||||||||||||||||||||||
Vyк = Vzк |
|
|||||||||||||||||||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
Сила тяжести самолета G приложена в его центре масс и направ- |
||||||||||||
dVк |
|
|
|
dVк |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
= Vк |
, |
|
|
|
|
|
= ωzк |
Vк; |
|
|
|
лена вниз по местной вертикали. Следовательно, она расположена в |
|||||||||||||||
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
плоскости |
OXкYк |
|
траекторной системы координат и ее проекции |
|||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеют вид: |
|
|
|
|
|
|
|
|
|
|
|||||
dVк |
|
|
= −ω |
|
V . |
|
|
|
|
|
|
|
(2.3) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
= −mgsin θ; |
|
|
|
|
|
|||||||||||||||
|
dt |
|
|
|
|
|
yк |
к |
|
|
|
|
|
|
|
|
|
xк |
|
|
|
|
|
|||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −mg cos θ; (2.9) |
|
|
||||||||||||
Определим кинематическую связь проекций вектора ωк угловой |
Gyк |
|
|
|||||||||||||||||||||||||||||||
скорости вращения траекторной системы координат относительно нор- |
Gzк |
= 0. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
мальной с углами и их производными, характеризующими положение |
Подставим выражения (2.6) - (2.9) в правую часть системы уравне- |
|||||||||||||||||||||||||||||||||
траекторной системы координат относительно нормальной: |
|
|||||||||||||||||||||||||||||||||
|
ний (2.5). Тогда, с учетом зависимости сил от параметров движения |
|||||||||||||||||||||||||||||||||
ωxк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= Ψsin θ; |
|
|
|
|
|
|
|
|
|
|
|
|
(1.8), (1.11) - (1.13), получим следующую систему динамических урав- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нений собственного поступательного движения центра масс самолета в |
||||||||||||
проекциях на оси траекторной системы координат
______________________________________________________________________________________________________________________________
15
апрель 2003г.

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ
mV = P(M, pH ,TH ,ρ, V)cos αcosβ
−Xa (α,M,ρ, V) − mgsin θ = Fxк (α,β,θ, M,V,ρ,pH ,TH ),
mVθ = P(M,pH ,TH ,ρ,V) [sin αcos γa + cos αsin βsin γa ] +
+Ya (α, M,ρ,V)cos γa − Za (β,ρ,V)sin γa − −mg sin θ = Fyк (α,β,θ, γa ,M, V,ρ, pH ,TH ),
mVΨcos θ = P(M,pH ,TH ,ρ,V) [sin αsin γa −
−cos αsin βcos γa ] +Ya (α, M,ρ,V)sin γa + Za (β,ρ, V)cos γa = Fzк (α,β,θ, γa , M,V,ρ, pH ,TH ). (2.10)
Продолжим построение математической модели собственного поступательного движения самолета, дополнив систему динамических уравнений (2.10) кинематическими уравнениями. Эти уравнения позволяют установить зависимость между параметрами положения самолета в поступательном движении относительно Земли (пройденным рас-
стоянием L , боковым отклонением z , высотой полета H ) и параметрами этого движения (воздушной скоростью V , углом пути Ψ и углом наклона траектории θ ).
Кинематические уравнения поступательного движения описывают движение центра массG самолета относительно Земли. Вектор земной
скорости самолета Vк определяется проекциями на нормальные оси с
помощью таблиц направляющих косинусов (табл.П1 Приложения). Учтем тот факт, что оси нормальной системы координат парал-
лельны осям нормальной земной системы координат. При допущении отсутствия ветра Vк = V координаты самолета в нормальной системе
координат xg , yg , zg удобно заменить на параметры положения самолета L, H, z . Тогда:
dxdtg = dLdt = V cos θcos Ψ = L; dydtg = dHdt = V sin θ = H;
dzdtg = dzdt = −V cos θsin Ψ = z. (2.11)
Система динамических уравнений (2.10) и система кинематических уравнений (2.11) представляют собой математическую модель собственного поступательного движения самолета.
Уравнения собственного вращательного движения. Собствен-
ное вращательное движение самолета описывается системой динамических и кинематических дифференциальных и алгебраических уравнений. Динамические уравнения описывают движение самолета относительно его центра масс и позволяют установить взаимосвязь парамет-
ров вращательного движения самолета (скоростей крена ωx , рыскания
ωy и тангажа ωz ).
Динамические уравнения получают из векторного уравнения для
главного кинематического момента относительно центра масс количе- |
|||
|
|
|
G |
ства движения самолета как твердого тела K : |
|||
|
dKG |
|
G |
|
|
= MR . (2.12) |
|
|
dt |
||
|
|
|
|
От векторного уравнения (2.12) перейдемGк скалярным уравнениям. |
|||
Для этого |
определим проекции вектора dK / dt на оси связанной |
||
системы координат. Так как проекции производнойG вектора K зависят от составляющих угловой скорости ω вращения связанной систе-
мы координат относительно Земли, то система скалярных уравнений |
|||
определяется следующим образом |
|||
|
G |
|
|
dK |
|
||
|
|
|
= Кx + ωyKz − ωz Ky ; |
|
|||
dt |
x |
|
|
dK |
|
||
|
|
|
= Кy + ωz Kx − ωx Kz ; |
|
|||
|
dt y |
|
|
dK |
|
||
|
|
|
= Кz + ωx Ky − ωyKx , (2.13) |
|
|||
|
dt z |
|
|
где Kx ,Ky , Kz - проекции вектора кинетического момента само-
лета K на оси связанной системы координат; Кx , Кy , Кz - проекции
производной вектора кинетического момента самолета на оси связанной системы координат. G
Проекции вектора кинетического момента K на оси связанной системы координат имеют вид:
Kx = Jx ωx − Jxyωy − Jxzωz ;
Ky = −Jxyωx + Jyωy − Jyzωz ;
Kz = −Jxzωx − Jyzωy + Jzωz , (2.14)
где Jx , Jy ,Jz - осевые моменты инерции самолета; Jxy , Jxz ,Jyz
- центробежные моменты инерции самолета.
Моменты инерции самолетов с меняющейся в полете массой вследствие выгорания топлива являются в общем случае функциями времени, однако мы этой зависимостью пока будем пренебрегать.
Поскольку основная плоскость OXY связанной системы координат является плоскостью симметрии самолета, то центробежные мо-
менты инерции, содержащие координаты z , равны нулю: Jxz = Jyz =0.
Тогда система уравнений (2.13) упрощается:
|
dK |
|
= Jx ωx − Jxyωy + (Jz − Jy )ωyωz + Jxyωx ωy ; |
|
|
|
|||
dt |
||||
|
x |
|
||
|
dK |
|
= Jyωy − Jxyωx + (Jz − Jz )ωx ωz − Jxyωx ωz ; |
|
|
|
|||
dt |
||||
|
y |
|
||
|
dK |
|
= Jzωz + (Jy − Jx )ωx ωy − Jxy (ω2x − ω2y ). (2.15) |
|
|
|
|||
dt |
||||
|
z |
|
С учетом зависимости моментов от параметров движения (1.22), (1.25), (1.28), а также допущения о равенстве нулю моментов крена и рыскания силы тяги, получим следующую систему динамических уравнений собственного вращательного движения самолета относительно его центра масс в проекциях на оси связанной системы координат:
Jx ωx − Jxyωy + (Jz − Jy )ωyωz + Jxyωx ωy
= Mx (β,α,ωx ,ωy ,ρ, V);
Jyωy − Jxyωx + (Jx − Jz )ωx ωz + Jxyωyωz
= Mx (β,α,ωx ,ωy ,ρ, V);
Jzωz + (Jy − Jx )ωx ωy − Jxy (ω2x − ω2y )
= MRz (α,α,β,ωz ,M,ρ, V, pH ,TH ). (2.16)
Продолжим построение математической модели собственного вращательного движения самолета, дополнив систему динамических уравнений (2.16) кинематическими уравнениями. Эти уравнения описывают вращательное движение самолета относительно Земли и позволяют установить зависимость между параметрами положения самолета во вращательном движении относительно Земли (углами крена γ , рыс-
кания ψ , тангажа ϑ ) и параметрами этого движения (скоростями крена ωx , рыскания ωy и тангажа ωz ).G
Вектор угловой скорости самолета ω относительно нормальных
осей равен геометрической сумме угловых скоростей связанной системы координат. Поэтому векторное кинематическое уравнение враща-
тельного движения самолета записывается следующим образом
ωG = γG + ψG + ϑ
Проецируя векторы γG, ψG,ϑ на оси связанной системы координат, получим скалярную систему уравнений:
______________________________________________________________________________________________________________________________
16 май 2003г.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА
ωx = ψsin ϑ+ γ;
ωy = ϑsin γ + ψcos ϑcos γ; (2.18) ωz = ϑcos γ −ψcos ϑsin γ.
Решая систему уравнений (2.18) относительно γ,ψ,ϑ , получим
необходимые кинематические уравнения
γ = ωx − tgϑ(ωy cos γ − ωz sin γ);
ψ = sec ϑ(ωy cos γ −ωz sin γ); (2.19)
ϑ = ωy sin γ + ωz cos γ.
Система динамических уравнений (2.16) и система кинематических уравнений (2.19) представляют собой математическую модель собственного вращательного движения самолета. Таким образом, получены 12 уравнений движения самолета, связывающих между собой 15 параметров положения и движения самолета. Для того, чтобы система уравнений стала замкнутой, и имела решение, необходимы еще три уравнения. Эти уравнения получим, установив геометрические соотношения между углами, определяющими параметры положения и движения самолета.
Пользуясь таблицей направляющих косинусов (табл.1 Приложения) можно путем определенных преобразований получить взаимосвязь между параметрами положения и движения самолета в связанной сис-
теме координат ( γ,ψ,ϑ ), скоростной системе координат ( α,β, γa ) и
траекторной системе координат ( Ψ,θ ). При отсутствии ветра эта связь определяется следующим образом:
sin α ={[sin ϑcos γcos(Ψ −ψ) + sin γsin(Ψ − ψ)]cos θ− sin θcos ϑcos γ}/ cosβ;
sin β = cos θ[sin ϑsin γcos(Ψ − ψ) − - cos γsin(Ψ −ψ)] −sin θcos ϑsin γ;
sin γa = [cos αsin βsin ϑ−
- cos ϑ{sin αsin βcos γ − cosβsin γ}]/ cos θ. (2.20)
Таким образом, математическая модель собственного движения самолета содержит систему динамических (2.10) и систему кинематических (2.11) уравнений поступательного движения, систему динамических (2.16) и систему кинематических (2.19) уравнений вращательного движения, а также систему уравнений геометрических соотношений
(2.20).
Уравнения вынужденного движения. Дополним полученную ма-
тематическую модель собственного движения вынужденной составляющей под действием внешнихG возмущений и управлений. Ветер
изменяет проекции вектора тяги P и вектора аэродинамической силы на оси траекторной системы координат. С учетом зависимостей сил, действующих на самолет от управляющих воздействий и внешних возмущений (1.45), система динамических уравнений поступательного движения самолета (2.10) преобразуется следующим образом:
mV = P(M, pH ,TH ,ρ, V,δP )cos(α −αW ) cos(β−βW ) − Xa (α,M,ρ,V,δx ,fx )
cos αW cosβW + Ya (α, M,ρ,V,δy ,fy ) sin αW sin βW − mgsin θ =
= FxK [α,β,θ, M,V,ρ, pH ,TH , δP ,δx ,δy ,fx ,fy ,αW ,βW ];
mVθ = P(M,pH ,TH ,ρ,V,δP )[sin(α −αW )
cos γa + cos(α − αW )sin(β−βW )sin γa ] + +Xa (α, M,ρ,V,δx ,fx )sin αW sin βW +
+Ya (α, M,ρ,V,δy ,fy )cos γa cos αW cosβW −
−Za (β,ρ, V,δz ,fz )sin γa − mg cos θ =
= FyK [α,β,θ, M,V,ρ, pH ,TH , δP ,δx ,δy ,fx ,fy ,fz ,αW ,βW ];
−mVΨcos θ = P(M,pH ,TH ,ρ, V,δP ) [sin(α −αW )sin γa − cos(α − αW )
sin(β−βW )cos γa ] + Ya (α,M,ρ,V,δy ,fy )
sin γa + Za (β,ρ,V,δz ,fz )cos γa =
= FzK [α,β, γa , M,V,ρ, pH ,TH , δP ,δz ,δy ,fy ,fz ,αW ,βW ] .
(2.21)
С учетом зависимостей моментов, действующих на самолет, от управляющих воздействий и внешних возмущений (1.46) система динамических уравнений вращательного движения самолета (2.16) имеет вид:
Jx ωx − Jxyωy + (Jz − Jy )ωyωz + Jxyωx ωy =
= Mx (β,α,ωx ,ωy ,ρ, V,δЭ,δH , mxв);
Jyωy − Jxyωx + (Jx − Jz )ωx ωz − Jxyωyωz =
= My (β,α,ωx ,ωy ,ρ, V,δЭ,δH , myв);
Jzωz + (Jy − Jx )ωx ωy + Jxy (ω2x − ω2y ) =
= MRz (α,α,β,ωz ,M,ρ, V, pH ,TH ,δP ,δB , mzв) . (2.22)
Система кинематических уравнений поступательного движения (2.11) и система кинематических уравнений вращательного движения (2.19) остаются без изменений. В геометрических соотношениях (2.20) следует учесть составляющие ветра.
sin(α −αW ) ={[sin ϑcos γcos(Ψ −ψ) +
+ sin γsin(Ψ − ψ)]cos θ+sin θcos ϑcos γ} / cos(β−βW );
sin(β−βW ) = cos θ[sin ϑsin γcos(Ψ − ψ) − cos γsin(Ψ −ψ)] −sin θcos ϑsin γ;
sin γ ={cos(α −αW )sin(β−βW )sin ϑ− |
|
- cos ϑ[sin(α −αW )sin(β−βW )cos γ − |
|
- cos(β−βW )sin γ]}/ cos θ. |
(2.23) |
Таким образом, математическая модель вынужденного движения самолета содержит систему динамических (2.21) и систему кинематических (2.11) уравнений поступательного движения, систему динамических (2.22) и систему кинематических (2.19) уравнений вращательного движения, а также систему уравнений геометрических соотношений
(2.23).
2.2. ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
Полученные в предыдущем параграфе математические модели пространственного движения самолета в виде систем дифференциальных уравнений являются нелинейными. Их решение как аналитическими, так и численными методами затруднено. Однако если принять допущение о том, что значения параметров движения самолета в возмущенном движении отклоняются на малые величины по отношению к тем значениям этих параметров, которые имели место до начала действия возмущений, то появляется возможность перейти от нелинейных моделей к линейным моделям.
На этом допущении базируется идея метода малых возмущений, позволяющего рассматривать возмущенное движение самолета как совокупность опорного (невозмущенного) движения и движения под действием малых возмущений.
Примем допущение о малой продолжительности переходных процессов при возникновении возмущений. На этом допущении базируется идея метода "замороженных коэффициентов". Сущность этого метода состоит в том, что отрезок времени t, в течение которого происходит исследуемое движение, разбивается на отдельные интервалы. На этих интервалах коэффициенты уравнений принимаются постоянными и равными их значениям в начале интервала. Тогда математическая модель будет состоять из совокупности дифференциальных уравнений с постоянными коэффициентами, причем число таких уравнений равно числу интервалов времени.
______________________________________________________________________________________________________________________________
15
апрель 2003г.

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ
|
|
Линеаризованные |
уравнения |
собственного |
|
|
поступательного |
|
Аналогичным образом проведем линеаризацию динамического |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
движения. Рассмотрим нелинейную математическую модель собствен- |
уравнения поступательного движения самолета относительно траектор- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ного поступательного движения в виде системы динамических уравне- |
ной оси OY (2.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ний (2.10). Анализ правой части уравнений показывает, что проекции |
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
вектора сил |
G |
|
на оси траекторной системы координат F |
, F |
, F |
mV |
o |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
V |
|
|
|
|
M |
|
|
|
|
|
|
|
θ |
|
|
|
|
|
β |
|
γa |
∆γa |
, |
|||||||||||||||||||||||||||||||||||||||||||||
F |
|
|
∆θ = |
Fyк ∆α + Fyк ∆V |
+ Fyк ∆M + Fyк |
∆θ + Fy |
к |
∆β+ Fy |
к |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xк |
|
yк |
zк |
(2.31) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
являются нелинейными функциями параметров движения самолета и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
V |
M |
|
θ |
|
||||||||||||||||||||||||||||||||||||||||||||||
параметров окружающей среды. |
Пренебрегая изменением с высотой |
|
где |
|
|
|
значения |
|
коэффициентов |
|
|
уравнения |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плотности воздуха ρH , давления |
pH и температуры TH с достаточ- |
|
|
|
|
|
|
|
|
Fyк |
, Fyк , Fyк |
,Fyк , |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fβ , Fγa |
|
приведены в таблице П2 Приложения. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ной для практики точностью приближения |
эти функции можно пред- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ставить следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yк |
|
|
yк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для динамического уравнения поступательного движения самолета |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fxк |
= Fxк (α,β,θ,M, V); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно траекторной оси OZк |
(2.10) получим следующее линеа- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fyк |
= Fyк (α,β,θ, γa ,M, V); |
(2.24) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ризованное уравнение |
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
F |
|
|
= F |
(α,β, γ |
|
|
,M, V). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−mV |
o |
cos θ |
o |
|
|
|
|
|
|
α |
|
|
|
|
|
∆V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆Ψ = Fz |
к |
∆α + Fz |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
zк |
|
|
|
zк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.32) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Применим метод малых возмущений для линеаризации уравнений |
|
|
+F |
M |
|
|
|
|
|
|
|
θ |
|
|
|
|
|
β |
∆β + F |
γa |
∆γ |
|
, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2.10) с учетом зависимостей (2.24). Параметры возмущенного движе- |
|
|
|
|
|
∆M + F |
|
∆θ+ F |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
zк |
|
|
|
|
|
|
|
|
zк |
|
|
|
|
|
zк |
|
|
|
|
zк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ния |
|
|
|
выражаются |
|
|
|
через |
|
параметры |
|
|
|
|
опорного |
|
|
движения |
|
Значения |
|
коэффициентов |
уравнения |
|
|
α |
, F |
V |
,F |
M |
θ |
β |
, F |
γa |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
o |
|
|
o |
|
|
o |
|
|
o |
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
,F |
,F |
|
|
|||||||||||||||||||||||||||||||||||||||
α |
,β |
,θ |
|
|
,M |
, V |
и малые отклонения параметров возмущен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zк |
zк |
|
zк |
zк |
zк |
|
zк |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
, γa |
|
|
приведены в табл.П2 приложения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ного |
|
|
движения |
|
от |
|
их |
|
значений |
в |
|
|
|
опорном |
|
|
движении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
∆α, ∆β, ∆θ, ∆γa , ∆M, ∆V : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линеаризуем кинематические уравнения поступательного движе- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния самолета (2.11). Для опорного движения вдоль траекторной оси |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
α = αo + ∆α; β = βo + ∆β; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OXк : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
θ = θo + ∆θ; |
γa |
= γao + ∆γa ; |
(2.25) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dLo |
|
= Vo cos θo cos Ψo . (2.33) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
M = Mo + ∆M; V = Vo + ∆V. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для возмущенного движения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
Рассмотрим первое из динамических уравнений (2.10) поступа- |
|
|
d |
(Lo + ∆L) = Vo cos |
θo cos Ψo + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тельного движения самолета относительно траекторной оси OXк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
m |
dV |
= Fxк (α,β,θ,M, V). (2.26) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
(V cosθcos Ψ)o ∆V + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Опорному движению соответствует одно из частных решений |
|
|
+ |
|
|
d |
|
(Vo cosθcos Ψ)o |
∆θ + |
|
d |
|
(V cosθcos Ψ)o ∆Ψ. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнения (2.26) |
V = Vo . Если подставить это частное решение в |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dθ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2.26), то получим уравнение, отвечающее опорному движению: |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dΨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dVo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычтем из уравнения (2.34) уравнение (2.33): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
m |
|
= F |
(αo ,βo ,θo ,Mo , Vo ). (2.27) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆L = cos θo cos Ψo∆V − Vo cos Ψo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
xк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.35) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Вычтем из уравнения (2.26) уравнение (2.27) |
|
|
|
|
|
|
|
|
|
|
|
|
sin θo∆θ− Vo cosθo sin Ψo∆Ψ. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dV |
= Fxк (α,β,θ,M, V) − Fxк (α |
o |
,β |
o |
,θ |
o |
|
|
o |
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Аналогичным образом выполним преобразования для двух других |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
m |
|
dt |
|
|
|
, M |
|
,V |
|
). (2.28) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
уравнений (2.11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Разложим нелинейную функцию F |
|
|
(α,β,θ, M,V) |
в ряд Тейло- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
∆V + V |
o |
cos θ |
o |
∆θ |
o |
, |
|
|
|
|
|
|
|
|
|
|
|
|
(2.36) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆H = sin θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ра по степеням вариаций |
∆α, ∆β, ∆θ, ∆M, ∆V |
в окрестности значе- |
|
|
∆ |
|
|
|
= |
|
V |
o |
sin |
θo |
sin |
Ψo∆θ − |
cos |
θo |
sin |
Ψo∆ |
V |
− |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.37) |
|
|
|
|
|||||||||||||||||
ний αo ,βo ,θo , Mo ,Vo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−Vo cosθo cos Ψo∆Ψ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
F |
|
(α,β,θ, M,V) = F |
(αo ,βo ,θo ,Mo ,Vo ) + |
|
|
|
|
|
|
|
|
|
|
Линеаризованные |
уравнения |
|
|
собственного |
|
вращательного |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
движения. Нелинейная математическая модель собственного враща- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
α |
|
|
|
|
|
|
β |
|
|
|
|
|
θ |
|
|
M |
|
|
|
|
V |
∆V + |
|
|
|
|
|
|
|
|
тельного движения самолета содержит систему динамических уравне- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+Fxк ∆α + Fxк |
∆β + Fxк |
∆θ+ Fxк ∆M |
+ Fxк |
|
(2.29) |
|
|
|
ний (2.16) и систему кинематических уравнений (2.19). Анализ правой |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+Fxк (∆α, ∆β, ∆θ, ∆M, ∆V), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
части динамических уравнений показывает, что проекции вектора ре- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зультирующего момента |
MR на оси связанной системы координат |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂Fxк |
|
|
|
|
|
∂Fxк |
|
|
|
|
|
|
|
|
|
∂Fxк |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
α |
= |
|
β |
= |
|
|
|
|
θ |
|
= |
|
|
|
M |
|
,M |
|
|
, M |
|
|
|
являются нелинейными функциями параметров дви- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Fx |
|
|
|
|
|
|
|
|
, Fx |
|
|
|
|
|
|
|
|
,Fx |
|
|
|
|
|
|
|
, |
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
R Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
к |
∂α |
к |
|
|
∂β |
|
к |
∂θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
где |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
жения |
|
|
самолета и управляющих воздействий. Эти функции с достаточ- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂Fxк |
|
|
|
|
|
|
∂Fxк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной для практических задач точностью можно представить следующим |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
FM = |
|
,FV |
= |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
к |
|
∂M |
|
x |
к |
|
∂V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mx = Mx (α,V,ωx ,ωy ,β); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
- частные производные, взятые в окрестности опорного движения |
|
|
My = My (α, V,ωx ,ωy ,β); |
|
|
|
|
(2.38) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
значения |
|
которых |
|
определены |
в |
табл.П2. |
с |
|
учетом (1.13); |
|
|
MRZ |
|
= MRZ (α,α,ωz ,V,M,β). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F |
|
(∆α, ∆β, ∆θ, ∆M, ∆V) - совокупность членов разложения выше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим |
|
|
параметры |
возмущенного |
движения |
через |
параметры |
|
||||||||||||||||||||||||||||||||||||||||||
первого порядка малости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωox ,ωoy ,ωoz ,α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
Подставим разложение (2.29) в уравнение (2.28) и получим линей- |
опорного |
|
|
|
движения |
|
|
|
и |
|
малые |
отклонения |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ное динамическое уравнение поступательного движения самолета от- |
∆ωx , ∆ωy , ∆ωz , ∆α : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
носительно траекторной оси OXк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
V |
|
|
|
|
M |
|
|
|
|
|
θ |
|
|
|
|
|
β |
∆β. (2.30) |
|
|
ω |
x |
|
= ωo |
+ ∆ω |
x |
; ω |
y |
|
= ωo |
|
+ ∆ω |
y |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
m∆V |
= Fxк |
∆α + Fxк ∆V |
+ Fxк ∆M + Fxк ∆θ + Fxк |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
ωz = ωoz + ∆ωz ; α = α0 + ∆α.
______________________________________________________________________________________________________________________________
18 май 2003г.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА
|
|
Рассмотрим первое из динамических уравнений (2.16) вращатель- |
Аналогичным образом выполняю линеаризацию кинематических |
||||||||||||||||||||||||||||||||||||||||||
ного движения относительно оси |
OX . Опорному движению соответ- |
уравнений вращательного движения (2.19), для которых, пренебрегая |
|||||||||||||||||||||||||||||||||||||||||||
ствует одно из частных решений уравнения (2.16) для ω |
|
= ωo и |
величинами второго порядка малости, получим: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
∆γ = (ωoz sin γo − ωoy cos γo )∆ϑ / cos2 ϑo |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
ω |
|
= ωo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
||||||||||||||||||||
y |
. Если подставить это частное решение в (2.16), то получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.44) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ωo |
− tgϑo cos γo∆ω |
y |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнение, отвечающее опорному движению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
∆ϑ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
dωo |
|
|
dωoy |
|
|
|
|
|
|
|
|
)ωo |
ωo |
|
|
|
= cos γo∆ωz + sin γo∆ωy + (ωoy cos γo − ωoz sin γo )∆γ; |
||||||||||||||||||||||
|
|
J |
|
|
|
x |
− J |
|
|
|
|
|
+ (J |
|
− J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dt |
xy dt |
|
|
|
(2.39) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.45) |
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
z |
|
|
y |
y |
z |
|
|
∆ψ |
= −sin γo∆ωz / cos ϑo + ωoy cos γo tgυo∆ϑ / cos ϑo + |
||||||||||||||||||||||||||
|
|
+Jxyωoxωoy = Mx (αo ,Vo ,ωox ,ωoy ,βo ). |
|
|
|
(2.46) |
|||||||||||||||||||||||||||||||||||||||
|
|
В ближайшей окрестности опорного движения: |
|
|
cos γo∆ωy / cos ϑo − (ωoy sin γo + ωoz cos γo )∆γ / cos ϑo . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
d |
|
o |
|
|
|
|
|
|
|
|
|
d |
|
|
o |
|
|
|
|
Линеаризованные геометрические соотношения между углами, оп- |
|||||||||||||||||||
|
|
Jx |
|
(ωx − ∆ωx ) |
− Jxy |
|
(ωy − ∆ωy ) + |
|
|
ределяющими положение самолета в различных системах координат |
|||||||||||||||||||||||||||||||||||
|
|
dt |
dt |
|
|
||||||||||||||||||||||||||||||||||||||||
(Jz − Jy )(ωoy + ∆ωy )(ωoz + ∆ωz ) |
|
|
|
|
(2.20), с учетом пренебрежения величинами второго порядка малости |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
принимают вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
+Jxy (ωox + ∆ωx )(ωoy + ∆ωy ) |
|
|
|
|
|
|
|
|
|
|
cos γo cosθo |
|
|
|
o |
|
|
|
o |
|
|
|
o |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
∆α = cos αo cosβo [cos ϑ |
|
cos(Ψ |
|
− ψ |
|
) |
(2.47) |
|
|||||||||||||||||||||||||||||
= Mx (αo , Vo ,ωox ,ωoy ,βo ) + Mαx ∆α |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∆ϑ − cos ϑo∆θ+ sin(Ψo − ψo )∆γ]. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
+MVx ∆V + Mωx x ∆ωx + Mωx y ∆ωy + Mβx ∆β (2.40) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
∆ψ = tgγo cos ϑo∆υ |
− |
tgγo cos ϑo |
|
∆θ |
|
|
||||||||||||||||||||||||||||||||||||
+M |
|
|
(∆α, ∆V, ∆ω |
|
, ∆ω |
|
, ∆β), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x |
x |
y |
|
|
|
|
|
|
|
cos(Ψ |
o |
− ψ |
o |
) |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
− cosβo∆β
где cos θo cos γo cos(Ψo − ψo )
|
∂M |
|
|
= Mαx |
|
∂M |
|
|
|
|
= MVx ; |
|
∂M |
|
= Mωx x ; |
|
|
x |
|
; |
|
x |
|
|
|
|
x |
||||
|
∂α |
0 |
|
|
∂V |
0 |
|
|
∂ωx 0 |
|
|||||
|
∂M |
x |
|
ω |
|
∂M |
x |
|
|
= Mβx , |
|
|
|
|
|
|
|
|
= Mx y ; |
|
|
|
|
|
|
|
|
||||
|
∂ωy |
|
|
|
∂β |
|
0 |
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
- производные, значения которых взяты в окрестности опорного движения с учетом (1.23) и приведены в приложении табл. П3 приложения;
Mx (∆α, ∆V, ∆ωx , ∆ωy , ∆β) - совокупность членов разложения
выше первого порядка малости.
Вычтем из уравнения (2.40) уравнение (2.39) и получим линейное динамическое уравнение вращательного движения самолета относи-
тельно связанной оси OX
Jx ∆ωx − Jxy∆ωy = Mαx ∆α + MVx ∆V +
(2.41)
Mωx x ∆ωx + Mωx y ∆ωy + Mβx ∆β.
+[sin ϑo − tgθo cos(Ψo − ψ o )]∆γ; (2.48) ∆γa = cos γa1cosθo [− cos ϑo cosαo sin βo
cos γo∆α + cosαo cos ϑo sin βo∆ϑ + cosβo (2.49) (cosαo sin ϑo − cos ϑo cos γo sin αo )∆β +
cos ϑo cosβo cos γo∆γ].
Таким образом, линеаризованная математическая модель собственного движения самолета характеризуется уравнениями (2.30) (2.32), (2.35) - (2.37), (2.41) -(2.49).
Линеаризованные уравнения полного вынужденного простран-
ственного движения. Проведем линеаризацию математической модели вынужденного движения самолета (2.21) с учетом того, что проекции
вектора сил Fк на оси траекторной системы координат следующим
Аналогичным способом проведем линеаризацию динамического |
образом зависят от параметров управляющих и возмущающих воздей- |
уравнения вращательного движения самолета (2.16) относительно свя- |
ствий: |
занной оси OY :
Jy∆ωy − Jxy∆ωx = Mαy ∆α + MVy ∆V +
(2.42)
Mωy x ∆ωx + Mωy y ∆ωy + Mβy∆β,
где |
значения |
коэффициентов |
уравнения |
Mαy , MVy ,Mωy x ,Mωy y , Mβy взяты в окрестности опорного движения и
приведены в табл.П3 приложения.
Для динамического уравнения вращательного движения самолета относительно связанной оси OZ (2.16) получим следующее линеари-
зованное уравнение: |
|
|
|
|
|
|
|
|
|
||||
J |
∆ω |
я |
= MωZ ∆ω |
z |
+ Mα ∆α + Mα |
∆α |
+ |
|
|
|
|||
z |
|
|
RZ |
|
RZ |
RZ |
|
(2.43) |
|
|
|
||
+MV |
|
∆V + MM |
∆M + Mβ |
∆β, |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
Rz |
RZ |
|
|
RZ |
|
|
|
|
|
|
|
где |
значения коэффициентов |
уравнения |
MωZ ,Mα |
,Mα |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
RZ |
RZ |
RZ |
|
MVRz , MMRZ ,MβRZ взяты в окрестности опорного движения и приве-
дены в табл.П3 приложения.
Fxк = Fxк (δx ,δy ,δP ,fx ,fy ,αW ,βW );
Fyк = Fyк (δx ,δy ,δz ,fx ,fy ,fz ,αW ,βW ); (2.50) Fzк = Fzк (δy ,δz ,δP ,fy ,fz ,αW ,βW ).
Тогда для динамического уравнения поступательного движения относительно оси OXк с учетом уравнения собственного движения
(2.30) получим
m∆V = Fxαк ∆α + FxVк ∆V + FxMк ∆M + Fxθк ∆θ
|
β |
|
|
δ |
|
|
|
+ F |
δy |
∆δ |
|
δ |
∆δ |
|
|
+ |
(2.51) |
|
|
|
|
||||
+F |
∆β+ F x ∆δ |
x |
|
y |
+ F P |
P |
|
|
|
|
|
||||||||||||||
|
xк |
|
|
xк |
|
|
|
xк |
|
|
xк |
|
|
|
|
|
|
|
|
|
|||||
f |
∆f |
|
fy |
∆f |
|
+ F |
α |
W ∆α |
|
|
β |
|
|
|
|
, |
|
|
|
|
|
||||
F x |
x |
+ F |
y |
|
W |
+ F W ∆β |
W |
|
|
|
|
|
|||||||||||||
xк |
|
|
xк |
|
|
xк |
|
|
xк |
|
|
|
|
|
|
|
|
||||||||
где |
|
|
коэффициенты |
|
|
уравнения |
|
δ |
|
δy |
δ |
f |
,F |
fy |
, |
||||||||||
|
|
|
|
F |
|
x ,F |
, F P , F x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xк |
xк |
xк |
xк |
xк |
|
|||
FαW , FβW приведены в табл.П4 приложения. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
xк |
xк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Динамическое уравнение поступательного движения относительно траекторной оси OYк с учетом уравнения собственного движения (2.32) имеет вид:
______________________________________________________________________________________________________________________________
15
апрель 2003г.

В.Г.Воробьев, С.В.Кузнецов АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ПОЛЕТОМ САМОЛЕТОВ
mV |
o |
|
α |
∆α + F |
V |
∆V |
+ F |
M |
|
|
|
θ |
∆θ |
+ |
|
|
||||||||||||||||
|
∆θ |
= F |
|
|
|
|
∆M + F |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
yк |
|
|
|
|
yк |
|
|
|
|
yк |
|
|
|
yк |
|
|
|
|
|
||||||
β |
|
|
|
|
δ |
|
|
|
|
|
δy |
∆δ |
|
|
|
δ |
|
|
|
δ |
|
∆δ |
|
+ (2.52) |
|
|||||||
F |
|
|
∆β + F x ∆δ |
x |
+ F |
|
y |
+ F z δ |
z |
+ F P |
P |
|
||||||||||||||||||||
yк |
|
|
|
|
zк |
|
|
|
|
zк |
|
|
|
|
|
zк |
|
|
zк |
|
|
|
|
|
|
|||||||
|
|
|
f |
x |
∆f |
|
+ F |
fy |
∆f |
|
+ F |
α |
W ∆α |
|
|
|
β |
|
|
|
, |
|
|
|
|
|||||||
+F |
x |
|
|
y |
|
|
W |
+ F |
W ∆β |
W |
|
|
|
|
||||||||||||||||||
|
|
|
zк |
|
zк |
|
|
|
|
zк |
|
|
|
|
|
zк |
|
|
|
|
|
|
||||||||||
где |
|
|
|
коэффициенты |
|
|
|
|
|
уравнения |
|
|
|
δ |
|
δy |
δ |
δ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
F x , F |
,F z |
,F P , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zк |
|
zк |
zк |
zк |
f |
|
fy |
|
α |
β |
|
|
|
приведены в табл.П4. приложения. |
|
|
|||||||||||||||||||||
F x ,F |
|
|
,F |
W ,F W |
|
|
|
|
||||||||||||||||||||||||
zк |
zк |
|
zк |
zк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для динамического уравнения поступательного движения относительно траекторной оси OZк с учетом уравнения собственного дви-
жения (2.32) имеет вид
−mVo cos θo∆Ψ = Fzαк ∆α + FzVк ∆V +
|
F |
M |
∆M |
|
|
θ |
∆θ |
|
β |
∆β |
|
|
δx |
∆δ |
|
+ |
|
|
|
|
|||||||||
|
|
|
+ F |
+ F |
|
+ F |
|
x |
|
|
|
|
|||||||||||||||||
|
zк |
|
|
|
|
|
zк |
|
|
|
zк |
|
|
|
zк |
|
|
|
(2.53) |
|
|
|
|||||||
|
|
δy |
|
|
|
|
|
|
δ |
|
|
|
|
δ |
|
|
|
|
f |
|
|
|
|
|
|
||||
|
F |
∆δ |
|
|
|
|
|
|
|
|
|
|
|
x ∆f |
|
+ |
|
|
|
||||||||||
|
|
|
y |
|
+ F z δ |
z |
+ F |
P ∆δ |
P |
+ F |
x |
|
|
|
|||||||||||||||
|
zк |
|
|
|
|
|
zк |
|
|
|
zк |
|
|
|
zк |
|
|
|
|
|
|||||||||
|
F |
fy |
∆f |
|
|
+ F |
α |
W |
∆α |
|
|
β |
|
|
|
|
|
, |
|
|
|
|
|
|
|||||
|
|
|
y |
|
W |
+ F W ∆β |
W |
|
|
|
|
|
|
||||||||||||||||
|
zк |
|
|
|
zк |
|
|
|
|
zк |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
где |
|
|
|
|
коэффициенты |
|
|
уравнения |
δ |
δy |
δ |
δ |
||||||||||||||||
|
|
|
|
|
|
|
F x , F |
,F z |
, F P , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zK |
zK |
zK |
zK |
f |
,F |
fy |
|
|
α |
|
|
β |
|
|
|
|
|
|
|
|
в |
табл.П4 |
приложения. |
Уравнения |
|||||||||
F x |
|
|
, F |
|
W , F W приведены |
|
|||||||||||||||||||||||
zK |
|
zK |
|
|
zK |
zK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(2.35) - (2.37) остаются без изменений. Для динамических уравнений вращательного движения учтем следующие зависимости проекций
вектора результирующего момента MR от управляющих и возмущающих воздействий:
Mx = Mx (δэ,δн, mxв,αW ,βW );
My = My (δэ,δн,myв,αW ,βW ); (2.54)
MR z = MRz (δв,δP ,ϕ, mzв,αW ,βW ).
Тогда для динамического уравнения вращательного движения от-
носительно оси OX с учетом уравнения собственного движения (2.41) получим
Jx ∆ωx − Jxy∆ωy = Mαx ∆α + MVx ∆V + |
|
Mωx x ∆ωx + Mωx y ∆ωy + Mβx ∆β+ Mδxэ ∆δэ + |
(2.55) |
Mδxн ∆δн + Mmx xв ∆mxв + Mαx W ∆αW + MβxW ∆βW , |
|
где коэффициенты уравнения Mδxэ , Mδxн ,Mmx xв , |
Mαx W ,MβxW |
приведены в табл.П5. приложения.
Динамическое уравнение вращательного движения относительно оси OY с учетом уравнения собственного движения (2.42) имеет вид:
Jy∆ωx − Jxy∆ωy = Mαy ∆α + MVy ∆V + |
|
|
|
|||
Mωy x ∆ωx + Mωy y ∆ωy + Mβy∆β+ Mδyэ ∆δэ + |
|
(2.56) |
||||
δ |
myв |
α |
|
β |
|
|
Myн ∆δн + My |
∆myв + My W ∆αW + MyW ∆βW , |
|||||
|
|
δ |
δ |
myв |
, |
α β |
где коэффициенты уравнения Myэ , Myн ,My |
My W ,MyW |
|||||
приведены в табл.П5 приложения.
Для динамического уравнения вращательного движения относи-
тельно |
|
оси OZ с |
учетом уравнения собственного движения (2.43) |
|||||||
получим |
|
|
|
|
|
|
|
|
||
|
|
|
ωZ |
α |
. . |
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
||
Jz ∆ωz = MRZ ∆ωz + MRZ ∆α + MRZ ∆α+ |
|
|
|
|
||||||
+MV |
|
∆V + MM |
∆M + Mβ ∆β + Mδв ∆δ |
в |
+ |
|
|
|
||
RZ |
|
RZ |
RZ |
RZ |
|
|
|
|
||
ϕ |
|
|
δP |
mzв |
αW |
|
|
βW |
|
|
+MRZ |
∆ϕ + My ∆δP + MRZ |
∆mzв + MRZ |
∆αW + MRZ ∆βW , |
|
||||||
(2.57) |
|
|
|
|
|
|
|
|
|
|
где |
|
коэффициенты |
уравнения |
|
δв |
ϕ |
δP |
, |
||
|
|
MRz |
, MRz |
, MRz |
||||||
mzв |
|
αW |
βW |
приведены в табл.П5 приложения. |
|
|
|
|||
MRz |
,MRz |
, MRz |
|
|
|
|||||
Система линеаризованных кинематических уравнений вращательного движения самолета (2.44) - (2.46) остается без изменений.
В линеаризованных геометрических соотношениях учтем составляющие ветра:
∆α = ∆αW + |
cos γo cos θo |
|
[cos ϑo cos(Ψo − ψo ) − cos ϑo∆θ+ |
|||||||
cosαo cosβo |
|
|||||||||
|
|
|
|
|
|
|
||||
+ sin(Ψo − ψo )∆γ]; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
tgγo cos ϑo |
(2.58) |
|||
∆ψ = tgγo cos ϑo∆ϑ − |
|
∆θ |
||||||||
cos(Ψo − ψo ) |
||||||||||
|
|
|
|
|
|
|||||
|
cosβo (∆β− ∆βW ) |
|
||||||||
− |
|
|
+ |
(2.59) |
||||||
cos θo cos γo cos(Ψo − ψo ) |
||||||||||
+[sin ϑo − tgθo |
|
cos |
ϑo |
|
||||||
|
|
|
|
|
]∆γ. |
|
||||
|
|
|
|
|
|
|||||
|
|
|
cos(Ψo − ψo ) |
|
||||||
Таким образом, линеаризованная математическая модель вынужденного движения самолета содержит уравнения (2.51) -(2.53), (2.55) - (2.59), (2.35) - (2.37), (2.44) - (2.46).
2.3. УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА В ФОРМЕ КОШИ
Линеаризованная математическая модель отражает физику полного собственного пространственного движения самолета. Однако ее практическое использование затруднено, так как аналитическое решение системы дифференциальных уравнений такой высокой размерности сопряжено с известными сложностями. Для того, чтобы систему уравнений можно было решать с помощью ЭВМ, ее удобно представить в форме Коши, когда в левой части системы уравнений содержатся только первые производные от переменных, а в правой части - линейные комбинации переменных.
Уравнения собственного поступательного движения в форме Коши. Преобразуем уравнения собственного поступательного движения к форме Коши. Поделим в уравнении (2.30) левую и правую части на массу самолета m, а вместо приращения угла наклона траектории
∆θ подставим его значение из уравнения (2.47). Тогда уравнение относительно скорости ∆V принимает вид:
|
|
|
|
∆V = aV,α∆α + aV,ϑ∆ϑ + aV,V ∆V + aV,β∆β + aV,γ ∆γ. (2.60) |
|||
Обозначения |
для |
коэффициентов |
уравнения |
aV,α ,aV,ϑ ,aV,V ,aV,β,aV,γ |
приведены в табл.П6 приложения. |
||
Левую и правую части уравнения (2.31) поделим на произведение
массы самолета на скорость в опорном движении mVo .
Кроме того, подставим вместо приращения скоростного угла крена ∆γa его значение из уравнения (2.49):
∆θ = aθ,α∆α + aθ,V ∆V + aθ,θ∆θ+ aθ,ϑ∆ϑ + aθ,β∆β + aθ,γ ∆γ .
(2.61) |
|
|
|
Обозначения |
для |
коэффициентов |
уравнения |
aθ,α ,aθ,V ,aθ,θ,aθ,ϑ ,aθ,β,aθ,γ |
приведены в табл.П6. |
|
|
Левую и |
правую части |
уравнения (2.32) |
поделим на |
−mVo cosθo . Подставим вместо приращения скоростного угла креего значение из уравнения (2.49):
aΨ,α∆α + aΨ,ϑ∆ϑ + aΨ,V∆V + aΨ,β∆β + aΨ,γ ∆γ . (2.62)
Обозначения для коэффициентов уравнения aΨ,α ,aΨ,ϑ ,aΨ,V ,aΨ,β,aΨ,γ приведены в табл.П6.
В кинематических уравнениях поступательного движения (2.35) и (2.37) введем обозначения aL,V ,aL,ϑ ,aL,Ψ,az,V ,az,θ,az,Ψ согласно табл.П7 приложения:
∆L = aL,V ∆V + aL,θ∆θ+ aL,Ψ∆Ψ; (2.63) ∆z = az,V ∆V + az,θ∆θ + az,Ψ∆Ψ. (2.64)
В кинематическом уравнении (2.36) заменим приращение угла наклона траектории ∆θ его значением из уравнения (2.47). Тогда с уче-
______________________________________________________________________________________________________________________________
20 май 2003г.
