
UP_nadezhnost_i_diagnostika
.Pdf
|
ЗАКАЗ |
ПРОДУКТ |
ПОЛУЧАТЕЛЬ |
ПРОИЗВОДИТЕЛЬ |
|
|
|
|
|
Атрибуты |
Код |
Код продукта |
Код получателя |
Код производителя |
|
покупателя |
Дата |
Дата |
Код продукта |
|
Код продукта |
Остаток |
Состояние р/с |
Дата |
|
Дата |
|
|
Наличие |
|
составления |
|
|
|
|
Заказ. |
|
|
|
|
Количество |
|
|
|
Методы |
Оформить |
Выдать |
Перечислить с |
Отгрузить |
|
Отложить |
остаток |
р/с |
|
|
Выполнить |
Изменить |
|
|
|
Оплатить |
остаток |
|
|
|
Создать |
|
|
|
|
Уничтожить |
|
|
|
Приложение 3. Основы нечеткого анализа
Теория нечетких множеств представляет собой сложившееся научное направление, поток публикаций по которому не иссякает. Факт появления этой теории ее основоположник (выходец из Советского Союза) – Лотфи Заде – прокомментировал следующим образом [12]:
«Теория нечетких множеств – это, по сути дела, шаг на пути к сближению точности классической математики и всепроникающей неточности реального мира, к сближению, порожденному непрекращающимся человеческим стремлением к лучшему пониманию процессов мышления и познания».
Нечеткие методы находят применение в различных прикладных областях. Среди них:
Психология.
Физиология.
Политические науки.
Физиология.
Экономика.
Наука об управлении (принятие решений, формирование оценок и управления).
И т.д.
Однако, обобщая известные приложения, приближенно можно считать, что наибольшую значимость они имеют в задачах принятия решений и управления. При этом можно следующим образом конкретизировать ситуации, когда эти методы применять наиболее целесообразно:
1.Недостаточность или неопределенность знаний о системе, а получение требуемой информации является сложной, дорогостоящей или даже невозможной задачей.
2.Высокая сложность четких моделей.
3.Значимая часть информации о системе доступна в виде экспертных данных.
4.Неясность или нечеткость описания состояний системы.
131
5.Традиционные методы не могут осуществить адекватную обработку неопределенной информации.
6.Нелинейность реальных систем.
Рассмотрим два характерных примера применения нечеткого подхода, на которых в дальнейшем мы остановимся более подробно. Первый пример посвящен синтезу управления для кондиционера. Он соответствует ситуации, представленной в п. 3 предыдущего списка, а именно, алгоритм управления задан в виде словесного (лингвистического) описания. Необходимо определить его реализацию.
Второй пример связан с п.п. 1 и 2 списка ситуаций, когда на практике зачастую затруднительно или даже невозможно получить для сложной нелинейной системы строгую математическую модель. Для этих случаев в 1985 г. Такаги и Сугено предложили нечеткую композиционную модель, по сути представляющую собой особую линеаризацию сложной нелинейной системы, когда её модель представляется множеством нечетко связанных простых линейных моделей. При этом выделяется набор переменных, от которых нелинейно зависит какая-либо функция системы и значения которых могут быть измерены. Область значений этих переменных разбивается на нечеткие («пересекающиеся») интервалы. Каждому интервалу сопоставляется линейная модель. Для каждой из этих моделей известными методами синтезируется свой наблюдатель и свой контроллер. Далее результирующая оценка состояния системы формируется в виде взвешенной суммы частных оценок, получаемых наблюдателями из банка наблюдателей, а результирующее управление – в виде взвешенной суммы частных управлений, формируемых контроллерами из банка контроллеров.
Обсудим, не претендуя на исчерпывающее изложение, некоторые положения теории нечетких множеств. Считая, что знания аудитории в области теории вероятностей более основательны, нежели в теории нечетких множеств и что существуют определенные аналогии между этими направлениями, будем стараться в процессе обсуждения проводить параллели между этими двумя теориями. Для начала отметим, что в теории вероятностей обсуждение ведется на языке частот (вероятностей) событий, в теории нечетких множеств – на языке степеней обладания (степеней принадлежности) некоторыми свойствами элементами из заданного множества. Если теория вероятностей отвечает на вопрос: «Какова частота (вероятность) того или иного события?», то теория нечетких множеств отвечает на вопрос: «В какой степени рассматриваемое свойство присуще некоторому элементу множества?» (какова степень принадлежности рассматриваемого элемента к множеству элементов с определенным свойством?). Эти теории используются в одних и тех же прикладных областях и даже подчас в рамках одних и тех же задач, но отвечают при этом на разные вопросы. Так в задаче о цветных шарах, извлекаемых из урны, теория вероятностей может ответить на вопрос: «Какова вероятность
132
извлечения красного шара?», а теория нечетких множеств – на вопрос: «В какой степени извлеченный шар может быть отнесен к числу красных?».
Два последних критерия прокомментирует несколько позже. Теперь перейдем к формальным определениям [17].
В традиционной прикладной математике множество понимается как
совокупность элементов, обладающих некоторым общим свойством. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Понятие нечеткого множества – |
||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
это |
вариант |
|
математической |
||||||||
|
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формализации |
|
|
|
нечеткой |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
информации. В основе этого понятия |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лежит представление о том, что |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляющие |
данное |
множество |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элементы, |
|
обладающие |
общим |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
-0.5 |
|
|
|
0 |
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
свойством, |
|
могут |
обладать |
этим |
||||||
|
|
Рис.П3.1. Нечеткое множество |
|
|
свойством |
в |
различной |
степени и, |
|||||||||||||||||||||||||
|
|
вещественных чисел, близких к нулю. |
|
|
следовательно, |
|
принадлежать |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данному |
множеству |
с |
разной |
|||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
степенью. |
Пусть |
X |
- |
обычное |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множество элементов. |
|
|
|
|||||
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение П3.1. |
|
Нечетким |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x (м) |
множеством |
C |
в |
X называется |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совокупность пар вида ( x, C ( x)) , где |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x X , а |
C |
- функция, заданная на |
||||||
|
|
0 |
|
1.0 |
|
|
2.0 |
3.0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
множестве |
|
X |
и |
принимающая |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Рис.П3.2. Нечеткое множество высоких |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
значения из |
интервала |
[0,1], |
т.е. |
||||||||||||||||||||||||||
|
|
мужчин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C : X [0, 1] . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Функция C называется функцией принадлежности |
|
нечеткого |
|||||||||||||||||||||||||||||
множества |
C . |
Значение |
|
этой функции для |
конкретного |
x |
называется |
||||||||||||||||||||||||||
степенью принадлежности этого элемента нечеткому множеству C . |
|
|
|||||||||||||||||||||||||||||||
|
|
Обычно функция |
C |
назначается экспертом. |
То, что любое нечеткое |
||||||||||||||||||||||||||||
множество |
C |
всегда |
является |
подмножеством |
некоторого |
|
обычного |
||||||||||||||||||||||||||
множества |
X , послужило причиной тому, что в англоязычной литературе |
||||||||||||||||||||||||||||||||
нечеткое множество зачастую называют нечетким подмножеством. Тем не менее, ниже будет использоваться термин «нечеткое множество». ЕслиC ( x) =1 для любого x X , то C - обычное множество, совпадающее с X .
Рассмотрим примеры нечетких множеств.
Пример. Рассмотрим обычное конечное множество X :
X ={a, b, c, d, e, f}.
Зададим на нем нечеткое множество:
C ={(a | 0), (b | 1), (c | 0.5), (d | 0), (e | 0.5), (f | 0)}.
Пример. Пусть N – множество натуральных чисел. Определим нечеткое множество C «небольших» натуральных чисел:
C ={(0 | 1), (1 | 0.8), (2 | 0.6), (3 | 0.4), …}.
133
Иногда усматривается сходство между функцией принадлежности и вероятностью. Это сходство в значительной степени внешнее и ограничивается общностью области значений. Действительно, невозможно трактовать как вероятность степень принадлежности, например, конкретного человека с ростом 180 см к группе высоких людей, т.к. факт принадлежности не является случайным событием. Как следствие, нет необходимости в условии нормировки для значений функции принадлежности (в теории вероятностей для событий, образующих полную группу, сумма вероятностей должна быть равна единице).
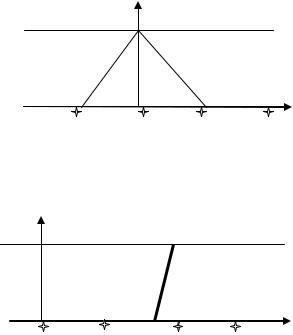
Нечеткое множество может быть описано графически в виде графика функции принадлежности. На рис.П3.1 приведено нечеткое множество вещественных чисел, близких к нулю, а на рис.П3.2 нечеткое множество высоких мужчин.
Вид функции принадлежности отражает мнение эксперта, ее назначающего, и, конечно же, контекст, в котором она используется. Так, например, в обыденной жизни мужчина ростом 1.8 м будет признан высоким, а среди баскетболистов будет числиться «малышом».
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности.
В теории нечетких множеств вводятся аналоги традиционных теоретико-
множественных операций включения, объединения и пересечения. |
|
|||
Определение 2. Пусть A и |
B - нечеткие множества в |
X , а A (x) |
и |
|
B (x) - их функции принадлежности соответственно, то говорят, что |
A |
|||
включает в себя |
B (B A) , |
если для любого x X |
выполняется |
|
неравенство B (x) |
A (x) . |
|
|
|
Определение 3. Объединением нечетких множеств A и B в X называется нечеткое множество A B с функцией принадлежности вида
A B (x) max A (x), B (x) , x X .
Определение 4. Пересечением нечетких множеств A и B в X
называется нечеткое множество A B с функцией принадлежности вида |
|
A B (x) min A (x), B (x) , |
x X . |
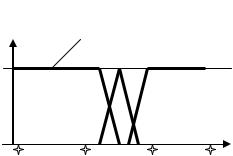
С понятием «нечеткое множество» тесно связано понятие «лингвистическая переменная», т.е. переменная, принимающая «лингвистические» значения (значение, выраженное на естественном языке). Эти значения называются термами. Человек в своих рассуждениях очень часто использует лингвистические переменные, например, «рост – малый» или «рост – высокий». В этих выражениях лингвистическая переменная «рост»
Н , C , В
1.0

v (м)
0 |
1.0 |
2.0 |
3.0 |
|
|
|
|
Рис.П3.3. Лингвистическая переменная рост.
134
принимает лингвистические значения «малый» и «высокий». Однако сказанным не исчерпывается понятие «лингвистической переменной». Дополнительно с каждым ее лингвистическим значением связывается нечеткое множество, степень принадлежности к которому задается на некотором базовом множестве V={v).
На рис.П3.3 приведено описание лингвистической переменной «рост» с тремя термами – «низкий», «средний» и «высокий» – базовым множеством будет множество численных значений роста.
Одним из языков описания алгоритмов, в том числе и алгоритмов управления, являются продукционные правила, которое имеет вид:
Продукционное правило при точной информации
Если «условие» То «заключение».
Если используемая в правиле информация, а также само правило неточны (ненадежны), то при описании могут быть использованы коэффициенты уверенности для характеризации условия (КУу), заключения (КУз) и правила в целом. Тогда правило принимает вид:
Продукционное правило при неточной информации
ПР. (КУпр):Если «условие» (КУу):То «заключение» (КУз)
При этом коэффициент уверенности для заключения определяется как произведение
КУз= КУпр* КУу.
Если условие и заключения правила сформулированы на языке событий, то в качестве коэффициентов уверенности могут быть использованы субъективно назначаемые вероятности.
В рамках нечеткого подхода в управлении продукционные правила также нашли применение в виде так называемых нечетких продукционных правил. В частности в модели Такаги-Сугено они используются для задания соответствия между нечеткими интервалами с одной стороны и частными наблюдателями и контроллерами с другой стороны.
Определение. Продукционное правило является нечетким, если в условии или заключении используются лингвистические переменные.
135
При этом оперирование правилами осуществляется в соответствии с процедурой нечеткого логического вывода, которая далее и будет
рассмотрена на примере задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
управления кондиционером. В |
|
|
|
|
T ,H , T ,C , T ,B |
|
|
|
|
||||||||||||||||
литературе описан |
целый |
ряд |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
процедур |
|
нечеткого |
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
логического |
выводы, |
которые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
характеризуются |
общностью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
структуры, но различаются по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОШ |
|
||||||||
ряду параметров. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Процедура |
нечеткого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
10 |
|
|
20 |
22 |
|
|
30 |
|
|
|
|
|
|
||||||||||
логического |
вывода |
всегда |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис.П3.4. Лингвистическая переменная |
|||||||||||||||||||||||||
содержит 5 этапов: |
|
|
|
||||||||||||||||||||||
Определение |
|
для |
всех |
температура воздуха в комнате. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
правил |
и |
для |
всех |
|
|
|
|
|
|
V ,H , V ,C , V ,B |
|
|
|
|
|||||||||||
условий |
|
степеней |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
принадлежности |
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
значений |
|
входных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
переменных |
|
нечетким |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
множествам, указанным в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V об/мин |
||||||||
условиях (фазификация). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определение |
|
степени |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
200 |
|
|
|
400 |
|
|
600 |
|
|
||||||||||||||
истинности для посылки |
|
|
|
|
|
|
|
|
|||||||||||||||||
в целом для |
каждого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис.П3.5. Лингвистическая переменная |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
правила (агрегирование). |
скорость вращения винтилятора. |
|
|
|
|
||||||||||||||||||||
Модификация нечетких множеств, указанных в заключении правил, в соответствии со
значениями степеней принадлежности, полученными на первом шаге.
Объединение (аккумулирование) модифицированных множеств.
Скаляризация результата объединения – переход от нечетких множеств
к скалярным значениям (дефазификация).
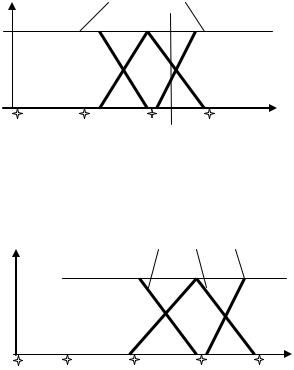
Выполним эти этапы по отношению к рассматриваемому примеру, используя процедуру Мамдани. Предварительно определим нечеткие множества для термов входных переменных правил. Для значений лингвистической переменной «температура воздуха в комнате» - высокая,
средняя, низкая |
- зададим соответствующие функции принадлежности |
T ,H , T ,C , T ,B на |
базовом множестве T значений температур (рис.П3.4). |
Аналогично для значений лингвистической переменной «скорость вращения вентилятора» – высокая, средняя, низкая – зададим функции принадлежностиV ,H , V ,C , V ,B на базовом множестве V значений скоростей (рис.П3.5).
Рассмотрим теперь, как определяется скорость вращение вентилятора в зависимости от температуры воздуха в комнате. Пусть эта температура равна 220 С . Сначала на первом этапе определим степени истинности условий правил вывода при подстановке в них текущего значения температуры. Для
136
этого надо определить степень принадлежности t |
= 220 С |
к каждому из |
||||||||||||||||||||
указанных |
в |
условиях |
нечетких |
множеств. Они |
соответственно |
равны: |
||||||||||||||||
T ,H 0, T ,C |
0.8, T ,B 0.2 . |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второй |
этап |
процедуры |
||
|
|
|
|
|
|
|
V ,H , V ,C , V ,B |
|
|
|
|
логического |
|
|
вывода |
|||||||
|
|
|
|
|
|
|
|
|
|
|
применительно |
|
к |
|||||||||
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматриваемому |
примеру не |
|||||
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет смысла, т.к. все три правила |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеют в |
посылке |
по |
одному |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0.2 |
|
|
|
|
|
|
|
|
|
|
|
V об/мин |
условию. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На третьем этапе полученные |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значения |
степеней |
истинности |
||
|
|
0 |
|
200 |
400 |
|
600 |
|
800 |
|||||||||||||
|
|
|
|
|
условий |
используются |
для |
|||||||||||||||
|
|
Рис. П3.6. Модификации нечетких |
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
модификации |
нечетких множеств, |
|||||||||||||||||
|
|
множеств, связанных с заключениями |
|
|||||||||||||||||||
|
|
правил. |
|
|
|
|
|
|
|
|
|
|
|
|
|
связанных с заключениями правил. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта модификация осуществляется |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
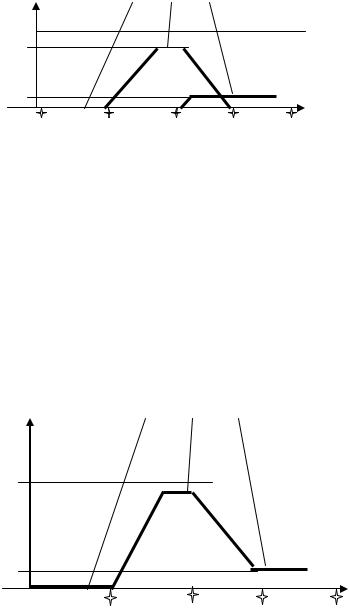
одним из двух методов – вычислением минимума или произведения. Первый ограничивает функцию принадлежности для нечеткого множества заключения значением истинности условия. Во втором методе значение истинности условия используется как коэффициент, на который умножается функция принадлежности заключения. Для каждого правила результат вычисляется отдельно. В процедуре Мамдани используется операция
минимума. Результат операции представлен на рис. П3.6. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Далее |
на |
4-м этапе |
||
|
|
V ,H , V ,C , V ,B |
|
|
|
|
|||||
|
|
|
|
|
необходимо |
|
|
обобщить |
|||
1.0 |
|
|
|
|
|
результаты |
действий |
всех |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
правил вывода, поскольку их |
||||||
|
|
|
|
|
|
||||||
0.8 |
|
|
|
|
|
заключения содержат одну и |
|||||
|
|
|
|
|
ту |
же |
лингвистическую |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
переменную |
|
|
«скорость |
||
0.2 |
|
|
|
|
|
вращения |
|
вентилятора». |
|||
|
|
|
V об/мин |
Суперпозиция |
|
результатов |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
правил |
может |
быть |
|||
|
|
|
|
|
|
осуществлена двумя методами |
|||||
0 |
200 |
400 |
600 |
800 |
– |
взятия |
максимума |
и |
|||
|
Рис.П3.7. Результат суперпозиции. |
|
суммирования. |
В |
процедуре |
||||||
|
|
|
|
|
|
Мамдани |
|
используется |
|||
|
|
|
|
|
|
операция |
|
|
максимума |
||
(рис.П3.7).
Конечный этап обработки – переход от нечетких значений к конкретным скалярным. Этот процесс часто называют дефазификацией. Для его реализации используются также два основных метода – вычисление «центра тяжести» фигуры и взятие максимума. В процедуре Мамдани используется метод центра тяжести. Центр тяжести фигуры находится в точке v = 550
137
об/мин. Это и будет значением скорости вентилятора, получаемое в результате логического вывода.
Литература
1.Андреев Ю.Н. Управление конечномерными линейными объектами. – М.: Наука, 1976. – 424 с.
2.Безмен Г.В., Колесов Н.В., Толмачева М.В. и др. Диагностирование систем реального времени // Приборы и системы. Управление, контроль, диагностика – 2008 – № 6. – С. 35 – 39.
3.Безмен Г.В., Колесов Н.В. Функциональное диагностирование линейных динамических систем с использованием нечеткого анализа // Информационно-управляющие системы – 2009 – № 6. – С.67 – 73.
4.Безмен Г.В., Колесов Н.В. Функциональное диагностирование динамических систем с использованием нечетких правил анализа и принятия решений об отказе // Известия РАН. Теория и системы управления – 2011 - №
3.– С. 3 – 12.
5.Бессекерский В.А., Попов Е.П. Теория систем автоматического управления. М.:Наука, 1975.
6.Бритов Г.С., Игнатьев М.Б., Мироновский Л.А., Смирнов Ю.М. Управление вычислительными процессами. – ЛГУ, 1973. 298 с.
7.Вентцель Е.С. Исследование операций. – М.: Советское радио,
1972.- 552 с.
8.Гильбо Е.П., Челпанов И.Б. Обработка сигналов на основе упорядоченного выбора. — М. Советское радио, 1975. 252 с.
9.Данилов В.В., Жирабок А.Н., Колесов Н.В., Шумский А.Е. Модель функционального диагностирования линейных цифровых систем//Электронное моделирование.- 1985.- № 1.- С.61-66.
10.Дмитриев С.П., Колесов Н.В., Осипов А.В. Информационная надежность, контроль и диагностика навигационных систем. – СПб.: Изд-во ЦНИИ «Электроприбор», 2003. 206 с.
11.Жирабок А.Н. Алгебраическая теория функционального диагностирования нелинейных и линейных динамических систем//Изв. АН РФ. Теория и системы управления.- 2001.- № 2.- С.29-38.
12.Жирабок А.Н., Шумский А.Е. Методы и алгоритмы функционального диагностирования сложных технических систем. Владивосток: Изд-во ДВГТУ, 2007. 134с.
13.Заде Л. Понятие лингвистической переменной и его применение для принятия приближенных решений.- М.: Мир, 1976. -165с.
14.Игнатьев М.Б., Мироновсий Л.А. и др. Контроль и диагностика робототехнических систем. Л.: Изд-во ЛИАП, 1985. 160 с.
15.Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. – М.: Советское радио, 1975.-
472с.
16.Колесов Н.В. Построение проверяющего теста для линейного конечного автомата // Автоматика и телемеханика, 1982, № 2, с. 61 – 66.
138
17.Колесов Н.В. Диагностирование линейных дискретных нестационарных систем // Автоматика и телемеханика, 1988, № 7, с. 157 –
163.
18.Колесов Н.В. Многоуровневое проектирование средств тестового
ифункционального диагностирования специализированных вычислительных комплексов. Л.: Изд-во ЦНИИ «Румб», 1992. 70 с.
19.Колесов Н.В. Нестационарная диагностическая модель системы обмена распределенного управляющего комплекса // Автоматика и телемеханика, 1990, № 4, с. 144 – 154.
20.Кофман А. Введение в теорию нечетких множеств. - М.: Радио и связь, 1982. - 432с.
21.Мироновский Л.А. Функциональное диагностирование динамических систем. М.-СПб.: Изд-во МГУ-ГРИФ, 1998. 256 с.
22.Основы технической диагностики. – Под ред. Пархоменко П.П., М.:Энергия, 1976. – 464 с.
23.Пархоменко П.П., Согомонян Е.С. Основы технической диагностики. – М.: Энергия, 1981.
24.Шаршунов С.Г. Построение тестов микропроцессоров. Ч.1. // Автоматика и телемеханика – 1985, № 11, с. 145 – 155.
25.Шумский А.Е. Поиск дефектов в нелинейных системах методом функционального диагностирования на основе алгебраических инвариантов // Электронное моделирование.- 1992.- № 1.- С.70-76.
26.Clark, R.N. A simplified instrument detection scheme // IEEE Trans. Aerospace Electron. Syst., 1978, Vol. 14, pp. 558-563 and 456-465.
27.Elghatwary M. G., Ding S. X., Gao Z. Robust fault detection for uncertain Takagi-Sugeno fuzzy systems with parametric uncertainty and process disturbances. // Proceedings of 6th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, Aug. 29 – Sep. 1, 2006, Beijing, China, pp. 271-276.
28.Frank, P.M. Advanced fault detection and isolation schemes using nonlinear and robust observers. // 10th IFAC, 1987, Congress, München, Vol. 3, pp. 63-68.
29.Frank P.M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy – A survey and some new results // Automatica. 1990. V. 26. P.459-474.
30.Isermann R. Model-based fault detection and diagnosis – status and applications // 16th IFAC Symposium on automatic control in aerospace, 2004, St.Petersburg, Russia, pp. 150-157.
31.Koscielny J.M. Application of fuzzy logic for fault isolation in a threetank system // Proc. 14th World Congress IFAC. Beijing. 1999. V. 7, pp. 73-78.
32.Koscielny J.M., Syfert M. fuzzy diagnostic reasoning that takes into account the uncertainty of the relation between faults and symptoms // Int. J. Appl.
Math. Comput. Sci., 2006, Vol. 16, № 1, 27–35.
139
33.Mendouca L. at al. Fault isolation using fuzzy model-based observers.
–6-th IFAC Symposium on Fault Detection. 2006. Beijing. P.R. China. P. 142150.
Patton R J, Frank P M, Clark R N. Issues in fault diagnosis for dynamic systems, Springer-Verlag, London, April 2000
140
