18. Точечные и интервальные оценки. Доверительная вероятность, доверительные интервалы.

Точечной оценкой некоторого параметра называют оценку, определяемую одним числом.

При выборках малого объема точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому при небольшом объеме выборки пользуются интервальными оценками.

Интервальной оценкой некоторого параметра 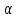называют числовой интервал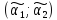, который с заданной вероятностью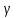покрывает значение параметра.

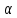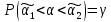
Где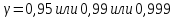

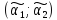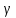Интервал называетсядоверительным интервалом, а вероятность называетсядоверительной вероятностью или надежностью оценки.

Оценки математического ожидания и среднего квадратического отклонения нормально распределенного признака.

1. Для оценки математического ожидания М (Х) = а нормально распределенного признака по выборочной средней и известному среднему квадратическому отклонению 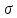служит следующий доверительный интервал:

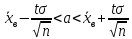
где 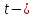значение аргумента интегральной функции Лапласа (в таблице № 2).

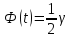
2. При исправленном среднем квадратическом отклонении S получим:

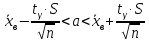
где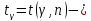значения в таблице № 3.

3. Доверительный интервал для оценки среднего квадратического отклонения 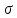при большом числе измерений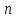имеет вид:

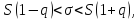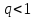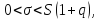при ,

при

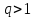
где 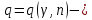значения в таблице № 4.

Пример 1.

Задана выборка значений признака X, имеющего нормальное распределение:

	‒2	1	2	3	4	5
	2	1	2	2	2	1

Найти: а) выборочную среднюю 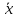и исправленное среднее квадратическое отклонениеs; б) указать доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание а признака X; в) указать доверительный интервал, покрывающий с надежностью 0,95 среднее квадратическое отклонение 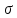признакаX.

Решение:

а) Вычисляем объем выборки: .

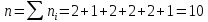Тогда

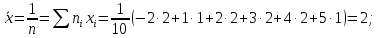
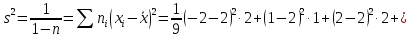
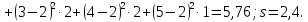
б) Искомый доверительный интервал для математического ожидания а имеет вид:

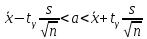
где 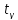находим по таблице приложения 2. При= 0,95n = 10 получаем 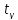= 2,26. Тогда

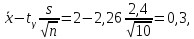
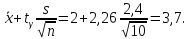
Таким образом,

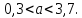
в) Доверительный интервал для генерального среднего квадратического отклонения а имеет вид:

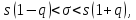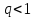
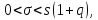если

если

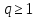
Соответствующие значения q указаны в таблице приложения 3. По заданным 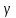= 0,95 иn = 10 находим q = 0,65. Теперь искомый доверительный интервал запишется следующим образом:

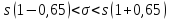
или

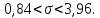
Методические указания по выполнению контрольных работ и выбору варианта

1. При выполнении контрольной работы студент должен руководствоваться следующими указаниями:

2. Работа должна выполняться в тетради (в клеточку) с полями, на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, специальность, номер группы, номер варианта.

3. Задачи располагаются в порядке номеров. Перед решением надо полностью переписать условие задачи.

4. Решение задач следует излагать подробно с указанием необходимых формул.

5. Задача геометрического содержания должна сопровождаться чертежом, выполненным аккуратно с указанием осей координат и единиц масштаба.

6. Контрольная работа должна выполняться самостоятельно. Если преподаватель установит несамостоятельность выполнения работы, то она не будет зачтена.

7. Студент должен исправить все недочеты и ошибки, указанные преподавателем в прорецензированной работе, после чего пройти собеседование по контрольной работе.

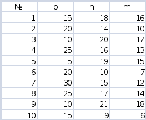
8. Вариант определяется по двум последним цифрам шифра по схеме:

1. По предпоследней цифре учебного шифра зачетной книжки выбирается номер строки;

2. По последней цифре учебного шифра зачетной книжки выбирается номер столбца;

3. На пересечении строки и столбца находится номер варианта.

9. Зачтенная контрольная работа является допуском студента к экзамену или зачету.

Для решения задач необходимо изучить следующие вопросы:

1. .Основные понятия и теоремы теории вероятностей.

2. Повторные независимые испытания. Формулы Бернулли, Муавра – Лапласа, Пуассона.

3. Случайные величины и их числовые характеристики.

4. Основные законы распределения.

5. Основные понятия математической статистики.

6. Понятие оценки параметров. Методы нахождения оценок.

Задание №1.

№№ 1-10. Три орудия производят по одному выстрелу в цель независимо друг от друга. Вероятность попадания в цель для каждого из них равны соответственно m, n, k. Найти вероятность того что:

а) в цель попадёт только одно орудие; б) в цель попадут только два орудия;

в) в цель попадёт хотя бы одно орудие.

1. n=0,7; m=0,9; k=0,8. 6. n=0,65; m=0,7; k=0,9.

2. n=0,6; m=0,9; k=0,9. 7. n=0,8; m=0,6; k=0,85.

3. n=0,8; m=0,8; k=0,7. 8. n=0,7; m=0,75; k=0,9.

4. n=0,75; m=0,6; k=0,8. 9. n=0,85; m=0,6; k=0,7.

5. n=0,9; m=0,7; k=0,75. 10. n=0,95; m=0,8; k=0,65.

№№ 11-20. Три студента участвуют независимо друг от друга в олимпиаде по математике. Вероятности победы для каждого из них равны соответственно m₁, m₂, m₃. Какова вероятность того, что:

а) победит только один студент; б) победу разделят два студента;

в) победит хотя бы один студент.

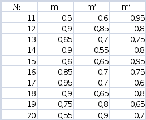
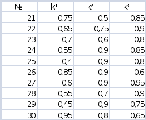
№№ 21-30. Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике, соответственно равны k₁, k₂, k₃. Найти вероятность того, что разыскиваемая формула содержится:

а) только в одном справочнике;

б) только в двух справочниках;

в) хотя бы в одном справочнике.

Задание №2.

№№ 1-10. Из урны, содержащей n белых и m красных шаров наугад вынимают два шара. Какова вероятность того, что:

а) оба шара красные; б) один шар белый, другой – красный;

в) хотя бы один шар белый.

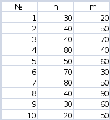
№№ 11-20. В академической группе обучается n студентов, среди которых m девушек. На уборку территории выбирают произвольно трёх студентов. Какова вероятность того, что:

а) все три студента - юноши; б) два студента – юноши, один студент – девушка;

в) хотя бы один студент – юноша.

№№ 21-30. В коробке находиться n одинаковых изделий, причём m из них окрашены. Найти вероятность того, что среди двух извлечённых наугад изделий окажутся:

а) одно окрашенное изделие; б) два окрашенных изделия;

в) хотя бы одно окрашенное изделие.

Задание №3.

В вычислительной лаборатории имеются m автоматов и n полуавтоматов. Вероятность того, что за время выполнения некоторого расчёта автомат не выйдет из строя, равна p′; для полуавтомата эта же вероятность равна p″. Студент производит расчёт на удачу выбранной машине. Определить вероятность того, что до окончания расчёта выбранная машина не выйдет из строя.

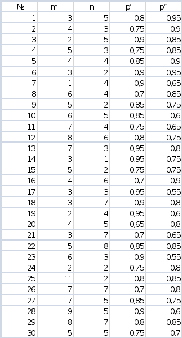
Задание №4.

№№ 1 – 8. У рыбака есть три излюбленных места рыбалки. Эти места он посещает с одинаковой вероятностью. Вероятность того, что рыба клюнет в первом месте, близка к - р₁, во втором месте – р₂, в третьем месте – р₃. Известно, что рыбак забросил удочку один раз. Какова вероятность, что он поймал рыбу в первом из излюбленных мест?

1. р₁ = 0,13; р₂ = 0,14; р₃ = 0,12

2. р₁ = 0,23; р₂ = 0,12; р₃ = 0,13

3. р₁ = 0,12; р₂ = 0,14; р₃ = 0,34

4. р₁ = 0,15; р₂ = 0,13; р₃ = 0,23

5. р₁ = 0,14; р₂ = 0,34; р₃ = 0,25

6. р₁ = 0,35; р₂ = 0,13; р₃ = 0,12

7. р₁ = 0,45; р₂ = 0,23; р₃ = 0,15

8. р₁ = 0,13; р₂ = 0,23; р₃ = 0,25

№№ 9 – 16. Студент может купить билет в одной из трёх касс автовокзала. Вероятность того, что он направится к первой кассе, примерно равна – 0,12, ко второй – 0,13, к третей – 0,16. Вероятности того, что билетов уже нет в кассах, примерно такие: в первой кассе – р₁, во второй – р₂, в третей – р₃. Какова вероятность того, что он купил билет? Определить вероятность того, что он купил билет во второй кассе?

9. р₁ = 0,15; р₂= 0,16; р₃= 0,18.

10. р₁ = 0,25; р₂= 0,13; р₃= 0,14.

11. р₁ = 0,35; р₂= 0,12; р₃= 0,38.

12. р₁ = 0,45; р₂= 0,23; р₃= 0,17.

13. р₁ = 0,16; р₂= 0,25; р₃= 0,27.

14. р₁ = 0,14; р₂= 0,18; р₃= 0,35.

15. р₁ = 0,13; р₂= 0,16; р₃= 0,15.

16. р₁ = 0,12; р₂= 0,13; р₃= 0,14.

№№ 17 – 24 Семена для посева в хозяйство поступают из трёх семеноводческих хозяйств. Причём первое и второе хозяйство присылают по 40 % всех семян. Всхожесть семян из первого хозяйства – р₁, второго – р₂, третьего – р₃.

1. Определить вероятность того, что наудачу взятое семя не взойдёт.

2. На удачу взятое семя не взошло. Какова вероятность, что оно получено от второго хозяйства?

9. р₁ = 90%; р₂ = 85%; р₃ = 95%

10. р₁ = 80%; р₂ = 93%; р₃ = 82%

19. р₁ = 78%; р₂ = 94%; р₃ = 85%

20. р₁ = 87%; р₂ = 89%; р₃ = 79%

21. р₁ = 91%; р₂ = 93%; р₃ = 86%

22. р₁ = 92%; р₂ = 88%; р₃ = 77%

23. р₁ = 97%; р₂ = 83%; р₃ = 88%

24. р₁ = 90%; р₂ = 81%; р₃ = 84%

№№ 25 – 30. Покупатель с равной вероятностью посещает каждый из трёх магазинов. Вероятность того, что покупатель приобретёт товар в первом магазине равна – р₁, втором – р₂, в третьем – р₃. Определить вероятность того, что покупатель приобретёт товар в каком – либо магазине. Покупатель приобрёл товар. Найти вероятность того, что он купил его во втором магазине?

19. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

20. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

21. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

22. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

23. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

24. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

Задание №5.

№№ 1-10. Всхожесть семян данного растения составляет p%. Какова вероятность того, что из n посеянных семян взойдут:

а) m семян;

б) не менее m семян.

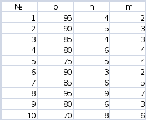
№№ 11-20. В водоёме лососи составляют q%. Найти вероятность того, что из n пойманных в этом водоёме рыб окажется:

а) m лососей;

б) не более m лососей.

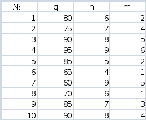
№№ 21-30. В партии деталей число бракованных составляет p%. Какова вероятность того, что среди взятых наудачу n деталей не бракованные окажутся:

а) m деталей;

б) менее m деталей.

Задание №6.

№№ 1-6. Вероятность поражения цели при каждом выстреле равна p. Найти наивероятнейшее число попаданий в серии из n выстрелов и вычислить вероятность соответствующего события.

1. p=0,2 n=5

2. p=0,3 n=6

3. p=0,35 n=4

4. p=0,25 n=7

5. p=0,4 n=3

6. p=0.15 n=8

8. №№ 7-12. Всхожесть семян растения данного сорта составляет m%. Посеяли n семян. Найти наивероятнейшее число всходов и вычислить вероятность соответствующего события.

10. m=90 n=8

11. m=80 n=5

12. m=95 n=6

13. m=85 n=7

14. m=70 n=4

15. m=75 n=9

17. №№ 13-24. На склад поступило n ящиков, содержащих стеклянные изделия. Вероятность того, что в любом ящике окажется битое изделие, равна p. Найти наивероятнейшее число ящиков, содержащих неповреждённые изделия и вычислить соответствующего события.

19. 13,19. p=0,75 n=8

20. 14,20. p=0,4 n=6

21. 15,21. p=0,55 n=7

22. 16,22. p=0,6 n=9

23. 17,23. p=0,7 n=10

24. 18,24. p=0,65 n=11

25. №№ 25-30. Вероятность того, что любой из лотерейных билетов окажется выигрышным, равна p. Приобретено n билетов. Найти наивероятнейшее число выигрышных среди них, и вычислить вероятность соответствующего события.

27. 25. p=0,3 n=6

28. 26. p=0,45 n=7

29. 27. p=0,55 n=8

30. 28. p=0,4 n=10

31. 29. p=0,5 n=9

32. 30. p=0,35 n=11

34. Задание №7.

36. №№ 1-10. Баскетболист забрасывает штрафной примерно с вероятностью p. Какова вероятность того, что среди n бросков будут удачными:

37. а) все броски;

38. б) не менее k₁ и не более k₂ бросков.

1. n=20 p=0,8 k₁=15 k₂=18

2. n=18 p=0,7 k₁=10 k₂=15

3. n=12 p=0,85 k₁=8 k₂=12

4. n=20 p=0,6 k₁=16 k₂=19

5. n=18 p=0,9 k₁=14 k₂=18

6. n=19 p=0,8 k₁=13 k₂=16

7. n=16 p=0,75 k₁=11 k₂=15

8. n=20 p=0.3 k₁=4 k₂=10

9. n=15 p=0,5 k₁=5 k₂=9

10. n=19 p=0,45 k₁=7 k₂=11

41. №№ 11-20. Вероятность рождения девочки равна p. Чему равна вероятность того, что среди n новорождённых:

42. а) все девочки;

43. б) не менее k₁ и не более k₂ девочек.

45. 11. n=30 p=0,485 k₁=13 k₂=18

46. 12. n=32 p=0,48 k₁=10 k₂=20

47. 13. n=29 p=0,49 k₁=10 k₂=18

48. 14. n=26 p=0,495 k₁=8 k₂=14

49. 15. n=31 p=0,475 k₁=12 k₂=16

50. 16. n=33 p=0,47 k₁=13 k₂=17

51. 17. n=34 p=0,46 k₁=12 k₂=19

52. 18. n=35 p=0,465 k₁=14 k₂=20

53. 19. n=36 p=0,45 k₁=12 k₂=17

54. 20. n=33 p=0,455 k₁=13 k₂=16

55. №№ 21-30. Вероятность того, что саженец ели прижился, и будет расти примерно равна p. Посажено n саженцев ели. Какова вероятность того, что нормально вырастут:

56. а) все посаженные ели;

57. б) не менее k₁ и не более k₂ елей.

59. 21. n=400 p=0,8 k₁=300 k₂=340

60. 22. n=420 p=0,75 k₁=310 k₂=320

61. 23. n=350 p=0,9 k₁=300 k₂=330

62. 24. n=300 p=0,85 k₁=240 k₂=270

63. 25. n=320 p=0,95 k₁=290 k₂=318

64. 26. n=450 p=0,7 k₁=290 k₂=330

65. 27. n=500 p=0,65 k₁=315 k₂=335

66. 28. n=440 p=0,55 k₁=222 k₂=262

67. 29. n=480 p=0,5 k₁=220 k₂=260

68. 30. n=380 p=0,6 k₁=200 k₂=256

69. Задание №8.

70. Две независимые дискретные случайные величины X и Y заданы своими законами распределения. Найти математическое ожидание и дисперсию для случайной величины W=2X – 3Y

1. X -3 -7 1 2 Y 2 4

71. Y 0,1 0,2 0,2 0,5 P 0,7 0,3

2. X -3 2 6 4 Y 3 6

73. Y 0,3 0,3 0,2 0,2 P 0,8 0,2

3. X -5 1 2 4 Y 2 4

75. Y 0,2 0,3 0,1 0,4 P 0,6 0,4

4. X -4 0 2 5 Y 3 5

77. Y 0,1 0,5 0,2 0,2 P 0,2 0,8

5. X -2 -1 3 7 Y 1 6

79. Y 0,1 0,3 0,3 0,3 P 0,3 0,7

6. X -3 -1 0 2 Y 0 4

81. Y 0,2 0,3 0,4 0,1 P 0,9 0,1

7. X -5 -2 3 2 Y 1 7

83. Y 0,1 0,6 0,1 0,2 P 0,4 0,6

8. X -4 -1 3 8 Y 2 3

85. Y 0,1 0,3 0,5 0,1 P 0,7 0,3

9. X -7 0 1 2 Y -4 4

87. Y 0,5 0,1 0,1 0,3 P 0,3 0,7

10. X -2 -1 0 1 Y -3 4

90. Y 0,4 0,4 0,1 0,1 P 0,2 0,8

11. X -8 -6 -1 5 Y -2 1

92. Y 0,6 0,1 0,2 0,1 P 0,8 0,2

12. X -7 -4 0 3 Y -4 3

94. Y 0,3 0,3 0,1 0,3 P 0,1 0,9

13. X -2 0 1 4 Y -6 3

96. Y 0,3 0,2 0,3 0,2 P 0,4 0,6

14. X -6 -3 -2 3 Y -8 2

98. Y 0,1 0,2 0,4 0,3 P 0,7 0,3

15. X -5 -4 -2 2 Y -3 3

100. Y 0,1 0,3 0,4 0,2 P 0,6 0,4

16. X -2 -1 3 4 Y -4 0

102. Y 0,2 0,2 0,2 0,4 P 0,9 0,1

17. X -3 3 4 6 Y 0 3

104. Y 0,1 0,2 0,3 0,4 P 0,2 0,8

18. X -6 -2 1 2 Y -1 3

106. Y 0,3 0,3 0,2 0,2 P 0,7 0,3

19. X -2 -1 1 2 Y 1 3

108. Y 0,6 0,1 0,1 0,2 P 0,4 0,6

20. X -4 -3 0 4 Y -2 3

110. Y 0,3 0,5 0,1 0,1 P 0,5 0,5

21. X -6 -5 3 4 Y 0 3

112. Y 0,2 0,2 0,2 0,4 P 0,4 0,6

22. X -7 -2 2 7 Y -3 0

114. Y 0,2 0,4 0,1 0,3 P 0,5 0,5

23. X -3 -2 3 4 Y -4 1

116. Y 0,3 0,4 0,1 0,2 P 0,6 0,4

24. X -7 0 1 3 Y -1 1

118. Y 0,3 0,2 0,3 0,2 P 0,4 0,6

25. X -4 -3 0 4 Y 0 3

120. Y 0,5 0,3 0,1 0,1 P 0,9 0,3

26. X -5 -2 2 6 Y -3 1

122. Y 0,3 0,2 0,4 0,1 P 0,5 0,5

27. X -9 0 1 2 Y -3 0

124. Y 0,7 0,1 0,1 0,1 P 0,7 0,3

28. X -6 -5 -4 2 Y -1 4

126. Y 0,2 0,6 0,1 0,1 P 0,2 0,8

29. X -1 0 3 4 Y -1 7

128. Y 0,3 0,1 0,3 0,3 P 0,9 0,1

30. X -4 -3 -2 8 Y -4 2

130. Y 0,5 0,1 0,2 0,2 P 0,3 0,7

133. Задание №9

134. В задачах 1 – 30 задана выборка значений нормально распределённого признака X (даны значения признака x_i и соответствующие им частоты n_i). Найти: а) выборочную среднюю x и исправленное среднее квадратическое отклонение s; б) доверительный интервал, покрывающий неизвестное математическое ожидание a признака X; в) доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение g признака X (надёжность оценки во всех вариантах считать равной y=0,95).

1. x_i -3 1 2 4 5 7

135. n_i 1 2 2 3 2 4

2. x_i -5 -2 3 4 6 7

136. n_i 2 3 1 3 4 5

3. x_i -3 -2 1 2 4 6

137. n_i 3 2 2 4 5 1

4. x_i -5 -4 2 4 7 8

138. n_i 1 2 4 5 4 3

5. x_i -6 -4 -3 2 3 5

139. n_i 2 4 6 1 3 5

6. x_i -2 -1 1 3 5 6

140. n_i 1 2 4 6 3 1

7. x_i -7 -6 -4 2 3 5

141. n_i 1 3 5 3 4 2

8. x_i -3 -2 1 4 5 7

142. n_i 2 4 6 1 3 3

9. x_i -5 -2 -1 2 4 6

143. n_i 1 4 6 5 1 3

10. x_i -6 -2 -1 3 5 7

144. n_i 1 2 4 4 5 1

11. x_i -3 1 4 5 7 8

145. n_i 4 2 3 5 1 1

12. x_i -3 -2 1 3 4 7

146. n_i 1 4 4 3 5 1

13. x_i -3 -1 3 4 5 6

147. n_i 2 4 5 4 3 2

14. x_i -5 -4 1 3 6 8

148. n_i 2 3 3 4 3 1

15. x_i 2 4 5 7 8 9

149. n_i 1 4 3 3 4 1

16. x_i -2 -1 1 3 5 6

151. n_i 2 2 3 1 4 5

17. x_i -1 2 3 5 7 9

152. n_i 2 3 5 5 1 1

18. x_i -5 -4 6 7 8 9

153. n_i 3 3 1 4 2 2

19. x_i -4 -2 -1 3 5 6

154. n_i 1 5 5 4 3 1

20. x_i -2 -1 2 4 5 7

155. n_i 1 5 5 1 3 3

21. x_i -4 -2 -1 2 3 7

156. n_i 1 4 4 3 1 2

22. x_i -5 -3 -1 2 4 7

157. n_i 2 1 1 4 3 2

23. x_i -3 -2 1 3 5 8

158. n_i 1 2 4 3 2 1

24. x_i -4 -3 2 3 4 6

159. n_i 2 4 3 5 2 2

25. x_i -3 -1 2 4 5 6

160. n_i 1 3 4 5 2 1

26. x_i -6 -3 -1 2 3 5

161. n_i 2 4 5 4 3 2

27. x_i -5 -4 2 4 7 8

162. n_i 1 3 3 5 4 2

28. x_i -3 -2 1 4 5 7

163. n_i 1 4 6 5 1 3

29. x_i -1 2 3 5 7 9

164. n_i 1 4 3 3 4 1

30. x_i -6 -4 -3 2 3 5