Электричество (Лабораторный практикум часть 3)
.pdf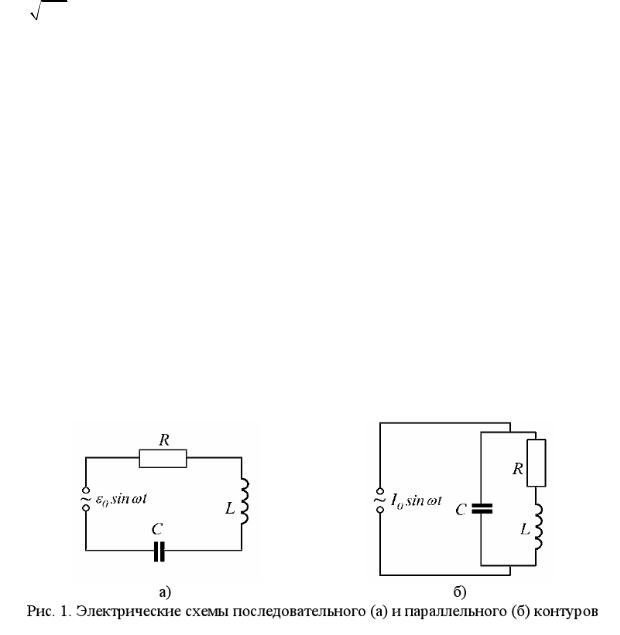
где q – заряд конденсатора,2 R/L ( - коэффициент затухания контура);
0 1/
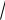LC - круговая частота свободных электрических колебаний контура.
С течением времени свободный колебательный процесс в контуре будет затухать. Для получения незатухающих колебаний необходимо непрерывно пополнять запас энергии контура, чтобы скомпенсировать потери. С этой целью контур подключается к генератору переменного тока. Незатухающие колебания, возникающие в контуре, называются вынужденными, поскольку их частота определяется частотой генератора. В этом случае дифференциальное уравнение колебательного процесса примет вид:
d2q |
2 |
dq |
2q F cos( t) |
(2) |
||
dt2 |
dt |
|||||
|
0 |
0 |
|
|||
В настоящей задаче исследуются вынужденные колебания в колебательном контуре, элементами которого являются конденсатор C , индуктивность L и активное сопротивление R , соединенные последовательно (рис. 1,а) или параллельно (рис. 1,б) с источником питания. При этом в качестве источника питания используется либо генератор переменной ЭДС (рис. 1,а), либо генератор переменного тока (рис. 1,б).
Последовательное соединение элементов контура
Рассмотрим электрическую цепь, включающую в себя внешний источник, ЭДС которого меняется по гармоническому закону конденсатор C, индуктивность L и активное сопротивление R (см. рис. 1а). Записывая закон Кирхгофа для этой цепи, получим уравнение вынужденных колебаний в контуре:
L |
dI |
RI |
q |
|
|
sin( t) |
(3) |
dt |
|
0 |
|||||
|
|
C |
|
|
|||
21
где I - ток, протекающий в контуре; q - заряд на пластине конденсатора; ε0 - амплитуда напряжения источника ЭДС; ω - частота источника ЭДС. Так как сила тока I=dq/dt, то уравнение (3) можно записать в следующем виде
L |
d2q |
R |
dq |
|
q |
|
|
sin( t) |
(4) |
||
dt |
2 |
dt |
C |
0 |
|||||||
|
|
|
|
|
|
||||||
Разделим обе части уравнения (4) на L и введя обозначения
R/2L ,
(5)
1/LC 02
где ω0 - собственная частота колебательного контура в отсутствие затухания, δ - коэффициент затухания колебаний.
С учетом обозначений (5) уравнение (4) может быть преобразовано к следующему виду:
d2q |
|
dq |
2 |
q |
|
/Lsin( t) |
|
|
2 |
|
|
|
(6) |
||
dt2 |
dt |
|
|||||
|
0 |
|
0 |
|
|
Для установившихся колебаний решение этого уравнения будет выглядеть так:
|
q q0 sin( t ) |
|
|
|
(7) |
|||
где |
0 |
|
|
|
|
|
||
q0 |
|
|
|
|
|
, |
(8) |
|
|
|
|
|
|
|
|||
L ( 2 |
2)2 |
4 2 |
|
|||||
|
2 |
|
||||||
0 |
|
|
|
|
|
|
||
tg |
2 |
|
(9) |
2 |
2 |
||
|
|
|
|
|
0 |
|
|
Соотношения для тока в цепи
Используя выражение (7) для q, можно установить закон изменения силы тока в цепи:
I |
dq |
q cos( t ) q sin( t ), |
|
||||||
dt |
|
||||||||
|
0 |
|
0 |
(10) |
|||||
|
|
|
2 2 |
|
L |
1 |
|
|
|
|
|
|
|
C |
|
||||
tg |
0 |
|
|
, |
|
||||
|
|
|
|
||||||
|
|
|
2 |
|
R |
|
|||
22
где = - /2 - разность фаз между ЭДС и током в цепи, I0=q0 - амплитуда колебаний силы тока в цепи.
С учетом (8) можно записать выражение для зависимости амплитуды тока в цепи от частоты ЭДС:
I0 q0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
L ( 2 |
- 2)2 |
|
|
|
|
1 |
|
|
|||||||
|
4 2 2 |
R |
2 |
( L- |
) |
2 |
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
C |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из формулы (11) видно, что амплитудное значение силы тока зависит от частоты ω. Рассмотрим полученные результаты подробнее. При ω = 0
амплитуда тока |
I0=0. С |
ростом частоты I0 возрастает |
и при |
= 0 = (1/LC)1/2 |
амплитуда |
тока достигает максимального |
значения |
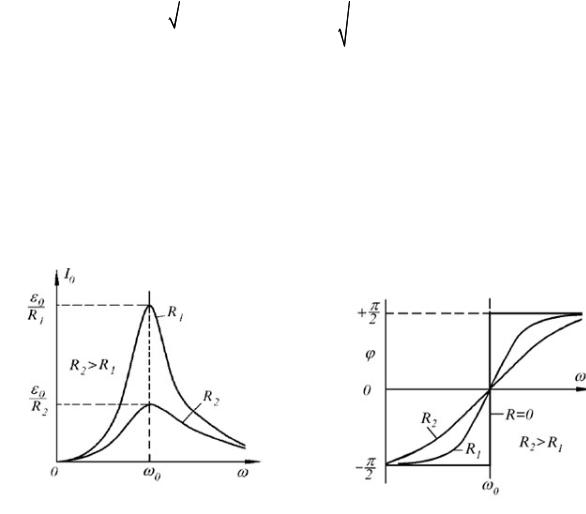
I0 = 0/2 L = 0/R , разность фаз φ при этом равна нулю. При дальнейшем увеличении частоты I0 уменьшается, и при ω → ∞ амплитуда тока I0 → 0. В итоге зависимость I0 (ω) имеет вид, представленный на рис. 2 (для двух значений активного сопротивления). Эта зависимость получила название амплитудно-частотной характеристики контура.
Рис. 2. Зависимость I0 от частоты |
Рис. 3. Зависимость от часто- |
для двух значений R |
ты для двух значений R |
Из рис. 2 видно, что чем меньше R (меньше коэффициент затухания δ), тем больше I0 и тем «острее» максимум кривой.
На рис. 3 приведены зависимости разности фаз φ между ЭДС и током в цепи от частоты ω. Видно, что при частотах, близких к нулю, разность близка к - /2 (говорят, что напряжение отстает по фазе от тока на /2). При больших частотах разность фаз стремится к + /2 (напряжение опережает ток по фазе на /2). При частоте ω = ω0 разность фаз равна нулю. Из рис.3 видно, что чем меньше R, тем быстрее изменение φ вблизи частоты ω = ω0. В предельном случае при R = 0 фаза изменяется скачком при ω = 0.
23
Найдем теперь зависимость напряжения на конденсаторе от частоты ω. Так как q= Idt , то, проинтегрировав выражение (10), получим:
|
q |
1 |
I0 sin( t )dt |
I0 |
||
UC |
|
|
|
|
cos( t ) UC0 sin( t C ) (12) |
|
C |
C |
C |
||||
где
UC0 |
|
0 |
|
(13) |
||
|
|
|
|
|
||
C R2 ( L- |
1 |
)2 |
||||
|
|
|
|
|||
|
|
|
C |
|
|
|
– амплитуда колебаний напряжения на конденсаторе, С = + /2 - разность фаз между ЭДС и напряжением на конденсаторе. При ω = ω0 получим:
U |
C0 |
|
0 |
|
0 |
|
|
|
0 |
|
L |
|
Q |
(14) |
||
|
|
|
|
|
|
|
||||||||||
|
|
0CR |
|
CR |
|
1 |
|
|
|
R |
|
C |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
LC
где Q 1 L - добротность контура. Значение добротности характери-
R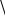 
C
зует величину потерь энергии в контуре - чем меньше потери, тем больше добротность. Из формулы (14) видно, что при ω = ω0 напряжение на конденсаторе в Q раз больше ЭДС источника. Это явление носит название резонанса напряжений. Можно показать, что амплитуда колебаний напряже-
ния на индуктивности UL0 LdI при ω = ω0 также будет равна ε0Q, но при dt
этом напряжение на индуктивности будет меняться в противофазе с напряжением на конденсаторе.
Из формулы (13) можно найти частоту ωC , при которой напряжение на конденсаторе будет максимальным. Для этого надо решить уравнение
dUC0 0. После несложных, но громоздких преобразований можно полу- d
чить:
2 |
1 |
|
R 2 |
|
|
|
|
|
|
1 |
|
|
|
||||
C 0 |
|
|
|
|
|
|
0 |
|
1 |
|
|
|
0 |
||||
|
|
|
2Q |
2 |
|||||||||||||
|
2 |
|
L |
|
|
|
|
|
|
|
(15) |
||||||
UC0( C ) |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
CR |
1 |
|
R2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
LC |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
4L |
|
|
|
|
|
|
|
|
||
При Q>>1 можно записать ωС ≈ ω0, а UC0( C ) 0Q.
24
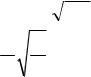
По определению, добротность Q= /q, где θ - логарифмический декремент затухания свободных колебаний в контуре. В свою очередь, θ = δT,
где T 2 / |
2 |
2 |
(затухание мало, |
|
0 |
|
|
поэтому 20 2 ), и после несложных преобразований можно получить фор-
мулу Q |
1 |
|
L |
. Также для добротно- |
R |
|
|||
|
|
C |
||
сти часто |
|
приводят формулу Q |
||
= 2 Wзапас/Wрасс, где Wзапас – энергия,
запасенная в контуре, и Wрасс – потери энергии в контуре за период колебаний.
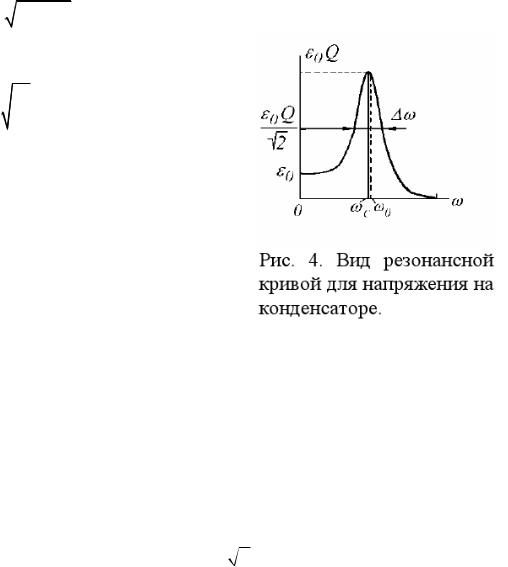
Таким образом, измеряя напряжение на конденсаторе на резонансной частоте, можно определить добротность контура Q. На рис. 4 приведена зависимость амплитуды напряжения
на конденсаторе от частоты ЭДС внешнего источника.
При ω = 0 UC0 = ε0, по мере увеличения частоты UC0 растет и при = 0 достигает своего максимального значения, после чего начинается монотонное убывание напряжения до нуля. Обратим внимание на тот факт, что частота ωC, при которой амплитуда колебаний напряжения на конденсаторе максимальна, несколько меньше частоты ω0, для которой максимальна амплитуда силы тока.
Обычно вводится понятие ширины резонансной кривой ∆ω - это диапазон частот, для которых амплитуда напряжения отличается от амплитуды напряжения в резонансе не более, чем в 
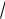2 раз.
Можно показать, что для ∆ω<<ω0 справедливо соотношение Q 0 / . Таким образом, определяя ширину резонансной кривой, можно также найти добротность контура Q.
График зависимости разности фаз между напряжением источника ЭДС и напряжением на конденсаторе будет иметь такой же вид, как на рис. 3, только «приподнятый» на /2, т. к. С = + /2. Иными словами, в точке резонанса, когда ток и напряжение источника совпадают по фазе, напряжение на конденсаторе будет отставать по фазе от напряжения источника на
/2.
Напряжение на конденсаторе всегда (а не только при резонансе) отстает по фазе от тока, протекающего через конденсатор, на /2, в свою очередь, напряжение на индуктивности всегда опережает по фазе ток на /2.
25
Параллельное соединение элементов контура
Для рассмотрения параллельного соединения элементов контура учтем, что если участок цепи содержит только активное сопротивление R, либо только конденсатор емкостью C, либо только катушку индуктивности L, то соответствующие выражения для импеданса имеют вид:
ZR R, |
ZC 1/ j C, |
ZL j L. |
Зная эти соотношения и применяя законы Кирхгофа к цепям переменного тока, можно сформулировать следующее правило для расчета комплексного сопротивления цепи: поставить в соответствие каждому элементу цепи его комплексное сопротивление, а затем использовать правила вычисления суммарного сопротивления цепи для постоянного тока. Тогда при последовательном соединении сопротивления складываются, при параллельном - складываются обратные величины (проводимости).
На основании рис. 1,б можно записать соотношение
1 |
|
1 |
|
j C , |
|
(16) |
|||
|
|
Z |
|
|
|
||||
|
|
|
R j L |
|
|
||||
или |
|
|
|
|
|
|
|
||
Z |
R j L |
|
R j L |
. |
(17) |
||||
|
|
|
|
||||||
1 j C(R j L) |
|
1 2CL j CR |
|
|
|||||
Умножая числитель и знаменатель (17) на (1 2LC) j RC, получа-
ем:
|
R j |
|
2 |
2 |
|
|
Z |
L(1 |
LC) R C |
|
(18) |
||
(1 2LC)2 ( RC)2 |
|
|||||
|
|
|
||||
При равенстве мнимой части импеданса нулю, т. е. при выполнении соотношения:
L(1 2LC) CR2 0,
сопротивление цепи эквивалентно омическому.
Решая уравнение (19) относительно ω = рез, получаем:
2 |
|
L CR2 |
2 |
R2 |
C |
2 |
2 |
(1 |
1 |
), |
L2C |
|
Q2 |
||||||||
рез |
|
0 |
|
L 0 |
0 |
|
|
|||
(19)
(20)
где 0 1/
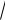LC - собственная частота незатухающих колебаний в контуре;
Q 1 L - добротность контура.
R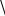 
C
Можно показать, что в этом случае модуль импеданса принимает максимальное значение, равное:
26
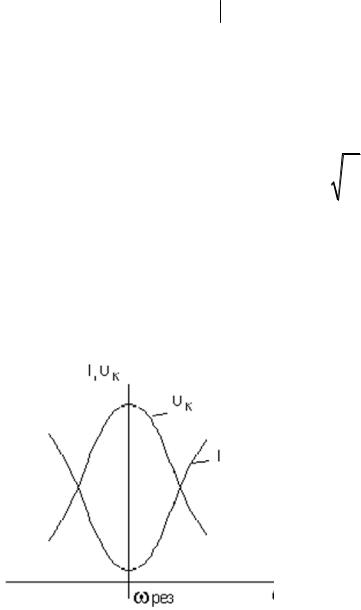
Z |
|
|
L |
RQ2 |
(21) |
|
|||||
|
|
||||
|
|
|
CR |
|
|
|
|
|
|
||
Для частоты рез падение напряжение на контуре UК будет максимальным: UK LI / CR, а общий ток цепи I минимален.
Можно рассчитать комплексную амплитуду силы тока, протекающего через конденсатор в этом случае (при Q>>1):
I |
|
|
|
|
U |
K |
|
|
|
LI рез |
С |
1 |
|
L |
I QI |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
|||
|
|
ZC |
|
|
CR |
|
R |
|
C |
||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, ток, протекающий через конденсатор, по модулю в Q раз больше тока, даваемого генератором.
Если активное сопротивление контура R равно нулю (идеальный контур), то результирующее значение тока во внешней цепи контура будет равно нулю, т. е. сопротивление идеального параллельного колебательного контура при резонансе бесконечно
|
велико (Zрез= ). |
|
|
Для проверки данного соотно- |
|
|
шения достаточно подставить вы- |
|
|
ражение (20) в формулу (18) с уче- |
|
|
том равенства активного сопротив- |
|
|
ления нулю (R=0). В реальном кон- |
|
|
туре часть энергии расходуется в |
|
|
активном сопротивлении, т. е. в |
|
|
контуре могут существовать только |
|
|
затухающие колебания и результи- |
|
|
рующий ток во внешней цепи не |
|
Рис.5. Резонансные кривые тока |
равен нулю, но достигает своего |
|
минимального значения. |
||
во внешней цепи I и напряжения Uк |
||
На рис.5 приведены резонанс- |
||
параллельного колебательного кон- |
||
ные кривые тока во внешней цепи I |
||
тура. |
и напряжения параллельного коле- |
|
|
||
|
бательного контура UК. |
|
|
Таким образом контур, состоя- |
щий из параллельно соединенных емкости и индуктивности с очень малым омическим сопротивлением, представляет очень большое сопротивление для узкой полосы частот вблизи резонансной частоты.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
27
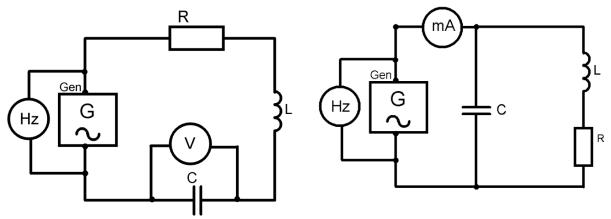
Исследование явления резонанса проводится на экспериментальной установке ФЭЛ-1 по схемам, изображенным на рис. 6.
а б Рис.6. Принципиальные блок-схемы для изучения явления резонанса в последовательном и параллельном колебательном контуре.
Напряжение синусоидальной формы поступает на последовательный (рис. 6а) либо параллельный (рис. 6б) колебательный контур. Выбор эксперимента осуществляется при выключенном генераторе (кнопка «ГЕНЕРАТОР» должна быть отжата — в противном случае появиться предупреждение) с помощью кнопки «РОД РАБОТЫ», символ * на дисплее указывает на текущее положение переключателя. Для начала эксперимента следует нажать кнопку «ENTER». Кнопки «РОД РАБОТЫ» и «ENTER»
выполняют также функцию переключения диапазонов цифрового ге-
нератора «ДИАПАЗОН». Для возвращения к меню выбора эксперимента служит кнопка «ESC». Для надежного срабатывания кнопки необходимо удерживать нажатыми в течение 1 секунды. Установка параметров контура осуществляется ручками C, L и R так же при отключенном генераторе. Текущее значение параметров отображается на ЖКД LCD индикаторе. Генератор позволяет подавать на контур переменное синусоидальное напряжение в диапазоне частот от 100 Гц до 20 кГц. Для переключения поддиапазонов используются кнопки «ДИАПАЗОН». Текущее значение частоты измеряется специальным частотомером и выводится на индикатор. Измеренное значение напряжения на конденсаторе для последовательного контура и значение тока во внешней цепи для параллельного контура измеряется чувствительными цифровыми измерительными приборами. В пределах точности измерительных приборов допускается нестабильность показаний.
28
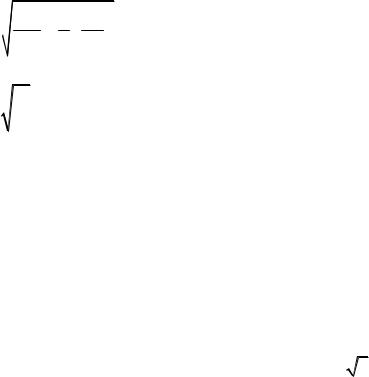
Порядок выполнения.
1.Перед началом работы ознакомится с принципиальными схемами установки, разобраться в назначении ручек и кнопок учебного модуля. Проверить целостность сетевого провода.
2.Включить установку в сеть ~220 В. Поставить переключатель «СЕТЬ» в положение «ВКЛ», при этом должен загореться сигнальный индикатор «сеть». Кнопка «ГЕНЕРАТОР» должна быть отжата, генератор выключен.
3.Пользуясь интерактивным меню, отображаемом на дисплее прибора, выбрать необходимый эксперимент (напр. «изучение резонанса в последовательном контуре»). Для перемещения по пунктам меню служит кнопка «РОД РАБОТЫ». Текущее положение отображается на дисплее символом
«*».
4.Для начала эксперимента нажать кнопку «ENTER».
5.Установить емкость, индуктивность и активное сопротивление контура с помощью соответствующих ручек на передней панели учебной установки (ручки R, L, C). Текущее значение параметров отображается на дисплее. Значение активного сопротивления катушки самоиндукции r=50 Ом, при расчетах его следует прибавлять к активному сопротивлению цепи R. Для первого эксперимента рекомендуется установить следующие значения параметров контура: L≈50 мГн; C≈13 нФ; R≈30 Ом.
6.Определить теоретическое значение резонансной частоты для напряжения на конденсаторе по формуле, легко получаемой из (15):
11 R2
рез 
LC 2 L2 ,
и теоретическое значение добротности контура по формуле:
Q |
1 |
|
L |
R |
|
C |
|
|
|
7.Включить генератор, нажав кнопку «ГЕНЕРАТОР».
8.Снять зависимость амплитуды напряжения на конденсаторе от частоты источника ЭДС (амплитудно-частотную характеристику контура) в преде-
лах приблизительно 2000 Гц от резонансной частоты. Определить шаг изменения частоты генератора, обеспечивающее достаточно детальное измерение зависимости UC0( ), особенно в области резонанса.
9.Построить резонансную кривую UC0( ). Кривая должна иметь вид, аналогичный рисунку 2.
10.Определить по графику экспериментальное значение резонансной час-
тоты, ширину графика на высоте (UСэксп0 )max / |
2 и экспериментальное |
||
значение добротности контура по формуле: |
Qэксп |
С |
. |
|
|||
|
|
|
|
29
11.Сравнить полученные экспериментальные значения величин с предварительными теоретическими расчетами.
12.Выключить генератор, отжав кнопку «ГЕНЕРАТОР».
13.Установить другое значение активного сопротивления контура (R≈200 Ом; 500 Ом; 800 Ом) и повторить пп. 6 -11.
14.Отжать кнопку «ГЕНЕРАТОР» и установить другие параметры L и С контура и повторить пп. 6-11.
15.Отжать кнопку «ГЕНЕРАТОР», выключив встроенный генератор.
16.Нажать кнопку «ESC» и выйти в меню выбора эксперимента.
17.Выбрать другой контур для изучения (второй опыт — параллельный контур).
18.Установить необходимые параметры контура (R, L, C) для проведения эксперимента. Для первого эксперимента рекомендуется установить следующие значения параметров контура: L≈50 мГн; C≈13 нФ; R≈30 Ом.
19.Рассчитать теоретически резонансную частоту контура по формуле получаемой из выражения (20):
|
эксп |
|
|
1 |
R2C |
|
рез |
0 |
L |
||||
|
|
|
||||
|
|
|
|
|
20.Включить генератор, нажав кнопку «ГЕНЕРАТОР».
21.Снять зависимость амплитуды силы тока во внешней цепи от частоты
источника ЭДС в пределах приблизительно 2000 Гц от резонансной частоты. Определить шаг изменения частоты генератора, обеспечивающее достаточно детальное измерение зависимости I( ), особенно в области резонанса.
22.Построить резонансную кривую для тока. Кривая должна иметь вид, аналогичный рисунку 5.
23.Определить по графику экспериментальное значение резонансной частоты и сравнить его с теоретическим расчетом.
24.Отжать кнопку «ГЕНЕРАТОР», выключив встроенный генератор.
25.Изменить параметры контура R, L, C и провести снятие резонансной кривой при других параметрах, повторяя пп. 19-23.
26.По окончании работы выключить установку, поставив переключатель «СЕТЬ» в положение «выкл», при этом должен погаснуть сигнальный светодиод «сеть» и вынуть сетевую вилку из розетки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.При каких условиях возникает резонанс в электрическом колебательном контуре?
2.От чего зависит амплитуда силы тока в электрическом колебательном контуре при резонансе?
3.Могут ли возникнуть колебания в контуре, состоящем из сопротивления и конденсатора (сопротивления и индуктивности)?
30