Тест №4.

1. Из следующих предложений выберете предикаты:

а) ;

б) "Для выполняется равенство";

в) Все числа, делящиеся на 9, делятся на 3;

г) Неверно, что 17 делится на 5.

2. Найдите множество истинности предиката : "".

а) 2;

б) ;

в) ;

г) .

3. Даны предикаты : "Числохделится на 3" и: "Сумма цифр числа делится на 9". Установите, какие из следующих импликаций истинны для всех натуральных чисел:

а) ;

б) ;

в) ;

г) .

4. Задайте множество значений переменной так, чтобы на этом множестве второй предикат следовал из первого. : "";: "".

а) ;

б) ;

в) ;

г) .

5. Задайте множество значений переменной так, чтобы предикат

: "" и: "" были на этом множестве эквивалентны.

а) ;

б) ;

в) .

6. Какой логический знак нужно вставить, чтобы выполнялась равносильность ?

а) ;

б) ;

в) ;

г) .

7. Задан предикат : "Рекавпадает в море". Выбрать из следующих предикатов предикат: "Существует море, в которое впадает река".

а) ;

б) ;

в) ;

г) .

8. Для формулы найти равносильную приведенную форму:

а) ;

б) ;

в) ;

г) .

9. Применяя равносильные преобразования, приведите следующие формулы к приведенной нормальной форме :

а) ;

б) ;

в) ;

г) .

Лекция 5. Применение языка логики предметов для записи математических предложений. П. 5.1. Запись математических определений.

Язык логики предикатов очень удобен для записи математических предложений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства.

Рассмотрим несколько примеров.

1. Определение четной функции.

Функция называетсячетной, если область ее определения симметрична относительно начала координат и для каждогоxиз области определения выполняется равенство.

Это определение можно записать:

2. Определение экстремума функции(минимум в точке).

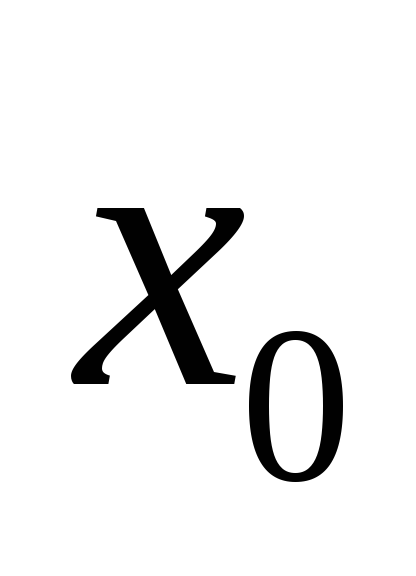где

П. 5.2. Формулировка математических теорий.

Большинство математических теорий формулируются так: на некотором множестве Миз предикатаА(х)следуетВ(х). Также теорема состоит из трех частей: описание множестваМ, к элементам которого эта теорема относится, условия теоремыА(х)иВ(х)- заключение теоремы.

Примеры:

1) В теореме: «Если диагонали параллелограмма равны, то он является прямоугольником», М– множество всех параллелограммовА(х)– «Диагонали параллелограммахравны» иВ(х) – «Параллелограммхявляется прямо-угольником».

2) В теореме: «Если последняя цифра натурального числа хравно 0 или 5, то это число делится на 5».

М– множество натуральных чисел,

: «Последняя цифра числахравно 5»,

: « Последняя цифра числахравно 0»,

В(х): « Числохделится на 5».

Развернутая запись такова

П. 5.3. Построение противоположных утверждений и доказательство методом от противного.

Если задано утверждение А, то построитьможно с помощью равносильных преобразований. Иногда это, приводит к тому, чтодает негативное (неконструктивное) определение.

Пример:

1) Определение бесконечно малой функции.

«Функция называется бесконечно малой при, если».

Это определение запишем на язык :

где – трехместный предикат, определяющий условие предельного периода.

Найдем его отрицание:

Это негативное определение. Оно подойдет для формирования контрпримера для того, чтобы доказать, что – не бесконечно малая величина в точкеа.

Позитивное определение бесконечно большой величины такое:

2) Рассмотрим построение утверждения, отрицающего справедливость некоторой теоремы: .

. Следовательно, чтобы доказать, что теорема неверна, достаточно указать такой элемент, для которогоистинно, аложно, то есть привести контрпример.

Пример: Рассмотрим утверждение: «Если функция непрерывна в точке, то она и дифференцируема в этой точке».

Пусть М– множество всех функций, определенных в точке,-предикат, выражающий свойство функции быть непрерывной, а- свойство быть дифференцируемой в точке в точке. То теорема имеет вид.

Противоположное утверждение , то есть найдется функция, определенная в точке, которая непрерывна, но не имеет производной в. Простейшая из всех таких функций.

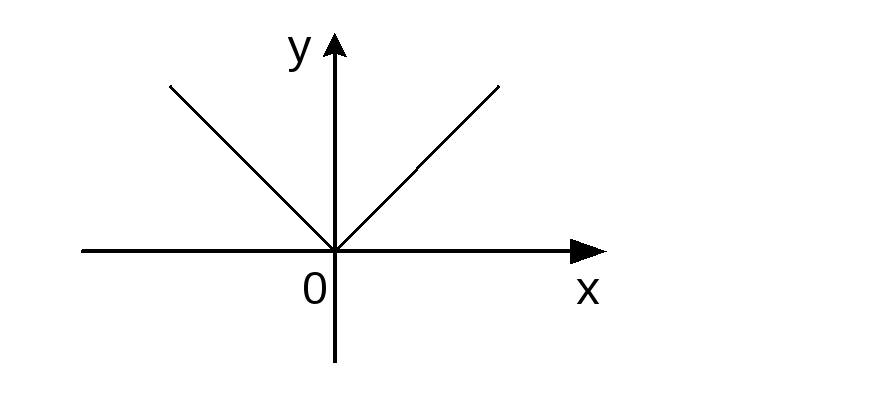
Схема доказательства от противного очень похожа на только что рассмотренный пример: предполагается, что теорема неверна, т.е. истинно противоположное утверждение.

Если из последней формулы путем логический рассуждений приходят к неверному утверждению, то делается вывод о том, что исходная теорема верна.