
- •Методы математического моделирования и вычислительной математики Никитина т.П. Оглавление
- •Введение
- •Основы моделирования
- •Классификация математических моделей
- •Основные этапы математического моделирования
- •Математические модели аналитического типа
- •Эмпирические математические модели
- •Методы вычислительной математики
- •Постановка задачи
- •Этапы решения задачи
- •Локализация корня
- •Метод половинного деления
- •Метод хорд
- •Метод касательных (Метод Ньютона)
- •Комбинированный метод хорд и касательных
- •Решение систем линейных уравнений (слау)
- •Приближенные методы решения систем линейных уравнений Метод простой итерации ( Метод Якоби)
- •Метод Гаусса - Зейделя
- •1. Использованием обратной матрицы
- •2. Решение системы уравнений методом Гаусса
- •Интерполяция
- •Постановка задачи
- •Полиномиальная (алгебраическая) интерполяция
- •Интерполяция по Лагранжу
- •Вычисление определенных интегралов вида Постановка задачи
- •Метод прямоугольников
- •Метод трапеций
- •Метод Симпсона (метод парабол)
- •Решение обыкновенных дифференциальных уравнений Постановка задачи
- •Численные методы решения задачи Коши оду первого порядка
- •Метод Эйлера
- •Усовершенствованный метод Эйлера. Метод Гюна.
- •Методы прогноза и коррекции
- •Метод Рунге-Кутта
- •Решение задачи оптимизации
- •Постановка задачи
- •Численные методы решения задачи одномерной оптимизации
- •Этапы решения задачи
- •Метод двойного половинного деления
- •Метод золотого сечения
- •Численные методы решения задачи линейного программирования
- •Постановка задачи
- •Реализация симплекс метода
- •Литература
Вычисление определенных интегралов вида Постановка задачи
Пусть требуется вычислить определенный
интеграл ![]() ,
гдеf(x) – непрерывная на отрезке [a;
b] функция.
,
гдеf(x) – непрерывная на отрезке [a;
b] функция.
Вычислить определенный интеграл можно с помощью аналитической формулы:
![]() – формула Ньютона-Лейбница.
– формула Ньютона-Лейбница.
Однако во многих случаях не удается преобразовать f(x) к табличной функции, для которой известна аналитическая формулаF(x). В таких случаях приходится решать задачу численного интегрирования.
Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитическом виде, некоторой простой табличной функциейφ(x). Поскольку в этом случае решение является приближенным, то в постановке задачи необходимо задавать точность.
Обзор методов численного интегрирования
Методы вычисления однократных интегралов называются квадратурными(для кратных интегралов –кубатурными).
К квадратурным методам относятся методы Ньютона-Котеса.В этих методахφ(x)– это полиномы различных степеней, к ним относятся: метод прямоугольников, метод трапеций, метод Симпсона.
Метод прямоугольников
Постановка задачи
Дан определенный интеграл ![]() ,
гдеf(x)– функция непрерывная на
отрезке [a; b] и точность– малое положительное число. Необходимо
вычислить интеграл с заданной точностью.
,
гдеf(x)– функция непрерывная на
отрезке [a; b] и точность– малое положительное число. Необходимо
вычислить интеграл с заданной точностью.
Графическая интерпретация метода
С геометрической точки зрения интеграл при f(x) > 0 равен площади криволинейной трапеции, ограниченной кривойy = f(x), осьюOx и прямымиx = a,x = b. Разобьем отрезок [a; b] наnравных частей:x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n.Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямыхx=xi. Заменим при вычислении площади каждую «маленькую» криволинейную трапецию прямоугольником, то есть заменим кривуюf(x) полиномом нулевой степени – отрезком, параллельным оси абсцисс. При этом прямоугольники можно построить тремя разными способами, взяв за одну из сторон прямоугольника ординату xi-1, или xi, или (xi-1+xi)/2. Таким образом, различают методы левых, правых и средних прямоугольников.
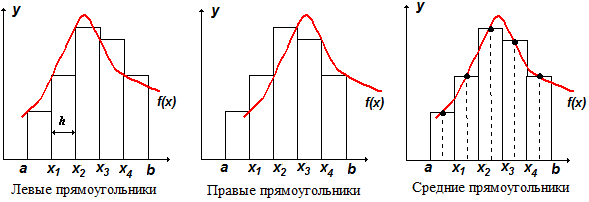
Алгоритм метода прямоугольников
Вводим исходные значения ,a,b.
Задаем n=1,S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:
Метод прямоугольников с недостатком (левые прямоугольники).
Приближенное значение интеграла равно сумме площадей прямоугольников:
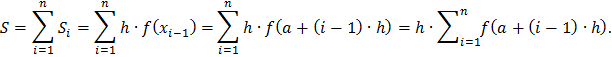
Метод прямоугольников с избытком (правые прямоугольники).
Приближенное значение интеграла равно сумме площадей прямоугольников:
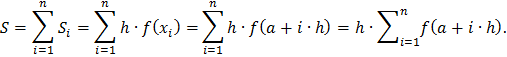
Метод средних прямоугольников.
Приближенное значение интеграла равно сумме площадей прямоугольников:
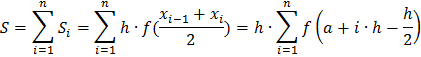
Проверка условия |S0-S|<= ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить ![]() dxс точностью=0,001.
dxс точностью=0,001.
Заполнение клеток листа MS Excel для n=2:
|
Адрес клетки |
Содержание |
Тип |
|
A1 |
n=2 |
Текст |
|
C1 |
a= |
Текст |
|
D1 |
0 |
Число |
|
E1 |
b= |
Текст |
|
F1 |
0,5 |
Число |
|
B2 |
h= |
Текст |
|
C2 |
=(F1-D1)/2 |
Формула |
|
A4 |
x |
Текст |
|
B4 |
xcp |
Текст |
|
C4 |
f левые прямоугольники |
Текст |
|
D4 |
f правые прямоугольники |
Текст |
|
E4 |
f средние прямоугольники |
Текст |
|
A5 |
=D1 |
Формула |
|
B5 |
=(A5+A6)/2 |
Формула |
|
C5 |
=EXP(-A5*A5/2) |
Формула |
|
D5 |
=EXP(-A6*A6/2) |
Формула |
|
E5 |
=EXP(-B5*B5/2) |
Формула |
|
A6 |
=A5+$C$2 |
Формула |
|
B6 |
=(A6+A7)/2 |
Формула |
|
C6 |
=EXP(-A6*A6/2) |
Формула |
|
D6 |
=EXP(-A7*A7/2) |
Формула |
|
E6 |
=EXP(-B6*B6/2) |
Формула |
|
B6 |
Результат |
Текст |
|
C6 |
=СУММ(C5:C6)*$C$2 |
Формула |
|
D6 |
=СУММ(D5:D6)*$C$2 |
Формула |
|
E6 |
=СУММ(E5:E6)*$C$2 |
Формула |
Вид листа MS Excel:
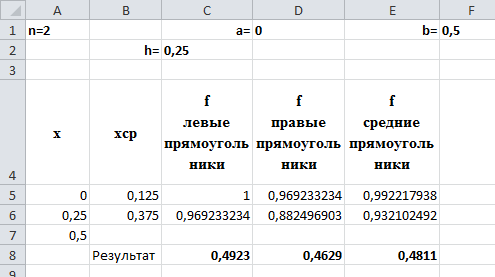
Результаты расчета для n=2:
по методу левых прямоугольников 0,4923;
по методу правых прямоугольников 0,4629;
по методу средних прямоугольников 0,4811.
Заполнение клеток листа MS Excel для n=4:
|
Адрес клетки |
Содержание |
Тип |
|
H1 |
n=4 |
Текст |
|
J1 |
a= |
Текст |
|
K1 |
0 |
Число |
|
L1 |
b= |
Текст |
|
M1 |
0,5 |
Число |
|
I2 |
h= |
Текст |
|
J2 |
=(M1-K1)/4 |
Формула |
|
H4 |
x |
Текст |
|
I4 |
xcp |
Текст |
|
J4 |
f левые прямоугольники |
Текст |
|
K4 |
f правые прямоугольники |
Текст |
|
L4 |
f средние прямоугольники |
Текст |
|
H5 |
=K1 |
Формула |
|
I5 |
=(H5+H6)/2 |
Формула |
|
J5 |
=EXP(-H5*H5/2) |
Формула |
|
K5 |
=EXP(-H6*H6/2) |
Формула |
|
L5 |
=EXP(-I5*I5/2) |
Формула |
|
I6:L8 |
автозаполнение формулами диапазона I5:L5 |
Формула |
|
H6 |
=H5+$J$2 |
Формула |
|
H7:H8 |
автозаполнение формулой из H6 |
Формула |
|
I10 |
Результат |
Формула |
|
J5 |
=СУММ(J5:J8)*$J$2 |
Формула |
|
K5 |
=СУММ(K5:K8)*$J$2 |
Формула |
|
L5 |
=СУММ(L5:L8)*$J$2 |
Формула |
Вид листа MS Excel:
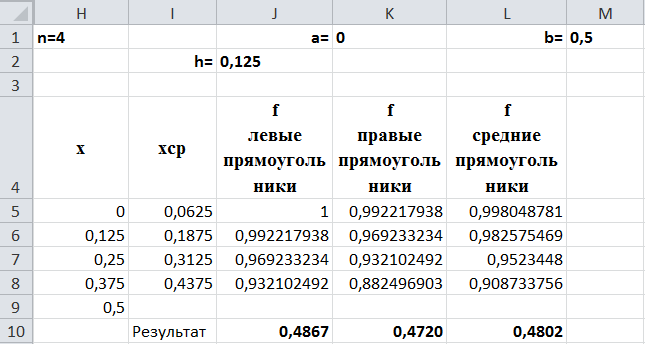
Результаты расчета для n=4:
по методу левых прямоугольников 0,4867;
по методу левых прямоугольников 0,4720;
по методу левых прямоугольников 0,4802.
Далее выполняем расчеты для n=8,16,32.
Вид листа MS Excel для n=8:
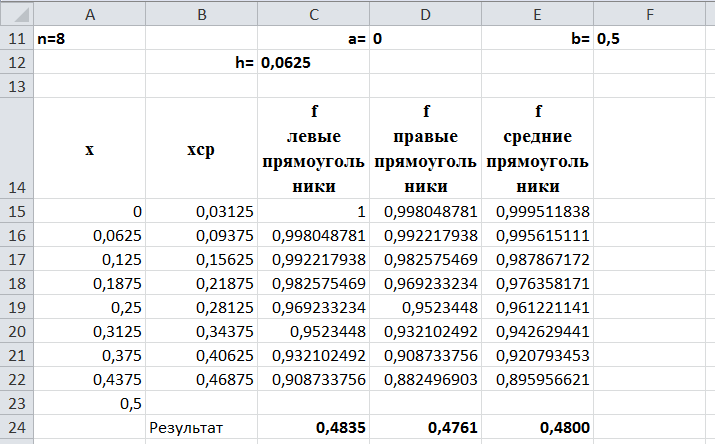
Результаты расчета для n=8:
по методу левых прямоугольников 0,4835;
по методу правых прямоугольников 0,4761;
по методу средних прямоугольников 0,4800.
Вид листа MS Excel для n=16:
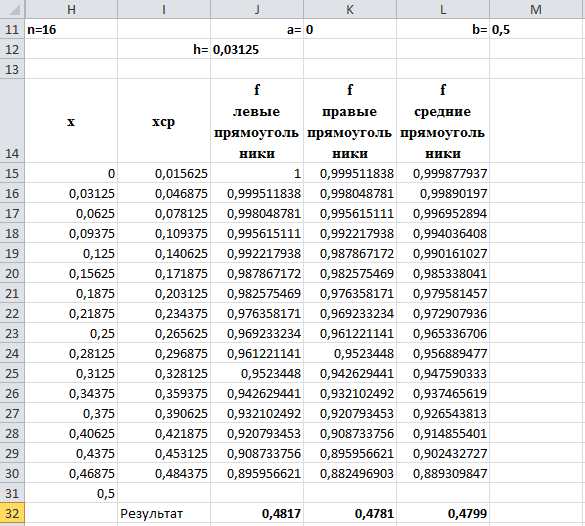
Результаты расчета для n=16:
по методу левых прямоугольников 0,4817;
по методу правых прямоугольников 0,4781;
по методу средних прямоугольников 0,4799.
Вид листа MS Excel для n=32:
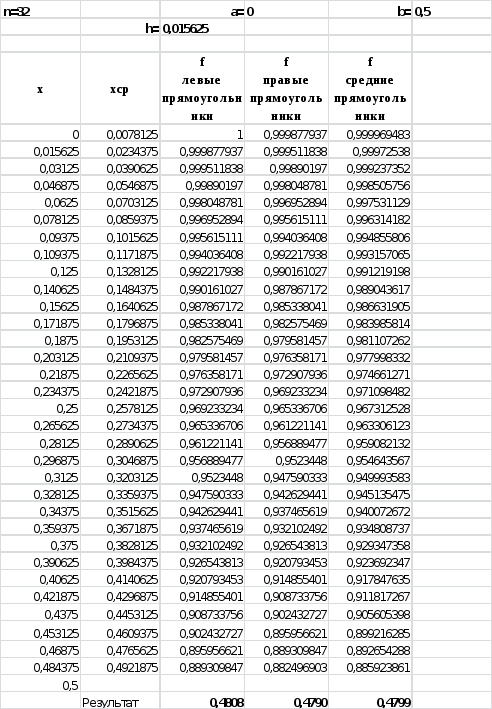
Результаты расчета для n=32:
по методу левых прямоугольников 0,4808;
по методу правых прямоугольников 0,4790;
по методу средних прямоугольников 0,4799.
Вид таблицы результатов:
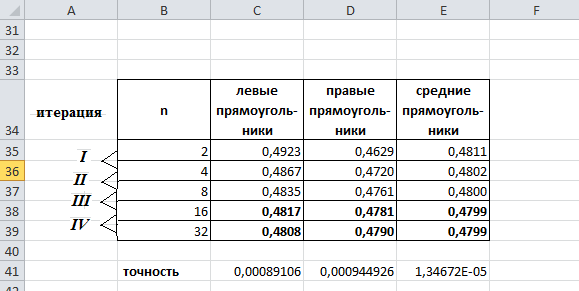
Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута на четвертой итерации для методов левые и правые прямоугольники и второй итерации для метода средние прямоугольники.
