
Информатика (2 курс)
.pdfМетодические указания для выполнения лабораторных работ по теме |
|
|
|
Математика в «Excel» |
|
|
Оглавление |
|
Раздел 1. Аналитическая геометрия и линейная алгебра.................................................................................................... |
2 |
|
Тема 1.1 Декартова система координат ............................................................................................................................ |
2 |
|
Тема 1.2 Кривые второго порядка на плоскости.............................................................................................................. |
3 |
|
Тема 1.3 |
Графическое решение системы уравнений. ...................................................................................................... |
3 |
Тема 1.4 |
Использование программы Excel в линейной алгебре..................................................................................... |
4 |
Раздел 2. Элементы математического анализа..................................................................................................................... |
5 |
|
Тема 2.1. Определенный интеграл..................................................................................................................................... |
5 |
|
Раздел 3. Задачи оптимизации............................................................................................................................................... |
7 |
|
Тема 3.1 |
Решение уравнения с одним неизвестным........................................................................................................ |
7 |
Тема 3.2 |
Аппроксимация экспериментальных данных................................................................................................... |
8 |
1
Раздел 1. Аналитическая геометрия и линейная алгебра
Тема 1.1 Декартова система координат
Самая простая и наиболее распространенная система координат на плоскости называется декартовой по имени из-
вестного математика и философа Рене Декарта. Декартова система координат образована двумя перпендику-
лярными осями, осью Х и осью Y.
Точка пересечения осей называется началом и служит одновременно началом координат на каждой из осей. Масштаб на осях выбирается одинаковый (иначе система координат будет называться аффинной, а не декартовой).
Прямая линия на плоскости
Уравнением линии на плоскости x0y может записываться по разному:
1.Уравнение прямой с угловым коэффициентом y=kx+b, где k=tg – угловой коэффициент прямой, – угол наклона прямой к оси x, b – ордината точки пересечения прямой с осью y.
2. Уравнение прямой, проходящей через две данные точки (x1, y1), (x2, y2): |
y y2 |
|
x x2 |
. |
||||
y |
y |
2 |
x |
x |
2 |
|||
|
1 |
|
1 |
|
|
|||
3.Общее уравнение прямой Ax+By+C=0.
Всегда важно указать, какие значения может принимать независимая переменная х. Собственно говоря,
символом х обозначается произвольный элемент некоторого числового множества, которое называется областью определения функции.
С помощью системы координат мы можем каждую функцию изобразить наглядно, в виде графика.
В программе Excel для построения прямых, а также кривых, может быть использован специальный инструмент – Мастер диаграмм, который дает возможность строить различные типы графиков. Для применения Мастера диаграмм необходимо ввести точки прямой линии в рабочую таблицу, вызвать Мастер диаграмм, задать тип диаграммы, диапазоны данных и подписей оси x, ввести название осей.
Пример.
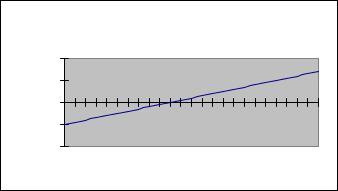
Рассмотрим построение прямой в Excel на примере уравнения y=2x+1 на интервале x 3, 3 с шагом =0,5.
Для решения задачи на чистый лист Excel занести значения аргумента и подсчитать значение функции. В ячейку A1 введите слово Аргумент , в ячейку B1 – слово Прямая. В ячейку А2 введите левую границу диапазона «-3». В ячейку А3 – «-2,5». Выделите блок ячеек А2:А3 и при помощи маркера заполнения протяните и заполните весь диапазон изменения аргумента. В ячейку В2 введите формулу =2*А2 + 1 (ссылку на ячейку можно заполнить при помощи щелчка на соответствующей ячейке). Затем с использованием маркера заполнения копируем эту формулу в весь диапазон. На Панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В по-
явившемся диалоговом окне указать в правом поле тип диаграммы График и подтип диаграммы в правом поле – График с маркерами. После чего нажимаем в диалоговом окне кнопку Далее.
Впоявившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо вы-
брать вкладку Диапазон данных и в поле Диапазон указать интервал данных, т.е. ввести ссылку на ячейки, содержащие данные, необходимые для представления на диаграмме (при помощи мышки выделить диапазон В1:В14.
Врабочем поле должна появиться надпись Лист1!$B$1:$B$14. Ряды в столбцах. Если диалоговое окно закрывает столбцы с данными, его можно отодвинуть, потянув за строку заголовка указателем мыши. Во вкладке Ряд этого же диалогового окна необходимо указать Подписи по оси Х. Для этого, поставив курсор в поле мышкой отметьте диапазон аргумента (Лист1!$A$2:$A$14). Нажмите кнопку Далее. В третьем окне Мастера диаграмм (шаг 3 из 4): параметры диаграммы нужно ввести заголовок диаграммы (если его нет) и название осей (во вкладке Заголовки). Во вкладке Легенда щелчком мыши установить флажок в поле добавить легенду. После чего нажать Далее. В четвертом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо указать место расположения диаграммы (на отдельном или текущем листе). Если диаграмма в демонстрационном поле имеет нужный вид, нажать кнопку Готово. В противном случае нажать кнопку Назад и изменить установки.
|
|
|
Функция y=2*x+1 |
|
|
||||
|
10 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
-53 |
-2,25 |
-1,5 |
,75 |
0 |
0,75 |
1,5 |
2,25 |
3 |
|
- |
|
|
||||||
|
|
0 |
|
|
|||||
|
-10 |
|
- |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2
Тема 1.2 Кривые второго порядка на плоскости
К кривым второго порядка относятся парабола, гипербола, окружность, эллипс.
Параболой называется множество точек, расстояние от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны. Общий вид уравнения параболы: Cy 2 Dx Ee F 0
В Excel построение параболы осуществляется аналогично построению прямой. При этом уравнение должно быть предварительно приведено к виду y=f(x).
Пример.
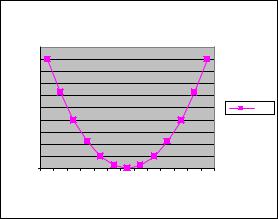
Построить параболу y=x2 в диапазоне х[-3;3] с шагом 0,5.
Решение.
Пусть открыть чистый рабочий лист, иначе добавить рабочий лист. По аналогии с предыдущим примером заполните исходные данные. Вызовите Мастер диаграмм. Постройте график функции y=x2.
|
|
|
график параболы |
|
|||
|
10 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
у |
5 |
|
|
|
|
|
y=x2 |
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
2 |
1 |
0 |
1 |
2 |
3 |
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
х |
|
|
Тема 1.3 Графическое решение системы уравнений.
Системы уравнений с двумя неизвестными могут быть приближенно решены графически. Их решением являются координаты точки пересечения линий, соответствующих уравнениям системы. При этом точность решения будет определяться величиной шага дискретизации (чем шаг меньше, тем точность выше). Рассмотрим примеры графического решения системы двух уравнений.
Пример.
Пусть необходимо найти решение системы y sin x
y cosx
в диапазоне x 0;3 с шагом =0,2.
Решение.
Ввести данные в рабочую таблицу. В ячейку А1 ввести слово Аргумент. Начиная с ячейки А2 в столбец ввести значения х. В ячейку В1 ввести слово Синус. Далее в ячейку В2 для получения значения синуса воспользуемся специальной функцией (Вставка - Функция). В появившемся диалоговом окне Мастера функций – шаг 1 из 2 в поле Категория выбираем Математические. Выбираем функцию SIN. Нажимаем кнопку ОК. Появляется диалоговое окно функции SIN. Указываем значение аргумента при помощи щелчка на ячейке А2. Нажимаем ОК. В ячейке В2 появилось значение функции. Теперь при помощи Маркера заполнения «размножим» функцию, находящуюся в ячейке В2. Аналогично получаем значение косинуса. Далее необходимо построить диаграмму кривых синуса и косинуса. Как видно из диаграммы система имеет одно решение (есть точка пересечения), и оно на заданном интервале единственное. Таким образом, решением системы в заданном диапазоне являются координаты точки пересечения кривых. Для их нахождения необходимо навести указатель мыши на точку пересечения и щелкнуть левой
кнопкой мыши. Появляется надпись с указанием искомых координат. 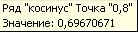 . Таким образом приближенное решение системы х=0,8, у=0,697.
. Таким образом приближенное решение системы х=0,8, у=0,697.
Упражнения.
1.Построить прямую 3x+2y-4=0 в диапазоне x 1; 3 с шагом =0,25.
2.Построить прямую, проходящую через точки А(0;3) и B(2;2) в диапазоне x 1; 4 с шагом =0,5.
3.Построить прямую, проходящую через точки начало координат и точку B(2;3) в диапазоне x 1; 4 с ша-
гом =0,25.
4.Построить параболу y=2x2-1 в диапазоне х[0;4] с шагом 0,25.
y 2x 1 |
в диапазоне x 0,2; 3 с шагом =0,2. |
5. Графически решить систему |
|
y ln x |
|
3

|
2 |
|
в диапазоне x 0,2; 3 с шагом =0,2. |
|
6. Графически решить систему y |
|
|
||
x |
||||
|
|
|||
|
|
|
|
|
y 2x |
|
|||
Тема 1.4 Использование программы Excel в линейной алгебре
Цель занятия: Научиться производить операции с матрицами в Excel.
Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойной индексацией:
aij , где i – номер строки, j – номер столбца. Например,
a |
a |
a |
|
|
|
11 |
12 |
1n |
|
a21 |
a22 |
a2n |
(aij ) |
|
А |
|
|
|
|
|
|
|
|
|
|
|
am2 |
|
|
am1 |
amn |
|
||
Операции с матрицами.
Транспонирование
Транспонированной (обратной) называется матрица, в которой столбцы исходной матрицы заменяются строками с
соответствующими номерами. Исходная матрица: А = (аij), транспонированная – А |
т |
= ( аji). |
|||||||||||
|
|||||||||||||
3 |
7 |
11 |
|
|
3 |
18 |
5 |
|
|
||||
|
18 |
19 |
39 |
|
А |
t |
|
7 |
19 |
91 |
|
|
|
А |
|
|
|
|
|
|
|||||||
|
5 |
91 |
87 |
|
|
|
|
11 |
39 |
87 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Для осуществления транспонирования в Excel используется функция ТРАНСП в категории Ссылки и массивы, которая позволяет менять ориентацию массива. Функция имеет вид ТРАНСП(массив). Массив – это диапазон ячеек на рабочем листе, в котором записаны элементы матрицы.
Пример 1. Дана матрица А, получить транспонированную матрицу Ат.
1 |
2 |
3 |
4 |
5 |
||
А |
|
|
|
|
|
|
|
6 |
7 |
8 |
9 |
0 |
|
|
|
|||||
Решение.
1.Введите на рабочий лист Excel предложенную матрицу (в ячейку число). Выделите указателем мыши блок ячеек под транспонированную матрицу (размер транспонированной матрицы: количество строк = количеству столбцов в исходной матрице). В данном случае размер исходной матрицы 2*5, транспонированной – 5*2 .
2.Меню Вставка – Функция, в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, в рабочем поле функции – имя функции ТРАНСП.
3.В окне ТРАНСП укажите диапазон ячеек исходной матрицы. После чего нажмите сочетание клавиш
CTRL+SHIFT+ENTER.
4.В указанном вами диапазоне должна появиться транспонированная матрица.
Вычисление определителя матрицы.
Важной характеристикой квадратных матриц является их определитель. Определитель матрицы – это число, вычисляемое на основе значений элементов массива. Определить матрицы обозначается как À или . Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по
а |
а |
а21 а22 а11а22 а12а21.
ВExcel для вычисления определителя матрицы используют функцию МОПРЕД в категории Математические. Функция имеет вид МОПРЕД (массив). Здесь массив – это числовой массив, в котором хранится матрица с равным количеством строк и столбцов.
Пример 2.
|
1 |
2 |
3 |
|
Найти определитель матрицы |
|
0 |
2 |
|
А |
3 |
|||
|
|
1 |
0 |
|
|
|
3 |
||
Решение.
1.На лист рабочей книги введите исходные данные в ячейки А1:С3.
2.Поставьте табличный курсор в ячейку А4.
3.Меню Вставка – Функция. В поле Категория выберите Математические, в рабочем поле Функция – имя функции МОПРЕД. Нажмите ОК.
4.В появившееся диалоговое окно МОПРЕД введите диапазон исходной матрицы. Нажмите ОК.
4
5.В ячейке А4 появится значение определителя (6).
Умножение матриц.
Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй. Для нахождения произведения двух матриц в Excel используется функция МУМНОЖ, которая вычисляет произведение матриц (матрицы хранятся в массивах). Функция имеет вид МУМНОЖ(массив1; массив 2). Здесь массив 1 и массив 2 – это перемножаемые матрицы. При этом количество столбцов аргумента массив 1 должно быть таким же, как количество строк аргумента массив 2, оба массива должны содержать только числа. Результатом
(т.е. матрицей-произведением) является массив с таким же числом строк, как массив 1, и таким же числом столбцов, как массив 2.
Пример 3.
|
1 |
3 |
4 |
2 |
|
|
1 |
3 |
|
||
Найти произведение массивов |
и |
|
2 |
2 |
|
||||||
|
3 2 0 |
|
|
|
|
||||||
|
А |
1 |
|
В |
|
|
|
||||
|
|
0 |
1 |
1 |
2 |
|
|
10 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
||
Решение:
1.Введите матрицу А в диапазон А1:D3, а матрицу В в диапазон А4:В7.
2.Выделите блок ячеек под результирующую матрицу. Для этого необходимо найти размер матрицыпроизведения. Ее размерность будет в данном примере 3*2. Выделите блок ячеек F1:G3.
3.Вызовите Мастер функций. В поле Категория выберите Математические, в поле Функции – имя функции МУМНОЖ. Нажмите ОК.
В появившемся диалоговом окне введите диапазоны массива 1 и массива 2 (соответственно А1:D3 и А4:В7). После этого нажмите сочетание клавиш CTRL+SHIFT+ENTER.
4.После этого в выделенном вами диапазоне должна появится матрица, которая равна произведению исходных матриц.
Упражнения.
|
2 |
3 |
5 |
||||
1. Найдите матрицу, обратную данной и определитель исходной матрицы. |
|
4 |
1 |
3 |
|
||
А |
|
||||||
|
|
7 |
2 |
0 |
|
||
|
|
|
|||||
2. Найдите матрицу, обратную данной и определитель исходной матрицы |
2 |
3 |
1 |
||||
|
4 |
1 |
5 |
|
|||
|
А |
|
|||||
|
|
1 |
2 |
4 |
|
||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
|
3. |
Найти произведение матриц А*В, где А 1 2 |
3 , |
|
5 |
|
||||||
В |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
1 |
2 |
|
|
|
|
|
|
|||
4. |
0 |
2 |
4 |
|
|
|
|
||||
Вычислите А*В = |
3 |
4 |
|
|
|
|
|
||||
|
|
|
* |
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
||
|
|
5 |
6 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Раздел 2. Элементы математического анализа
К математическому анализу относят совокупность разделов математики, посвященных исследованию функций метолами дифференциального и интегрального исчислений.
Производной функции y f (x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
y lim |
y |
lim |
f (x x) f (x) |
|
x |
x |
|||
x 0 |
x 0 |
Геометрический смысл производной заключается в том, что производная f (x0 ) есть угловой коэффициент каса-
тельной, проведенной к кривой y f (x) в точке х0.
Обычно производная характеризует скорость изменения функции. Например, скорость движения – это производная от пути по времени st .
Продифференцировать функцию – это значит найти ее производную (можно использовать таблицы производных).
Тема 2.1. Определенный интеграл
5

Пусть на отрезке [a,b] задана функция y f (x), и отрезок разбит на n элементарных отрезков точками x0, x1, …,
xn: a= x0 < x1 <…< xn=b, x=xi-x i-1/
Определенным интегралом от функции y f (x) не отрезке [a,b] называется предел интегральной функции приx 0, а функция f(x) называется интегрируемой на отрезке [a,b].
b |
f (x)dx lim |
n |
f (x) x |
a |
x 0 |
i 1 |
|
Число a называется нижним пределом интегрирования, а число b – его верхним пределом.
Геометрический смысл определенного интеграла заключается в следующем. Если функция y f (x) неотрица-
тельна на отрезке [a,b], где a<b, то b |
f (x)dx численно равен площади под кривой |
y f (x) на [a,b]. Для нахож- |
a |
|
|
дения определенного интеграла пользуются формулой Ньютона-Лейбница:
b |
f (x)dx F (b) F (a), |
(1) |
a |
|
|
где F(a) и F(b) первообразные для f(x) в точках a и b. Первообразной функцией для функции y f (x) на промежутке Х называется функция F(x), если в каждой точке x этого промежутка F (x) f (x).
Однако применение формулы Ньютона-Лейбница на практике связано с трудностями, поэтому используют численные методы, позволяющие найти приближенное значение искомого интеграла. Рассмотрим два метода:
-метод прямоугольников – как суммы элементарных прямоугольников
|
b |
|
|
|
- |
f (x)dx n |
f (xi ) x |
(2) |
|
|
a |
i 1 |
|
|
Суть метода прямоугольников в том, что на каждом из участков разбиения [xi-1, xi] участок кривой y f (x) заменяется отрезком прямой, параллельным оси абсцисс. Тогда определенный интеграл приближенно равен сумме
b
площадей прямоугольников на каждом участке разбиения. f (x)dx S1 S2 ... Sn
a
-метод трапеций – как суммы элементарных трапеций
|
b |
n 1 |
f (x0 ) f (xn ) |
|
|
|
- |
f (x)dx ( f (xi ) |
) x |
(3) |
|||
2 |
||||||
|
a |
i 1 |
|
|
||
метод трапеций является более точным, т.к. каждый участок кривой заменяется не прямыми, а хордами, стягивающими концевые точки. Тогда каждое слагаемой интегральной суммы будет равно площади трапеции с основаниями f(xi) и f(xi-1) и высотой х.
3
Пример. Методом прямоугольника и методом трапеции найти x2dx с шагом х=0,1. Заметом, что этот интеграл
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
x |
3 |
|
3 9 0 9 |
|
|
|
|
|
|||||
|
|
легко вычислить аналитически: x2dx |
|
|
||||
аргумент |
функция |
|
|
|
||||
|
|
|||||||
|
|
|
3 |
|
0 |
|||
0 |
0 |
0 |
|
|||||
0,1 |
0,01 |
|
|
|||||
Решение1 . |
|
|
|
|
|
|||
0,2 |
0,04 |
|
|
|
|
|
||
0,3 |
0,09 |
На листе Excel составляем таблицу данных. Заполняем значение аргумента (в ячейки |
||||||
0,4 |
0,16 |
|||||||
А1:А32) и значение функции ( x2 ) (в ячейки В1:В32) (см. Декартова система координат, |
||||||||
0,5 |
0,25 |
|||||||
0,6 |
0,36 |
Пример 1). |
|
|
|
|
|
|
0,7 |
0,49 |
|
|
|
|
|
||
0,8 |
0,64 |
|
|
|
|
|
|
|
0,9 |
0,81 |
Введем слово интеграл в ячейку А33 и в соседней ячейке формулы =0,1*, затем вызываем |
||||||
1 |
1 |
|||||||
|
|
Мастер функций и в категории Математические выбираем функцию СУММ. Нажима- |
||||||
1,1 |
1,21 |
|||||||
1,2 |
1,44 |
ем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – значения |
||||||
1,3 |
1,69 |
|||||||
функции (В2:В32). В ячейке В33 появляется приближенное значение интеграла (9,455). |
||||||||
1,4 |
1,96 |
|||||||
1,5 |
2,25 |
Ошибка в методе прямоугольников составила 0,455. |
||||||
1,6 |
2,56 |
|||||||
Решение 2. |
|
|
|
|
|
|||
1,7 |
2,89 |
|
|
|
|
|
||
1,8 |
3,24 |
Используем метод трапеции. Для этого в ячейку А34 введем слово интеграл 2. В сосед- |
||||||
1,9 |
3,61 |
нюю ячейку вводим формулу =0,1*((В2+В32)/2+ ) затем вызываем функцию СУММ. |
||||||
2 |
4 |
|||||||
|
|
Нажимаем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – |
||||||
2,1 |
4,41 |
|||||||
2,2 |
4,84 |
значения функции (В3:В31). В ячейке В34 появляется значение =9,005. В данном случае |
||||||
2,3 |
5,29 |
|||||||
ошибка метода составляет 0,005, что вполне приемлемо. |
||||||||
2,4 |
5,76 |
|||||||
2,5 |
6,25 |
|
|
|
|
|
|
|
2,6 |
6,76 |
|
|
|
|
|
|
|
2,7 |
7,29 |
|
|
|
|
6 |
||
2,8 |
7,84 |
|
|
|
|
|||
|
|
|
|
|
|
|||
2,9 |
8,41 |
|
|
|
|
|
|
|
3 |
9 |
|
|
|
|
|
|
|
Интеграл |
9,455 |
|
|
|
|
|
|
|
интеграл 2 |
9,005 |
|
|
|
|
|
|
|

Упражнения.
Найти при помощи метода прямоугольника и трапеции определенные интегралы:
3.1
1. sin xdx с шагом х=0,1.
0
2
2. xdx с шагом х=0,1.
0
1.51
3.x dx с шагом х=0,1.
1
Раздел 3. Задачи оптимизации.
Очень широкий класс задач составляют задачи оптимизации. Наиболее типовыми задачами оптимизации являются следующие: решение уравнения с одним неизвестным, задачи линейного программирования и аппроксимация функции.
Тема 3.1 Решение уравнения с одним неизвестным
Одним из приложений задач оптимизации является численное решение уравнения вида f(x)=0. Для решения подобных уравнений в программе Excel; используется удобный и простой инструмент Подбор параметров. Процесс решения распадается на два этапа:
1.Задание на рабочем листе ячейки, содержащей переменную решаемого уравнения (влияющую ячейку), и ячейки, содержащей формулу уравнения ( зависящей или целевой ячейки).
2.Ввод адресов влияющей и целевой ячеек в диалоговом окне Подбор параметра и получение ответа (или сообщение и его отсутствии).
Пример 1. Найти решение уравнения lnx=0.
Решение. Этап 1.
1.В ячейку А1 вводим – корень, в ячейку В1 – функция.
2.В ячейку А2 вводим ориентировочное значение корня, например, 3.
3.Заносим в ячейку В2 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку А2. В ячейке В2 появляется число 1,098612.
Этап 2.
1. Вызываем процедуру Подбор параметров (Сервис – Подбор параметра).
2.В поле Установить в ячейке мышью указываем В2, в поле Значение с клавиатуры задаем 0 (правая часть уравнения), в поле Изменяя значение ячейки мышью указываем А2 (см. рис).
3.Щелкаем на кнопке ОК и получаем результат подбора, отображаемый в диалоговом окне Результат подбора параметра. Щелкаем на ОК, чтобы сохранить полученные значения ячеек, участвовавших в операции. При этом существует погрешность решения (вместо 0 в правой части уравнения получаем -0,00013).
Пример 2. Найти решение уравнения x2 3x 2 0.
Решение. Уравнение имеет два корня. Решение начинаем с нахождения первого корня.
1.В ячейку А4 вводим заголовок корни, в ячейку В4 – функция.
2.В ячейку А5 вводим ориентировочное значение корня, например, 3.
3.Заносим в ячейку В5 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку А5.
4.Производим подбор параметров. В результате получаем значение первого корня х1=2,000019, значение функции при этом получаем 1,94Е-05 (0,000019).
5.Повторяем расчет для второго корня. Для этого в ячейку А6 вводим значение -3, в ячейку В6 копируем формулу функции. Производим подбор параметров. Значение второго корня х2=0,99960.
Упражнения.
1.Решить уравнение cos(x)=0 в диапазоне х[0;2].
2.Решить уравнение 2x2 3x 1 0
7
3.Решить уравнение x3 3x2 х 0
Тема 3.2 Аппроксимация экспериментальных данных.
Аппроксимацией называется процесс подбора эмпирической формулы (х) для установления из опыта функциональной зависимости y=f(x). Эмпирические формулы служат для аналитического представления опытных данных. Обычно задача аппроксимации разделяется на две части. Сначала устанавливают вид зависимости y=f(x), т.е. решают, является ли она линейной, квадратической, логарифмической и т.п. Обычно определение параметров при известном виде зависимости осуществляется по методу наименьших квадратов. При этом функция (х) считается наилучшим приближением к f(x), если для нее сумма квадратов отклонений теоретических значений (х) найденных по эмпирической формуле, от соответствующих опытных значений минимальна, т.е.
Z n f (xi ) (xi ) 2 min
i 0
ВExcel аппроксимация экспериментальных данных осуществляется путем построения их графика с последующим подбором подходящей аппроксимирующей функции (линии тренда). Возможны следующие варианты функций:
1.Линейная: y=ax+b. Обычно применяется в простейших случаях, когда экспериментальные данные убывают или возрастают с постоянной скоростью.
2.Полиномиальная: y=а0+ a1 x + a2 x2 +… an xn, (п), аi– константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов кривой. Так, например, полином второй степени может описать только один максимум или минимум, полином третьей степени – не более двух экстремумов.
3.Логарифмическая: y a lnx b , где а и b константы, ln – функция натурального логарифма. Функция
применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем стабилизируются.
4.Степенная: y = bxa, где а и b – константы. Аппроксимация степенной функции используется для экспериментальных данных с постоянно увеличивающейся (убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.
5.Экспоненциальная: y = bеaх, где а и b константы, е – основание натурального логарифма. Применятся для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируется. Часто ее использование вытекает из теоретических соображений.
Степень близости аппроксимации экспериментальных данных выбранной функции оценивается коэффициентом детерминации (R2). Чем больше коэффициент детерминации (стремится к единице), тем лучше.
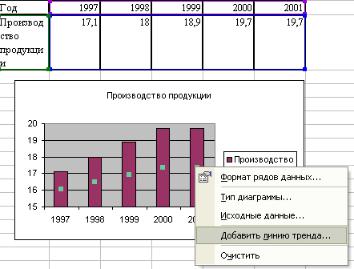
Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать контекстное меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда, на вкладке Тип выбрать вид аппроксимирующей функции, на вкладке Параметры задаются дополнительные параметры, влияющие на отображение аппроксимирующей кривой, в частности можно установить флажки в поля Показывать уравнения на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Можно сделать прогноз о том, как будет вести себя исследуемая функция, для этого надо на вкладке Параметры указать количество периодов (от 0,5) для которых будет сделан прогноз.
Пример: Исследовать характер изменения с течением времени уровня производства некоторой продукции, и подобрать аппроксимирующую функцию, располагая следующими данными.
Год |
1997 |
1998 |
1999 |
|
2000 |
2001 |
|
Производство |
17,1 |
18,0 |
18,9 |
|
19,7 |
19,7 |
|
продукции |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
1. |
Введите данные и постройте гистограмму |
|||
|
|
|
|
зависимости производства продукции от |
|||
|
|
|
|
года. |
|
|
|
|
|
|
2. |
Осуществите аппроксимацию полученной |
|||
|
|
|
|
кривой. Для этого указатель мыши уста- |
|||
|
|
|
|
навливаем на одну из точек гистограммы и |
|||
|
|
|
|
при помощи контекстного меню выбираем |
|||
|
|
|
|
пункт Добавить линию тренда. |
|||
|
|
|
3. |
В окне Линия тренда выберите тип линии |
|||
|
|
|
|
тренда логарифмическая, на вкладке Па- |
|||
|
|
|
|
раметры установить флажки в поля Пока- |
|||
зывать уравнения на диаграмме и Поместить на диаграмму величину достоверности аппроксимации.
8
4.Постройте по исходным данным еще одну гистограмму и произведите те же действия, выбрав тип линии тренда Полиномиальный, степень 2, параметры те же.
5.Сравните полученные уравнения линий тренда и выберите ту, которая лучше аппроксимирует исходные данные, объясните свое решение.
Самостоятельное задание.
1. В средней школе было решено сравнить среднее число книг, прочитанных среднестатистическим восьмиклассником за год, с количеством правонарушений, совершенных подростками в микрорайоне в течение года. Проанализировали данные за 10 лет, получили следующую таблицу:
X |
19 |
25 |
24 |
22 |
18 |
38 |
39 |
30 |
35 |
38 |
Y |
20 |
20 |
15 |
15 |
10 |
4 |
6 |
10 |
10 |
5 |
X – среднее число книг, прочитанных за год , Y – количество правонарушений. Постройте функцию, которая наилучшим образом отображает зависимость количества правонарушений от числа книг, прочитанных за год, и запишите ее уравнение.
2. Количество вложенных в производство средств и полученная в результате прибыль соотносятся следующим образом
Кол-во |
1,6 |
2,0 |
2,5 |
3,0 |
4,0 |
7,0 |
средств (х) |
|
|
|
|
|
|
Прибыль (y) |
8,5 |
9,0 |
11,0 |
13,0 |
22,0 |
70,0 |
Запишите аналитическую зависимость между x и y. Проанализируйте полученный ответ. Какова будет прибыль предприятия, если вложить 10,0 единиц средств?
9
