
Лекции №1
.pdf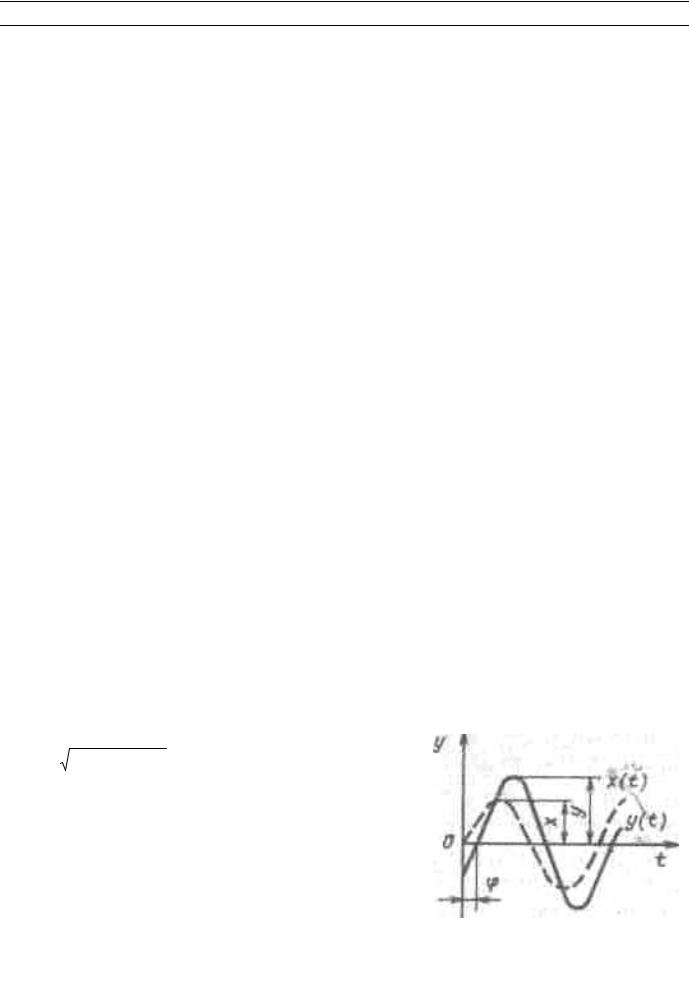
|
A[1] |
|
A/ p |
|
sinω |
t |
|
ω /(p2 |
+ ω |
2 ) |
|
|
|
|
|
|
|
||||||||
|
e±α t |
|
1/(p ± α ) |
|
cosω |
t |
|
p /(p2 |
+ ω |
2 ) |
|
|
|
t |
|
1/ p 2 |
|
e−α t cosω |
t |
(p + α )/[(p + α |
)2 |
+ ω 2 ] |
|
||
|
t 2 |
|
2 / p3 |
|
e−α t sinω |
t |
α /[(p + α |
)2 |
+ α |
2 ] |
|
|
9.6. Частотные характеристики САУ
Частотные характеристики широко используются при анализе и синтезе САУ. Если на вход линейной разомкнутой системы или звена подать гармоническое возмущение (рис. 16), то по истечении некоторого времени, когда затухнут все движения, определяемые переходным процессом, на выходе звена или системы установится также гармоническое изменение выходной величины с той же частотой, которую имеет входная величина, но с иными амплитудой и фазой. Амплитуда и фаза на выходе при прочих равных условиях будут зависеть от частоты
возмущающего воздействия.
Для линейных систем справедлив принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет ограничиться изучением систем только с одним входом.
Рассмотрим несколько понятий, связанных с частотными характеристиками. Периодическое гармоническое возмущение в векторной форме может быть записано
так: x(t) = X e j ω t , где e j ω t = cosω t + j sinω |
t . Последнее выражение представляет со- |
|
бой единичный вектор, |
у которого cosω |
t - вещественная часть, sinω t - мнимая |
часть, X - амплитуда, ω |
t - фазовое состояние процесса. По истечении переходного |
|
процесса на выходе разомкнутой системы установятся вынужденные периодические колебания, определяемые выражением y(t) = Y e j (ω t+ϕ ) = Y e j ω t e jϕ .
Из передаточной функции W ( p) при подстановке p → j ω и находя необходимые производные, получаем передаточную функцию в частотной форме
W ( j ω ) = Y e j (ω t+ϕ ) / X e j ω t = Aω( ) e j ϕ ;
здесь A(ω ) = Y / X зависит от частоты, так же как от частоты зависит и величина ϕ . Так как x(t) и y(t) векторы, то их можно изобразить на комплексной плоскости.
Вектор будет изображен в виде отрезка, длина которого равна амплитуде (рис. 17): W ( j ω ) = U (ω )+ j V (ω ), tgϕ = V (ω )/U (ω ), где U (ω ) - действительная часть, V (ω ) - мнимая часть. Таким образом, передаточная функция в частотной форме есть
векторная |
величина, |
модуль |
которой |
A(ω ) = U 2 (ω )+ V 2 (ω ) , а фаза |
ϕ (ω ) = arctg(V (ω )/U (ω )) |
||
отсчитывается от действительной оси.
При непрерывном изменении частоты происходит изменение модуля и фазы вектора. Конец вектора описывает на комплексной плоскости некоторую кривую, называемую годографом. Годограф - геометрическое место точек конца вектора на комплексной плоскости при изменении частоты от 0 до ∞ . Значения частот откладываются непосредственно на годографе, который, таким образом, является
Рис. 12. Линейная САУ под воздействием гармонического возмущения
21

Рис. 13. Характеристики комплексного |
Рис. 14. Примеры годографоф |
коэффициента усиления |
разомкнутых САУ |
амплитудно-фазочастотной характеристикой. Для определения модуля и фазы передаточной функции на заданной частоте следует соответствующую точку годографа соединить отрезком с началом координат. Его длина соответствует в определенном масштабе модулю, а фаза определяется углом, образованным этой прямой и положительной полуосью действительных величин (рис. 13).
Пример.
Пусть мы имеем ДУ 2 |
|
d 2 y |
+ 0.1 |
dy |
+ y = 2 x ; |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt 2 |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||||
- после преобразования Лапласа имеем 2 p2 Y ( p) + 0,1 p Y ( p) +Y ( p) = 2 X ( p) ; |
|
||||||||||||||||||||||||||||||
- |
передаточная |
|
функция |
|
в |
|
операторной |
|
форме |
имеет |
вид: |
||||||||||||||||||||
W ( p) = |
Y ( p) |
= |
|
|
|
2 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
X ( p) |
2 |
p2 + 0,1 p +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
- |
передаточная |
|
функция |
|
в |
|
|
частотной |
форме |
примет |
вид: |
||||||||||||||||||||
W ( j ω ) = |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
2 |
|
|
|
; |
|
|
|
|
|||
2 ( j ω |
) |
2 |
+ 0,1 ( |
|
jω ) + |
1 |
|
1− 2 ω 2 |
) |
+ j |
0,1ω |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
- найдём модуль частотной передаточной функции: A(ω |
) = |
|
2 |
; |
|||||||||||||||||||||||||||
(1− 2 ω 2 )2 + (0,1ω )2 |
|||||||||||||||||||||||||||||||
- |
|
|
определим |
|
|
|
|
|
|
|
|
|
аргумент |
|
|
|
передаточной |
функции: |
|||||||||||||
ϕ ω( |
) = arctg 0 − arctg |
|
0,1 ω |
|
|
= −arctg |
|
0,1ω |
|
|
; |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
1− 2 ω |
|
|
|
|
|
1− 2ω |
|
|
|
|
|
|
|
|
|||||||||||
- выделим из передаточной функции вещественную и мнимую части:
W ( j ω |
) = |
|
2 |
|
|
|
(1 |
− 2 ω |
2 )− j 0,1ω |
|
2 − 4 ω 2 − j 0, 2ω |
|
||||||
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|||||
(1− 2 ω |
2 )+ j 0,1ω |
(1 |
− 2ω |
2 )− j 0,1ω |
(1− 2 ω 2 )2 + 0, 01ω 2 |
|
||||||||||||
= |
|
2 − 4 ω 2 |
|
+ j |
|
|
|
|
−0, 2ω |
|
; |
|
|
|
|
|
|
|
(1− 2 ω 2 )2 + 0, 01ω 2 |
(1− 2ω |
2 )2 + 0, 01ω 2 |
|
|
|
|
|
|
||||||||||
таким |
образом |
вещественная и |
мнимая части |
частотной передаточной функции |
||||||||||||||
выражаются |
следующими |
уравнениями |
U (ω ) = |
|
2 − 4 ω 2 |
и |
||||||||||||
(1− 2 ω 2 )2 + 0.01 ω 2 |
||||||||||||||||||
V (ω ) = |
|
− 0.2ω |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
(1 − 2 ω 2 )2 |
+ 0.01 ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
(построение характеристик)
22

10.Типовые динамические звенья
10.1. Классификация типовых динамических звеньев
Независимо от физических принципов работы всё многообразие устройств, используемых в САУ может быть сведено к небольшому числу типовых динамических звеньев.
Принадлежность к тому или иному типу динамического звена определяется дифференциальным уравнением движения звена, связывающего входную и выходную величины устройства, изменяющиеся во времени по определенным законам.
По виду оператора введены следующие типовые звенья: усилительное (про-
порциональное, |
безынерционное) |
звено |
Y ( p) = K X ( p) ; |
инерционное |
||
(апериодическое, |
релаксационное) |
звено (T p + 1) Y ( p) = K X ( p) ; |
колебательное |
|||
звено |
(T 2 p2 |
+ T p + 1) Y ( p) = K X ( p) ; интегрирующее звено Y ( p) = [1/(T p)] X ( p) ; |
||||
|
1 |
2 |
|
|
|
|
дифференцирующее звено Y ( p) = T p X ( p) ; запаздывающее звено Y ( p) = e− p τ X ( p) .
10.2. Логарифмические частотные характеристики
При расчетах САУ часто пользуются логарифмической амплитудно-частотной (ЛАЧХ) и логарифмической фазочастотной (ЛФЧХ) характеристиками. В этом случае по оси абсцисс откладывают частоту в логарифмическом масштабе, что позволяет отложить на заданном отрезке значительный диапазон частот. Это наиболее удобная форма представления частотных характеристик для решения задач анализа и синтеза систем. Рассмотрим амплитудно-фазовую
характеристику |
W ( j ω ) = A(ω |
) e j ϕ . Прологарифмируем |
ее: ln(W ( j ω |
)) = ln(A(ω |
)) + j ϕ (ω ) . |
||||||
Перейдём |
к |
десятичным |
логарифмам |
lg(W ( j ω |
)) = lg( Aω( )) + |
|
j |
ϕ (ω ) , |
так |
как |
|
2,3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
ln N = lg N / lg e = lg N / 0,4329 = 2,3 lg N .
Рассмотрим координатную систему для такого представления (рис. 15). По оси абсцисс откладываем величину lgω . Вводим две единицы измерения: декаду, октаву. Декада - длина
отрезка по оси абсцисс, |
соответствующая десятикратному изменению частоты. |
Число декад |
nД = lg(ω В /ω Н ) , где ω В |
- крайняя высокая частота рассматриваемого диапазона; |
ω Н - крайняя |
нижняя частота.
Например, частотный диапазон от ω Н = 1 с−1 до ω В = 10000 с−1 содержит четыре декады, так как lg104 = 4 . Первая декада - от 1 до 10 с−1 , вторая - от 10 до 100 с−1 ; третья - от 100 до 1000
с−1 и т. д. Октава - длина отрезка по оси абсцисс, соответствующая двухкратному изменению частоты. В одной декаде содержится 3,32 октавы. Декадный интервал применяют чаще.
Фазу обычно откладывают по оси ординат в угловых градусах или в радианах. Ординатой амплитудно-частотной характеристики является не величина lg A(ω ) , а пропорциональная ей
величина L(ω ) в децибелах, L(ω ) = 20lg A(ω ) (шкала равномерная). Точка пересечения с осью абсцисс соответствует A(ω ) = 1.
Рис. 15. Координатная система для построения ЛАЧХ и ЛФЧХ
23

Рис. 16. Типовые функции входного сигнала
Использование логарифмического масштаба при построении ЛАЧХ обусловлено не столько значительными изменениями модуля передатчной функции, сколько возможностью осуществления графических методов расчета. При расчетах САУ часто приходится иметь дело с произведением передаточной функции. А так как логарифм произведения равен сумме логарифмов, то при графических расчетах для получения произведения нескольких значений весьма удобно осуществить сложение их логарифмов. Удобство логарифмического масштаба по оси ординат в том, что на одном графике можно представить значения, отличающиеся на несколько порядков.
10.3.Временные характеристики
Временными характеристиками являются переходные и импульсные переходные функции и их графики.
Для определения динамических свойств САУ в качестве входного сигнала применяют следующие типовые функции (рис. 16): единичный скачок; единичный импульс; гармонический сигнал; степенные функция времени.
Переходная функция системы - функция, описывающая изменение выходной величины системы при подаче на её вход единичного ступенчатого воздействия при нулевых начальных условиях. Переходную функцию обычно обозначают h(t) . График переходной функции называют
переходной характеристикой.
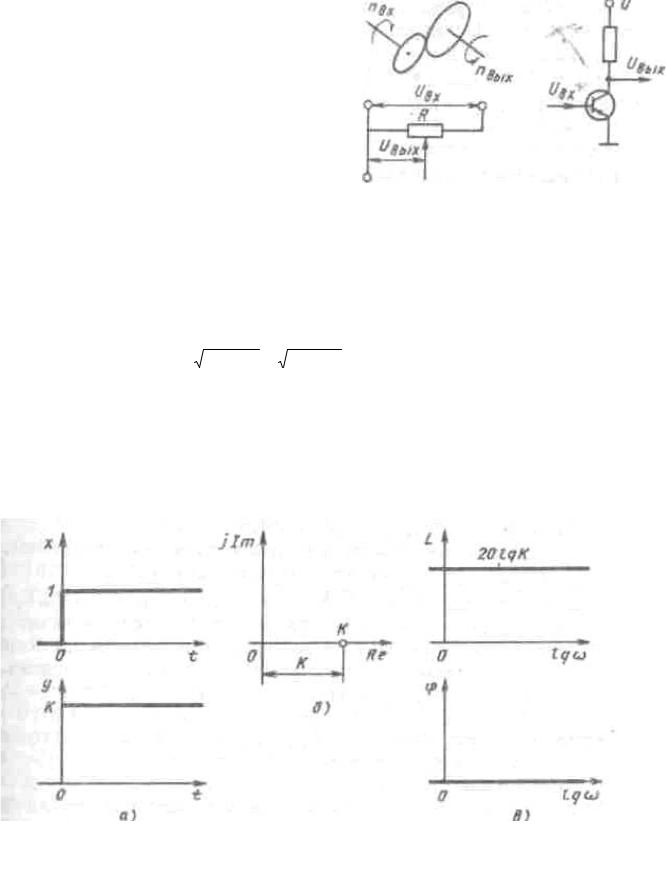
Рис. 17. Условное изображение типовых динамических звеньев: а - пропорциональное; б - инерционное; в - интегрирующее: г - идеальное дифференцирующее; д - реальное дифференцирующее; е - реальное дифференцирующее со статизмом; ж - колебательное; з – запаздывающее
24
Импульсная переходная функция системы - функция, описывающая реакцию системы на единичное импульсное воздействие при нулевых начальных условиях. Её график называют импульсной переходной характеристикой.
Физически единичный импульс - очень узкий импульс единичной площади. Переходную функцию принято вписывать в прямоугольник, изображающий звено (рис. 17).
10.4. Пропорциональное звено
К этим звеньям относятся все устройства, для |
|
|||||
которых в любой момент времени выходная |
|
|||||
величина пропорциональна входной. Входная и |
|
|||||
выходная |
величины |
связаны |
зависимостью |
|
||
y(t) = K x(t) . На рис. 18. показаны примеры техни- |
|
|||||
ческих устройств, описываемых уравнением |
|
|||||
пропорционального звена. |
|
|
|
|
|
|
Алгебраизированное |
|
уравнение |
звена |
|
||
получается, если вместо оригиналов функции |
|
|||||
использовать |
их изображения: |
Y ( p) = K X ( p) . |
Рис. 18. Примеры конструктивного |
|||
Передаточная функция W ( p) = Y ( p) / X ( p) = K . Если |
||||||
предположить, что входной функцией является |
исполнения пропорционального |
|||||
единичный скачок, то переходная функция |
h(t) = 0 |
звена |
||||
при t < 0 и |
h(t) = K при |
t ≥ |
0 (рис. 19,а), |
так как |
|
|
x(t) = 0 при t < 0 и x(t) = 1 при t ≥ |
0 , т. е. переходная функция повторяет входную, но ордината |
|||||
будет в K раз больше. Передаточная функция содержит только действительную часть, равную K , |
||||||
а мнимая равна нулю, |
аргумент |
вектора |
ϕ = 0 , |
так как ϕ (ω ) = arctg(V /U ) = 0 . Модуль |
||
передаточной функции A(ω |
) = |
U 2 + V 2 = K 2 + 02 = K . |
||||
Годограф звена (рис. 19,б) - точка на комплексной плоскости, расположенная на оси действительных величин на расстоянии K . Интерпретация годографа: с изменением частоты от
нуля до бесконечности модуль вектора передаточной функции остается равным K ; звено не
вносит фазовых сдвигов, так как при всех значениях частоты фазовый угол остается равным нулю (вектор совпадает с положительной полуосью действительных величин).
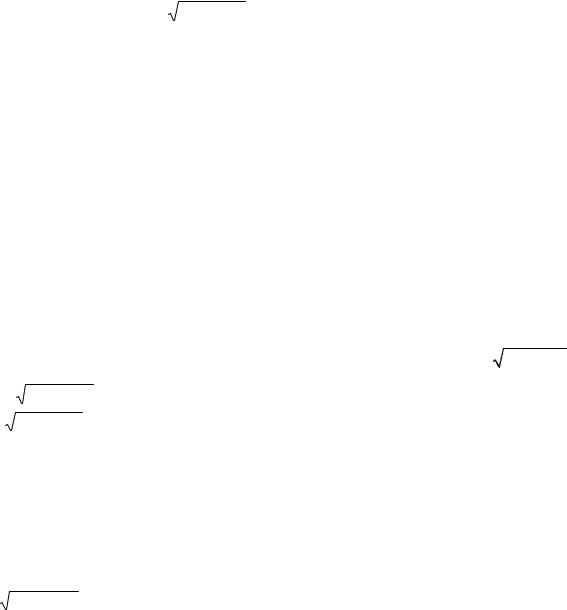
Аналитическое выражение для ЛАЧХ: L(ω ) = 20 lg A(ω ) = 20lg K (рис. 19,в). Поскольку ϕ = 0 для всех частот, то фазовая характеристика совпадает с осью частот.
Рис. 19. Характеристики пропорционального звена: а - переходная; б - амплитудно-фазовая; в - ЛАЧХ и ЛФЧХ
25
10.5. Инерционное звено
Звено называют инерционным, если связь между выходом и входом звена определяется
дифференциальным уравнением вида T dy / dt + y(t) = K x(t) . |
|
|
|
||||
Уравнение в |
операторной форме |
T p Y ( p) + Y ( p) = K X ( p) . Передаточная |
функция |
||||
W ( p) = Y ( p) / X ( p) = K /(1 + p T ) . Переходим к чатотной форме W ( j ω ) = K /(1+ j ω T ) . |
|||||||
Построение годографа. В выражении |
W ( j ω ) умножим |
числитель и |
знаменатель на |
||||
комплексно |
сопряженный |
знаменатель |
(1 − j ω T ) , |
|
тогда |
||
W ( j ω ) = K /(1+ ω 2 T 2 ) − K ω |
T /(1+ ω 2 T 2 ) , |
где |
U (ω ) = K /(1+ ω 2 T 2 ) , |
||||
V (ω ) = −K ω T /(1 + ω 2 T 2 ) . |
|
2 T 2 , ϕ ω( ) = arctg (Vω( |
)/Uω ( )) = −arctgω ( |
|
|||
Модуль и аргумент - A(ω |
) = K / 1 + ω |
T ) . При |
|||||
ω = 0 U (ω ) = K , V (ω ) = −0 . При ω = 1/ T |
U (ω |
) = K / 2 , V (ω ) = −K / 2 . При ω → ∞ |
U (ω |
) = 0 . Для |
|||
раскрытия неопределенности V (ω ) при ω |
→ ∞ |
можно числитель и знаменатель выражения для |
|||||
V (ω ) разделить на ω |
T : V (ω ) = K /(1/ ω T )+ ω |
T = −0 . |
|
|
|
||
Нет необходимости задавать большое число значения ω для более точного построения годографа. Можно найти уравнения кривой годографа в канонической форме. Для этого следует
рассмотреть выражение U 2 (ω |
)+ V 2 (ω |
).Так как U (ω ) = K /(1+ ω |
2 T 2 ) , V (ω |
) = K ω T /(1 + ω |
2 T 2 ) , |
||||||||||
то U 2 (ω )+ V 2 (ω |
) = K 2 /(1+ ω |
2 T 2 )2 |
+ K 2 ω 2 |
T 2 / (1+ω 2 T 2 )2 |
= K Uω ( |
). |
Прибавим к |
обеим |
|||||||
частям равенства |
по K |
2 |
/ 4 |
и получим U |
2 |
(ω ) − K U ω( ) + K |
2 |
|
2 |
) = K |
2 |
/ 4 . Первые три |
|||
|
|
|
/ 4 +V ω ( |
|
|||||||||||
члена левой части представляют собой квадрат разности двух членов. Перепишем уравнение как:
(U (ω )− K / 2)2 + (V (ω |
)− 0)2 = (K / 2)2 . Это уравнение окружности, |
радиус которой равен |
K / 2 , а |
||||||||
центр ее расположен в точке |
A с координатами |
(K / 2, j 0), т. е. годограф описывает кривую, |
|||||||||
представляющую собой полуокружность (рис. 20,а). Ось мнимых величин V (ω ) является |
|||||||||||
касательной к |
этой |
окружности. Фазовый угол меняется от нуля |
до −π / 2 . |
Модуль имеет |
|||||||
наибольшее значение, равное K при ω |
= 0 и равное 0 при ω |
= ∞ . |
|
) = 20 lg (K / 1ω+ |
2 T 2 )= |
||||||
Аналитическое |
выражение |
для ЛАЧХ: |
L (ω |
) = 20 lg Aω( |
|||||||
= 20 lg K − 20 lg |
1 + ω |
2 T 2 . |
ЛАЧХ |
состоит |
из |
двух |
слагаемых |
L (ω ) = 20 lg K и |
|||
L2 (ω ) = −20lg |
|
|
|
|
|
|
|
|
|
1 |
|
1+ ω 2 T 2 . Первое слагаемое не зависит от частоты, |
и поэтому графически его |
||||||||||
изображают прямой (рис. 20,б), параллельной оси абсцисс с ординатой 20lg K . Для графического
построения второго слагаемого прибегают к приему, сущность которого сводится к замене |
|||||||
некоторой плавной кривой |
L2 (ω ) = f (lgω ) двумя |
сопрягаемыми прямыми, одна из которых |
|||||
определяет изменение L(ω ), |
в области низких частот, |
другая - |
в области высоких частот. Эти |
||||
прямые являются асимптотами кривой L2 (ω ) = f (lgω |
), |
а полученную характеристику называют |
|||||
асимптотической ЛАЧХ. |
частот, где ω T < 1 , а |
|
2 T 2 << 1, |
L2 (ω ) = −20lg1, так как при |
|||
В |
области низких |
ω |
|||||
ω 2 T 2 |
<< 1, 1+ ω 2 T 2 |
= 1, т. е. величиной ω 2 T 2 |
пренебрегают по сравнению с единицей. Так |
||||
как lg1 = 0 , то в области низких частот L2 (ω ) ≈ −0 . Знак «-» имеет определенный смысл: строго говоря, характеристика проходит не на нулевом уровне, а в области отрицательных значений. В
области частот, где |
ω T > 1 |
, а ω 2 T 2 >> 1 и L (ω |
) ≈ − 20 lgω( |
T )= − 20ωlg − 20 lgT , получаем |
|||
|
|
|
|
2 |
|
|
Величина L2 (ω ) = −0 , т. е. |
уравнение |
прямой, |
так |
как |
аргументом является |
величина |
lgω . |
|
L (ω ) = L1 ω( |
) , если lgω |
T = 0 , а ω T = 1. |
|
|
|
||
Таким образом, прямые L2 (ω ) и L1 (ω ) сопрягаются там, где ω C |
= 1/T . Эту частоту принято |
||||||
называть частотой сопряжения. Поскольку прямая |
L2 (ω ) определяется точкой с координатами |
||||||
|
|
|
|
|
|
|
26 |
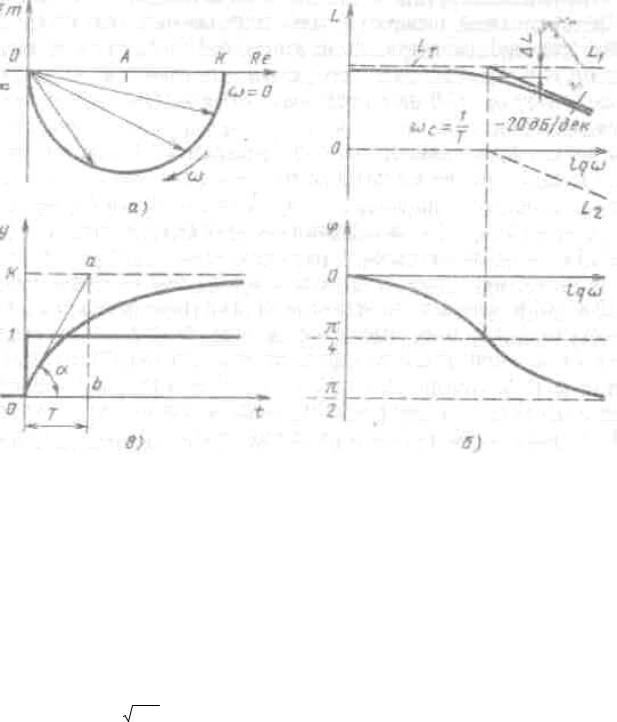
Рис. 20. Характеристики инерционного звена: а - амплитудно-фазовая; б - ЛАЧХ и ЛФЧХ; в - переходная
L2 (ω ) = 0 и ω C = 1/T , то для её построения достаточно определить угловой коэффициент прямой.
Определим для этого изменение ординаты, приходящееся на одну декаду, т. е. рассмотрим |
||||||||||||||||||
значение |
L2 (ω |
) |
|
на |
частотах |
ω |
i , |
и |
10 ω |
i : |
L2′ (ω ) = −20 lgω i T , |
|||||||
L′′(ω ) = −20 lg(10ω |
i |
T ) = −20lg10 − 20lg(ω |
i |
T ) = −20lg10 |
+ L′ . |
Отсюда |
L′′(ω |
)− L′ (ω ) = −20 дБ. |
||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2 |
|
|
||
Следовательно, наклон составляет 20 дБ/дек. |
|
|
|
|
|
|
|
|
|
|||||||||
|
Для определения наибольшей ошибки, получаемой при замене очной ЛАЧХ |
|||||||||||||||||
асимптотической, |
определим ∆ L |
при частоте |
ω |
C . В |
этом |
случае |
ордината |
асимптотической |
||||||||||
ЛАЧХ La (ω ) = 20 lg K , а ординату для |
точной |
ЛАЧХ определяют |
из |
условия, что |
ω |
T = 1, |
||||||||||||
LT (ω ) = 20 lg K − 20 lg |
1 +1 = 20lg K − 3. |
Поправка к асимптотической ЛАЧХ ∆ L = La − LT |
= 3 дБ. |
|||||||||||||||
В |
ряде |
случаев |
(ω |
этой |
поправкой |
пренебрегают. |
Аналитическое |
выражение |
|
ЛФЧХ: |
||||||||
ϕ (ω |
) = arctgV (ω )/U |
) = arctg(− ω |
T ) = −arctgω |
T . При ω = 0 ϕ = 0 , при ω |
= 1/ T , |
т. е. при |
||||||||||||
частоте сопряжения ω |
T = 1 ϕ = −π / 4 . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В области низких частот инерционное звено не вносит заметного сдвига фаз, но в области |
|||||||||||||||||
высоких частот это звено вносит отставание по фазе, |
стремящееся к − π / 2 рад. Если входная |
|||||||||||||||||
координата - единичная функция, |
изображением которой является X ( p) = 1/ p , то изображение |
|||||||||||||||||
выходной |
координаты, |
являющейся |
в этом |
случае |
переходной |
функцией, |
является |
|||||||||||
Y ( p) = X ( p) W ( p) = (1/ p) (K /(1 + p T )) = K / ( p + p2 T ) , её оигинал |
y(t) = K |
(1− e−t / T |
). На рис. |
|||||||||||||||
20,в представлено графическое изображение этой функции. Кривая - экспонента, асимптотически приближающаяся к прямой с ординатой, равной K .
Когда необходимо определить постоянную времени T , можно, сняв кривую переходного процесса, например, осциллографированием, по ней определить значение T . Оказывается, что касательная, проведенная к снятой кривой из начала координат, отсекает на прямой K отрезок,
27

равный T . В самом деле, из треугольника Oab следует, что Ob = ab / tgα , но так как ab = K , то
Ob = K / tgα |
. Первая производная от |
функции определяет тангенс угла наклона |
касательной, |
поэтому tgα |
= dy / dt = K (1/ p) e−t / T |
и при t = 0 tgα = K / T . Отсюда Ob = K |
/ tgα = T , но |
Ob = K a , следовательно, K a = T .
Чем больше постоянная времени T , тем медленнее протекает процесс, тем более полога экспонента. Если T является малой величиной и, скажем, T стремится к 0, то экспонента уподобляется скачкообразно меняющейся функции, что присуще пропорциональному звену. Более того, если T стремится к 0, то в выражении для передаточной функции инерционного звена
W ( p) = K / (1+ p T ) знаменатель стремится к единице, а передаточная функция в пределе ничем не отличается от передаточной функции пропорционального звена W ( p) = K .
Примерами конструктивного выполнения инерционного звена являются генератор постоянного тока с независимым возбуждением (входная величина - напряжение возбуждения; выходная - напряжение якоря генератора); термопара (входная величина - температура окружающей среды, выходная - термоЭДС), электрический двигатель постоянного тока (вход - сила тока якоря, вых - частота вращения).
10.6. Интегрирующее звено
Для интегрирующего |
звена |
связь между входной |
и |
выходной |
величиной |
выражается |
|
|
∞ |
|
|
|
|
|
|
соотношением |
y(t) = K ∫ x(t)dt . |
В операторной форме |
связь между |
входной |
и выходной |
||
|
0 |
|
Y ( p) = K (1/ p) X ( p) . |
|
|
|
|
координатами |
записывается |
так: |
В |
операторной форме |
символ ∫ |
||
заменяется множителем 1/ p ; в этом нетрудно убедиться, если продифференцировать выражение
|
|
∞ |
|
|
|
|
|
|
|
y(t) = K ∫ x(t)dt , |
dy / dt = K x(t) . |
В |
операторной |
форме |
p Y ( p) = K X ( p) |
и |
|||
|
|
0 |
|
|
|
|
|
|
|
Y ( p) = K (1/ p) X ( p) . Отсюда W ( p) = Y ( p) / X ( p) = K / p . Если K = 1/ T , то W ( p) = 1/ ( p T ) . |
|
||||||||
|
|
При некоторых условиях инерционное звено уподобляется интегрирующему. В самом деле |
|||||||
WИ ( p) = K1 /(1 + p T1 ) |
, a WИТ ( p) =1/ ( p T ) . |
Если p T1 |
>> 1, то |
WИ ( p) = K1 / ( p T1 ) , а |
при |
||||
K |
1 |
/T = T ′ |
W ( p) = 1/ |
( p T′) . |
|
|
|
|
|
|
1 |
И |
|
|
|
|
|
|
|
Таким образом, инерционное звено с большой постоянной времени на сравнительно высоких частотах подобно интегрирующему звену. Передаточная функция интегрирующего звена в частотной форме
W ( j ω |
) = K / ( jω ) |
|
или |
W ( j ω |
) = − j K ω/ . |
|
При |
изменении ω от 0 |
до |
∞ |
|
K( j ω |
) меняется от |
− ∞ |
до |
0, но остаётся всегда мнимой
величиной. |
|
|
|
Годограф |
представляет |
собой прямую, |
совпадающую |
|
с |
осью |
отрицательных |
мнимых величин (рис. 20,а).
Модуль |
передаточной |
|
функции |
A(ω ) = K /ω |
и |
аналитическое выражение для ЛАЧХ
L (ω ) = 20lg (K ω/ ) = −20lgω ( T )
, где T = 1/ K . ЛАЧХ (рис. 21,б) представляет собой
Рис. 21. Характеристики интегрирующего звена: а – амплитудно-фазовая; б – ЛАЧХ и ЛФЧХ; в -
переходная
28

прямую, пересекающуюся с осью |
|
||||||
lgω |
на |
частоте |
ω |
= 1/T = K . |
|
||
Наклон прямой равен |
− 20 дБ/дек. |
|
|||||
Так как выражение для W ( j ω ) |
не |
|
|||||
содержит |
действительной |
части |
|
||||
(U (ω ) = 0), то фазовый угол на всех |
|
||||||
частотах |
остается |
неизменным |
и |
|
|||
равным ϕ |
= arctg(− ∞ ) = −π |
/ 2 . |
|
|
|||
|
Изображение |
|
переходной |
|
|||
функции: |
|
|
|
|
|
Рис. 22. Примеры конструктивного исполнения |
|
Y ( p) = (K / p) 1/ p = K / p2 , |
|
а |
интегрирующего звена |
||||
оригинал |
y(t) = K t . |
Переходная |
|
||||
характеристика - прямая, проходящая через начало координат с угловым коэффициентом K (рис. 21,в).
Примерами интегрирующего звена являются гидравлический демпфер (рис. 22,а), поршень под действием силы P перемещается, и жидкость через отверстие в поршне перетекает из правой
части в левую. Тогда v = dx / dt = P a где a - коэффициент сопротивления, x = (1/ a) ∞∫ Pdt . В
0
редукторе (рис. 22,б) входной величиной является частота вращения nВХ входного вала, выходной - угол поворота α ВЫХ выходного вала. В электрическом двигателе можно пренебречь
электромеханической постоянной времени и механической постоянной ротора; входом считается напряжение питания а выходом - угол поворота вала ротора.
10.7. Реальное дифференцирующее звено
Если функционирование какого-либо устройства независимо от принципа действия описывается дифференциальным уравнением вида T dy / dt + y(t) = T dx / dt , то с точки зрения теории автоматического управления устройство относится к динамическому звену типа реального
дифференцирующего, |
|
описываемого |
в |
операторной |
форме |
уравнением |
Y ( p) + p T Y ( p) = p T X ( p) , передаточная функция W ( p) = p T / |
(1+ p T ). |
|
||||
Так |
как |
изображение |
переходной |
функции |
||
Y ( p) = W ( p) X ( p) = p T /(1+ p T ) 1/ p = T /(1+ p T ), то ее оригинал y(t) = e−t /T |
(рис. 23,а). |
|||||
Когда аналитическое определение величины T затруднительно, значение постоянной времени можно найти, если провести касательную к экспоненте, полученной путем осциллографирования при t = 0 . Отрезок, отсекаемый касательной от начала координат на оси абсцисс, в соответствующем масштабе определяет постоянную времени.
Построение |
годографа. |
|
Передаточная функция в частотной |
|
|
форме |
|
|
W ( j ω ) = j ω T /(1+ j ω T ). |
|
|
Умножим числитель и знаменатель |
Рис. 23. Характеристики реального |
|
на комплексно-сопряженное число |
||
(1− j ω T ). |
Выражение |
дифференцирующего звена: ф – переходная; б – |
принимает |
вид |
амплитудно-фазовая; в – ЛАЧХ и ЛФЧХ |
29
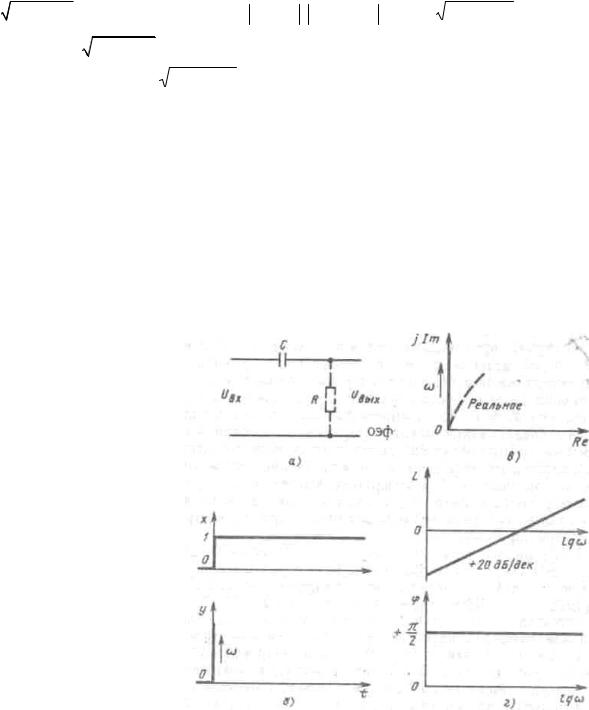
W ( j ω ) = ω 2 |
T 2 /(1+ ω 2 T 2 )+ j ω T /(1+ ω 2 T 2 ), |
где |
U (ω ) = ω 2 T 2 /(1+ ω 2 T 2 ), |
|
V (ω ) = ω T /(1 + ω 2 T 2 ). |
|
|
||
Годограф звена располагается в первом квадранте комплексной плоскости, так как при всех |
||||
значениях ω |
U (ω |
) > 0 и V (ω ) > 0 , и представляет собой полуокружность радиусом r = 1/ 2 с |
||
центром в точке |
A с координатами (1/ 2, j0) (рис. 23,б). Из анализа годографа видно, что при |
|||
изменении частоты от нуля до бесконечности модуль меняется от нуля до 1, а фаза пробегает все значения от + π / 2 до 0 (при ω = 1/ T фазовый угол равен 45°).
|
Построение |
ЛАЧХ. |
Аналитическое выражение для ЛАЧХ: |
L(ω ) = 20 lg A(ω ) = |
|||||||||||||
= 20lg (ω T / |
1+ω |
2 T 2 ). |
Модуль |
|
A(ω ) = j ω T /1+ j ω |
T = ω T / |
1+ ω |
2 T 2 . |
Тогда |
||||||||
L (ω |
) = 20lgω( |
T ) − 20 lg |
1ω+ |
2 T 2 . |
Это |
выражение можно представить |
так: |
L = L + L |
2 |
, где |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
L (ω |
) = 20lgω( |
T ) , а L |
2 |
(ω ) = −20lg 1+ ω 2 T 2 . |
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Слагаемое L1 (ω ) графически можно изобразить в виде |
бесконечной прямой, идущей |
с |
||||||||||||||
наклоном +20 дБ/дек. и пересекающей ось абсцисс в точке ω |
= 1/ T . Второе слагаемое L2 (ω ) |
в |
|||||||||||||||
области низких частот (ω |
T < 1) |
графически представляет |
собой прямую, |
практически |
|||||||||||||
совпадающую с осью абсцисс, а в области высоких частот при (ω |
T > 1) - прямую с наклоном - 20 |
||||||||||||||||
дБ/дек., прямые сопрягаются в точке, где (ω T ) = 1. В результате графического сложения L1 (ω ) и |
|||||||||||||||||
L2 (ω ) результирующая характеристика |
L(ω ) в области низких частот - |
прямая |
с наклоном |
||||||||||||||
+20дБ/дек., а в области высоких частот, где ω > 1/ T , результирующая характеристика совпадает с |
|||||||||||||||||
осью абсцисс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Построение ЛФЧХ. ϕ ω( |
) = arctgω( |
T / 0) − arctgω ( T ). |
|
|
|
|
|
|
|
|
||||||
|
Результирующая фазовая характеристика определяется суммой двух характеристик, одна из |
||||||||||||||||
которых не зависит от частоты и |
|
|
|
|
|
|
|
|
|
||||||||
равна |
π / 2 , |
а |
другая |
- |
частотно |
|
|
|
|
|
|
|
|
|
|||
зависима. В области низких частот |
|
|
|
|
|
|
|
|
|
||||||||
звено вносит опережение, близкое к |
|
|
|
|
|
|
|
|
|
||||||||
π / 2 , |
а в области высоких частот |
|
|
|
|
|
|
|
|
|
|||||||
фазовый угол стремится к нулю.
10.8. Идеальное дифференцирующее звено
Связь |
между |
входной |
и |
|
выходной координатой |
имеет |
вид |
||
y(t) = T dx / dt |
т. |
е. |
выходная |
|
координата в некотором масштабе, определяемом величиной T , равна первой производной от входной координаты. В идеально дифференцирующем звене выходная величина пропорциональна скорости изменения входной величины. Такое звено представлено на рис. 24,а, где выходное сопротивление близко к нулю.
При изменении входной величины переходный процесс в таком звене теоретически происходит мгновенно. При подаче на вход
Рис. 24. Характеристики идеального дифференцирующего звена: а – электрическая модель звена; б - переходная; в - амплитуднофазовая; г - ЛАЧХ 1 ЛФЧХ
30
