4.1.1. Математическое ожидание

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Аксенчик А. В. - Теория вероятностей и мат статистика. Уч. мет. пос.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 249 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

ГЛАВА 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

4.1. Числовые характеристики одномерной случайной величины

личин используют некоторые величины, которые называются числовымиРха-

При решении многих практических задач нет необходимости указывать

полностью закон распределения случайной величины, а можно указать наибо-

лее характерные его черты. Поэтому для общей характеристики случайных ве-

рактеристиками. Они позволяют в сжатой форме выразить наиболее суще-

ственные особенности того или иного распределения. Важнейшими из них яв-
			И
ляются: математическое ожидание, дисперсия, среднее квадратическое откло-
нение.		У
		У
	Г
	4.1.1. Математическое ожидание
	Б
Одной из важнейших характеристик случ йной величины является мате-

чайной величины – это не точное опр д л ние, смысл математического ожи-

матическое ожидание. Математичес гкоое ожид ние – это среднее значение слу-

дания. Математическое ожидание л

вычисляется и

обладает полезным

свойством: среднее арифметическое одинаково распределенной случайной ве-

личины близко к математическомуеожиданию.

Пусть 1

дискретное

пространственное элементарных

, 2,..., N –

этих

событие. Рассмотрим с бытие

состоящее в том, что случайная величина Х

принимает значен е xk , . е. k

{X xk}. Пусть события k – равновероятны,

тогда вероятности

событий: P

1,N

Тогда среднеелзначение случайной величины можно определить так:

б1

x1 ... xN / N

x1 ...

учтем, что

P( k )

xk P( k ) .

k 1

В общем случае вероятности P k pk

могут и не быть одинаковы.

Тогда среднее значение вычисляется по формуле

p1x1 p2x2 ... pN xN pkxk .

k 1

Будем обозначать математическое ожидание случайной величины X как M[X] или mx .

Математическим ожиданием дискретной случайной величины Х на-

зывается сумма произведений всех возможных значений случайной величины на их вероятности:

M X xk pk .

(4.1)

k 1

Рассмотрим непрерывную случайную величину X, все возможные значе-

ния которой

принадлежат интервалу [a, b]. Пусть f(x) – плотность распределе-

ния. Разобьем интервал [a, b]

на n отрезков x1, x2... xn .

Вероятность попада-

ния случайной

величины

на элементарный

участок

xk равна

pk f xk xk ,

). Тогда по аналогии с определением математического

1,n

ожидания для дискретной случайной величины запишем

xk pk xk f xk xk .

0 , получим определенныйИинтеграл:

k 1

Перейдем к пределу при

x dx.

lim

xk 0

k 1

величины Х,

Математическим ожиданием непрерывной случайной

возможные значения которой принадлеж т отрезку [a,b] называется опреде-

ленный интеграл:

кa

M X xf x dx.

(4.2)

всей числовой оси,

Если плотность распред л ния f(x) определена на

тогда:

M X xf x dx.

(4.3)

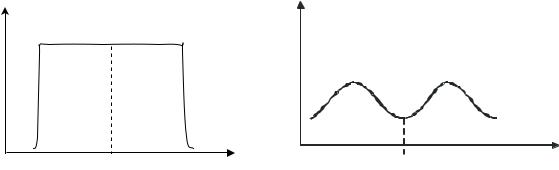
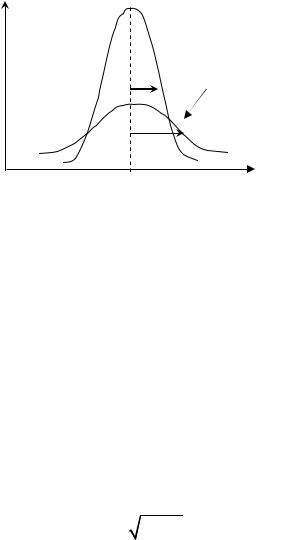
Физическ й смысломатематического ожидания. Математическое ожида-

ние – это абсцисса центра тяжести стержня, имеющего массу, равную единице, с плотностью f(x). Равномерное распределение плотность f(x) по длине стержня показано на рис. 4.1. Неравномерное распределение плотности f(x) показано на

рис. 4.2.	б
	б	f (x)
f(x)		f (x)
f(x)
и
Б

mx	X	x
	X	mx
		mx
Рис. 4.1		Рис. 4.2

4.1.2. Общее определение математического ожидания

При решении практических задач часто используются функции случайных величин, например: Y X2 , Y sin(X) и т. д. Очевидно, что если X случайная величина, то и Y тоже случайная величина, но с определенной функцио-

нальной	зависимостью от	Х. Пусть задана функциональная зависимость
Y X	. Требуется найти	математическое ожидание случайной величины Y,

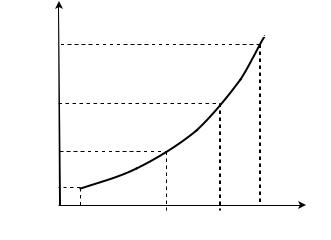
зная плотность распределения случайной величины X. Для простоты предположим, что X – монотонная непрерывная и обратная функция X 1 Y –

однозначна (рис. 4.3).

(b)

y (x)

yi 1

(a)

i 1

кi

еРис. 4.3

Рассмотрим событие с с

ящее в том, что случайная величина Х попадет

в промежуток [ x

x ): x

тX x , в этом случае выполнится событие, со-

i 1

стоящее в том, что

учайная величина Y попадет в промежуток [ yi 1, yi ):

yi 1 Y yi . Эти события

равносильны,

т.

е. событие xi 1 X xi влечет

событие yi 1 Y yi			и наоборот. Это означает, что между точками промежут-
ка [xi 1,xi)		л
	[yi 1,yi) существует взаимно однозначное соответствие.
	б
Раз события равносильны, то вероятности этих событий одинаковы:
и			P xi 1 X xi P yi 1 Y yi .	(4.4)
Обозначим плотность распределения случайной величины Y как				f (y) и
Б

положим a и b , тогда, используя (4.2) математическое ожидание случайной величины Y, определим так:

M Y yf y dy= ранее мы показали, что этот интеграл является пре-

делом следующей суммы

= lim

f y

k 1

учтем, что P(y

Y y

) f (y) y

i 1

lim

k 1

P y

k 1

Y y

с учетом (4.4) перейдем к переменным Х

lim

P x

) x

x f

(x)dx.

xk 0

k 1

Таким образом, общее определение математического ожиданияРдля не-

прерывной случайной величины запишется так:

M (X) (x) f (x)dx.

(4.5)

Если случайная величина Х определена на всей числовой оси: a

интеграл

существует, то

b и, соответственно, несобственный

M x

(4.6)

Для дискретной случайной в личины Х общее определение математиче-

ского ожидания запишется так:

M x

p .

(4.7)

k 1

плучить формулы общего определения математиче-

Аналогично м

для

двумернойжно

случайной величины (X, Y), если задана функ-

ского ожидания

мость

Z (X,Y)

и известен закон распределения двумер-

циональная зав с

ной случайной ве ичины (X, Y).

Для непрерывной случайной величины

и
и		m	n
Б		m	n
	M (X,Y)		(x,y) f (x,y)dxdy.

Для дискретной случайной величины
	M X,Y			(x ,y	)p .
				i j	ij

j 1 i 1

4.1.3.Свойства математического ожидания

1.Если С не случайная величина (т. е. постоянная), то математическое ожидание от С равно самой величине С:

M C C.

Доказательство:

Неслучайную величину С можно рассматривать как дискретную случай-

ную величину с единственным значением С, которому соответствует вероят-

ность Р = 1. Тогда по определению математического ожидания (4.1)

M C 1*C C .

2. Свойство аддитивности. Математическое ожидание суммы случайных

величин равно сумме математических ожиданий:

M X

Y M X M Y .

Доказательство:

Из определения математического ожидания имеем

M X Y

x y f

x,y dxdy

xf (x,y)dxdy

yf (x,y)dxdy

x f x,y dy dx y f x,y dx dy

с учетом свойства 4 двум рной плотности,

xf1

формулы

(3.5), получим

y dy

M Y

Аналогично доказывается

M X Y M X M Y .

множитель, то его можно выносить за знак мате-

3. Если

С – постоянныйи

матического ожидания:

M CX CM X .

Доказательство:

Воспользуемсяи

общим

определением

математического ожидания для

Y x (4.6).

Пусть Y CX , тогда M CX	Cxf x dx C xf x dx CM X .

4.Мультипликативное свойство. Для независимых случайных величин X

иY математическое ожидание произведения этих величин равно произведению их математических ожиданий:

M XY M X M Y .

Доказательство:

M X Y

xyf x,y dxdy

с учетом независимости случайных величин

xf1 x dx

формула (3.13): f x,y f x f

y , получим

y dy M

M Y .

5. Величина

X M X

называется центрированной случайной величиной,

обозначим ее X . Тогда справедливо следующее соотношение

M X M X 0.

Доказательство:

M X M X M

M M X

M X M X 0.

Кроме математического ожидания, которое является основной характери-

стикой положения случайных величин на числовой оси, на практике применяют

и другие числовые характеристикик, описывающие центр распределения случайной величины, в частности моду, м диану.

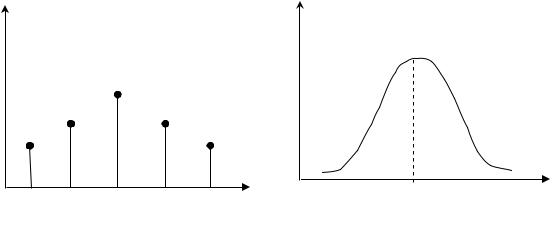
Модой дискретной случайной в личины X называют ее наиболее вероят-

ное значение (рис. 4.4). Модой н пр рывной случайной величины называется
						е
такое ее значение xmod , при ко ором плотность распределения имеет максимум
(рис. 4.5).					т
Pi					т		f(x)
Pi				о			f(x)
				о
			и
		л
	б
и
Б						x			x
								xmod
			xmod
			xmod


				Рис. 4.4				Рис. 4.5

f (x)

xm1	xm2	x	a		x
				b

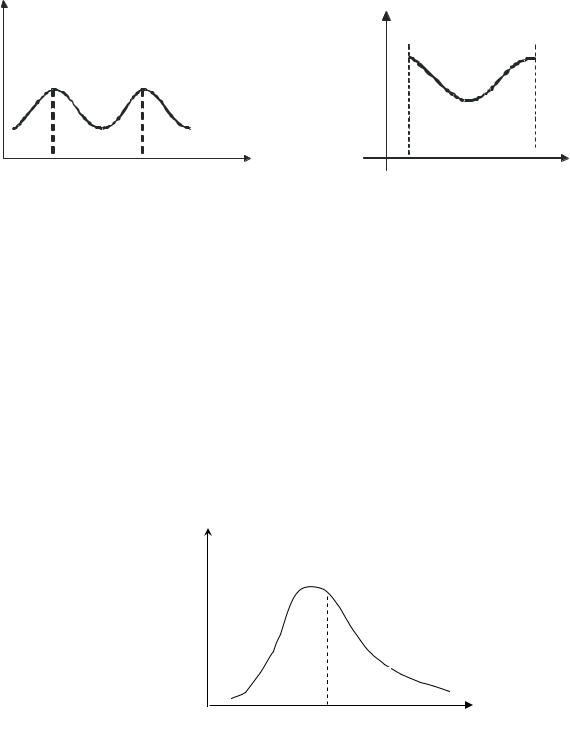
	Рис. 4.6			Рис. 4.7

Распределения случайных величин бывают одномодальные (рис. 4.5),

двумодальные (рис. 4.6), полимодальные и антимодальные – моды не имеют
(рис. 4.7).				У	Р
Для определения
		моды необходимо продифференцировать плотность
распределения –	f ' x ,		Г
		приравнять к нулю производную: f ' Иx 0, и решить
это уравнение относительно x.			Б
Медианой
	xmed произвольной случайной величины X называют такое ее

значение, относительно которого равновероятно получение большего или

чины – это абсцисса точки, в которой

площадьфигуры, ограниченной сверху

меньшего значения случайной величины:

P(X xmed ) P(X xmed ) 0,5.

С геометрической точки зрения

меди на непрерывной случайной вели-

0,5 (рис. 4.8).

кривой распределения, делится пополамкp p

f(x)

xmed

Рис. 4.8

Если распределение одномодальное и симметрическое, то все три характеристики положения случайной величины: математическое ожидание, мода и медиана – совпадают.

Квантилем порядка р называется значение случайной величины xp , оп-

ределяемое из уравнения
F xp P.	(4.8)
64

Очевидно, что квантиль порядка 0,5 – это медиана, которая определяется из уравнения F xmed 0,5.

4.1.4. Дисперсия, среднее квадратическое отклонение

При проведении вероятностных экспериментов можно заметить, что значения случайных величин всегда колеблются около среднего значения. Это явление называется рассеиванием случайной величины около ее среднего значения.

Числовые характеристики, описывающие рассеивание случайной величины,
		И
показывают, насколько тесно сгруппированы возможные значения случайной
величины около ее среднего значения – математического ожиданияР.
Основными из них являются дисперсия и среднее квадратическое откло-
нение.	Г

Для определения этих характеристик используется разность между слу-
0	Б

чайной величиной X и ее математическим ожиданием. РанееУв свойстве 5 мате-

матического ожидания мы дали определение, в котором центрированная слу-

чайная величина обозначается	0		а	X M X . В свойстве 5
	X и определяется как
		к
мы показали, что M[X] 0 , т. е. матем тическое ожидание центрированной
	е

случайной величины никак не хара теризует ее рассеивание, а указывает лишь на то, что значения отклонения – числа разного знака. Поэтому в качестве меры рассеивания случайной величины б рут математическое ожидание квадрата

центрированной случайной величины.
Дисперсией	величины X называется математическое ожида-

ние квадрата отклонения случайной величины от ее математического ожида-

ния и обозначается

случайной

X M[X]

(4.9)

D X M

Испо ьзуя общее определение математического ожидания (4.6), легко

записать дисперсиюлдля непрерывной случайной величины, если обозначить

(x) (X m

)2 :

D X x mx f

x dx.

(4.10)

Аналогично, применив формулу (4.7), дисперсия для дискретной случай-

ной величины

D X xi mx 2

pi .

(4.11)

i 1

Подчеркнем еще раз смысл дисперсии: дисперсия – мера рассеивания (или отклонения) случайной величины относительно ее математического ожидания.

f(x)	D1
		D2
				Р
	mx		x


	Рис. 4.9
	Рис. 4.9
На рис. 4.9 показаны два варианта распределения для двухИразных слу-
		Г

чайных величин. Видим, что у более плоской кривой отклонение от среднего

значения mx (можно взять по среднему уровню кривой) большеУ, чем у остроко-

нечной кривой. Значит, дисперсия D2

будет больше дисперсии D1.

Использование дисперсии хотя и удобно для характеристики рассеивания

случайной величины X, но лишено наглядности, т. к. имеет размерность квад-

рата случайной величины. Поэтому на пр

ти е для рассеивания (или отклоне-

ния) чаще используют характеристи у, совп д ющую по размерности со слу-

чайной величиной, – это среднее квадратич с ое отклонение.

Средним квадратическим отклон ни м называется положительное значе-

ние квадратного корня из дисперсии случайной величины X, которое обозначается

как x :

x D[X].

(4.12)

Свойства д сперс

1. Дисперсия постоянной величины (C const) равна нулю:

D C 0.

Доказательствоб

математического ожидания) из определе-

Так как M C C (свойство 1

ния дисперсии (4.9), подставляя X = C, получаем

D C M C M C

M C C

2.Постоянный множитель выносится за знак дисперсии и возводится в квадрат:

D CX C2D X .

Доказательство:

D CX M CX M CX 2 M CX CM X 2

M C2 X M X 2 C2M X M X 2 C2D X .

3. Дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:

D X M

Доказательство:

D X M X M X 2 M

X2 2XM

X M X 2

2M X M X M

M X .

4. Для независимых случайных величин дисперсия суммыИили разности

случайной величины равна сумме дисперсии:

D[X Y] D[X] D[Y].

Доказательство:

Y M Y

D X Y M

X Y M X

X M X

раскроем квадрат двухв личин,стоящих в круглых скобках

M X M X

2 X

X Y M Y Y M Y

ема

используя свойства ма

ического ожидания,

найдем математическ е ожидание откаждого слагаемого

случайной

Y M Y

величины независимы, то

X M X

Y M Y

D X D Yи2M

Если

Y M Y

M X M X M Y M Y 0.

X M X

Окончательно получаем:

D X Y D X D Y .

5. Дисперсия произведения независимых случайных величин

D[X Y] D[X] D[Y] mx

2D[Y] my2D[X].

(4.13)

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 249 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.04.2019176.6 Кб4АИАС Экзамен.docx
#
15.04.2019172.66 Кб13АиАС.docx
#
11.05.2015347.62 Кб4АКВАРиУМ ПОД ПРИПЯТЬЮ.docx
#
11.05.2015148.48 Кб37АКГ контроша.doc
#
11.05.20151.74 Mб59АКГ лекции.doc
#
17.03.20161.92 Mб33Аксенчик А. В. - Теория вероятностей и мат статистика. Уч. мет. пос.pdf
#
11.05.2015362.74 Кб39алгоритмы и блок-схемы.pdf
#
11.05.20151.15 Mб48Алгоритмы_вычислит_математики_Уч_мет_пос.pdf
#
11.05.2015200.29 Кб41алёшкина).docx
#
20.08.201988.59 Кб4АНАЛИЗ СПРОСА И ПРЕДЛОЖЕНИЯ.docx
#
20.08.201932.99 Кб5АНАЛИЗ ТИПОВ РЫНОЧНЫХ СТРУКТУР.docx