
Алгоритмы C++
.pdf
с умножением.
Виды дробной длинной арифметики
Операции над дробными числами встречаются гораздо реже, и работать с огромными дробными числами значительно сложнее, поэтому в олимпиадах встречается только специфическое подмножество дробной длинной арифметики.
Длинная арифметика в несократимых дробях
Число представляется в виде несократимой дроби , где 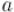 и
и 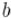 — целые числа. Тогда все операции над дробными числами нетрудно свести к операциям над числителями и знаменателями этих дробей.
— целые числа. Тогда все операции над дробными числами нетрудно свести к операциям над числителями и знаменателями этих дробей.
Обычно при этом для хранения числителя и знаменателя приходится также использовать длинную арифметику, но, впрочем, самый простой её вид — Классическая длинная арифметика, хотя иногда достаточно применения для них 64-битного встроенного типа.
Выделение позиции плавающей точки в отдельный тип
Иногда в задаче требуется производить расчёты с очень большими либо очень маленькими числами, но при этом не допускать их переполнения. Встроенный 8-байтовый тип double, как известно, допускает значения экспоненты в диапазоне  , чего иногда может оказаться недостаточно.
, чего иногда может оказаться недостаточно.
Приём, собственно, очень простой — вводится ещё одна целочисленная переменная, отвечающая за экспоненту, а
после выполнения каждой операции дробное число "нормализуется", т.е. возвращается в отрезок |
, |
путём увеличения или уменьшения экспоненты. |
|
При перемножении или делении двух таких чисел надо соответственно сложить либо вычесть их экспоненты. При сложении или вычитании перед выполнением этой операции числа следует привести к одной экспоненте, для чего одно из них домножается на 10 в степени разности экспонент.
Наконец, понятно, что не обязательно выбирать 10 в качестве основания экспоненты. Исходя из устройства встроенных типов с плавающей точкой, самым выгодным представляется класть основание равным 2.

Дискретное логарифмирование
Задача дискретного логарифмирования заключается в том, чтобы по данным целым 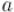 ,
, 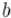 ,
, 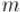 решить уравнение:
решить уравнение:
где 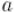 и
и  — взаимно просты (примечание: если они не взаимно просты, это конечно не означает, что решений нет или находить их легко; просто в этом случае описанный ниже алгоритм является некорректным).
— взаимно просты (примечание: если они не взаимно просты, это конечно не означает, что решений нет или находить их легко; просто в этом случае описанный ниже алгоритм является некорректным).
Здесь описан алгоритм, известный как "baby-step-giant-step algorithm", предложенный Шэнксом (Shanks) в 1971 г., работающий за время за 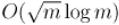 .
.
Алгоритм
Итак, имеем уравнение:
Воспользуемся для его решения методом Meet-in-the-Middle. Для этого преобразуем уравнение. Положим
где 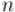 — это заранее выбранная константа, зависящая от
— это заранее выбранная константа, зависящая от 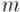 . Иногда
. Иногда 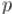 называют "giant step" (поскольку увеличение его на единицу увеличивает
называют "giant step" (поскольку увеличение его на единицу увеличивает 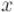 сразу на
сразу на 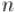 ), а в противоположность ему
), а в противоположность ему 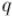 — "baby step".
— "baby step".
Очевидно, что любое (а мы рассматриваем только |
) можно представить в такой форме, причём для |
этого будет достаточно значений: |
|
|
|
|
|
Тогда уравнение принимает вид:

откуда, пользуясь тем, что 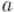 и
и 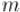 взаимно просты, получаем:
взаимно просты, получаем:
Чтобы решить исходное уравнение, нужно найти соответствующие значения 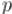 и
и  , чтобы значения левой и правой частей совпали. Иначе говоря, надо решить уравнение:
, чтобы значения левой и правой частей совпали. Иначе говоря, надо решить уравнение:
Эта задача решается с помощью метода Meet-in-the-Middle следующим образом. Посчитаем значения функции
для всех значений аргумента 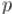 , и отсортируем эти значения. Затем будем перебирать значение второй переменной
, и отсортируем эти значения. Затем будем перебирать значение второй переменной 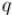 , вычислять вторую функцию , и искать это значение среди предвычисленных значений первой функции с
, вычислять вторую функцию , и искать это значение среди предвычисленных значений первой функции с
помощью бинарного поиска.
Асимптотика
Сначала оценим время вычисления каждой из функций |
и |
. И та, и другая содержит возведение в |
степень, которое можно выполнять с помощью алгоритма бинарного возведения в степень. Тогда функцию мы можем вычислить за время 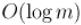 , а
, а 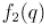 — за время
— за время 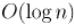 .
.
Сам алгоритм в первой части содержит вычисление функции |
для каждого возможного значения и |
дальнейшую сортировку значений, что даёт нам асимптотику: |
|
|
|
|
|
Во второй части алгоритма происходит вычисление функции |
для каждого возможного значения и бинарный |
поиск по массиву значений , что даёт нам асимптотику: |
|
|
|
|
|
Теперь, когда мы сложим эти две асимптотики, практически очевидно, что минимум достигается, когда |
, т. |
е. для оптимальной работы алгоритма константу следует выбирать равной: |
|
|
|
|
|
При таком выборе асимптотика алгоритма принимает вид:
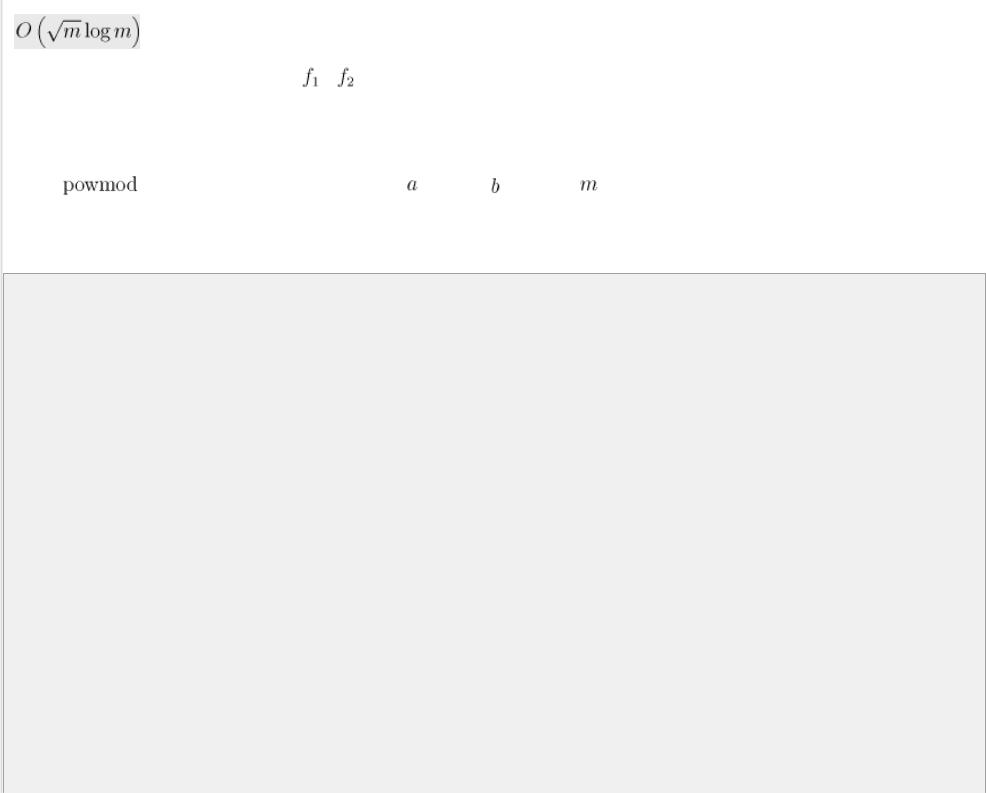
|
|
|
|
Примечание. Мы могли бы обменять ролями |
и |
(какую сортировать и затем выполнять по ней бинарный |
|
поиск), однако результат от этого не изменится. |
|
|
|
Реализация |
|
|
|
Функция |
выполняет бинарное возведение числа в степень по модулю , см. Бинарное возведение |
||
в степень. |
|
|
|
Функция 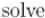 производит собственно решение задачи.
производит собственно решение задачи.
int powmod (int a, int b, int m) { int res = 1;
while (b > 0) if (b & 1)
res = (res * a) % m, --b;
else
a = (a * a) % m, b >>= 1; return res;
}
int solve (int a, int b, int m) {
int msq = (int) sqrt (m + .0) + 1;
int msq2 = m / msq + (m % msq ? 1 : 0); vector < pair<int,int> > vals (msq2); for (int i=1; i<=msq2; ++i)
vals[i-1] = make_pair (powmod (a, i * msq, m), i); sort (vals.begin(), vals.end());
for (int i=0; i<=msq; ++i) {
int cur = powmod (a, i, m); cur = (cur * b) % m;
vector < pair<int,int> > ::iterator it =
lower_bound (vals.begin(), vals.end(), make_pair (cur, 0)); if (it != vals.end() && it->first == cur)
return it->second * msq - i;
}

return -1;
}

Линейные диофантовы уравнения с двумя переменными
Диофантово уравнение с двумя неизвестными имеет вид:
где 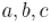 — заданные целые числа,
— заданные целые числа,  и
и 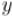 — неизвестные целые числа.
— неизвестные целые числа.
Ниже рассматриваются несколько классических задач на эти уравнения: нахождение любого решения, получение всех решений, нахождение количества решений и сами решения в определённом отрезке, нахождение решения с наименьшей суммой неизвестных.
Вырожденный случай
Один вырожденный случай мы сразу исключим из рассмотрения: когда . В этом случае, понятно, уравнение имеет либо бесконечно много произвольных решений, либо же не имеет решений вовсе.
Нахождение одного решения
Найти одно из решений диофантова уравнения с двумя неизвестными можно с помощью Расширенного алгоритма Евклида.
Расширенный алгоритм Евклида по заданным 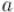 и находит их наибольший общий делитель , а также такие коэффициенты
и находит их наибольший общий делитель , а также такие коэффициенты 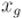 и
и 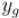 , что:
, что:
|
|
|
Утверждается, что если делится на |
, то диофантово уравнение |
имеет решение; |
в противном случае диофантово уравнение решений не имеет. Доказательство следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.
Предположим, что 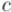 делится на
делится на 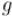 , тогда, очевидно, выполняется:
, тогда, очевидно, выполняется:
т.е. одним из решений диофантова уравнения являются числа:

Получение всех решений
Покажем, как получить все остальные решения (а их бесконечное множество) диофантова уравнения, зная одно из решений  .
.
Итак, пусть 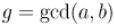 , а числа
, а числа 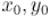 удовлетворяют условию:
удовлетворяют условию:
Тогда заметим, что, прибавив к 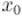 число
число 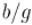 и одновременно отняв
и одновременно отняв 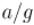 от
от 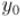 , мы не нарушим равенства:
, мы не нарушим равенства:
Очевидно, что этот процесс можно повторять сколько угодно, т.е. все числа вида:
являются решениями диофантова уравнения.
Более того, только числа такого вида и являются решениями, т.е. мы описали множество всех решений диофантова уравнения (оно получилось бесконечным, если не наложено дополнительных условий).
Нахождение количества решений и сами решения в заданном отрезке
Пусть даны два отрезка |
и |
, и требуется найти количество решений |
диофантова |
|
уравнения, лежащих в данных отрезках соответственно. |
|
|
||
Заметим, что если одно из чисел |
равно нулю, то задача имеет не больше одного решения, поэтому эти случаи мы |
|||
в данном разделе исключаем из рассмотрения. |
|
|
||
Сначала найдём решение с наименьшим |
таким, что |
. Для этого сначала найдём |
||
любое решение диофантова уравнения (см. пункт 1). Затем получим из него решение с наименьшим 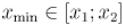

— воспользуемся процедурой, описанной в предыдущем пункте, и будем уменьшать/увеличивать 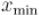 , пока оно не попадёт в заданный отрезок, и при этом будет наименьшим. Это можно сделать за
, пока оно не попадёт в заданный отрезок, и при этом будет наименьшим. Это можно сделать за 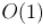 таким образом:
таким образом:
int
a, b, c, g, // коэффициенты диофантова уравнения, и g=gcd(a,b) x0, y0, // одно из решений диофантова уравнения
x1, x2, // заданный отрезок
mx, my; // искомое решение с наименьшим x >= x1 int cnt = (x1 - x0) / b;
if (x0 + cnt * b < x1) ++cnt;
mx = x0 + cnt * b; my = y0 - cnt * b;
Здесь предполагается, что  (если
(если 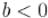 , то нужно предварительно изменить знаки
, то нужно предварительно изменить знаки 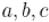 ). Аналогичным образом найдём решение с наибольшим
). Аналогичным образом найдём решение с наибольшим 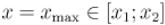 .
.
Теперь, если |
|
, то количество решений равно нулю. |
|
|
|
Если же |
|
, то нам осталось наложить условие на : |
. |
|
|
Пусть |
и |
— это соответствующие решения для |
и |
. Если |
, |
то обменяем их местами. Теперь нам нужно найти пересечение отрезка |
и |
. Будем |
|
||
увеличивать |
(на |
), пока оно не станет больше либо равно , и будем уменьшать |
(опять же, на |
||
), пока оно не станет меньше либо равно . После этого посчитаем для каждого из полученных |
и |
||||
значения решений , и если хотя бы одно из них не попало в отрезок |
, то задача решений не имеет. |
||||
Иначе же, ответом на задачу будет являться величина |
. |
|
|
||
Таким образом, мы можем найти количество решений в заданном отрезке за |
|
, а также вывести |
|||
все решения за время, пропорциональное их количеству.
Нахождение решения в заданном отрезке с наименьшей суммой x+y
Здесь на 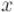 и на
и на 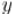 также должны быть наложены какие-либо ограничения, иначе ответом практически всегда будет минус бесконечность.
также должны быть наложены какие-либо ограничения, иначе ответом практически всегда будет минус бесконечность.
Идея решения такая же, как и в предыдущем пункте: сначала находим любое решение диофантова уравнения, а

затем, применяя описанную в предыдущем пункте процедуру, придём к наилучшему решению. Действительно, мы имеем право выполнить следующее преобразование (см. предыдущий пункт):
Заметим, что при этом сумма 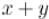 меняется следующим образом:
меняется следующим образом:
|
|
|
Т.е. если |
, то нужно выбрать как можно меньшее значение , если |
, то нужно выбрать как можно |
большее значение . |
|
|
Если |
, то мы никак не сможем улучшить решение, — все решения будут обладать одной и той же суммой. |
|
Таким образом, мы решили эту задачу за асимптотику |
. |
|

Модульное линейное уравнение первого порядка
Постановка задачи
Это уравнение вида:
где 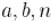 — заданные целые числа,
— заданные целые числа, 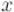 — неизвестное целое число.
— неизвестное целое число.
Требуется найти искомое значение , лежащее в отрезке |
(поскольку на всей числовой прямой, ясно, |
|
может существовать бесконечно много решений, которые будут отличаться друг друга на |
, где — любое |
|
целое число). Если решение не единственно, то мы рассмотрим, как получить все решения. |
|
|
Решение с помощью нахождения Обратного элемента
Рассмотрим сначала более простой случай — когда 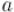 и
и 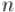 взаимно просты. Тогда можно найти обратный элемент к числу
взаимно просты. Тогда можно найти обратный элемент к числу 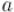 , и, домножив на него обе части уравнения, получить решение (и оно будет единственным):
, и, домножив на него обе части уравнения, получить решение (и оно будет единственным):
Теперь рассмотрим случай, когда 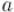 и
и 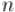 не взаимно просты. Тогда, очевидно, решение будет существовать не всегда (например,
не взаимно просты. Тогда, очевидно, решение будет существовать не всегда (например, 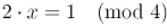 ).
).
Пусть 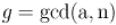 , т.е. их наибольший общий делитель (который в данном случае больше единицы).
, т.е. их наибольший общий делитель (который в данном случае больше единицы).
Тогда, если не делится на , то решения не существует. В самом деле, при любом |
левая часть уравнения, т. |
|
е. |
, всегда делится на , в то время как правая часть на него не делится, откуда и следует, |
|
что решений нет. |
|
|
Если же делится на |
, то, разделив обе части уравнения на это (т.е. разделив , |
и на ), мы придём к |
новому уравнению: |
|
|
|
|
|
|
|
|
