2. Формула Стокса

Литература. [4], гл. XV, § 7, упр. 31—33; [5], гл. VII, § 10 (п. 3°), § 12 (п. 5°), задачи 2357—2359; [9], ч. II, гл. II, § 6.

П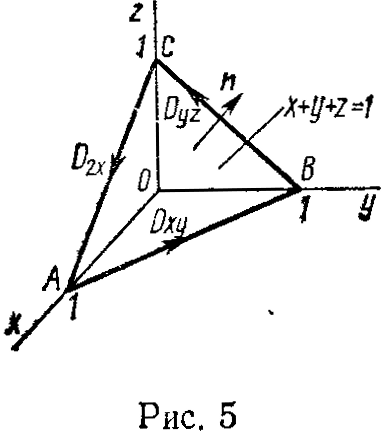ример 2. Найти циркуляцию векторного поля F=(х-2z)i+(x+3y+z)j+(5х+у)k по контуру треугольника ABC; где A(1; 0; 0), В(0; 1; 0), С(0; 0; 1) (рис. 5).

Решение. Используем формулу Стокса

где направление обхода контура λ должно быть положительным. Находим:

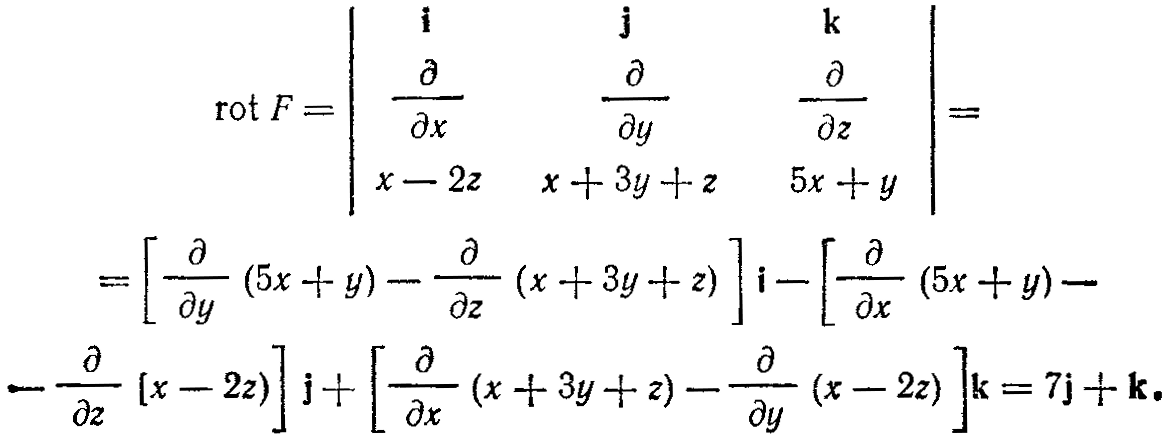
В качестве о возьмем треугольник ABC, который расположен на плоскости х+у+z=1; берем верхнюю сторону этого треугольника (нормальный вектор n выходит из выбранной стороны поверхности; см. рис. 5).

По формуле (3) последовательно находим (к — контур треугольника ABC; направление обхода по К указано на рис. 5):

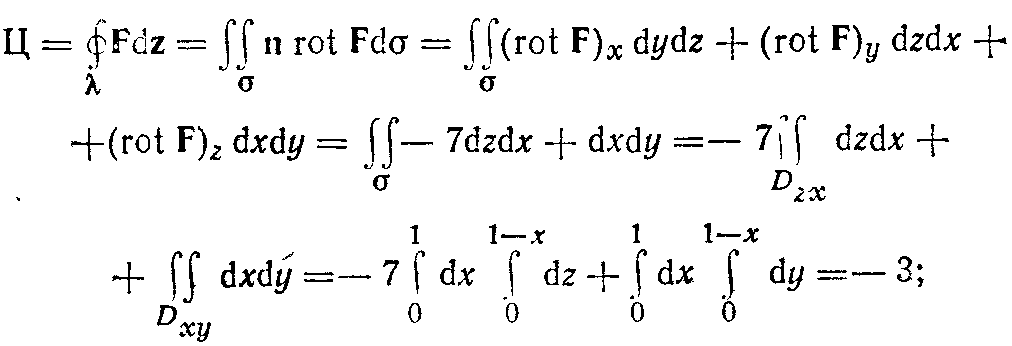
здесь (rot F)_x, (rot F)_y, (rot F)_z — координаты вектора rot F, т. е, его проекции на оси координат.

3. Формула Остроградского

Литература. [4], гл. XV, § 8, упр. 34—41; [5], гл. VII, § 11, 12 (п. 4), задачи 2363—2367; [9], ч. II, гл. II, § 6.

Пример 3. Найти поток векторного поля P=х²_i+x_j+x_zk через внешнюю сторону замкнутой поверхности σ, расположенной в первом октанте и образованной частями параболоида вращения у=z²+x² и следующих плоскостей: у=1, х=0, z=0 (см. рис. 4).

Решение. Используем формулу Остроградского

где n — внешняя нормаль поверхности σ. Находим

По формуле (4) получаем

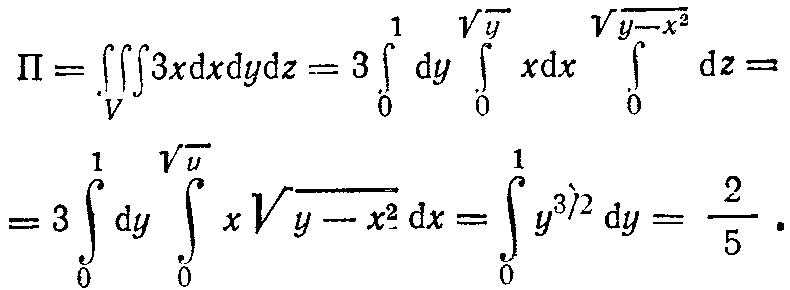
4. Потенциальные и соленоидальные векторные поля

Литература. [4], гл. XV, § 9, п. 4, о; [5], гл. VII, § 12 '(п. 6°), задачи 2397—2400.

Векторное поле F=Xi+Yj+Zk называется потенциальным, если F = grad u, где u=u(х, у, z)—скалярная функция (потенциал поля). Потенциал поля обычно находят по формуле

г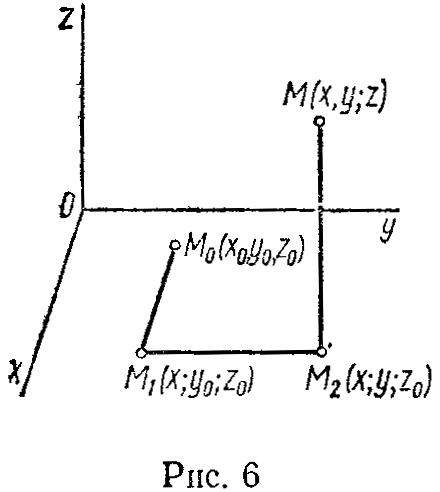де M₀(x₀; y₀; z₀) - фиксирования точка рассматриваемой области.

Формула (5) получается в результате вычисления интеграла

по ломаной M₀M₁M₂M (рис. 6), звенья которой параллельны осям координат (предполагается, что эта ломаная принадлежит рассматриваемой односвязной области).

является потенциальным. Найти его потенциал.

Решение. Находим

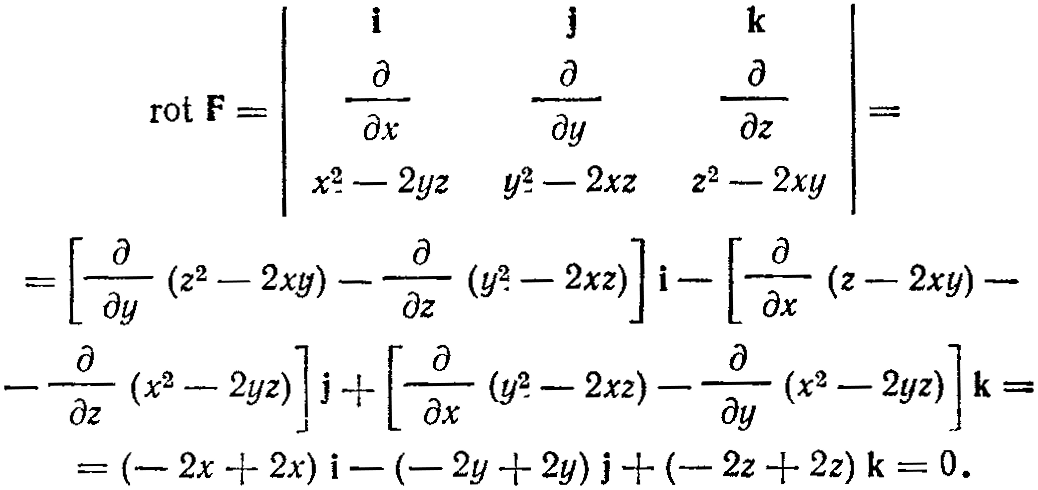
Отсюда следует, что данное поле — потенциальное.

Потенциал поля и(x, у, г) находим по формуле (5):

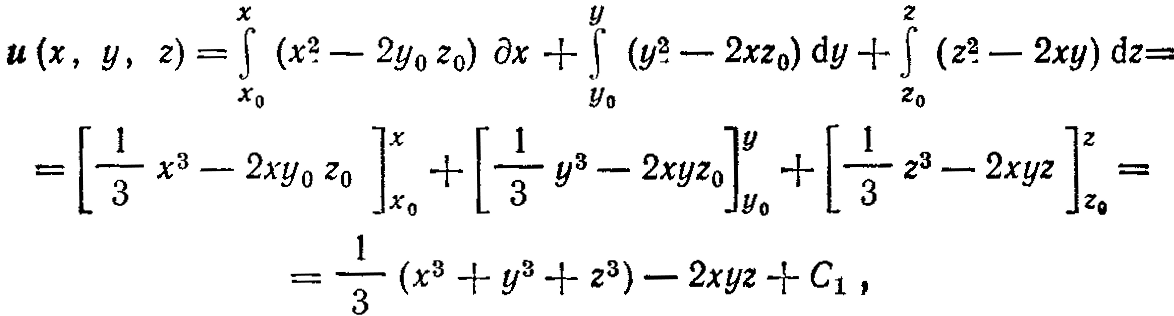
где

Векторное поле F называется соленоидальным, если в каждой точке поля divF=0. Так, например, векторное поле

является соленоидальным, так как для него

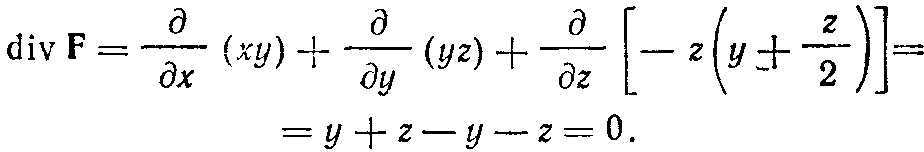
5. Операторы Гамильтона и Лапласа

Литература. [4], гл. XV, § 9, упр. 20, 43; [5], гл. VII, § 12, п 2°, 6°.

Дополнительные сведения по векторному анализу можно найти в пособии: Смирнов В. И. Курс высшей математики. — М.: Наука, 1974, т. II, гл. IV, § 11.

Вопросы для самопроверки

1. Выведите формулу Стокса и напишите ее в векторной форме.

2. Выведите формулу Остроградского и напишите ее в векторной форме.

3. Какое поле называется потенциальным? Что такое потенциал этого поля? В чем состоит необходимое и достаточное условие потенциальности поля?

4. Напишите формулу для нахождения потенциала U(x, у, z) потенциального поля F=Xdx+Ydy+Zdz. Приведите пример применения этой формулы.

5. Какое поле называется соленоидальным? Приведите пример.

6. Какая функция называется гармонической? Приведите пример.

7. Что такое оператор Гамильтона? Обоснуйте записи: .

8. Докажите, что rot(grad u)=0. Запишите это равенство с помощью оператора Гамильтона.

9. Что называется оператором Лапласа? Выведите формулу

10. Что называется уравнением Лапласа? Как называется функция, удовлетворяющая этому уравнению?

11. Запишите оператор Лапласа в цилиндрических и сферических координатах.

После изучения тем XV, XVI и XVII выполните контрольную работу 9.