Двойственные функции

Симметрия элементов 0 и 1 в множествеBприводит к понятию двойственности.

Определение 4 (Двойственная функция). Функцияg(x₁,...,x_n)= ¬f(¬x₁,...,¬x_n) называетсядвойственной функциейк функцииfи обозначаетсяf^*.

Пример 2 (двойственные функции).

(x & y)^* = ¬(¬x & ¬y) = x  y.



Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f^*(x₁,...,x_n)^* = (¬f(¬x₁,...,¬x_n))^* =^*= ¬¬f(¬¬x₁,...,¬¬x_n) =^*=f(x₁,...,x_n)^*



Рассмотрим, что происходит с таблицей двойственной функции. Замена набора (x₁,...,x_n) на (¬x₁,...,¬x_n) соответствует ``переворачиванию'' таблицы. Действительно, наборы (x₁,...,x_n) и (¬x₁,...,¬x_n) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию¬к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & yиx  y, задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являютсяx  yиx  y, задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функцийxи¬x(векторы (0,1) и (1,0) соответственно) двойственна сама себе.



Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее:

f₀(f₁,...,f_m)^* = f₀^*(f₁^*,...,f_m^*)

Доказательство. f₀(f₁(x₁,...,x_n),...,f_m(x₁,...,x_n))^* =

= ¬f0(f1(¬x1,...,¬xn),...,fm(¬x1,...,¬xn)) =	*
= ¬f0(¬¬f1(¬x1,...,¬xn),...,¬¬fm(¬x1,...,¬xn)) =	*
= ¬f0(¬f1*(x1,...,xn),...,¬fm*(x1,...,xn)) =	*
= f0*(f1*(x1,...,xn),...,fm*(x1,...,xn))	*

----7----

7 «Алгоритм — это система операторов, взятых из множества операторов некоторого исполнителя, которая полностью определяет некоторый класс алгоритмических процессов, то есть процессов, которые:

дискретны;

детерминированы;

потенциально конечны;

преобразовывают некоторые конструктивные объекты.

Между операторами алгоритма и операциями (элементарными действиями) алгоритмического процесса существует гомоморфное соответствие. Поэтому алгоритм следует также считать моделью алгоритмического процесса»

Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:

детерминированность — определённость. В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа.

понятность — алгоритм для исполнителя должен включать только те команды, которые ему (исполнителю) доступны, которые входят в его систему команд.

завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов. С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.

массовость — алгоритм должен быть применим к разным наборам исходных данных.

Важную роль играют рекурсивные алгоритмы (алгоритмы, вызывающие сами себя до тех пор, пока не будет достигнуто некоторое условие возвращения). В последнее время активно разрабатываются параллельные алгоритмы, предназначенные для вычислительных машин, способных выполнять несколько операций одновременно

----8---

. Граф – это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек.

Вершины, прилегающие к одному и тому же ребру, называются смежными.

Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным.

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра – линиями, соединяющими точки.

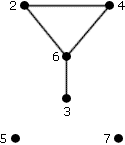
Пример 1 (граф)

Петля – это дуга, начальная и конечная вершина которой совпадают.

Простой граф – граф без кратных ребер и петель.

Степень вершины – это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

----9----

Пути, маршруты, цепи и циклы

Путь в ориентированном графе – это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Вершины v0, vn называются связанными данным путем (или просто связанными). Вершину v0 называют началом, vn – концом пути. Если v0 = vn, то путь называют замкнутым. Число n называется длиной пути.

Маршрут в графе – путь, ориентацией дуг которого можно пренебречь.

Цепь – маршрут, в котором все ребра попарно различны.

Цикл – замкнутый маршрут, являющийся цепью.

Маршрут, в котором все вершины попарно различны, называют простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называются простым циклом.

Пример 2 (граф отношения делимости)

П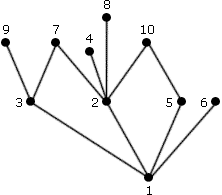остроим граф, изображающий отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}. Принцип такой: если от одного числа до другого есть цепь, ведущая вверх, тогда второе число делится на первое.

---10---