
Васюков В_Н_ Теория электрической связи_
.pdf
Упражнения |
103 |
20.Для чего частоту дискретизации на практике выбирают больше удвоенной верхней частоты спектра сигнала?
21.Для чего перед дискретизацией аналоговый сигнал подвергают НЧ-фильтрации?
22.Что такое аналитический сигнал? Как связаны вещественный сигнал и соответствующий ему аналитический сигнал?
УПРАЖНЕНИЯ
1. Выведите из (2.5) представление сигнала, отличного от нуля на всей вещественной оси.
2. Докажите, что в линейном пространстве должно выпол-
няться условие
0 : x M :0x 0.
3.Докажите линейную независимость функций, упомянутых
впримере 2.1.
4.Рассчитайте первые 8 функций Уолша согласно рекуррентным выражениям примера 2.11 и постройте их графики (выполните это задание для функций Уолша, заданных на интервалах (–0,5; 0,5) и (0; 1)). Сравните полученные результаты.
5.Запишите обобщенную формулу Рэлея для пространств L2 и l2 .
6. Докажите самосопряженность ядра Гильберта |
1 |
. |
(s t) |
7. Докажите свойство дуальности (2.48) преобразования Фурье.
8. Объясните качественно присутствие -функции в выраже-
нии (2.51).
9.Докажите свойство (2.54).
10.Выведите формулу, приведенную в примере 2.20.
11.Докажите, что АКФ вещественного сигнала обладает свойством четности.
12.Найдите выражение АКФ прямоугольного видеоимпульса (пример 2.22) на основании общего выражения (2.53)
13.Убедитесь, что импульсная характеристика идеального ин-
терполирующего |
фильтра с КЧХ (2.60) имеет вид h(t) |
|||||
|
|
|
|
|||
sin |
|
t |
|
|
|
t . |
|
|
|||||
Td |
|
Td |
|
|||
14. Часто в качестве моделей импульсных сигналов используют нефинитные функции, имеющие бесконечную длительность.

104 |
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ |
В таких случаях вводят эффективную длительность сигнала – временной интервал, на котором сосредоточена бόльшая часть его энергии. Определите эффективную длительность экспоненциального импульса
|
|
t |
, t |
|
0 |
|
Ae |
|
|
, |
|||
s(t) |
0, |
|
t |
|
0 |
|
|
|
|
||||
как интервал, на котором сосредоточено 95 % энергии.
15. Многие модели сигналов, удобные в аналитическом отно-
шении, характеризуются нефинитным спектром (или спектральной плотностью). Для них вводят понятие эффективной ширины спек-
тра – частотного интервала, содержащего заданную долю kэ энер-
гии сигнала. Определите эффективную ширину спектра прямоугольного импульса при kэ 0.9664 .

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
ак отмечалось в разд. 1, все сигналы и помехи Кявляются случайными, т. е. непредсказуемы-
ми. Математическими моделями случайных сигналов и помех служат случайные процессы. В терминах современной теории вероят-
ностей всякий случайный процесс (СП) связан с некоторым вооб-
ражаемым множеством, или пространством элементарных событий . Выбор одного из элементарных событий проис-
ходит некоторым способом, который наблюдателю не известен и представляется случайным, поэтому исход такого эксперимента
заранее предсказать нельзя. Выбор конкретного элемента приводит к осуществлению вполне определенной реализации случай-
ного процесса. Важно подчеркнуть, что в основе теории вероятностей лежит допущение о возможности многократного повторения случайного эксперимента в одинаковых условиях и получения любого количества реализаций случайного события, случайной ве-
личины или |
случайного процесса. С пространством |
связана |
функция P : |
, называемая вероятностной мерой (распреде- |
|
лением вероятностей), в соответствии с которой элементарные события имеют бóльшие или меньшие шансы быть выбранными в конкретном опыте. Более точно, мера P ставит в соответствие любому подмножеству A множества неотрицательное вещественное число, не превышающее единицы, называемое вероятностью
P(A) случайного события A . При этом P( ) 1 , т. е. вероятность
достоверного события равна 1. Невозможное событие, обозначаемое , имеет вероятность P( ) 0 . Строго говоря, в современной
теории вероятностей для полного задания вероятностного описания необходимо также определить систему измеримых подмножеств (подмножеств множества , для которых определена мера), замкнутую относительно операций объединения и пересечения и называемую -алгеброй или -полем.

106 |
3. СЛУЧАЙНЫЕ ПРОЦЕССЫ |
Теория случайных процессов представляет собой большой раздел теории вероятностей, который изучается в курсе математики, поэтому здесь приводится лишь краткое изложение основных понятий, необходимых для понимания изучаемых разделов теории электрической связи. Для более полного изучения теории вероятностей и теории случайных процессов следует обратиться к специальным учебникам, например [6, 7].
3.1.СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ИИХ ХАРАКТЕРИСТИКИ
Случайной величиной (СВ) называется любая функция x( ) ,
определенная на множестве |
и принимающая вещественные зна- |
|
чения48. При фиксированном |
|
значение x x( ) также фик- |
сировано; оно называется реализацией случайной величины x . Далее для краткости случайные величины обозначаются так же, как и их реализации, если это не приводит к двусмысленности.
Полное описание случайной величины составляет кумулятивная функция распределения, определяемая выражением
F(a) P x x( ) a ,
где P{} обозначает вероятность события, состоящего в том, что
случайная величина принимает значение, не превосходящее заданного значения a . Случайная величина, принимающая значения из
дискретного множества, называется дискретной. Функция распределения такой СВ имеет ступенчатый вид. Если функция распреде-
ления является непрерывной и дифференцируемой, то можно оп-
ределить плотность распределения вероятностей (ПРВ),
называемую также для краткости плотностью вероятности (а иногда просто плотностью)
|
x |
w(x) dF(x) , при этом F(x) w(x)dx . |
|
dx |
|
Очевидно, функция распределения по определению должна |
|
быть неотрицательной неубывающей |
функцией со свойствами |
48Комплексная случайная величина определяется парой вещественных случайных величин, рассматриваемых совместно и играющих роль вещественной и мнимой частей комплексной СВ.

3.1. Случайные величины и их характеристики |
107 |
|
F( ) 0 , |
F( ) 1. Следовательно, |
плотность распределения |
должна быть неотрицательной функцией, удовлетворяющей усло-
вию нормировки w(x)dx 1.
Иногда используется описание случайной величины характеристической функцией, которая определяется выражением
(u) w(x)e juxdx ,
совпадающим с преобразованием Фурье плотности распределения вероятностей (с точностью до знака показателя экспоненты).
Иногда нет необходимости использовать полное описание случайной величины и можно ограничиться ее числовыми характеристиками. Чаще всего этими характеристиками служат так называемые моменты, определяемые следующими выражениями. Начальный момент k -го порядка ( k -й начальный момент)
|
|
|
|
m |
xk w(x)dx xk E xk , |
||
k |
|
|
|
|
|
||
где горизонтальная черта и E – символические обозначения ин-
тегрального оператора усреднения по ансамблю49. Наиболее часто используется первый начальный момент
|
|
|
m m1 |
xw(x)dx x , |
(3.1) |
называемый математическим ожиданием, или центром распределения50. Смысл этого понятия становится яснее из физической аналогии: если плотность распределения вероятностей рассматривать как линейную плотность бесконечно тонкого стержня единичной массы, расположенного вдоль оси абсцисс, то математическое ожидание будет равно координате центра масс этого стержня.
49Под ансамблем понимается множество реализаций случайной величины или процесса вместе с вероятностной мерой, заданной на этом множестве.
50Часто употребляется также термин «среднее», например, типично выражение «случайный процесс с нулевым средним».
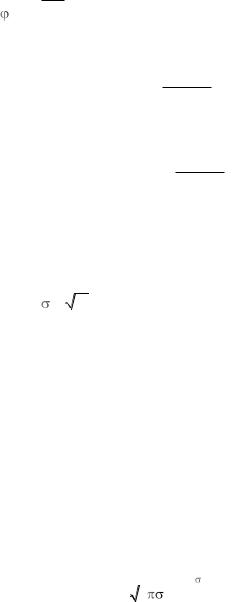
108 |
3. СЛУЧАЙНЫЕ ПРОЦЕССЫ |
Отметим, что усреднение по ансамблю можно применять к любой функции случайной величины; так, характеристическую функцию можно трактовать как результат усреднения комплексной экс-
поненты (u) e jux .
Центральный момент k -го порядка ( k -й центральный момент) равен k -му начальному моменту центрированной случайной величины (x m) :
Mk (x m)k w(x)dx (x m)k E{(x m)k } .
Наиболее употребительным из центральных моментов является второй центральный момент, или дисперсия
D M2 (x m)2 w(x)dx (x m)2 E{(x m)2} . (3.2)
В упомянутом выше механическом примере дисперсии соответствует момент инерции стержня при вращении его вокруг центра масс. Дисперсия тем меньше, чем более сосредоточена «масса вероятности» около среднего значения случайной величины (математического ожидания). Вместо дисперсии часто оперируют вели-
чиной, равной  D и называемой среднеквадратическим отклонением (СКО) случайной величины.
D и называемой среднеквадратическим отклонением (СКО) случайной величины.
Еще одной числовой характеристикой СВ является средний
|
|
|
|
|
квадрат, или второй начальный момент m |
|
x2w(x)dx x2 |
||
2 |
|
|
|
|
|
|
|
|
|
E{x2}. Нетрудно видеть, что он связан с дисперсией и математическим ожиданием:
|
|
D (x m)2 w(x)dx (x2 2mx m2 )w(x)dx |
|
|
|
m 2m2 |
m2 m m2 . |
2 |
2 |
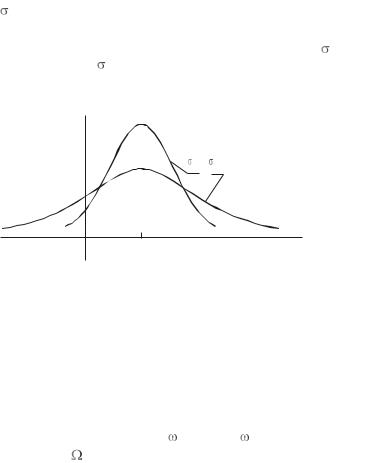
Пример 3.1. В математике и технике часто используется нормальное, или гауссово (гауссовское), распределение с ПРВ
|
|
1 |
|
|
(x m)2 |
|
w(x) |
|
|
e |
2 2 , |
||
|
|
|
||||
2 |
||||||
|
|
|
|
|
3.1. Случайные величины и их характеристики |
109 |
где m и – параметры распределения. Подставив эту плотность в (3.1) и (3.2), можно убедиться, что математическое ожидание гаус-
совской случайной величины равно m , а дисперсия равна 2 . Таким образом, параметр имеет смысл СКО и характеризует степень «размазанности» распределения (рис. 3.1). ◄
w(x) |
|
1< |
2 |
m |
x |
Рис. 3.1. Гауссовские ПРВ при различных значениях |
|
СКО |
|
В теории информации используется числовая характеристика
распределения случайной величины, называемая (дифференциальной) энтропией и определяемая выражением
|
|
|
|
|
|
|
1 |
||
H (x) log2 |
w(x)log2 w(x)dx . |
|||
w(x) |
||||
|
|
|
||
Две случайные величины x x( ) и y y( ) , заданные на об-
щем пространстве , характеризуются совместной плотностью распределения w(x, y) . Числовыми характеристиками совместной
плотности служат начальные и центральные смешанные моменты
|
|
|
m |
|
|
xk ynw(x, y)dxdy , |
|
|
|
|
|
|
|||
|
|
|
kn |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
(x m )k (y m |
)n w(x, y)dxdy , |
||
kn |
|
|
|||||
|
|
|
|
x |
y |
|
|
где k и n – произвольные целые положительные числа.

110 |
3. СЛУЧАЙНЫЕ ПРОЦЕССЫ |
|
Наиболее часто используются смешанные моменты второго |
||
порядка – начальный (корреляционный момент) |
|
|
|
|
|
m11 |
xyw(x, y)dx dy kxy |
(3.3) |
|
|
|
и центральный (ковариационный момент, или ковариация51) |
|
|
|
|
|
M11 (x mx )(y my )w(x, y)dx dy Rxy . |
(3.4) |
|
Ковариация представляет собой простейшую характеристику сте-
пени статистической (вероятностной) связи случайных величин x и y. Пример 3.2. Для пары гауссовских случайных величин дву-
мерная совместная ПРВ имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(x m )2 |
|
(x m )(x m ) |
|
(x m )2 |
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
2r |
1 1 |
2 |
2 |
|
2 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||
w(x1, x2 ) |
|
|
|
|
|
|
|
e 2(1 |
|
|
) |
1 |
|
|
|
1 |
2 |
|
|
2 |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
1 , |
2 – среднеквадратические отклонения, |
m1, m2 |
|
– матема- |
||||||||||||||||||||||||
тические ожидания, |
|
r |
– |
|
коэффициент корреляции, |
представляю- |
|||||||||||||||||||||||
щий собой нормированный ковариационный момент |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Rx x |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
(x m )(x m ) |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
r |
|
|
|
1 |
1 |
2 |
|
|
|
2 |
|
|
|
1 2 |
. ◄ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||||
|
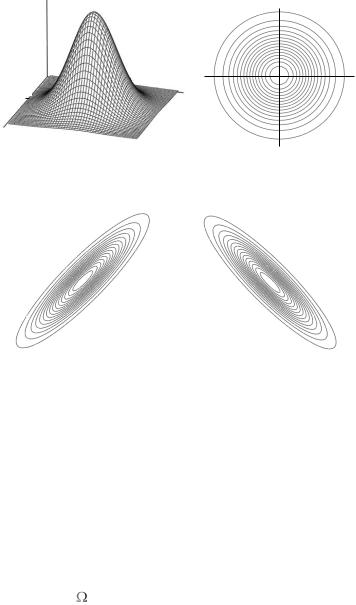
На рис. 3.2, а показана двумерная гауссовская ПРВ при r 0 , |
||||||||||||||||||||||||||||
m1 |
m2 |
0 , |
1 |
2 |
, |
а на рис. 3.2, б – |
ее отображение линиями |
||||||||||||||||||||||
уровня. Для сравнения на рис. 3.3 показаны линии уровня гауссов- |
|||||||||||||||||||||||||||||
ской ПРВ при |
r 0.9 |
(а) и r 0.9 (б). Из рисунков видно, что |
|||||||||||||||||||||||||||
при положительном коэффициенте корреляции двух СВ более вероятны их реализации с близкими значениями, а при отрицательном – с близкими по модулю, но различающимися по знаку. При нулевом коэффициенте корреляции очевидно, что
|
|
|
|
|
|
(x m )2 |
|
|
|
(x m )2 |
|
|||
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
2 |
|
w(x1 |
, x2 ) |
|
|
e |
2 |
2 |
|
|
e |
2 |
2 |
w(x1)w(x2 ) , |
||
|
|
|
1 |
|
|
|
2 |
|||||||
|
|
|
|
|
|
|||||||||
2 |
1 |
|
|
|
2 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
51В литературе иногда момент, определяемый формулой (3.3), называют ковариационным, тогда корреляционным называют момент (3.4).
3.1. Случайные величины и их характеристики |
111 |
|||||
|
|
|
|
|
|
|
|
w(x1 , x2 ) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2
0
x1
а |
|
|
|
|
б |
|||||||
Рис. 3.2. Двумерная гауссовская ПРВ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
||||||||||
|
|
|
|
|
|
|
|
x2 |
||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 3.3. Линии уровня двумерной гауссовской ПРВ при r 0,9 (а) и r 0,9 (б)
т.е. некоррелированные гауссовские случайные величины независимы (напомним, что совместная ПРВ независимых случайных величин равна произведению их одномерных ПРВ). Для негауссовских случайных величин некоррелированность не означает независимости, хотя из их независимости следует некоррелированность. Таким образом, вообще говоря, независимость – более сильное свойство, чем некоррелированность.
Поскольку случайная величина является функцией, на множестве случайных величин можно определить структуру гильбертова пространства. Действительно, случайные величины (как функции на пространстве ) можно складывать, при этом сумма снова будет случайной величиной. Случайные величины можно умножать на скалярные коэффициенты, причем множество случайных величин замкнуто относительно такого умножения. Справедливость

112 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
аксиом линейного пространства (разд. 2.3) легко проверяется непосредственно. Таким образом, множество всех вещественных случайных величин, заданных на общем множестве элементарных событий , можно рассматривать как линейное пространство над полем вещественных чисел (аналогично можно ввести пространство комплексных случайных величин над полем комплексных чисел и т.д.). Дальнейшее усовершенствование структуры пространства связано с введением нормы, метрики и скалярного произведения. Для того чтобы пространство было гильбертовым, необходимо, чтобы норма порождалась скалярным произведением, а метрика – нормой [2]. Операцию скалярного умножения определим для вещественных случайных величин x и y как смешанный
момент второго порядка (корреляционный момент)
|
|
|
|
|
|
(x, y) |
|
xyw(x, y)dxdy |
|
. |
(3.5) |
|
xy |
В частности, если две величины имеют нулевой корреляционный момент, то они являются ортогональными. Проверим выполнение аксиом скалярного произведения.
Из (3.5) очевидно выполнение равенства (x, y) (y, x) .
Проверка |
|
выполнения условия |
( x y, z) |
(x, z) (y, z) |
||||||
может быть произведена непосредственно: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( x |
y, z) |
( x |
|
y)zw(x, y, z)dxdydz |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xzw(x, z)dxdz |
|
yzw(y, z)dydz |
|
|
|
. |
||
|
|
|
xz |
yz |
||||||
|
|
|
|
|
|
|
|
|
|
|
Здесь w(x, y, z) – совместная плотность распределения вероятно-
стей трех случайных величин, которая при интегрировании по одному из аргументов дает совместную плотность оставшихся двух
случайных величин52, например w(x, y, z)dx w(y, z) .
Третье условие, очевидно, выполняется: (x, x) 0 , поскольку (x, x) – не что иное, как средний квадрат, неотрицательный по определению. Равенство нулю среднего квадрата (как второго на-
52ПРВ, которая получается интегрированием ПРВ большей размерности по одной или нескольким переменным, называется маргинальной.
