
 1ОГЛЯД
ІСНУЮЧИХ АЛГОРИТМІВ
1ОГЛЯД
ІСНУЮЧИХ АЛГОРИТМІВ
1.1 Опис алгоритмів для вирішення поставленої задачі.
1.1.1 Метод Гаусса
Він
оснований на приведенні матриці системи
до трикутного вигляду. Це досягається
послідовним виключенням невідомих з
рівнянь системи. Спочатку за допомогою
першого рівняння виключається
![]() зі
всіх наступних рівнянь системи. Потім
за допомогою другого рівняння виключається
зі
всіх наступних рівнянь системи. Потім
за допомогою другого рівняння виключається
![]() з
третього і всіх наступних рівнянь. Цей
процес, який називається прямим
ходом
метода Гаусса,
продовжується до тих пір, поки в лівій
частині останнього (
з
третього і всіх наступних рівнянь. Цей
процес, який називається прямим
ходом
метода Гаусса,
продовжується до тих пір, поки в лівій
частині останнього (
![]() -го)
рівняння не залишиться лише член з
невідомим
-го)
рівняння не залишиться лише член з
невідомим
![]() ,
тобто матриця системи не буде приведена
до трикутного вигляду. (Відмітимо, що к
такому вигляду приводиться лише
невироджена матриця. В іншому випадку
метод Гаусса застосовувати не можна.)
,
тобто матриця системи не буде приведена
до трикутного вигляду. (Відмітимо, що к
такому вигляду приводиться лише
невироджена матриця. В іншому випадку
метод Гаусса застосовувати не можна.)
Зворотній
хід метода Гаусса полягає
у послідовному обчисленні шуканих
невідомих: розв’язуючи
останнє рівняння, знаходимо єдине
невідоме
![]() .
Далі, використовуючи це значення, з
попереднього рівняння обчислюємо
.
Далі, використовуючи це значення, з
попереднього рівняння обчислюємо
![]() і
т. д. Останнім знайдемо
і
т. д. Останнім знайдемо
![]() з
першого рівняння.
з
першого рівняння.
Розглянемо застосування метода Гаусса для системи

( 1.1)
 Для
виключення
Для
виключення
![]() з
другого рівняння додамо до нього перше,
помножене на
з
другого рівняння додамо до нього перше,
помножене на
![]() .
Потім, помноживши перше рівняння на
.
Потім, помноживши перше рівняння на
![]() і
додавши результат
і
додавши результат
до
третього рівняння, також виключимо з
нього
![]() .
Отримаємо рівнозначну систему рівнянь
вигляду
.
Отримаємо рівнозначну систему рівнянь
вигляду
 (1.2)
(1.2)
Тепер
з третього рівняння системи (1.2) треба
виключити
![]() .
Для цього помножимо друге рівняння на
.
Для цього помножимо друге рівняння на
![]() і
додамо результат до третього. Отримаємо
і
додамо результат до третього. Отримаємо
 (1..3)
(1..3)
Матриця системи (1.3) має трикутний вигляд. На цьому закінчується прямий хід метода Гаусса.
Відмітимо,
що в процесі виключення невідомих
доводиться виконувати операції ділення
на коефіцієнти
![]() ,
,
![]() ,
і т. д. Тому вони мають бути відмінними
від нуля; в іншому випадку необхідно
відповідним чином переставити рівняння
системи. Переставляння рівнянь повинна
бути передбачена в обчислювальному
алгоритмі при його реалізації на ПК.
,
і т. д. Тому вони мають бути відмінними
від нуля; в іншому випадку необхідно
відповідним чином переставити рівняння
системи. Переставляння рівнянь повинна
бути передбачена в обчислювальному
алгоритмі при його реалізації на ПК.
Зворотній хід починається з розв’язання третього рівняння системи (1.3):

![]() (1..4)
(1..4)
 Використовуючи
це значення, можна знайти з другого
рівняння, а потім з першого:
Використовуючи
це значення, можна знайти з другого
рівняння, а потім з першого:
![]() (1.5)
(1.5)
Аналогічно будується обчислювальний алгоритм для лінійної системи з довільною кількістю рівнянь.
1.1.2 Метод Гаусса-Зейделя
Одним з найпоширеніших ітераційних методів, який відрізняється простотою та легкістю програмування, є метод Гаусса-Зейделя. Проілюструємо спочатку цей метод на прикладі розв’язання системи
 (1.6)
(1.6)
Припустимо,
що діагональні елементи
![]() ,
,
![]() ,
,![]() відмінні від нуля (в іншому випадку
можна переставляти рівняння). Виразимо
невідомі
відмінні від нуля (в іншому випадку
можна переставляти рівняння). Виразимо
невідомі
![]() ,
,
![]() ,
,![]() відповідного з першого, другого і
третього рівнянь системи (1.6):
відповідного з першого, другого і
третього рівнянь системи (1.6):
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
Задамо
деякі початкові (нульові) наближення
невідомих:
![]() ,
,
![]() ,
,
![]() .
Підставляючи ці значення в праву частину
виразу (1.7), отримуємо
.
Підставляючи ці значення в праву частину
виразу (1.7), отримуємо
нове
(перше) наближення для
![]() :
:
![]() (1.10)
(1.10)
Використовуючи
це значення для
![]() і
наближення
і
наближення
![]() для
для
![]() ,
знаходимо з (1.8) перше наближення для
,
знаходимо з (1.8) перше наближення для
![]() :
:
![]() (1.11)
(1.11)
І
нарешті, використовуючи обчислені
значення
![]() ,
,![]() ,
знаходимо за допомогою виразу (1.11) перше
наближення для
,
знаходимо за допомогою виразу (1.11) перше
наближення для
![]() :
:
![]() (1.12)
(1.12)
На
цьому закінчується перша ітерація
розв’язання
системи (1.7) – (1.9). Використовуючи тепер
значення
![]() ,
,
![]() ,
,
![]() ,
можна таким же чином провети
другу ітерацію, в результаті якої будуть
знайдені другі наближення до розв’язку:
,
можна таким же чином провети
другу ітерацію, в результаті якої будуть
знайдені другі наближення до розв’язку:
![]() ,
,
![]() ,
,
![]() і
т. д. Наближення з номером
і
т. д. Наближення з номером
![]() можна
представити у вигляді
можна
представити у вигляді
 (1.13)
(1.13)
Ітераційний
процес продовжується до тих пір, поки
значення
![]() ,
,
![]() ,
,
![]() не
стануть близькими з заданою похибкою
до значень
не
стануть близькими з заданою похибкою
до значень
![]() ,
,
![]() ,
,
![]() .
.
-
Метод Зейделя
Метод Зейделя є класичним ітераційним методом вирішення системи
 лінійних
рівнянь. Візьмемо систему:
лінійних
рівнянь. Візьмемо систему:
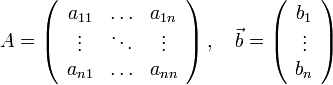 (1.14)
(1.14)
де
![]() ,
Або
,
Або
 (1.15)
(1.15)
Перепишемо
завдання у вигляді:
 (1.16)
(1.16)
Тут
в j-м-коді рівнянні ми перенесли в праву
частину всі члени, xi, що містять, для i >
j. Цей запис може бути представлений:
![]() (1.17)
(1.17)
де в прийнятих позначеннях D означає матрицю, в якої на головній діагоналі коштують відповідні елементи матриці A, а всі останні нулі; тоді як матриці U і L містять верхню і ніжнюю трикутні частини A, на головній діагоналі яких нулі. Ітераційний процес в методі Зейделя будується по формулі
![]() (1.18)
(1.18)
після вибору відповідного початкового наближення . Нові значення використовуються тут відразу ж у міру здобуття

 (1.19)
(1.19)
 де
де
![]()
Таким чином i-танучи компонента (до + 1) -го наближення обчислюється за формулою:
 (1.20)
(1.20)
Умова закінчення
ітераційного процесу Зейделя досягши
точності в спрощеній формі має вигляд:
![]() (1.21)
(1.21)
Точніша умова
закінчення ітераційного процесу має
вигляд
![]() (1.21)
(1.21)
і вимагає більше обчислень. Добре підходить для розріджених матриць.
