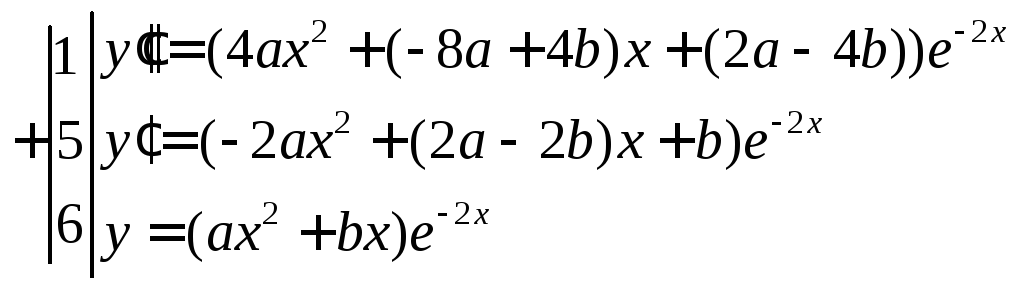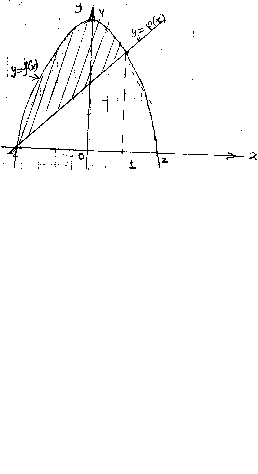
Решение

№ п/п

Алгоритм

Конкретное соответствие задания

предложенному алгоритму

1

Представить правую часть уравнения в виде

2

«Разделить» переменные и записать уравнение в виде

3

Проинтегрировать обе части полученного уравнения

;

.

Итак: , удобно взять произвольную постоянную в виде.

Окончательно:

или – общий интеграл уравнения.

№

п/п

Новое понятие

Содержание

1

2

3

1

Асимптота к графику функции y = f(x)

прямая Lтакая, что расстояниеdот точкиМна кривой до данной прямойLстремится к нулю при неограниченном удалении точкиМот начала координат

2

Бесконечно большая при

функция , для которой

3

Бесконечно малая при

функция , для которой

4

Вертикальная асимптота к графику функции y = f(x)

прямая х=а, если

5

Геометрический смысл дифференциала

приращение ординаты касательной

6

Геометрический смысл определенного интеграла

площадь S криволинейной трапеции, ограниченной непрерывной кривой y=f(x),, прямымих=а,х=bи осью0Х:

7

Геометрический смысл производной

тангенс угла наклона касательной в точке , где- угол наклона касательной

8

Глобальный максимум (минимум) функции

наибольшее (наименьшее) значение функции на всей области определения

9

Дифференциал функции

у = f (x) в точке х₀

главная часть приращения функции, линейная относительно ,, если х – независимая переменная, то

10

Дифференциальное уравнение

уравнение, связывающее независимую переменную х, искомую функциюу=у(х) и ее производные:

11

Достаточное условие возрастания функции у = f(x) на (а, b)

для всех

12

Достаточное условие интегрируемости функции f(x) на интервале

непрерывность функции на данном интервале

13

Достаточное условие точки перегиба функции y = f(x)

если в точке х₀ислева и справа от точких₀имеет разные знаки, тох₀– точка перегиба функции

14

Достаточное условие убывания функции у = f(x) на (а, b)

для всех

15

Достаточный признак экстремума функции

если при переходе через стационарную точку х₀слева направо по оси0Xпроизводная функции меняет знак, тох₀является точкой экстремума

16

Задача Коши для дифференциального уравнения

найти решение у=у(х) уравнения, удовлетворяющее начальным условиям, или

17

Интегральная кривая

график кривой у=у(х), являющейся решением дифференциального уравнения

1

2

3

18

Интегрирование функции f(x)

операция отыскания всех первообразных для функции f(x)

19

Левый предел функции f(x) в точке х₀

число , равное

20

Линейное дифференциальное уравнение первого порядка

уравнение вида , гдер(х) иq(x) – данные непрерывные функции

21

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

уравнение вида ,– постоянные

22

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

уравнение вида , где– постоянные

23

Наклонная асимптота к графику функции y = f(x)

прямая у=kх +bтакая, что

,

(k,b– конечные числа)

24

Необходимое условие точки перегиба

если х₀– точка перегиба дважды дифференцируемой функции, то

25

Необходимый признак экстремума дифференцируемой функции

если функция y=f(x) в точке х₀имеет экстремум и дифференцируема в этой точке, то

26

Общее решение дифференциального уравнения

функция у=у(х,с), зависящая от аргументахи произвольной постояннойс, удовлетворяющая условиям:

1) при любых значениях постоянной с функция у=у(х,с) является решением уравнения;

2) для любой точки , лежащей внутри областиD, существует единственное значение постояннойс=с₀такое, что

27

Определенный интеграл

такое число I, которое удовлетворяет условию: для любогосуществуеттакое, что при max

() и любом выборе точек,k=1,2,…n, выполняется неравенство

28

Первообразная для функции f(x)

функция F(x) такая, чтоили

29

Порядок дифференциального уравнения

высший из порядков производных, входящих в уравнение

30

Правый предел функции f(x) в точке х₀

число

31

Предел последовательности

такое число а, что для любого сколь угодно малого числанайдется такой номерN, что для всехn>Nверно неравенство

1

2

3

32

Предел функции у = f(x) на бесконечности при

такое число А, что для любогонайдется такое числоМ>0, что для всехвыполняется неравенствоили

33

Предел функции у = f(х) при стремлении х к х_о

такое число А, что для любогонайдется, что для всехх, удовлетворяющих условию, верно неравенство. Этот факт записывают так:

34

Производная n-го порядка функции y = f(x)

первая производная от (n–1)-й производной этой функции

35

Производная функции в точке х₀

предел отношения приращения функции к приращению аргументапри стремлениик нулю:

36

Решение дифференциального уравнения

функция у=у(х), которая при подстановке в уравнение обращает его в верное равенство (тождество)

37

Стационарные точки функции y = f(x)

точки, в которых производная дифференцируемой функции равна нулю

38

Точка локального максимума (max) функции у = f(x)

точка х₀такая, чтодля всеххиз окрестности точких₀, принадлежащей ее области определения

39

Точка локального минимума (min) функции у = f(x)

точка такая, чтодля всеххиз окрестности точких₁, принадлежащей ее области определения

40

Точка перегиба функции y = f (x)

точка х₀такая, что точкана графике функции отделяет выпуклую часть графика от вогнутой

41

Точка разрыва функции у = f(x)

точка х₀, в которой нарушается условие непрерывности функции

42

Точки экстремума функции

точки максимума и минимума функции, лежащие внутри интервала определения функции

43

Уравнение с разделяющимися переменными

дифференциальное уравнение вида

44

Формула Ньютона-Лейбница

формула вычисления определенного интеграла: , гдеF(x) – любая первообразная функцииf(x)

45

Формула интегрирования по частям

46

Формула интегрирования по частям в определенном интеграле

47

Формула Тейлора функции y = f(x) в окрестности точки х₀

формула, представляющая дифференцируемую функцию f(x) в окрестности точких₀в виде многочлена:

48

Функция f(x) выпукла на интервале (а, b)

если касательная к графику функции в каждой точке M0лежит не выше графика функции

1

2

3

49

Функция у = f(x) монотонна на (а, b)

если она возрастает или убывает на интервале (а,b)

50

Функция у = f(x), непрерывная в точке х₀

функция, для которой выполняется условие , или

51

Функция у = f(x), убывающая на интервале (а, b)

если большему значению аргумента из (а, b) соответствует меньшее значение функции, т.е. для верно неравенство

52

Функция у= f(x), возрастающая на интервале (а, b)

если большему значению аргумента из (а,b) соответствует большее значение функции, т.е. дляверно неравенство

53

Частное решение дифференциального уравнения

решение уравнения, полученное из общего у=у(х,с) при конкретном значении постояннойс=с₀
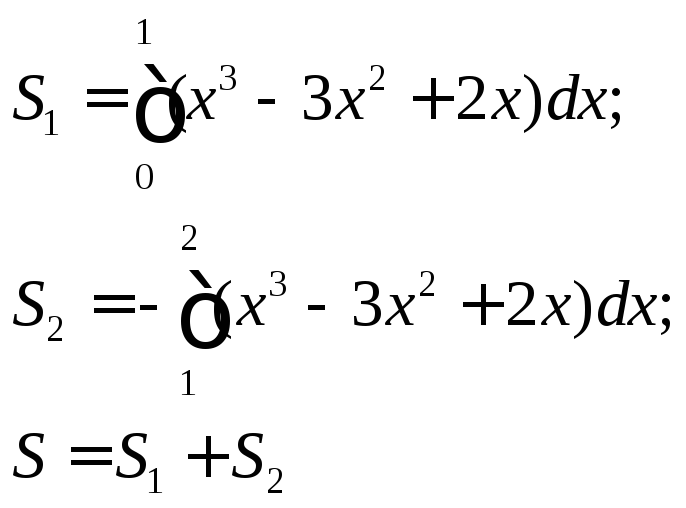
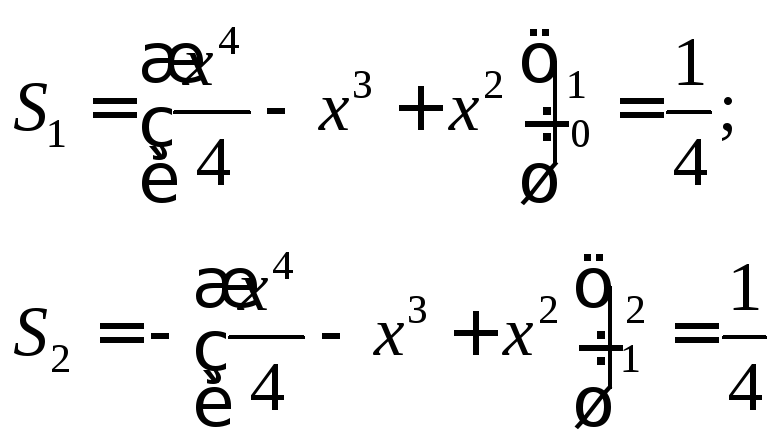
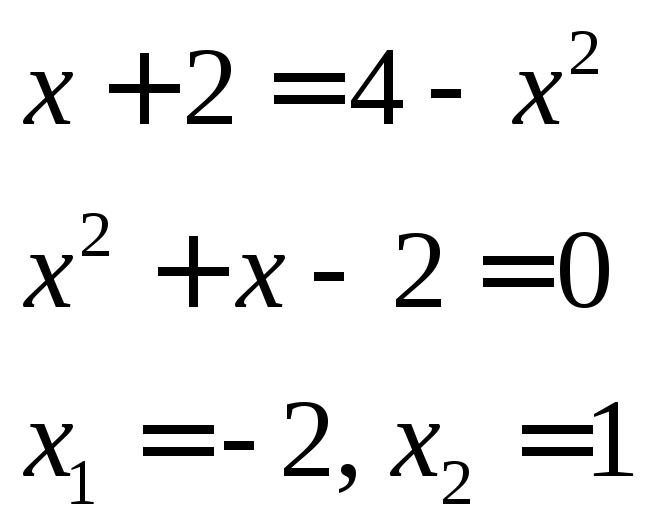
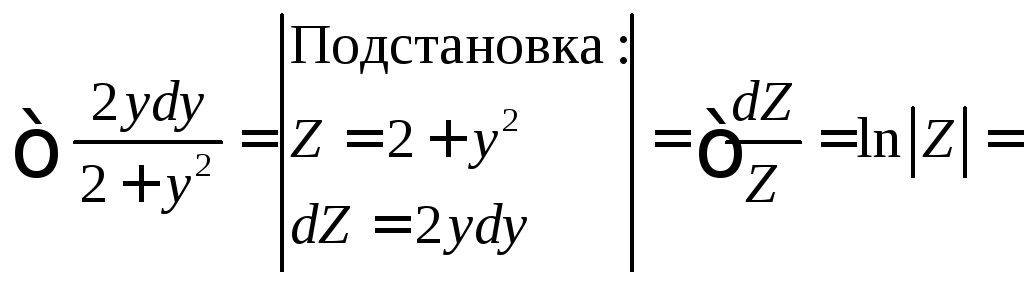
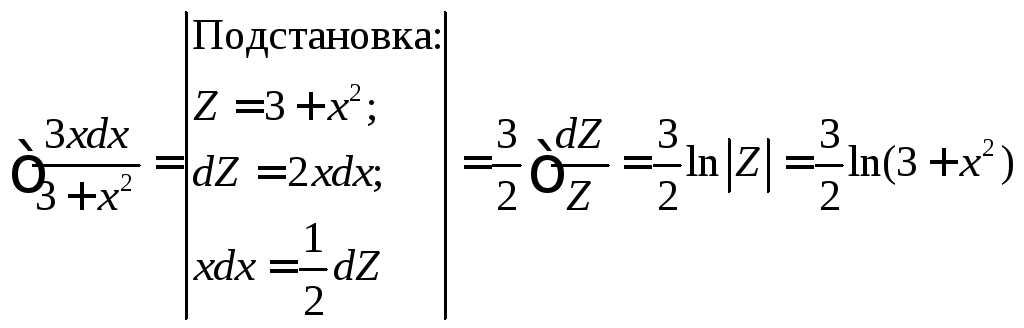