
4 раздел АиГ-элем линалгебры
.docx$$$94 D
Оz
осінен қиылған
 жазықтықтың
қимасын анықтаңдар:
жазықтықтың
қимасын анықтаңдар:
A) –2
B) 2
C) – 0,5
D) 0,5
E) 1
$$$95 D
 векторының
векторының
 жазықтығымен жасайтын бұрышты табыңдар:
жазықтығымен жасайтын бұрышты табыңдар:
A) 0
B)
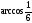
C)

D)

E) 60°
$$$96 B
Координата
басынан және
 мен
мен
 нүктелерінен өтетін жазықтықтың теңдеуін
жазыңдар:
нүктелерінен өтетін жазықтықтың теңдеуін
жазыңдар:
A)

B)

C)

D)

E)

$$$97C
 ,
,
 нүктелері
үшін, АВ кесіндісінің ортасының
координаттарын жазыңдар:
нүктелері
үшін, АВ кесіндісінің ортасының
координаттарын жазыңдар:
A)

B)

C)

D)

E)

$$$98 E
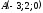 және
және
 нүктелері берілген, АВ кесіндісін
нүктелері берілген, АВ кесіндісін
 қатынасымен бөлетін С нүктесінің
абциссасын анықтаңдар:
қатынасымен бөлетін С нүктесінің
абциссасын анықтаңдар:
A) 0
B) 2
C)

D)
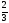
E)

$$$99 C
Жазықтықтағы түзудің канондық түрінің дұрыс формуласын анықтаңыз:
A)

B)

C)

D)

E)

$$$100 B
 және
және
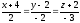 түзулерінің арақашықтықтарын жазыңдар:
түзулерінің арақашықтықтарын жазыңдар:
A) 5
B) 6
C) 7
D) 8
E) –3
@@@ Векторлық алгебра
$$$ 1 A
 және
және
 нүктелері
берілген.
нүктелері
берілген.
 -ны
табыңдар.
-ны
табыңдар.
A) ;
;
B)5;
C) ;
;
D) ;
;
E)3.
$$$ 2D
 және
және
 нүктелері
берілген.
нүктелері
берілген.
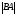 -ны
табыңдар.
-ны
табыңдар.
A)5;
B)7;
C) ;
;
D) ;
;
E) .
.
$$$ 3D
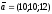 және
және
 векторлары
берілсін.
векторлары
берілсін.
 -ны
табыңдар.
-ны
табыңдар.
A) ;
;
B) ;
;
C) ;
;
D) ;
;
E) .
.
$$$ 4 B
 (4;2;-7)және
(4;2;-7)және
 векторлары
берілсін.
векторлары
берілсін.
 -ны
табыңдар.
-ны
табыңдар.
A) ;
;
B) ;
;
C) ;
;
D) ;
;
E)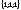 .
.
$$$ 5 C
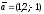 және
және
 векторлары
берілген.
векторлары
берілген.
 -ны
табыңдар.
-ны
табыңдар.
A)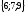 ;
;
B) ;
;
C)
 ;
;
D)
 ;
;
E)
 .
.
$$$ 6 A
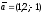 және
және
 векторлары
берілген.
2а+3b-ны
табыңдар.
векторлары
берілген.
2а+3b-ны
табыңдар.
A)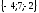 ;
;
B)
 ;
;
C)
 ;
;
D)
 ;
;
E)
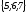 .
.
$$$ 7D
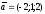 және
векторы
берілген.
және
векторы
берілген.
 векторының
бірлік векторын табыңдар.
векторының
бірлік векторын табыңдар.
A) ;
;
B)
 ;
;
C)
 ;
;
D)
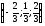 ;
;
E) .
.
$$$ 8 B
 және
векторы
берілген.
және
векторы
берілген.
 векторының
бірлік векторын табыңдар.
векторының
бірлік векторын табыңдар.
A) ;
;
B)
 ;
;
C)
 ;
;
D)
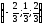 ;
;
E)
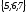 .
.
$$$ 9 A
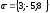 және
және
 векторы берілген
векторы берілген
 -ны
табыңдар.
-ны
табыңдар.
А) 6;
В) 9;
С)8;
D) 10;
Е) 5;
$$$ 10 C
 және
және
 векторы берілген
векторы берілген
 -ны
табыңдар.
-ны
табыңдар.
А) 5;
В)
 ;
;
С)
 ;
;
D)
 ;
;
Е)
 .
.
$$$ 11D
 және
және
 векторы берілген
векторы берілген
 -ны табыңдар.
-ны табыңдар.
А) 20;
В) 3;
С) 5;
D) 0;
Е) 6.
$$$ 12 D
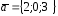 және
және
 векторы берілген
векторы берілген
 -ны табыңдар
-ны табыңдар
А) -10;
В) 2;
С) 12;
D) 10;
Е) -12.
$$$ 13 А
 және
және
 векторларының
арасындағы бұрышы
векторларының
арасындағы бұрышы
 -ны
табыңдар.
-ны
табыңдар.
А)

В) 6
С)

D)

E)

$$$ 14 E
 және
және
 векторларының
арасындағы бұрыштың
косинусын табыңдар.
векторларының
арасындағы бұрыштың
косинусын табыңдар.
А) 3
В)

С) 0
D) 5
Е)

$$$ 15 E
 және
және
 векторларының
арасындағы бұрыштың
косинусын табыңдар.
векторларының
арасындағы бұрыштың
косинусын табыңдар.
А) 3
В)

С) 0
D) 5
Е)

$$$ 16 B
 және
және
 векторларының
арасындағы бұрышты
табыңдар,
егер
векторларының
арасындағы бұрышты
табыңдар,
егер
 болса.
болса.
А) 0;
В)

С)

D)

Е)

$$$ 17 B
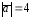 және
және
 векторларының
арасындағы бұрышы
векторларының
арасындағы бұрышы
 -ны
табыңдар.
-ны
табыңдар.
А) 0
В) 10
С) 7
Д) 15
Е) 18
$$$ 18 C
 және
және
 векторларының
арасындағы бұрыш
векторларының
арасындағы бұрыш
 -ны
табыңдар
-ны
табыңдар
А) 0
В) 12
С) 6
D)

Е)

$$$ 19 A
Егер
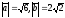 және арасындағы бұрышы 300
болсын.
және арасындағы бұрышы 300
болсын.
 және
және
 векторларының скаляр көбейтіндісін
табыңдар.
векторларының скаляр көбейтіндісін
табыңдар.
А) 6;
В)
8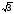 ;
;
С) 3;
D) 12;
E)
6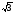 .
.
$$$ 20 B
А(2;0;1)
нүктесі арқылы өтетін және
 жазықтығына параллел болатын жазықтықтың
теңдеуін табыңдар.
жазықтығына параллел болатын жазықтықтың
теңдеуін табыңдар.
А)
 ;
;
В)
 ;
;
С)
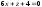 ;
;
D)
 ;
;
E)
 .
.
$$$ 21 D
Төмендегі жазықтықтықтардың қай қосағы параллел жазықтықтықтарды анықтайды.
А)
4 ;
;
 ;
;
В)
 ;
;
 ;
;
С)
 ;
;

D)
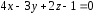 ;
;
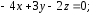
E)
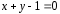 ;
;

$$$22 D
 векторы
векторы
 жазықтығымен қандай бұрыш жасайды.
жазықтығымен қандай бұрыш жасайды.
А) 0;
В)
 ;
;
С)
 ;
;
D)
 ;
;
E) 600.
$$$ 23 A
А(3;-2;1)
нүктесі арқылы өтетін,
 векторына параллель түзудің дағдылы
теңдеуін жазыңдар.
векторына параллель түзудің дағдылы
теңдеуін жазыңдар.
А)

В)
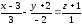 ;
;
С)
 ;
;
D)
 ;
;
E) Көрсетілгендерден басқа жауап.
$$$ 24 B
 түзуінің
түзуінің
 жазықтығымен қиылысу нүктесін табыңдар
жазықтығымен қиылысу нүктесін табыңдар
А) (2;-1;-3);
В) (-2;1;3);
С) Түзу жазықтықта жатады
D) Түзу жазықтықпен қиылысады.
E) (6;6;0).
$$$ 25 D
у=7x-2,
y=x-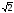 түзулерінің аравсындағы бұрышты тап
түзулерінің аравсындағы бұрышты тап
А) – arctg4,5
В) arctg6
С)
arccos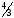
D)
arctg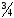
E) 600
$$$ 26 D
3x+7y+8=0 түзуінің бағыттаушы векторының координаталарын тап
А) {7; 3}
В) {-7;-3}
С) {-3;-7}
D) {-7;3}
E) {7; -8}
$$$ 27 C
М(2; 3;-1) нүктесі арқылы өтіп n={0;-3; 4} веторына перпендикуляр жазықтықтың теңдеуін жаз.
A) –3x-4z+3=0
D) 3x+3y-4z-13=0
C) 3x-4z-13=0
D) 2x+3y-z-13=0
E) –3x+4z-13=0.
$$$ 28 A
 және
және
 векторлары
берілсін.
векторлары
берілсін.
 -ны
табыңдар.
-ны
табыңдар.
A) ;
;
B) ;
;
C) ;
;
D)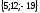 ;
;
E) .
.
$$$ 29 C
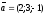 және
және
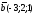 векторлары
берілген.2а+5b-ны
табыңдар.
векторлары
берілген.2а+5b-ны
табыңдар.
A) ;
;
B)
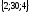 ;
;
C)
 ;
;
D)
 ;
;
E)
 .
.
$$$ 30 D
 және
және
 векторы
берілген
ab
-ны
табыңдар.
векторы
берілген
ab
-ны
табыңдар.
А) 6;
В) 9;
С)8;
D) -40;
Е) 5;
$$$ 31 C
 және
және
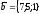 векторларының
арасындағы бұрыштың косинусын табыңдар.
векторларының
арасындағы бұрыштың косинусын табыңдар.
А) 3
В)

С) 0
D) 5
Е)

$$$ 32А
а=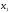 i+
i+ j+
j+ k
және b=
k
және b= i+
i+ j+
j+ k
векторлары берілсін. Векторлардың
қосындысы неге тең:
k
векторлары берілсін. Векторлардың
қосындысы неге тең:
А.a±b={ ;
; ;
; }
}
B.а·в=|а|·|в|·cos(а^в)
C. a=
a= (
( i+
i+ j+
j+ k)=
k)=

 i+
i+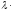
 j+
j+
 k=
k=
D.cos(а^в)=
E. =
= =
=
$$$ 33 B
а= i+
i+ j+
j+ k
және b=
k
және b= i+
i+ j+
j+ k
векторлары берілсін. Векторлардың
скаляр көбейтіндісі неге тең:
k
векторлары берілсін. Векторлардың
скаляр көбейтіндісі неге тең:
A.a±b={ ;
;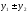 ;
; }
}
B.а·в=|а|·|в|·cos(а^в)
C.
 a=
a= (
( i+
i+ j+
j+ k)=
k)=

 i+
i+
 j+
j+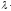
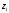 k=
k=
D.
cos(а^в)=
E.
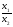 =
= =
=
$$$ 34 C
а= i+
i+ j+
j+ k
векторы берілсін. Вектордың скалярға
көбейтіндісі неге тең:
k
векторы берілсін. Вектордың скалярға
көбейтіндісі неге тең:
A.a±b={ ;
; ;
; }
}
B. а·в=|а|·|в|·cos(а^в)
C.
 a=
a=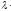 (
( i+
i+ j+
j+ k)=
k)=

 i+
i+
 j+
j+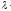
 k=
k=
D.
cos(а^в)=
E.
 =
= =
=
$$$ 35D
а= i+
i+ j+
j+ k
және b=
k
және b= i+
i+ j+
j+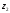 k
векторлары берілсін. Векторлардың
арасындағы бұрыш неге тең:
k
векторлары берілсін. Векторлардың
арасындағы бұрыш неге тең:
A.a±b={ ;
; ;
;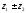 }
}
B. а·в=|а|·|в|·cos(а^в)
C.
 a=
a= (
( i+
i+ j+
j+ k)=
k)=

 i+
i+
 j+
j+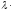
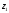 k=
k=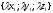
D.
cos(а^в)=
E.
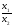 =
= =
=
$$$ 36 E
а=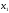 i+
i+ j+
j+ k
және b=
k
және b= i+
i+ j+
j+ k
векторлары берілсін. Векторлардың
коллениарлық белгісін көрсет:
k
векторлары берілсін. Векторлардың
коллениарлық белгісін көрсет:
A.a±b={ ;
; ;
; }
}
B. а·в=|а|·|в|·cos(а^в)
C.
a= (
( i+
i+ j+
j+ k)=
k)=

 i+
i+
 j+
j+
 k=
k=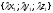
D.
cos(а^в)=
E.
 =
= =
=
$$$ 37 А
Вектор дегеніміз не?
A. бағытталған кесінді
B. тік бұрышты координаталар жүйесі
C. екі нүктенің ара қашықтығы
D.кесіндінің ұзындығы
E.кесінді
$$$38 С
Вектордың модулі дегеніміз не?
A. бағытталған кесінді
B. тік бұрышты координаталар жүйесі
C. вектордың ұзындығы
D. екі нүктенің ара қашықтығы
E.кесінді
$$$39 D
Қандай векторлар өзара коллинеар деп аталады?
A.бағыттас векторлар
B.модульдері тең векторлар
C.өзара тең векторлар
D.бір түзудің бойында немесе параллель түзулердің бойында жататын векторлар
E.бағыттары қарама-қарсы векторлар
$$$40 D
Қандай векторлар өзара тең деп аталады?
A.бағыттас болса
B.модульдері тең болса
C.өзара тең векторлар
D.коллинеар, ұзындықтары бірдей және бағыттас болса
E.бағыттары қарама-қарсы болса
$$$41 D
Қай тұжырым тура
A. жазықтықтағы кез келген a,b екі векторы өзара тәуелсіз
B. жазықтықтағы кез келген a,b,c үш векторы өзара тәуелсіз
C. жазықтықтағы кез келген a,b екі векторы өзара тәуелді
D.жазықтықтағы кез келген a,b,c үш векторы өзара тәуелді
E. жазықтықтағы кез келген векторлар өзара тәуелді
$$$42 D
Қай тұжырым тура
A. a,b екі векторы жазықтықта өзара тәуелсіз болуы үшін, олардың қарама-қарсы таңбалы болуы қажетті және жеткілікті
B. a,b екі векторы жазықтықта өзара тәуелсіз болуы үшін, олардың өзара тең болуы қажетті және жеткілікті
C. a,b екі векторы жазықтықта өзара тәуелсіз болуы үшін, олардың өзара компланар болуы қажетті және жеткілікті
D. a,b екі векторы жазықтықта өзара тәуелсіз болуы үшін, олардың өзара компланар болмауы қажетті және жеткілікті
E. a,b екі векторы жазықтықта өзара тәуелсіз болуы үшін, олардың өзара компланар болмауы қажетті
$$$43 D
Қай тұжырым тура
A. жазықтықтағы кез келген a,b екі векторы өзара тәуелсіз
B. кеңістіктегі кез келген a,b,c үш векторы өзара тәуелсіз
C. кеңістікте кез келген a,b екі векторы өзара тәуелді
D.кеңістіктегі кез келген a,b,c,d төрт векторы өзара тәуелді
E. жазықтықтағы кез келген векторлар өзара тәуелді
$$$44 А
Жазықтықтағы базис дегеніміз не?
A.жазықтықтағы кезкелген екі сызықтық тәуелсіз вектор
B. жазықтықтағы кезкелген екі сызықтық тәуелді вектор
C. кеңістіктегі кезкелген екі сызықтық тәуелді вектор
D. кеңістіктегі кезкелген екі сызықтық тәуелсіз вектор
E. жазықтықтағы кезкелген сызықтық тәуелді векторлар
$$$45 Е
Кеңістіктегі базис дегеніміз не?
A.кеңістіктегі кезкелген векторлар
B. жазықтықтағы кезкелген үш сызықтық тәуелді вектор
C. жазықтықтағы кезкелген үш сызықтық тәуелсіз вектор
D. кеңістіктегі кезкелген үш сызықтық тәуелді вектор
E. кеңістіктегі кезкелген үш сызықтық тәуелсіз вектор
$$$46 Е
 векторының
координаттарын анықта,
егер
А(2;-1;3) и В (4;-2;3) болса:
векторының
координаттарын анықта,
егер
А(2;-1;3) и В (4;-2;3) болса:
А) {6;1;6}
В) {3;4;9}
С) {1;1;1}
D) {0;6;4}
Е) {2;-1;0}
$$$47 С
А(3;-1;2)
және В
(2;3;4) ,
 -
ны тап:
-
ны тап:
А) {5;2;6}
В) {1;-4;2}
С) {1;-4;-2}
D) {0;6;4}
Е) {0;20;10}
$$$48 А
А(1;3;2)
және В
(5;8;-1) ,
 -
ны тап:
-
ны тап:
А) {4;5;-3}
В) {6;11;1}
С) {-4;-5;3}
D) {1;3;4}
Е) {1;0;0}
$$$49 А
А
(1;2;3) және
В
(4;5;6)
берілген.
 -ны
тап:
-ны
тап:
А)
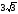
В) 5
С)

D)
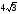
Е) 3
$$$ 50 D
А
(4;2;1) және
В (3;5;4)
берілген.
 - ны
тап:
- ны
тап:
А) 5
В) 7
С)

D)
Е)
$$$ 51А
 және
және
 .
.
 -ны
тап:
-ны
тап:
А) {5;12;19}
В) {1;1;0}
С) {2;1;2}
D) {5;12;-19}
Е) {0;1;0}
$$$ 52 В
 -ны
тап ,
егер
-ны
тап ,
егер
 және
және
 :
:
А) {3;7;0}
В) {7;0;-14}
С) {2;2;4}
D) {-7;1;-4}
Е) {1;1;1}
$$$ 53 С
 ,
,
 берілген,
берілген,
 -ны
тап
:
-ны
тап
:
А) {6;7;9}
В) {-1;2;0}
С) {-3;4;-1}
D) {5;6;7}
Е){20;3;4}
$$$ 54 Е
 векторының
ұзындығын
тап:
векторының
ұзындығын
тап:
А) 9
В) 13
С) 4
D) -2
Е) 3
$$$ 55 А
 және
және
 берілген.
берілген.
 -ны
тап:
-ны
тап:
А) {-4;7;-2}
В) {2;30;4}
С) {-1;2;0}
D) {6;7;9}
Е) {5;6;7}
$$$ 56 D
 векторының
бірлік векторын тап:
векторының
бірлік векторын тап:
А) {1;0;0}
В) {0;1;0}
С) {1;1;1}
D) {

 }
}
Е) {

 }
}
$$$57 А
 және
және
 векторлары
берілген.
векторлары
берілген.
 -ны
тап:
-ны
тап:
А) 6
В) 9
С) 8
D) 10
Е) 5
$$$58 Е
 және
және
 берілген,
берілген,
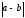 -ны
тап:
-ны
тап:
А 5
В

С

D

Е 14
$$$59 В
 ,
,
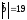 ,
,
 болса, онда
болса, онда
 -ны
тап:
-ны
тап:
А) 20
В) 22
С) 6
D) 12
Е) 16
$$$60С
 ,
,
 ,
,
 болса, онда
болса, онда
 -ны
тап:
-ны
тап:
А) 18
В) 24
С) 20
D) 26
Е) 16
$$$61 А
 ,
,
 векторлары α мен β ның қандай мәнінде
коллинеарлы болаDы?
векторлары α мен β ның қандай мәнінде
коллинеарлы болаDы?
А) α=3/4; β=-8/3
В) α=1/2; β=2/3
С) α=2; β=1/3
D) α=1; β=-2
Е) α=2/3; β=1/2
$$$62 D
 ,
,
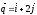 векторлары берілген,
векторлары берілген,

 және
және
 базистік векторы бойынша жіктелуін
тап:
базистік векторы бойынша жіктелуін
тап:
А)

В)
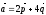
С)

D)

Е)

$$$ 63А
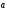 және
және
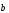 векторларының
арасындағы бұрыш
векторларының
арасындағы бұрыш
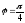 ,
ал
ұзындықтары
,
ал
ұзындықтары
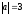 ,
,
 болса,
онда
болса,
онда
 скалярлық
көбейтіндісін тап:
скалярлық
көбейтіндісін тап:
А

В 6
С

D

Е
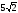
$$$64 D
 ,
,

 берілген,
берілген,
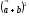 -ны
тап:
-ны
тап:
А)40
В) 35
С) 45
D) 37
Е) 39
$$$ 65 D
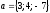 ,
,
 векторларының скаляр көбейтіндісін
тап:
векторларының скаляр көбейтіндісін
тап:
A) 20
B) 3
C) 5
D) 0
E) 6
$$$ 66 D
 ,
,
 берілген.
берілген.
 -ны
тап
-ны
тап
А) -10
В) 2
С) 12
D) 10
Е) –12
$$$ 67А
 ,
,
 берілген.
берілген.
 векторлардың
скалярлық көбейтіндісін тап:
векторлардың
скалярлық көбейтіндісін тап:
A) -13
