Тетрадь 2 (аналитическая геометрия)

Учимося розв’язувати типові задачі

1.19. Знайдіть рівняння прямої, яка проходить через точку M (1; 2) , паралельно до прямої 3x 2 y 5 0.

Хід розв’язання.

14

І спосіб (за допомогою рівняння прямої з кутовим коефіцієнтом).

Крок 1. Запишіть рівняння прямої 3x 2 y 5 0 у вигляді рівняння прямої з кутовим коефіцієнтом та запишіть її кутовий коефіцієнт k1 .

y k1

Рівняння прямої з кутовим коефіцієнтом має вигляд y k x b , де k кутовий коефіцієнт, b відрізок, що відсікається прямою на осі ординат.

Крок 2. Знайдіть кутовий коефіцієнт k2 прямої, паралельної до прямої y 32 x 52 .

k2

Якщо прямі l1 і l2 , задані рівняннями з кутовими коефіцієнтами y k1 x b1 і y k2 x b2 паралельні, то k1 k2 .

Рівняння прямої, що проходить через задану точку M0 (x0 , y0 ) із заданим кутовим коефіцієнтом k має вигляд y y0 k(x x0 ) .

Крок 4. Розкрийте дужки та запишіть одержане рівняння в загальному вигляді.

Загальне рівняння прямої на площині має вигляд A x B y C 0

15

Відповідь: 3x 2 y 5 0.

ІІ спосіб.

Крок 1. Знайдіть координати нормального вектора n прямої

3x 2 y 5 0.

n ...

Скористайтесь означенням загального рівняння прямої на площині: загальне рівняння прямої на площині має вигляд Ax By C 0 , де A і B – координати вектора

n , перпендикулярного до прямої.

Крок 2. Запишіть рівняння прямої, яка проходить через точку M (1; 2) , з нормальним вектором n 3, 2 .

Через те, що шукана пряма паралельна до прямої 3x 2y 5 0 , то вектор n , перпендикулярний до цієї прямої, також перпендикулярний і до шуканої прямої (рис.1.4.)

Рис. 1.4. Схематичне зображення інформаційної підтримки

Рівняння A x x0 B y y0 0 називають рівнянням прямої, яка проходить через точку M0 (x0 , y0 ) перпендикулярно до вектора n A, B .

Крок 3. Розкрийте дужки та запишіть одержане рівняння в загальному вигляді.

16

Загальне рівняння прямої на площині має вигляд A x B y C 0

Відповідь: 3x 2 y 5 0.

1.20. Знайдіть рівняння прямої, яка проходить через точку M ( 3;1) , перпендикулярно до прямої 4x 3y 2 0 .

Хід розв’язання.

І спосіб (за допомогою рівняння прямої з кутовим коефіцієнтом).

Крок 1. Запишіть рівняння прямої 4x 3y 2 0 у вигляді рівняння прямої з кутовим коефіцієнтом та запишіть її кутовий коефіцієнт k1 .

Крок 3. Запишіть рівняння прямої, що проходить через точку

M ( 3;1) з кутовим коефіцієнтом k2 34 .

17

Рівняння прямої, що проходить через задану точку M0 (x0 , y0 ) із заданим кутовим коефіцієнтом k має вигляд y y0 k(x x0 ) .

Крок 4. Розкрийте дужки та запишіть одержане рівняння у загальному вигляді.

Загальне рівняння прямої на площині має вигляд A x B y C 0

Відповідь: 3x 4 y 5 0

ІІ спосіб.

Хід розв’язання.

Крок 1. Знайдіть координати нормального вектора n прямої

4x 3y 2 0 .

n ...

Скористайтесь означенням загального рівняння прямої на площині: загальне рівняння прямої на площині має вигляд Ax By C 0 , де A і B – координати вектора

n , перпендикулярного до прямої.

Крок 2. Запишіть рівняння прямої, яка проходить через точку M ( 3;1) з напрямним вектором a n 4, 3 , тобто канонічне рівняння

прямої.

Так як шукана пряма перпендикулярна до прямої 4x 3y 2 0 , то вектор n , перпендикулярний до цієї прямої, є напрямним до шуканої прямої (рис.1.5.)

18

Рис.1.5. Схематичне зображення інформаційної підтримки

проходить через точку M0 (x0 , y0 ) з напрямним вектором а l, m .

Крок 3. Застосувавши правило пропорції, запишіть одержане рівняння у загальному вигляді.

Загальне рівняння прямої на площині має вигляд A x B y C 0

Відповідь: 3x 4 y 5 0.

1.21. Знайдіть рівняння прямої, яка проходить через точку A(2,4) та точку перетину прямих 2x y 4 0 і x y 2 0 .

Хід розв’язання.

Крок 1. Знайдіть координати точки B перетину прямих 2x y 4 0 і x y 2 0 . Для цього складіть та розв’яжіть систему лінійних рівнянь.

Для розв’язування застосуйте будь-який відомий вам метод, наприклад метод підстановки.

19

x 6

B(6, 8)

y 8

Якщо дві прямі перетинаються, то вони мають єдину спільну точку, координати якої можна одержати як розв’язок системи, що поєднує лінійні рівняння цих прямих.

Крок 2. Запишіть рівняння прямої, що проходить через дві задані точки A(2,4) і B(6, 8) .

Крок 3. Застосувавши правило пропорції, запишіть одержане рівняння в загальному вигляді.

Загальне рівняння прямої на площині має вигляд A x B y C 0

Відповідь: 3x y 9 0.

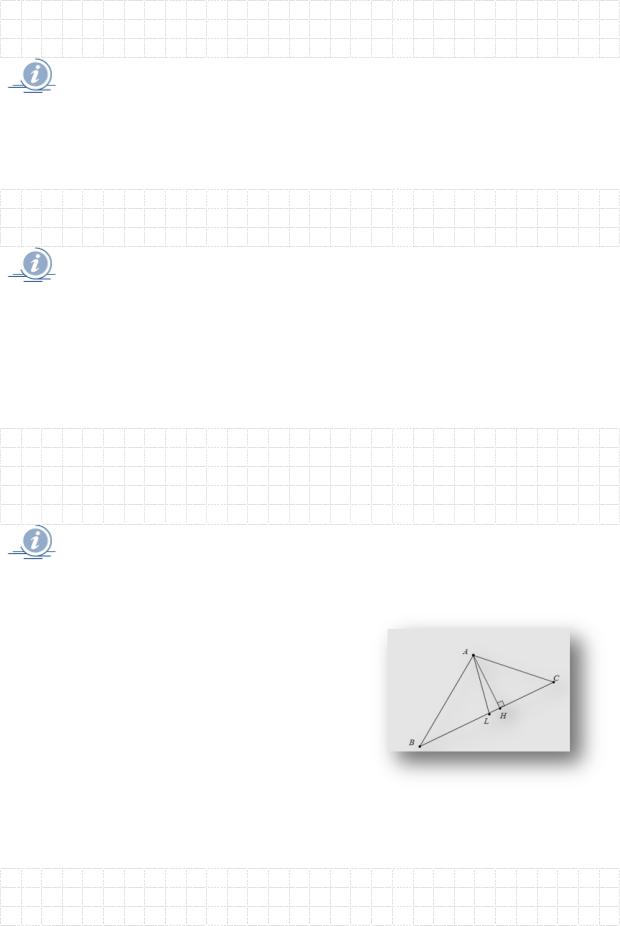
1.22.Знайдіть рівняння медіани AL

івисоти AH трикутника ABC (рис.1.6.),

якщо відомі координати вершин трикутника A(2,4), B( 4,1),C(0,3) .

Хід розв’язання.

Рис.1.6. Зображення трикутника

Отже, отримали L( 2,2) .

Крок 2. Знайдіть рівняння медіани AL . Застосуйте рівняння прямої, яка проходить через дві відомі точки A(2,4) і L( 2,2) та запишіть його в

загальному вигляді.

Загальне рівняння прямої на площині має вигляд A x B y C 0 .

Отже, отримали рівняння медіани AL : x 2y 6 0.

Крок 3. Знайдіть координати вектора BC .

BC

Крок 4. Знайдіть рівняння висоти AH . Скористайтесь тим, що вектор

BC , перпендикулярний до висоти AH , є нормальним вектором прямої AH . Застосуйте рівняння прямої, яка проходить через точку A(2,4) з нормальним

вектором n BC 4;2 .

21

Скористайтесь означенням загального рівняння прямої на площині: загальне рівняння прямої на площині має вигляд Ax By C 0 , де A і B – координати вектора

n , перпендикулярного до прямої.

Крок 2. Знайдіть скалярний добуток n1 n2 та модулі векторів n1 , n2 .

n1 n2 n1 n2

Скористайтесь формулою для обчислення скалярного добутку векторів на площині, які задано своїми координатами: якщо a ax ; ay , b bx ; by , то

a b ax bx ay by .

Скористайтесь формулою для знаходження модуля вектора a ax ; ay : a ax2 ay2 .

22