РОЗВ’ЯЗАННЯ ЗАВДАНЬ Частина – 1. Теорія множин. Математична логіка. Комбінаторний аналіз.

Завдання 1.

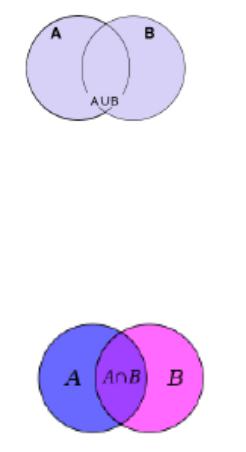
1. Об’єднанням множин A і B є множина, яка включає всі елементи A і всі елементи B, і більш нічого.

Позначається як « A B ».

Формально: х є елементом A B тоді і тільки тоді, коли х є елементом А або х є елементом В.

Графічне зображення:

2. Перетином двох множин A та B називається множина, яка складається з усіх елементів множини A, які одночасно належать і множині B та навпаки (всі елементи множини B які належать A) і тільки їх.

Позначаеться як « A B ».

Формально: A B {x | (x A) (x B)}.

Графічне зображення:

Якщо перетин двох множин A та B є порожнім, тобто не містить спільних елементів, то кажуть, що такі множини не перетинаються. Цей факт позначається як A B .

3. Різницею між B та А (порядок множин важливий), або відносним доповненням A до B, є множина з елементів B, які не належать A.

Позначається: B \ A Ac B .

Формально: B A {x | (x B) (x A)}.

Графічне зображення:

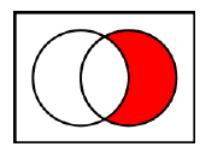
Отже, для A {1,4,6,9}, B {2,3,5,7,9}: A B {1,2,3,4,5,6,7,9}

A B {9} A \ B {1,4,6}

B \ A {2,3,5,7}.

Завдання 2.

Круги Ейлера - геометрична схема, за допомогою якої можна зобразити відносини між підмножинами, для наглядного представленія.

Винайдені Леонардом Ейлером. Використовується в математиці, логіці,

менеджменті і інших прикладних напрямках.

Діаграма Ейлера-Венна - наочний засіб для роботи зі множинами. На цих діаграмах зображуються всі можливі варіанти перетину множин.

Кількість перетинів (областей) n визначається за формулою: n 2N , де N - кількість множин.

Таким чином, якщо в задачі використовується дві множини, то n 22 4

, якщо три множини, то n 23 8 , якщо чотири множини, то n 24 16 . Тому діаграми Ейлера-Венна використовуються в основному для двох або трьох

множин.

Безлічі зображуються у вигляді кіл (якщо використовується 2-3 множини)

і еліпсів (якщо використовується 4 множини), поміщених в прямокутник

(універсум).

Отже, для (A C) \ (C B) :

1. Спочатку визначимо частину (A C) :

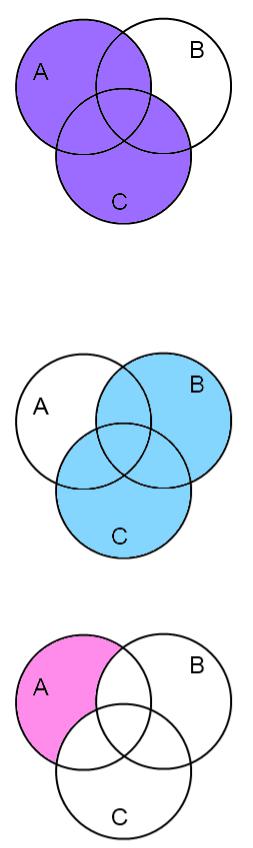
2.Визначимо (C B) :

3. позначимо різницю (A C) \ (C B):

Завдання 3.

Кількість усіх сполучень без повторень з n елементів по r позначають як

розміщення без повторень з n елементів, коли в розміщення входять всі елементи. Перестановки з n елементів також називають n-перестановками.

Окремі n-перестановки різняться лише порядком елементів. Кількість таких перестановок позначають як Pn . Формулу для Pn одержують із формули для кількості розміщень без повторень: Pn Ann n! (5.1)

Отже, «ковдра»: n 6, P6 6! 720.

2.Перестановка з повтореннями – це перестановки n елементів за

умови, що не всі елементи різні. Кількість таких перестановок позначають як Рn(n1, n2,…,nk). Щоб знайти явний вираз для Рn(n1, n2,…,nk), візьмемо окрему перестановку та замінимо в ній усі однакові елементи різними. Тоді