Лекція №7. Формула Остроградського – Ліувілля. Лінійні однорідні рівняння з постійними коефіцієнтами

1. Формула Остроградського – Ліувілля та її застосування для розв’язку рівняння другого порядка.

Теорема (Остроградського – Ліувілля). Нехай дано однорідне рівняння

y+p(x)y+…+p(x)y=0, де p…p–неперервні на [a;b] і (y,…,y)–фундаментальна система рішень, тоді справедлива формула W(х)=с, (с – довільна константа), або W(х)= W()_.

Доведення. Враховуючи властивості визначника і диференціювання, а також той факт, що y,…,yє рішення даного рівняння, отримаємо

.

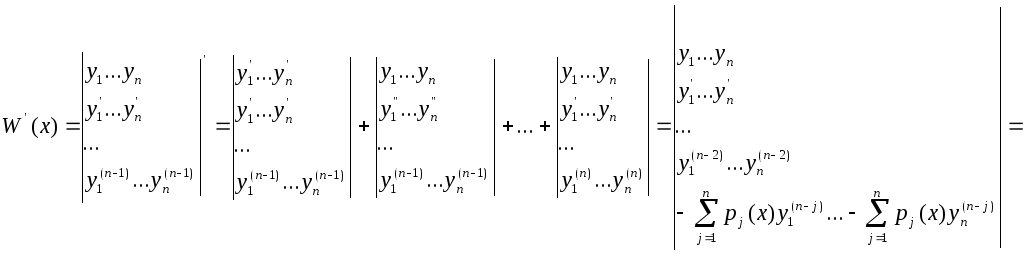
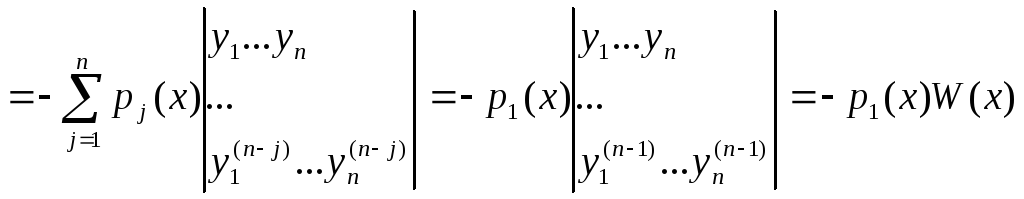Отже, визначник Вронского задовольняє наступне рівняння W′ = - p(x)W. Розв’язуючи яке будемо мати W(x) = с , або W(x) = W()с _.

Зауваження. Розглянемо y′′+p(x)y′+p(x)y=0 – рівняння другого порядку, тоді, якщо у - будь-який розв’язок рівняння, то можна знайти загальне рішення в такий спосіб. Нехай у - загальне рішення, розглянемо рівність

.

Отже, відносно у отримаємо рівняння першого порядку yy′- y′y=c_{, розв’язуючи яке знайдемо загальний розв’язок вихідного рівняння.}

Приклад. y′′+y′ - =0. За допомогою підстановки легко довести, щоy=x рішення рівняння. Відповідне рівняння для загального рішення даного рівняння має вид y -y′x= – лінійне рівняння першого порядку. Для його розв’язку знайдемо розв’язок рівнянняy′x=y або . Отжеy=cx. Загальний розв’язок рівняння шукаємо у виглядіy=c(x) x, де c(x) невідома функція. Підставляючи цей y у рівняння отримаємо

c′x²+c(x) x – c(x) x+=0, тобто c′=. Отже c(x) = dx і y= dx.

Зауваження. Аналогічно можна застосовувати формулу і у випадку рівняння n-го порядку коли відомі будь-які незалежні рішення рівняння, що буде приводити до зниження порядка рівняння на 1.

2. Лінійні однорідні рівняння з постійними коефіцієнтами.

Задача знаходження фундаментальної системи рішень, а отже й загального рішення, спрощується у випадку рівняння з постійними коефіцієнтами.

Означення. Рівняння виду y+ay+…+ay=0, де а,…,а– довільні константи, називається лінійним однорідним рівнянням з постійними коефіцієнтами.

Рішення рівняння шукають у вигляді у=. Підставляючиу= у рівняння отримаємо, що k задовольняє рівнянню kⁿ+ak+…+a=0.

Означення. Рівняння kⁿ+ak+…+a=0 називають характеристичним рівнянням для даного диференціального рівняння.

Існує декілька випадків відносно розв’язка характеристичного рівняння.

1. Характеристичне рівняння має n різних дійсних коренів . Розглянемо функціїу=,…, у= усі вони є рішеннями даного диференціального рівняння і лінійно незалежні, оскільки

.

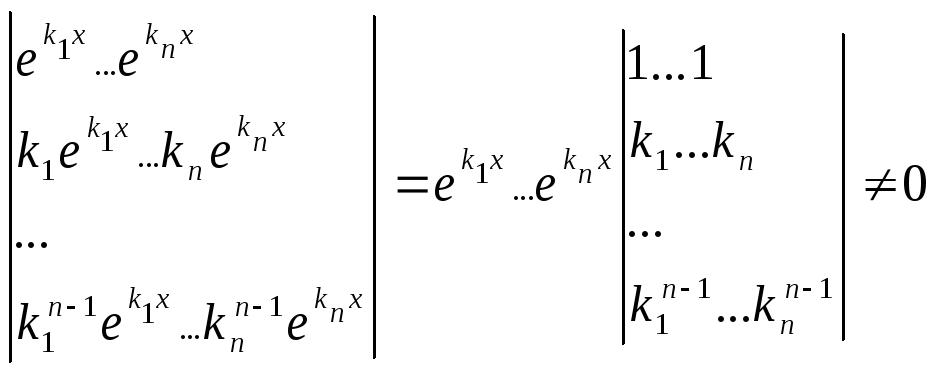Отже у=,…, у= - фундаментальна система рішень і у=с+…+с – загальне рішення лінійного однорідного диференціального рівняння з постійними коефіцієнтами.

2. Припустимо, що якийсь корінь ki дійсний, але має кратність p. Тоді – лінійно незалежна система функцій, які також являються рішеннями вихідного рівняння, що не важко перевірити підставляючи їх у рівняння, враховуючи кратністьki . Загальний розв’язок рівняння будується аналогічно 1 з урахуванням вище сказаного.

3. Припустимо, що характеристичне рівняння має комплексний корінь k=α+βi, тоді спряжене число k=α-βiтеж корінь характеристичного рівняння. Цім кореням відповідають дві функції , _{в фундаментальній системі розв’язків.}

Скористувавшись формулами Ейлера ці функції можна замінити на дійснозначні. Оскільки

= (cosβx+isinβx)_, = (cosβx-isinβx), то ,

, або у= cosβx, у=sinβx– рішення рівняння і лінійно незалежні. Загальний розв’язок будується аналогічно 1.

4. Якщо комплексний корінь k=α+βiмає кратність p, спряжений корінь k=α-βiтеж має кратність p. Тоді аналогічно випадкам 2 і 3 цім кореням відповідає система лінійно незалежних рішень рівняння:

cosβx, xcosβx,…,cosβx, sinβx,xsinβx,…,sinβx_{, за допомогою яких і будується загальне рішення.}