04_Магнетизм

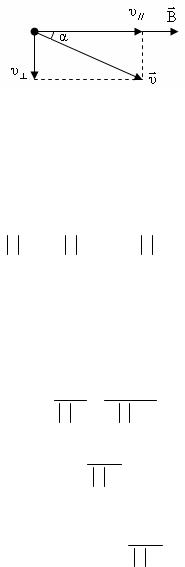
Разложим υr на составляющие υ// и υ :

υ// = υcosα,

υ= υsinα.

Запишем для магнитной силы:

F = q[(υr + υr// )×B]=

= q[υr ×Br]+ q[υr// ×Br]= q[υr ×Br], F = q υ B = q υsinαB = q υBsinα .

Частица одновременно участвует в двух движениях. Она равномерно и прямолинейно движется в направлении магнитно-

го поля со скоростью υ// = υcosα. Одновременно частица равномерно вращается по окружности, плоскость которой перпендикулярна вектору B . Частица движется при этом с постоянной скоростью υ , радиус окружности равен:

Период обращения по окружности:

T = 2qπBm .

Траектория движения представляет винтовую линию с радиусом витка R и шагом винтовой линии, равным:

h = υ// T = υcosα 2qπBm .

51

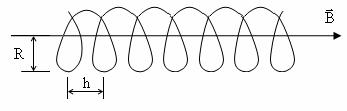
Шаг h есть расстояние, которое частица пролетает вдоль силовой линии магнитного поля за период обращения по окружности радиуса R .

4. Кинетическая энергия частицы в магнитном поле

Запишем и проанализируем выражение, связывающее работу магнитной силы и кинетическую энергию частицы:

dA = dWk ,

dWk = Fм drr = Fм υrdt = q[υr×B]υrdt = 0 , dWk = 0 , Wk = const .

Магнитная сила не совершает работы. Кинетическая энергия заряженной частицы в магнитном поле остается постоянной.

5. Циклотрон

Устройство, применяемое для получения пучков заряженных частиц с большими значениями энергии, называется ускорителем заряженных частиц.

Ускоритель, основанный на независимости периода обращения заряженной частицы в магнитном поле от ее скорости, называется циклотроном.

Прибор состоит из двух электродов в виде половинок круглой полой коробки. Электроды называются дуантами.

52

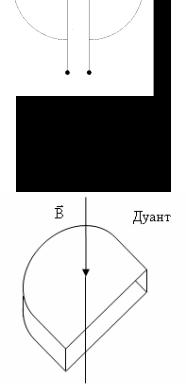
Дуанты помещаются в однородное магнитное поле, перпендикулярное к их плоскости. На дуанты подается переменное

напряжение с амплитудой Um . Частица движется по окружно-

сти, радиус которой пропорционален модулю скорости. Следовательно, с ростом υ радиус возрастает, и в результате траектория движения представляет собой раскручивающуюся спираль. Частота изменения напряжения между дуантами подбирается таким образом, что каждый раз, когда частица оказывается в зазоре между дуантами, она получает энергию от электрического поля:

∆Wk = qUm .

53

6. Эффект Холла в проводниках

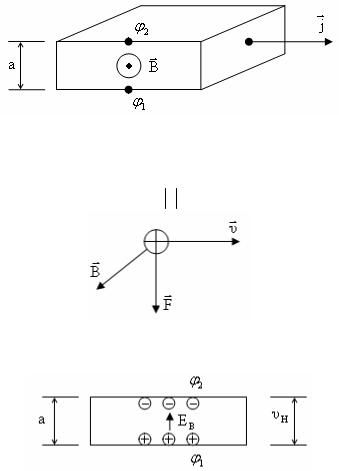
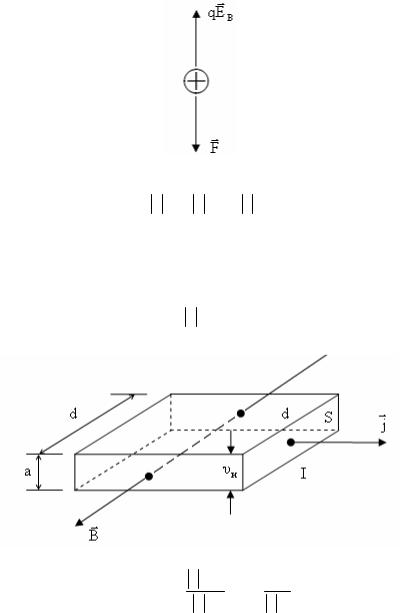
Пластина, вдоль которой течет постоянный электрический ток, находится в однородном магнитном поле так, что век-

торы B и j взаимно перпендикулярны. Толщина пластины a .

r Пусть:

υ– скорость упорядоченного движения положительно заряженных носителей тока. На каждый положительно заряженный носитель тока действует магнитная сила, направленная вниз

F = q υB .

В результате этого у носителей тока появляется составляющая скорости, направленная к нижней грани пластинке, где образуется избыток заряда.

При этом возникает однородное поперечное электрическое поле EB .

54

В конечном счете, действие этого поля на носители тока уравновешивает действие магнитной силы:

F = q E0 , q υB = q EB ,

EB = υB .

Между точками 1 и 2 возникает разность потенциалов:

(ϕ1 −ϕ2 )= EB a = a υB ,

υн = a υB ,

j = q n υ

I = jS = j a d.

Запишем:

υн = a υB = a qqnnυB = a qjn B ,

55

υн = q1n a j B ,

где:

q , n – модуль заряда заряд и концентрация носителей тока;

j – плотность тока.

Обозначим:

R н = q1n ,

υн = R н a j B .

Величина R н называется постоянной Холла. Запишем:

υн = R н a j B = R нa d j d1 B = R нSj Bd = R нdI B ,

υн = R нdI B ,

где:

I – сила тока в проводнике.

Глава 3 Магнитное поле в веществе

Намагниченность

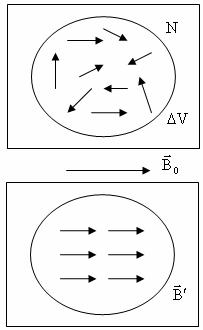
Установлено, что молекулы многих веществ имеют собственный магнитный момент Pm . Выделим физически малый объем вещества ∆V , в котором находится большое число молекул N .

56

Намагниченностью называется векторная величина, равная отношению магнитного момента физически малого объема вещества к этому объему:

Если внешнее магнитное поле отсутствует, то магнитные моменты молекулы ориентированы хаотично, следовательно:

∑N Prmi = 0 , i=1

J = 0 .

Поместим вещество во внешнее магнитное поле B0 . Под его действием магнитные моменты молекул ориентируются по направлению вектора B0 . В этом случае:

57

Вещество, намагниченность которого отличается от нуля, называется намагниченным. Вещество при этом называется магнетиком. Процесс, в результате которого магнетик приобретает намагниченность, называется намагничением.

Всякий магнитный момент создает магнитное поле. Намагниченный магнетик создает магнитное поле, магнитную инr -

дукцию которого обозначим B′. Магнитное поле магнетика B′ складывается с внешним магнитным полем B0 , при этом маг-

нитная индукция оказывается равной:

B = B0 + B′.

Запишем для однородного изотропного магнетика:

J = nPm .

Здесь:

n – концентрация молекул магнетика, имеющих магнитный мо-

мент Pm .

Магнетик намагничен однородно, если во всех его точках выполняется условие

J = const .

Молекулярные токи

Для объяснения существования магнитного момента у молекул вещества была предложена следующая модель.

В каждой молекуле вещества циркулирует круговой ток силой Im , названный молекулярным током. Молекулярный ток

обладает магнитным моментом:

Pm = ImSm nr,

где:

58

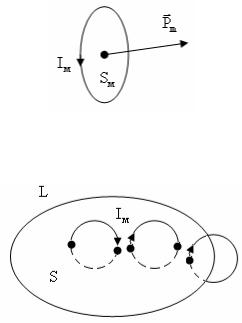
Sm – площадь, ограниченная током.

В однородном, изотропном и намагниченном магнетике проведем плоский контур L , ограничивающий поверхность S . Будем искать алгебраическую сумму сил молекулярных токов, охватываемых контуром L .

Видно, что имеются молекулярные токи, которые дважды пересекают поверхность S , причем в противоположных направлениях. Очевидно, что сумма таких молекулярных токов равна нулю. Следовательно, необходимо найти сумму сил токов, пересекающих поверхность S один раз.

Обозначим:

I′– алгебраическая сумма сил молекулярных токов, охватываемых произвольным контуром L :

N

I′ = ∑Imi .

i=1

Построим участок контура L , укажем направление обхода контура L . Выделим элемент контура dl . Построим косой цилиндр с основаниями, равными площади молекулярного тока Sm и образующей dl , совпадающей с участком контура.

59

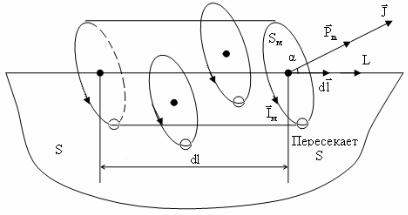
Введем элементарный вектор dl , направление которого совпадает с направлением обхода контура.

Обозначим:

α– угол между векторами Pm и dl .

Видно, что поверхность S , ограниченную контуром L , один раз пересекают молекулярные токи, центры которых находятся внутри построенного цилиндра.

Обозначим:

n – концентрация молекул магнетика;

dI′– алгебраическая сумма молекулярных токов, пересекающих S в пределах элемента контура dl .

Запишем:

dI′ = Im ndV , dV = Sm dl cosα,

dI′ = I m nS m dl cosα = (I m Sm )n cosα dl = = (Pm n)cosα dl = J cosα dl = rJ drl,

dI′ = J dl ,

где:

dV – объем цилиндра.

Интегрируем по всему контуру L :

60