
04_Магнетизм
.pdf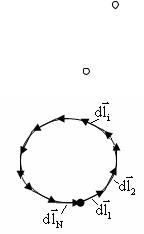
r |
N |
r |
|
N |
r r |
F = |
∑dFi |
= ∑I[dli ×B]= |
|||
|
i=1 |
|
|
i=1 |
r r . |
|
|
r |
|
r |
|
|
|
|
= I[(∫dl )×B] |
||
= I ∑dli |
×B |
||||
|
|
|
|
|
|
|
|
|
|
||
Видно, что: |
N |
r |
|
|
|
|
|
|
|
||
|
∑dli = 0 , ∫dl = 0 . |
||||
i=1
Следовательно:
F = 0 .
Результирующая сила, действующая на плоский контур в однородном магнитном поле равна нулю.
Обозначим:
dMi – момент сил, действующий на i -й участок контура отно-
сительно точки О. Очевидно:
dMi = [rri ×dFi ].
Суммарный (результирующий) момент сил, действующий на контур относительно той же точки О равен:
Mr = ∑N dMr i = ∫dMr = ∫[rr ×dFr].
i=1
41

Возьмем произвольную точку O′ так, чтобы: rr = b + rr′,
b = const , rr′ = rr − b .
Найдем момент сил относительно O′:
M′ = ∫[rr′×dF]= ∫[(rr − b)×dF]=
= ∫[rr ×dFr]− ∫[br×dFr]= Mr - [br×∫dFr].
Но:
∫dF = 0 ,
M′ = M .
Момент сил, действующий на плоский контур с током в однородном магнитном поле, не зависит от выбора точки, относительно которой он определяется.
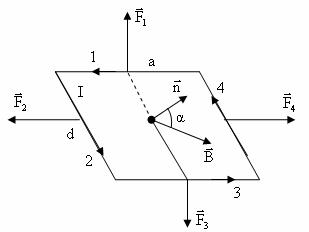
Пусть прямоугольный контур со сторонами a и d нахо-
дится в магнитном поле с индукцией B как показано на рисунке. В контуре протекает ток I .
42
Запишем:
F1 = I B a sin900 = I B a , F2 = I B d cosα,
F3 = I B a sin900 = I B a ,
F4 = I B d cosα.
Кроме того:
F1 = −F3 ,
r F2 = −F4 .
Силы F1 и F3 лежат в различных плоскостях и создают пару
сил, момент которой равен:
M13 = F1 l ,
где:
l – плечо пары сил.
43

Из рисунка видно, что:
l = dsinα,
M13 = I B a d sinα = I B S sinα = I S B sinα.
Пара сил F2 и F4 лежат в одной плоскости, поэтому:
M24 = 0 .
На контур с током со стороны магнитного поля действует момент сил, равный:
M = I S B sinα = Pm Bsinα, Pm = IS.
С учетом направлений M , Pm и B запишем:
M = [Pm ×B], M = Pm Bsinα.
44
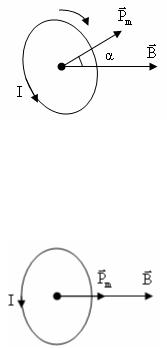
Здесь:
α– угол между вектором магнитного момента контура и вектором магнитной индукции поля.
Момент сил M стремится повернуть поверхность так, чтобы магнитный момент контура Pm оказался параллельным вектору индукции B .
При этом оказывается, что при α = 0 имеем:
M = Pm Bsinα = 0 .
Контур будет находиться в состоянии устойчивого равновесия.
2. Контур с током в неоднородном магнитном поле
Рассмотрим качественно поведение контура с током в неоднородном магнитном поле, B ≠ const .
45
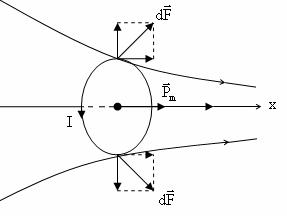
r
Силаr dF , действующая на элемент контура, перпендикулярна к B . При этом существует составляющая силы в на-
правлении, в котором происходит увеличение модуля B . Анализируя действие магнитного поля на различные элементы контура, можно прийти к выводу о том, что результирующая сила
F , действующаяr на контур, направлена также в сторону возрастания модуля B .
Расчеты дают для силы F закон: |
|
|
|
|||||||
r |
r r |
∂B |
r r |
∂B |
r r |
|
∂B |
|||
F = i P |
|
|
+ j P |
|
|
+ k P |
|
. |
||
|
|
|
||||||||
|
m |
|
|
m |
|
|
|
m |
|
|
|
|
∂x |
|
∂y |
|
|
∂z |
|||
Магнитная сила
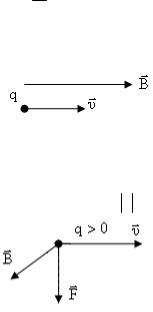
Из опыта известно, что на заряд q , движущийся в маг-
нитном поле, действует сила, равная:
F = q[υr×B].
υr |
Здесь: |
– вектор скорости заряда q ; |
B – магнитная индукция.
46
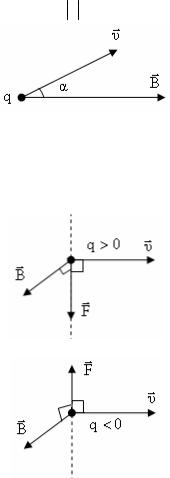
Величина F называется магнитной силой. Модуль магнитной силы равен:
F = q υBsinα.
Здесь:
α– угол между векторами υ и B .
Вектор F перпендикулярен как вектору скорости υ, так и век-
тору магнитной индукции B . Кроме того, направление F определяется с учетом знака заряда частицы q .
Если имеютсяr одновременно электрическое поле E и
магнитное поле B , то сила, действующая на заряженную частицу, равна:
F = qE + q[υr×B].
r
Вектор F называется силой Лоренца.
47
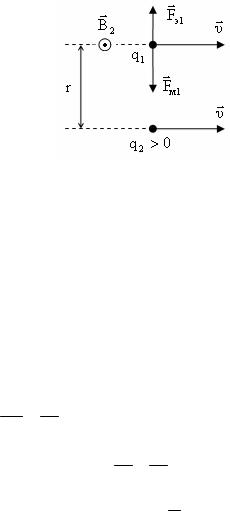
Рассмотрим два одноименно заряженных точечных заряда q1 и q2 , движущихся вдоль параллельных прямых со скоро-
стью υ.
Рассмотрим силы,
Fм1 = µ0
Fэ1 4π
действующие на заряд q1 : |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
F |
|
= |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
q2 |
|
|
|
, |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4πε |
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
э1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Fм1 = |
|
q1 |
|
υB2sinα , |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
r |
|
|
|
|
= |
|
µ |
|
0 |
|
|
|
q |
2 |
[υ× r] |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
B |
|
|
|
= |
µ |
0 |
|
|
|
q2 |
|
υ |
= |
|
π |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, α |
|
|
|
|
|
, |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
4π |
|
|
|
|
|
|
r2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
F |
|
= |
|
|
µ |
0 |
|
|
|
|
|
|
|
q1 |
|
|
|
q2 |
|
|
υ2 |
, |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
м1 |
|
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
q1 |
|
|
|
q2 |
|
υ2 |
4πε0 r2 |
= ε |
0µ0 υ |
2 |
= |
υ2 |
, |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
r |
2 |
|
q1 |
|
|
|
q2 |
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Fм = υ2 , Fэ c2
с = 3 108 мс .
Полученный результат указывает на то, что при «медленном» движении магнитная сила существенно меньше, чем сила электростатического поля.
48
Движение заряженной частицы в магнитном поле
1. Скорость частицы параллельна вектору индукции магнитного поля
F = qυBsinα , α = 0 , F = 0 , a = mF = 0 , υ = const .
Частица движется прямолинейно с постоянной скоро-
стью.
2. Скорость частицы перпендикулярна вектору индукции магнитного поля
υr B , F υr , F = q υB .
Сила F сообщает частице нормальное ускорение:
a n = |
F |
= |
|
q |
υB |
, a n = |
υ2 |
, |
||||||||||
|
|
|
||||||||||||||||
m |
m |
R |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
q |
|
υB |
= |
|
υ2 |
, R = |
mV |
. |
|
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
m |
|
R |
|
q |
B |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
49
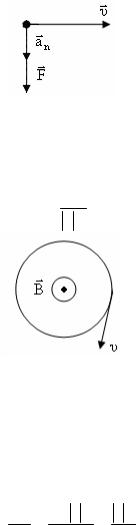
Нормальное ускорение не изменяет модуль скорости υ. Следовательно, в однородном магнитном поле, частица будет двигаться по кривой с постоянным радиусом кривизны, т.еr. по
окружности, плоскость которой перпендикулярна вектору B , а радиус равен:
R = mVq B .
Отношение |
|
q |
называется удельным зарядом частицы. Найдем |
||||||||||
|
|||||||||||||
m |
|||||||||||||
период обращения частицы по окружности: |
|||||||||||||
|
|
|
T = |
2π R |
= 2π |
|
m |
υ |
= |
2π m |
. |
||
|
|
|
υ |
|
|
|
|
||||||
|
|
|
q |
υ |
|
|
q |
B |
|||||
|
|
|
|
|
|
|
|
||||||
Циклическая (круговая) частота вращения частицы рав-
на:
ω= 2Tπ = 22ππqmB = qmB .
3.Скорость частицы направлена под углом к индукции магнитного поля
Векторы υr и B образуют угол α.
50
