Математика для економістів Заоч. Ч 1 2015

Тема 3. Елементи матричного аналізу План заняття

З даної теми передбачається вивчення таких питань:

-матричний запис та матричний спосіб розв’язання системи лінійних алгебраїчних рівнянь;

-лінійні оператори;

-власні вектори та власні значення;

-квадратичні форми;

-приклади застосування матричного аналізу в економіці.

Навчальні цілі

Вивчення теми надасть студентам можливість виробити практичні навички щодо матричного запису системи лінійних рівнянь та матричного способу розв’язання системи лінійних рівнянь, знати поняття лінійних операторів, власних векторів і власних значень, ознайомитись із застосуванням матричного аналізу в економіці.

Методичні рекомендації до практичного заняття

Матричний метод рішення систем лінійних рівнянь Матричний метод застосовується до розв’язку систем рівнянь, де

кількість рівнянь дорівнює кількості невідомих.

Метод є зручним для розв’язку систем невисокого порядку. Метод базується на застосуванні властивостей множення матриць. Нехай задано систему рівнянь:

що може бути пов’язано з розрахунковими складностями при розв’язку систем високого порядку.

40

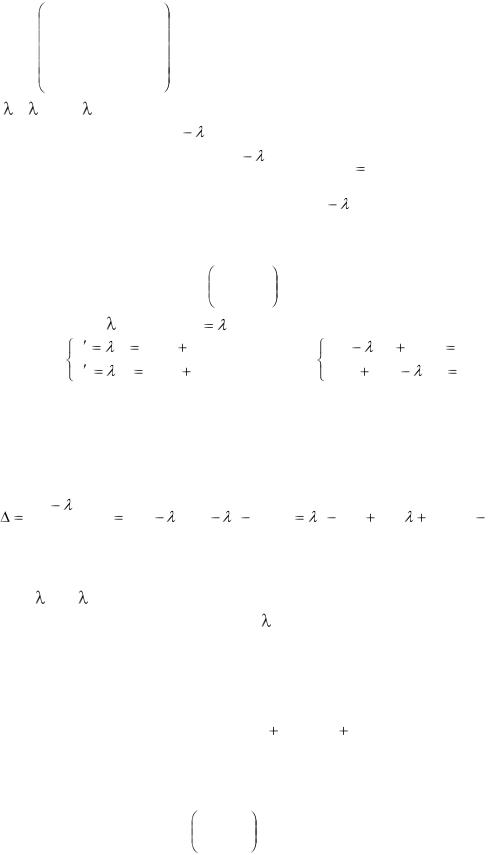
При цьому число 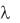називається власним значенням (характеристичним числом) матриці А, яке відповідає вектору х .

Означення. Якщо задана квадратна матриця

Це рівняння називається характеристичним рівнянням, а його ліва частина - характеристичним многочленом матриці А.

Так як власний вектор x ненульовий, то х1 і х2 не дорівнюють нуль одночасно. Так як дана система однорідна, то для того, щоб вона мала нетривіальний розв’язок, визначник системи має дорівнювати нулю. В протилежному випадку за правилом Крамера система має єдиний розв’язок – нульовий, що неможливо.

рівнянь при підстановці в неї значення .

Якщо характеристичне рівняння не має дійсних коренів, то матриця А не має власних векторів.

Квадратичні форми Означення. Однорідний многочлен другого степеня відносно змінних х1 і х2

який не містить довільного члена і невідомих в першому степені, називається

визначником квадратичної форми.

41

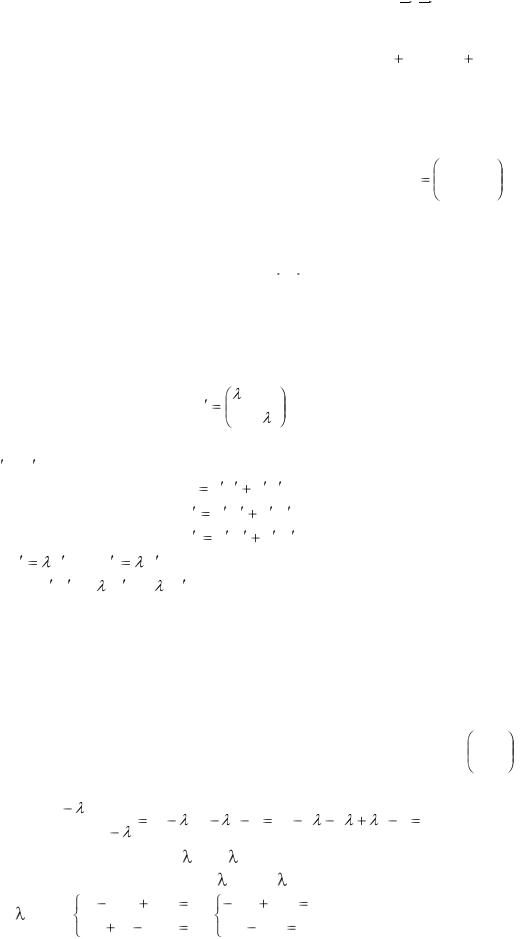
Нехай на площині задано ортогональний базис е1 , е2 . Кожна точка площини має в цьому базисі координати х1, х2.

Якщо задана квадратична форма Ф(х1, х2) = а11 x12 2a12 x1 x2 a22 x22 , то її можна розглядати як функцію від змінних х1 і х2.

Зведення квадратичних форм до канонічного виду

Це симетричне перетворення можна записати у вигляді:

y1 = a11x1 + a12x2 y2 = a12x1 + a22x2

де у1 і у2 – координати вектора Ах в базисі е1 , е2 .

Очевидно, що квадратична форма може бути записана у вигляді:

Ф(х1, х2) = х1у1 + х2у2.

Якщо в якості базису взяти сукупність власних векторів лінійного перетворення, то в цьому базисі матриця лінійного перетворення має вигляд:

Вираз Ф(х1, х2 ) 1(х1)2 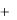2 (х2 )2 називається канонічним видом квадратичної форми. Аналогічно можна привести до канонічного виду квадратичну форму з більшою кількістю змінних.

Теорія квадратичних форм використовується для зведення до канонічного виду рівнянь кривих і поверхонь другого порядку.

42

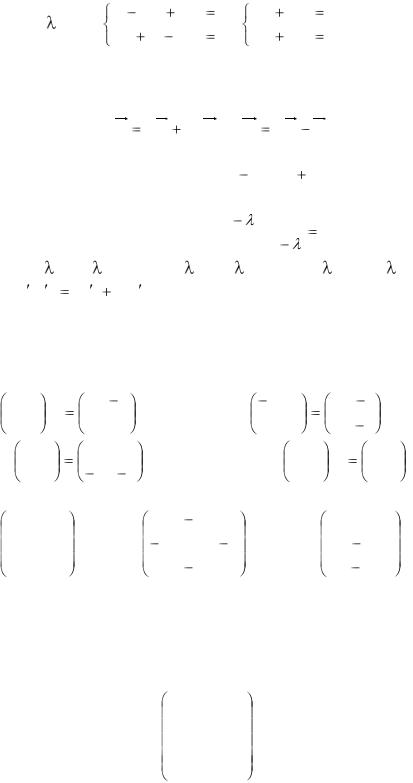
Із системи отримаємо залежність: x1 – 2x2 = 0. Власні вектори для першого кореня характеристичного рівняння мають координати: (t; 0,5t) де t- параметр.

Із системи отримаємо залежність: x1 + x2 = 0. Власні вектори для другого кореня характеристичного рівняння мають координати: (t; -t) де t- параметр.

Отримані власні вектори можна записати у вигляді:

2. Знайти власні значення і власні вектори матриці:

3. Підприємство випускає 4 види виробів з використанням чотирьох видів сировини. Норми використання сировини представлені елементами матриці А:

Знайти витрати сировини кожного виду виробу: відповідно 60, 50, 35 та 40 одиниць.

Питання для самоконтролю

1.Опишіть алгоритм розв'язування системи лінійних рівнянь матричним способом.

43

2.Що називається власним значенням та власним вектором матриці ?

3.Що називається квадратичною формою?

4.Наведіть приклади застосування матричного аналізу в економіці.

Рекомендована література [1,2,4]

Тема 4. Елементи векторної алгебри та аналітичної геометрії План заняття

1.Вектор, довжина вектора, властивості векторів.

2.Дії над векторами.

3.Поняття базису. Система координат.

4.Скалярний, векторний, мішаний добутки векторів.

5.Геометричне застосування добутків векторів.

6.Рівняння прямої на площині.

7.Кут між прямими на площині.

8.Відстань від точки до прямої на площині.

Навчальні цілі

Вивчення теми надасть студентам можливість знати елементи векторної алгебри, зокрема такі поняття, як вектори, базис, вміти виконувати дії з векторами, обчислювати скалярний, векторний, мішаний добутки векторів. Також ознайомитись з елементами аналітичної геометрії на площині, вивчити види рівнянь прямої на площині, умови паралельності і перпендикулярності прямих на площині, вміти визначати кут між двома прямими.

Методичні рекомендації до практичного заняття

Елементи векторної алгебри Означення. Вектором називається направлений відрізок (впорядкована

пара точок). До векторів відноситься також і нульовий вектор, початок і кінець якого співпадають.

Означення. Довжиною (модулем) вектора називається відстань між початком і кінцем вектора.

АВа

Означення. Вектори називаються колінеарними, якщо вони розташовані на одній або паралельних прямих. Нульовий вектор є колінеарним будь-якому вектору.

Означення. Вектори називаються компланарними, якщо існує площина, якій вони паралельні.

Колінеарні вектори завжди компланарні, але не всі компланарні вектори колінеарні.

Означення. Вектори називаються рівними, якщо вони колінеарні, однаково направлені і мають одинакові модулі.

Всякі вектори можна привести до спільного початку, тобто побудувати вектори, відповідно рівні даним і які мають спільний початок. Із означення

44

рівності векторів випливає, що будь-який вектор має нескінченно багато векторів, що дорівнюють йому.

Означення. Лінійними операціями над векторами називається сума і множення на число.

Означення. 1) Базисом в просторі називаються будь-які 3 не компланарних вектора, які взяті у визначеному порядку.

2)Базисом на площині називаються будь-які 2 не колінеарні вектори, які взяті у визначеному порядку.

3)Базисом на прямій називається будь-який ненульовий вектор.

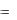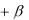Означення. Якщо e1 , e2 , e3 - базис в просторі і a e1 e2 e3 , то числа

-рівні вектори мають одинакові координати;

-при множення вектора на число його компоненти також множаться на це число:

називаються лінійно незалежними.

Властивість 1. Якщо серед векторів ai є нульовий вектор, то ці вектори лінійно залежні.

45

Властивість 2. Якщо до системи лінійно залежних векторів додати один або декілька векторів, то отримана система також буде лінійно залежна.

Властивість 3. Система векторів лінійно залежна тоді і лише тоді, коли один з векторів розкладається в лінійну комбінацію решти векторів.

Властивість 4. Будь-які 2 колінеарних вектора лінійно залежні і, навпаки, будь-які 2 лінійно залежні вектори колінеарні.

Властивість 5. Будь-які 3 компланарних вектора лінійно залежні і, навпаки, будь-які 3 лінійно залежні вектори компланарні.

Властивість 6. Будь-які 4 вектора лінійно залежні.

Система координат

Для визначення положення довільної точки можуть використовуватись різні системи координат. Положення довільної точки в деякій системі координат повинно однозначно визначатись. Поняття системи координат являє собою сукупність точки початку відліку (початок координат) і деякого базису. Як на площині, так і в просторі можливо завдання самих різноманітних систем координат. Обрання системи координат залежить від характеру поставленої геометричної, фізичної або технічної задачі.

Декартова система координат

Зафіксуємо в просторі точку О і розглянемо довільну точку М.

Вектор ОМ назвемо радіус-вектором точки М. Якщо в просторі задати деякий базис, то точці М можна сопоставити деяку трійку чисел – координати її радіусвектора.

Означення. Декартовою системою координат в просторі називається сукупність точки і базису. Точка називається початком координат. Прямі, що проходять через початок координат називаються осями координат.

1-я вісь – вісь абсцис; 2-я вісь – вісь ординат; 3-я вісь – вісь аплікат.

Щоб знайти координати вектора треба із координат його кінця відняти координати початку.

Якщо задані точки А(x1,y1,z1), B(x2,y2,z2), то АВ = (x2 –x1, y2 –y1, z2– z1).

Означення. Базис називається ортонормованим, якщо його вектори

попарно ортогональні і дорівнюють одиниці.

Означення. Декартова система координат, базис якої ортонормований називається декартовою прямокутною системою координат.

Довжина вектора в координатах визначається як відстань між точками початку і кінця вектора. Якщо задані дві точки в просторі А(х1, y1, z1), B(x2, y2,

46

Лінійні операції над векторами в координатах

Нехай задані вектори в прямокутній системі координат

a(xA , y A , z A ); b(xB , yB , zB ), тоді лінійні операції над ними в координатах мають вид:

Використовуючи отримані рівності, отримаємо формулу для обчислення косинуса кута між векторами:

c

b

a

Властивості векторного добутку векторів:

47

6) геометричним змістом векторного добутку векторів є площа паралелограма,

a

c

b

48

Рівняння прямої на площині Означення. Будь-яка пряма на площині може бути задана рівнянням

першого порядку

Ах + Ву + С = 0, Причому константи А, В не дорівнюють нулю одночасно, тобто А2 + В2 0. Це

рівняння першого порядку називають загальним рівнянням прямої.

-В = С = 0, А 0 – пряма співпадає з віссю Оу;

-А = С = 0, В 0 – пряма співпадає з віссю Ох.

Рівняння прямої може бути представлено в різних видах в залежності від будь-яких заданих початкових умов.

Рівняння прямої по точці і вектору нормалі Означення. В декартовій прямокутній системі координат вектор з

координатами (А, В) перпендикулярний прямій , що задана рівнянням Ах + Ву

+ С = 0.

Рівняння прямої, що проходить через дві точки

Нехай на площині задані дві точки M1(x1, y1) и M2(x2, y2), тоді рівняння прямої, що проходить через ці точки:

49