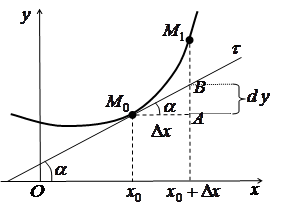- •Формула скалярного добутку векторів для плоских задач
- •Формула скалярного добутку векторів для просторових задач
- •Формула скалярного добутку n -вимірних векторів
- •Властивості скалярного добутку векторів
- •Властивості
- •Нормальне рівняння прямої
- •Відстань від точки до прямої на площині.
- •Відстань від точки до прямої в просторі.
- •Рівняння площини, що проходить через точку, перпендикулярно вектору нормалі
- •Нормальне рівняння площини
- •Канонічне рівняння прямої
- •Вертикальні асимптоти
- •Похилі асимптоти
- •Горизонтальні асимптоти
- •Необхідна ознака локального екстремуму:
- •Достатня ознаки існування екстремуму функції
Нормальне рівняння прямої
![]()
Знак
радикала вибирається із умови, що ![]() ,
де
,
де ![]() .
Якщо ввести позначення:
.
Якщо ввести позначення:
![]()
то розглядуване рівняння записується
![]() .
.
Для
знаходження відстані ![]() точки
точки ![]() до
прямої
до
прямої ![]() застосовується
формула
застосовується
формула
![]() .
.
Відстань від точки до прямої на площині.
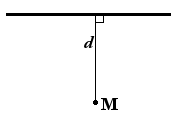
Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.
Якщо задане рівняння прямої Ax + By + C = 0, то відстань від точки M(Mx,My) до прямої можна знайти, використавши наступну формулу
|
d= |
|A·Mx+ B·MyC| |
|
√A2+ B2 |
Відстань від точки до прямої в просторі.
Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.
Якщо s ={m;n;p} - напрямний вектор прямої l, M1(x1, y1, z1) - точка що належить прямій, тоді відстань від точки M0(x0, y0,z0) до прямої lможна знайти, використовуючи формулу
|
d= |
|M0M1×s| |
|
|s| |
18. Рівняння площини, яка проходить через точку М0(х0, у0, z0)
перпендикулярно до вектора n (A, B,C).
Рівняння площини, що проходить через точку, перпендикулярно вектору нормалі
Щоб скласти рівняння площини, за координатами точки площини M(x0, y0, z0) і вектора нормалі площини n = {A; B; C}
можна використати наступну формулу.
A(x - x0) + B(y - y0) + C(z - z0) = 0
19. Рівняння площини у відрізках на осях.
Якщо площина перетинає осі OX, OY і OZ в точках з координатами (a, 0, 0), (0, b, 0) і 0, 0, с), то вона може бути знайдена, якщо використати формулу рівняння площини в відрізках
|
x |
+ |
y |
+ |
z |
= 1 |
|
a |
b |
c |
20. Нормальне рівняння площини. Відстань від точки до площини.
Нормальне рівняння площини
![]() ,
де
,
де ![]() –
радіус-вектор довільної точки
–
радіус-вектор довільної точки ![]() площини,
площини, ![]() –
одиничний вектор, що має напрям
перпендикуляра, опущеного на площину
із початку координат,
–
одиничний вектор, що має напрям
перпендикуляра, опущеного на площину
із початку координат, ![]() –
кути, утворені згаданим перпендикуляром
з осями координат
–
кути, утворені згаданим перпендикуляром
з осями координат ![]() ,
, ![]() –
довжина перпендикуляра.
–
довжина перпендикуляра.
В
координатній формі рівняння записується ![]()
Відстань
від точки до площини знаходять за
формулою
![]()
21. Кут між двома площинами.
Двогранний кут між площинами дорівнює куту утвореному нормальними векторами цих площин.
Двогранний кут між площинами дорівнює куту утвореними прямими l1 і l2, що лежать в відповідних площинах і перпендикулярні лінії перетину площин.Якщо задані рівняння площин A1x + B1y + C1z + D1 = 0 і A2x + B2y + C2z + D2= 0, то кут між площинами можна знайти, використавши наступну формулу
|
cos α =
|
|A1·A2 + B1·B2 + C1·C2| |
|
(A12 + B12 + C12)1/2(A22 + B22 + C22)1/2 |
22. Параметричні рівняння прямої в просторі. Канонічні рівняння прямої в
просторі.
Канонічне рівняння прямої
![]() –
називається
канонічним рівнянням прямої, яка
проходить через точку
–
називається
канонічним рівнянням прямої, яка
проходить через точку ![]() паралельно
до вектора
паралельно
до вектора ![]() ,
який називається напрямним.
,
який називається напрямним.
Параметричні рівняння прямої
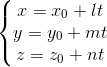 —
параметричні
рівняння прямої, де параметр
—
параметричні
рівняння прямої, де параметр ![]() .
Ці рівняння одержують із канонічного
рівняння прямої.
.
Ці рівняння одержують із канонічного
рівняння прямої.
23. Рівняння прямої в просторі, яка проходить через дві задані точки М1(х1,
у1, z1) і М2(х2, у2, z2).
Рівняння прямої, що проходить через дві різні точки в просторі
Якщо пряма, що проходить через дві точки A(x1, y1, z1) і B(x2, y2, z2), такі що x1 ≠ x2, y1 ≠ y2 і z1 ≠ z2 то рівняння прямої можна знайти, якщо використати наступну формулу
|
x -x1 |
= |
y-y1 |
= |
z -z1 |
|
x2 -x1 |
y2 -y1 |
z2 -z1 |
24. Умови паралельності і перпендикулярності прямих в просторі.
Умова паралельності прямих
![]()
або
![]()
Умова перпендикулярності прямих
![]()
або
![]()
25. Кут між прямою і площиною. Умови паралельності і перпендикулярності
прямої і площини.
Кут між прямою та площиною — це кут між прямою та її проекцією на цю площину
Формула обчислення кута між прямою та площиною
Якщо в просторі задані напрямний вектор прямої Ls = {l; m; n}і рівняння площини
Ax + By + Cz + D = 0,
то кут між цією прямою і площиною можна знайти використав формулу
|
sin φ= |
| A · l + B ·m + C ·n | |
|
√A2 + B2 + C2 · √l2 +m2 +n2 |
26. Еліпс, його рівняння.
Еліпсом називають множину всіх точок площини, сума відстаней яких від двох даних точок цієї площини, які називаються фокусами, є величина стала і більша від відстані між фокусами.

![]()
27. Гіпербола, її рівняння.
Гіпербола — крива другого порядку з ексцентриситетом більшим за одиницю.
Каноническое
уравнение гиперболы имеет вид ![]() ,
где
,
где ![]() –
положительные действительные числа.
–
положительные действительные числа.
28. Парабола, її рівняння.
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы).
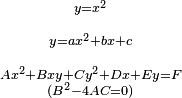
29. Множина. Функції, послідовності, границя послідовності.
30. Границя функції. Основні теореми.
31. Похідна функції. Диференціал функції. Геометричний зміст похідної і
диференціалу.
Похідною
функції y = f(x) у точці Х називають число,
до якого прямує відношення
![]()
Диференціал в математиці — головна лінійна частина приросту функції або відображення
![]() де
dy/dx позначає похідну від y по
змінній x.
Ця
формула
підсумовує
інтуїтивне
твердження,
що
похідна y по
змінній x це
границя
відношення
приростів
Δy/Δx де
Δx прямує
до
нуля.
де
dy/dx позначає похідну від y по
змінній x.
Ця
формула
підсумовує
інтуїтивне
твердження,
що
похідна y по
змінній x це
границя
відношення
приростів
Δy/Δx де
Δx прямує
до
нуля.
Геометричний зміст похідної: значення похідної функції y = f(x) у точці x0 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x0: y' = f'(x0) = k = tgα.
Геометричний зміст диференціала
Нехай ![]() ,
,![]() та
існує
та
існує![]() .
За означенням диференціала
.
За означенням диференціала![]() .
.
|
|
Скористаємося
геометричним змістом похідної:
З
трикутника
Отже,
диференціал функції
|
32. Основні теореми диференціального числення.
Теорема Ферма
Нехай
функція ![]() визначена
на інтервалі
визначена
на інтервалі![]() і
в деякій точці
і
в деякій точці![]() має
найбільше або найменше значення. Тоді
якщо в точці
має
найбільше або найменше значення. Тоді
якщо в точці![]() існує
похідна, то вона дорівнює нулю, тобто
існує
похідна, то вона дорівнює нулю, тобто![]() .
.
Теорема Ролля
Якщо
функція ![]()
1)
неперервна на відрізку ![]() ,
,
2)
має рівні значення ![]() на
кінцях цього відрізка,
на
кінцях цього відрізка,
3)
диференційовна в усіх точках інтервалу ![]() ,
,
то
в цьому інтервалі існує принаймні одна
точка ![]() ,
,![]() ,
в якій похідна функції дорівнює нулю
,
в якій похідна функції дорівнює нулю
![]() .
.
Теорема Лагранжа (теорема про скінченні прирости)
Якщо
функція ![]()
1)
неперервна на відрізку ![]() ,
,
2)
диференційовна в інтервалі ![]() ,
,
то
в цьому інтервалі існує принаймні одна
така точка ![]() ,
,![]() ,
що має місце рівність:
,
що має місце рівність:
![]() .
.
Теорема Коші (Cauchy theorem) (про відношення приростів двох функцій)
Якщо
функції ![]() і
і![]()
1)
неперервні на відрізку ![]() ,
,
2)
диференційовані в інтервалі ![]() ,
причому
,
причому![]() ,
,
то
в цьому інтервалі існує точка ![]() ,
,![]() така,
що має місце рівність:
така,
що має місце рівність:
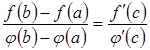 .
.
Правила Лопіталя розкриття невизначеностей
(І правило Лопіталя). Якщо:
1)
функції ![]() і
і![]() диференційовні
на інтервалі
диференційовні
на інтервалі![]() ,
,![]() для
всіх
для
всіх![]() ;
;
2) ![]() ;
;
3)
існує скінченна або нескінченна
границя 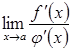 ,
,
то
існує границя 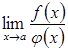 ,
причому має місце рівність:
,
причому має місце рівність:
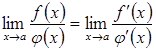 .
.
33. Обчислення границь за правилом Лопіталя.
Правила Лопіталя розкриття невизначеностей
(І правило Лопіталя). Якщо:
1)
функції ![]() і
і![]() диференційовні
на інтервалі
диференційовні
на інтервалі![]() ,
,![]() для
всіх
для
всіх![]() ;
;
2) ![]() ;
;
3)
існує скінченна або нескінченна
границя 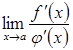 ,
,
то
існує границя 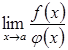 ,
причому має місце рівність:
,
причому має місце рівність:
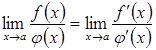 .
.
34. Формули Тейлора і Маклорена.
![]()
Полученное
выражение называется формулой
Маклорена для
многочлена ![]() степени
степени ![]() .
.
![]()
Это
выражение называется формулой
Тейлора для
многочлена ![]() в
окрестности точки
в
окрестности точки ![]() .
.
35. Область визначення функції. Неперервність функції. Точки розриву 1-го
та 2-го роду.
Область визначення - множина допустимих значень аргументу функції. Позначатиметься як D(y), якщо вказується область визначення функції y=f(x).
Якщо
задана: числова множина ![]() та
правило
та
правило ![]() ,
що дозволяє поставити у відповідність
кожному елементу
,
що дозволяє поставити у відповідність
кожному елементу ![]() з
множини
з
множини ![]() певне
число, то говорять, що задана функція
певне
число, то говорять, що задана функція ![]() з областю
визначення
з областю
визначення ![]() .
.
Тобто, визначення області значень є необхідна умова для визначення функції.
Функція ![]() називаєтьсянеперервною в
точці
називаєтьсянеперервною в
точці ![]() (continuous function at point),
якщо:
(continuous function at point),
якщо:
1) вона визначена в цій точці і в деякому її околі;
2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:
![]() ,
або
,
або ![]()
Функція ![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці ![]() ,
якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці
,
якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці![]() ,
тобто
,
тобто
![]() .
.
Точка х0 називається точкою
розриву першого роду функції у
= f(x), якщо
існують скінчені односторонні границі
справа
![]() та
зліва
та
зліва
![]()
Точка х0 називається точкою
розриву другого роду функції у=
f(x), якщо
границя справа ![]() або
зліва
або
зліва ![]() не
існує або нескінченна.
не
існує або нескінченна.
36. Асимптоти функції.