ЛЕКЦИЯ 8 З-н сохр.эн 4ч

ЛЕКЦИЯ 8. (4.3). СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СРЕДСТВ ИЗМЕРЕНИЙ НА ОСНОВАНИИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ

Уравнения математических моделей преобразователей или дру­гих связанных систем, выполняющих, например, преобразование энергии одного вида в другой, можно получить, используя два под­хода.

Во-первых, исходя из положения, что динамическая траектория системы определяется путем нахождения экстремума некоторых интегральных функций (интегральный принцип). В этом случае вначале устанавливается общая терминология для всех типов преобразователей: электрических, механических, химических, теп­ловых и т. д. введением энергетических функций (силовых функций) от обобщенных переменных. Затем, используя один из основных принципов, например принцип Гамильтона или получаемые из него уравнения Лагранжа, находят динамические уравнения для всех преобразователей, включая уравнения всех связей.

Во-вторых, используются бесконечно малые изменения в изме­рительной цепи (дифференциальный принцип). В этом случае урав­нения движения преобразователей получают на основании зако­нов физики, используя при этом, например, для получения механи­ческих сил электрического происхождения принцип возможных перемещений и закон сохранения энергии или плотность сил элек­тромагнитного ПОЛЯ.

С точки зрения формализации и сложности трудно отдать пред­почтение какому-либо из этих методов. Получение динамических уравнений на основании законов физики и принципа возможных пе­ремещений, очевидно, наименее формально. Но когда рассматри­вается сложная измерительная цепь, содержащая большое коли­чество переменных, необходимы интуиция и изобретательность. Интегральный метод является наиболее мощным методом механики, однако очень формализован, а потому физическая ясность задачи мо­жет быть затенена математическими выкладками.

Сущность и применение метода составления уравнений матема­тических моделей с использованием принципа возможных переме­щений и закона сохранения энергии рассмотрим на примере изме­рительных цепей, содержащих механические, электростатические, электромагнитные и электромеханические преобразователи.

В процессе физического описания СИ или составления структур­ной схемы в измерительной цепи выделим преобразователи механи­ческих величин в механические и электрических в электрические. Такими будут механические преобразователи, в которых не появляются силы электрического происхождения, а в электрических цепях не про­является эффект механического движения. Кроме того, выделим преобразователи или часть измери­тельной цепи, содержащие поля связей. Тогда для механической ча­сти измерительной цепи уравне­ния можно получить, исходя из принципа Д'Аламбера:

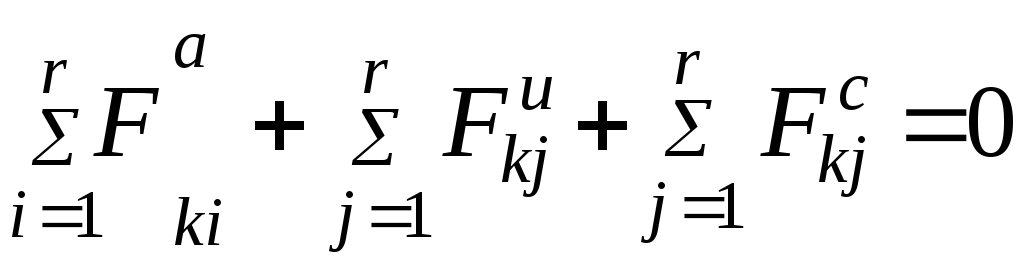( 4.1)

где — i-я внешняя сила, при­ложенная к k-му узлу; — j-я - инерционная сила k-го узла; — j-я механическая сила, вклю­чающая любые силы связи, приложенная к k-му узлу.

Принцип динамического равновесия (4.1) необходимо дополнить также соотношениями непрерывности пространства

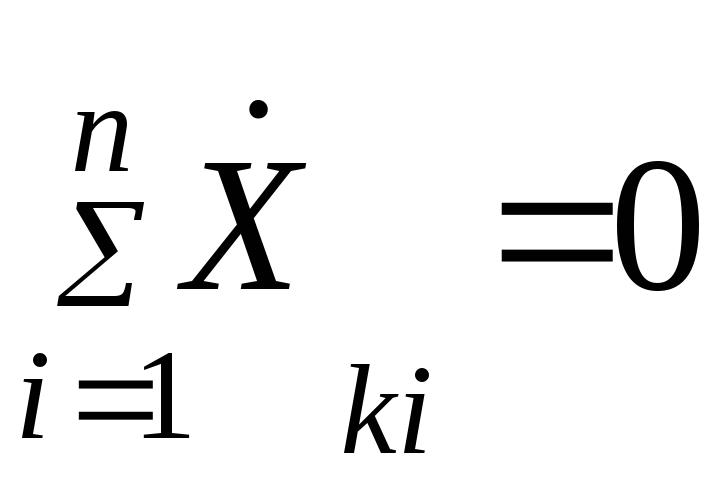(4.2)

где — i-я скорость в k-м механическом контуре.

Аналогично принципу динамического равновесия (4.1) и соот­ношениям непрерывности пространства (4.2) для электрической части цепи уравнения можно получить на основании двух правил [44] Кирхгофа:

правила узлов

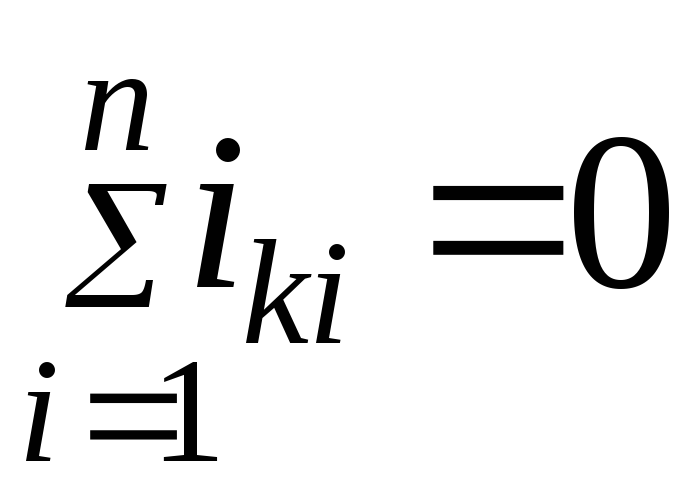(4.3)

правила контуров

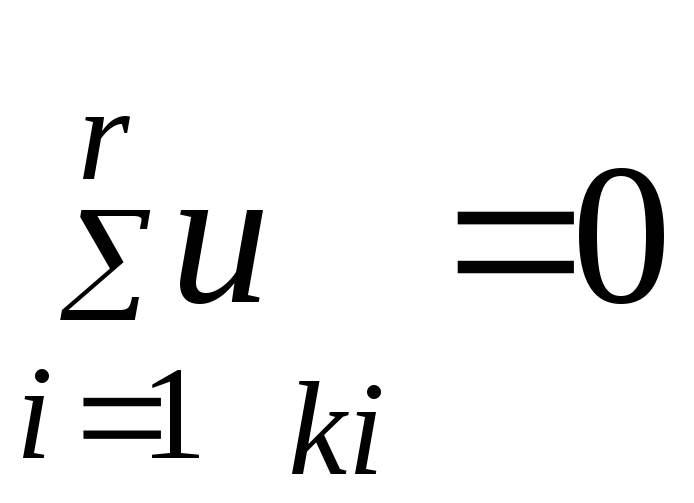(4.4)

где — i-й ток в к-м узле; — i-е напряжение в k-м контуре.

Для электрической части цепи в зависимости от ее разновиднос­тей могут быть также использованы законы Ома, Кулона и Фарадея.

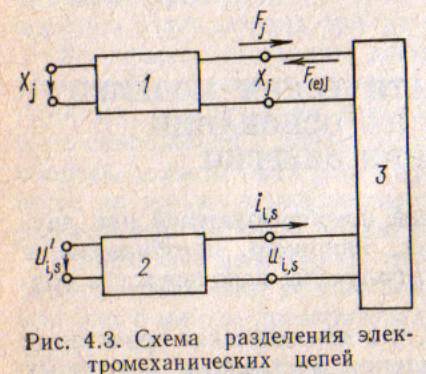
В измерительной цепи или преобразователях, содержащих по­ля связей, выделим три схемы (рис. 4.3): 1 — внешняя механиче­ская схема; 2 — внешняя схема, содержащая элементы-накопите­ли энергий электрического и магнитного полей; 3 — консерватив­ная электромеханическая схема, содержащая только поля связей — электрические и магнитные. На механические зажимы схемы 3 поступают силы или, иначе говоря, проявляется эф­фект механического движения в электрических цепях полей связи. С другой стороны, на эти зажимы со схемы 3 поступают силы электрического происхождения (электромеханической связи). На зажимы , связанные с накопителями энергии электри­ческого поля, и , связанные с накопителями энергии магнитного поля, поступают энергии со схем 2 и 3 как следствие механического движения.

Для составления уравнений механической 1 и электрической 2 схем можно использовать, например, принцип Д'Аламбера и урав­нения Кирхгофа. В эти схемы могут быть включены и другие пре­образователи: механические, электрические. Однако они не соеди­няются со схемой 3, как не содержащие полей связи, и в множества i,j,s не входят. Согласно схеме рис. 4.3, остаются неизвестными си­лы связи и энергии, или эффект механического движения, про­являющийся в полях связей схемы 3. Определим их.

Если электромеханическая измерительная цепь может быть представлена сосредоточенными параметрами, то

(4.5)

где W — полная накопленная энергия в связанной схеме 3 (рис. 4.3); — накопленная энергия электрических полей свя­зи; — накопленная энергия магнитных полей связи. Кроме то­го. запасенная энергия должна быть силовой функцией — одно­значной функцией переменных и независимой от динамического со­стояния и предыстории [42], иными словами, функцией мгновенной конфигурации цепи:

(4.6)

где — напряжение и заряд 1-й емкости:

(4.7)

(4.8)

— потокосцепление и ток в 5-й индуктивности:

(4.9)

(4.10)

— механические перемещения и сила:

(4.11)

(4.12)

Поскольку функциональные зависимости (4.6...4.12) однозначны и в них не включено рассеяние, то из шести переменных независи­мыми могут быть только три, например: Остальные три должны удовлетворять уравнениям связей (4.6), (4.9), (4.12), и, следовательно, полная энергия в полях связи

(4.13)

Эта энергия может быть определена, например, суммированием всех энергий (электрической и механической), подводимых к парам зажимов схемы 3 (рис. 4.3) при изменении переменных от нуля до их конечных значений:

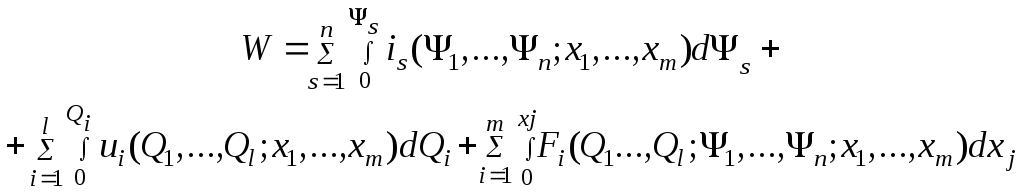
Систему переменных к их конечным значениям можно привести произвольно. Например, сначала «собрав» систему механически, поддерживая при этом и равными нулю (при этом сначала =0, а потом =0 или наоборот), установить конечные значения и. _. При этом = const, а следовательно, и послед­нее слагаемое уравнения (4.14) будет равно нулю.

Уравнения (4.7) и (4.8) могут быть решены, если и зада­ны как функции конфигурации системы, например исходя из зако­нов Фарадея и Кулона. Эти уравнения необходимо учесть во внеш­ней электрической схеме как следствие эффекта механического движения.

Для нахождения силы (рис. 4.3) используем принцип воз­можных перемещений, считая, что при изменении за время dt все остальные = 0 и эта сила электрического происхождения (связи) приложена к k-му механическому узлу. За время dt должен удовлетворяться закон сохранения энергии

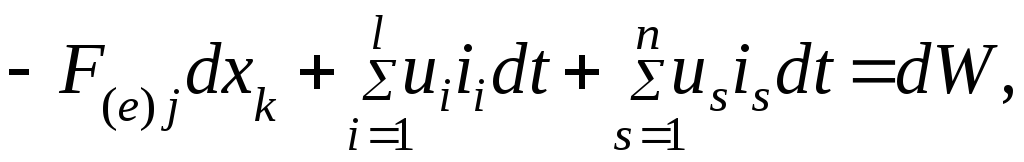(4.15)

где — энергия, поступающая на механические зажимы k-го узла (при = const); 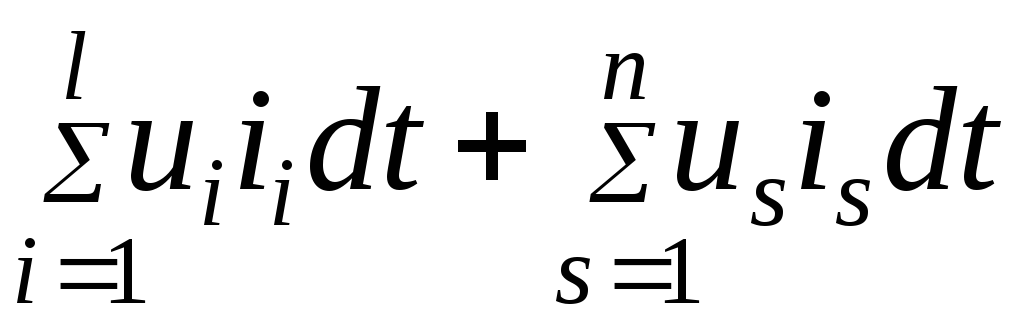— энергия, поступающая на электрические зажимы из внешней схемы.

Рассеяние не может быть учтено в полях связей. Учесть его не­обходимо во внешних электрической и механической схемах, на­пример, введением активного сопротивления.

Из уравнения (4.15) находим силу электромеханической связи:

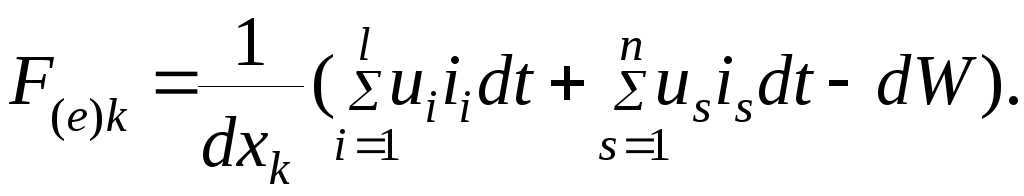(4.16)

Силу F_(e)k необходимо включить во внешнюю механическую схему 1 (рис. 4.3) и она подчиняется принципу Д'Аламбера (4 1) как одна из сил связей . Другими словами, эта сила есть действительная сила, несмотря на внешние связи, которые могут быть наложены на связанную схему от сторонних электрической и механической схем (источников).

Поскольку при определении для возможного перемещения должны удовлетворяться только внутренние связи, электрические переменные могут меняться произвольно, но в соответствии с урав­нениями (4.6) и (4.10).

Рассмотрим случай, когда механическая схема связана только с накопителями энергии магнитного поля. Тогда из (4.16) механические силы в магнитном поле

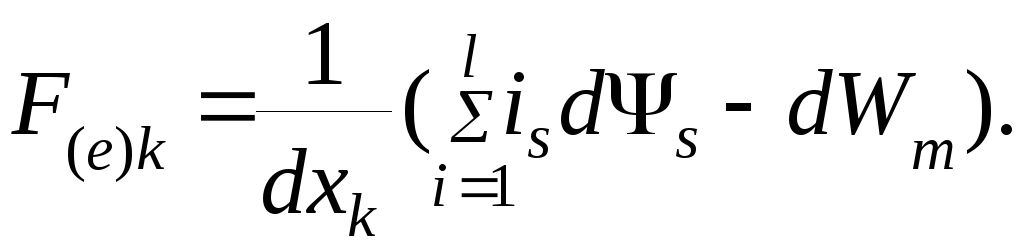(4.17)

так как

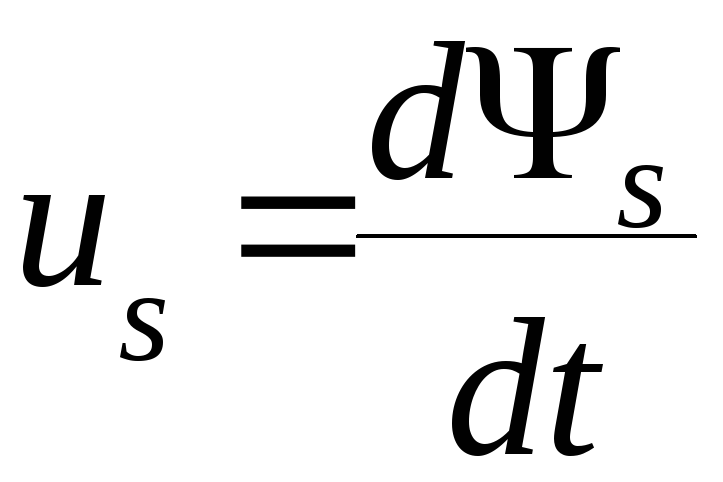
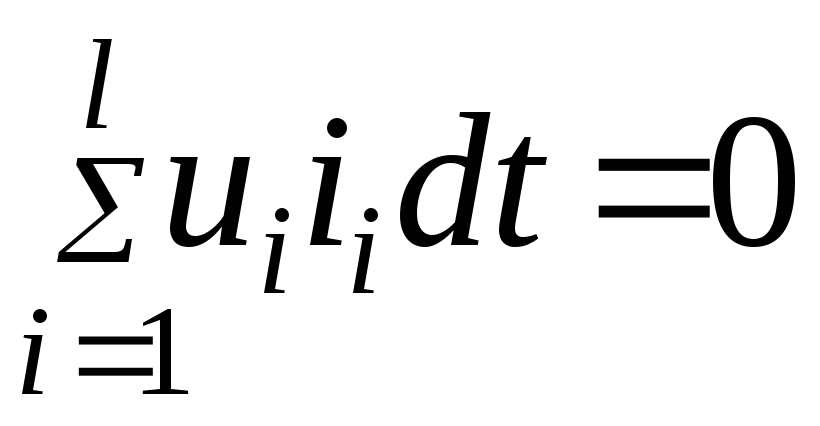и

Предположим, что имеет место возможное перемещение к-го механического узла. При этом = 0 (). Тогда при выборе в качестве независимых переменных выбираются и сле­довательно,

(4.18)

и

(4.19)

Полные дифференциалы, входящие в уравнение (4.17) ,

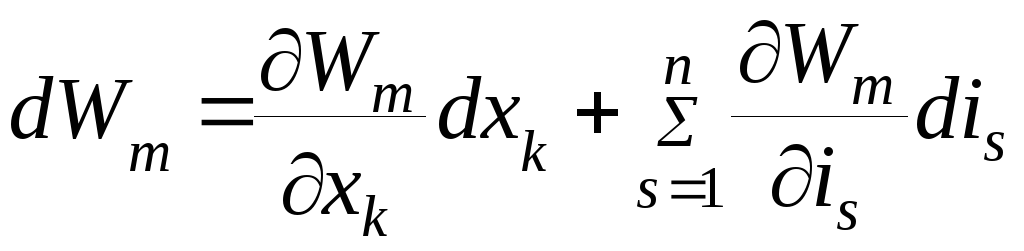(4.20)

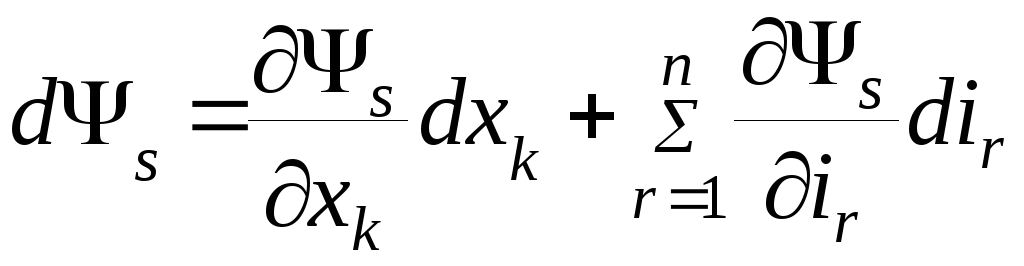(4.21)

Накопленная магнитная энергия определяется при приведении сна­чала механических, а затем электрических переменных к их конеч­ным значениям из выражения (4.14):

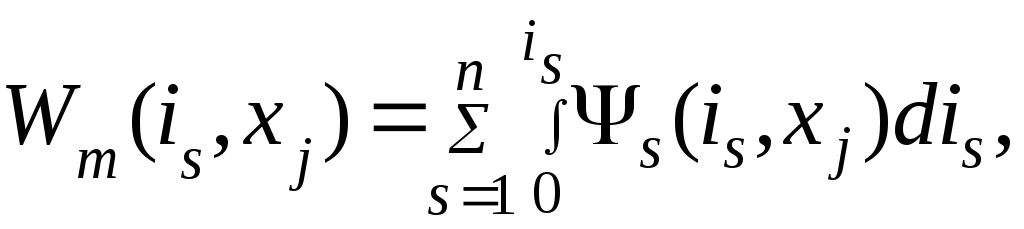(4.22)

Первый член в скобках правой части (4.17) с учетом (4.21) запишет­ся как

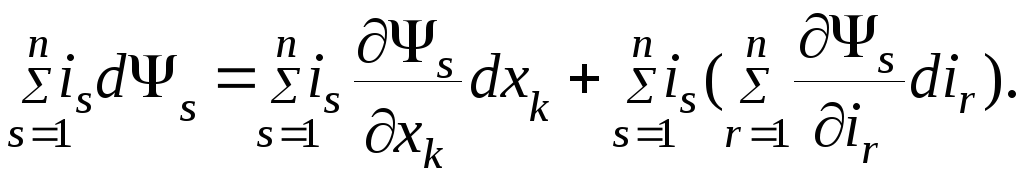(4.23)

Для нахождения силы подставим (4.20) и (4.23) в (4.17), изме­нив при этом индексы в последнем слагаемом (4.23) и сгруппиро­вав члены:

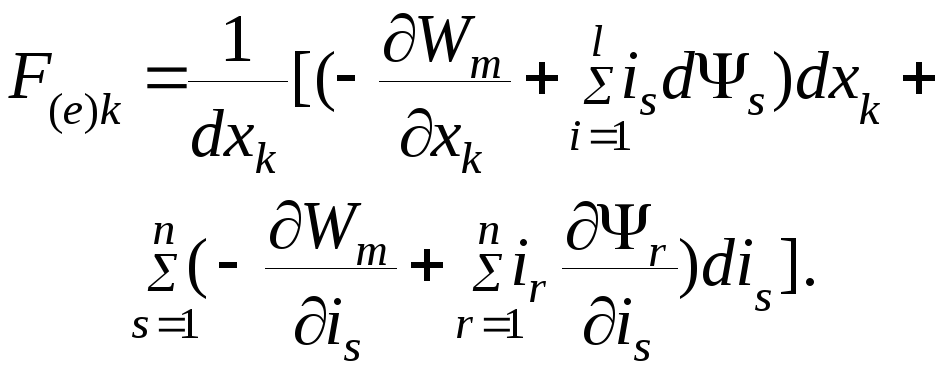(4.24)

Хотя и при возможном перемещении могут изменяться про­извольно, но сила не зависит от этих изменений, следователь­но, коэффициент при в (4.23) должен равняться нулю:

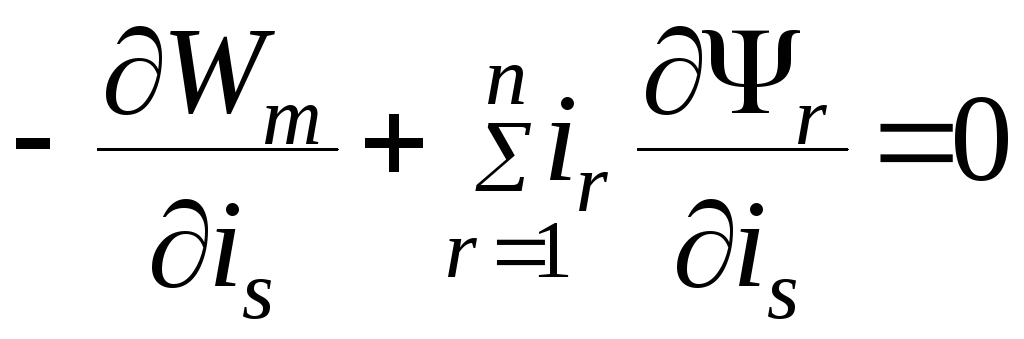(4.25)

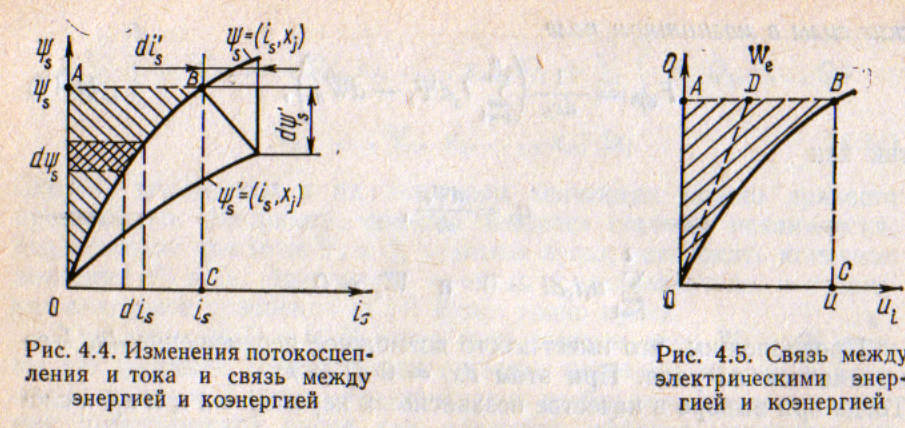
На рис. 4.4 показаны типичные зависимости потокосцепления для s-ro контура и, например, при x'_k = x_k + dx_k. Каждому приращению соответствует приращение , а также соот­ветственно . Следовательно, во-первых, уравнение (4.25) спра­ведливо, во-вторых, поскольку не зависит от то она не за­висит также и от .

Тогда из (4.24) окончательное выражение для силы

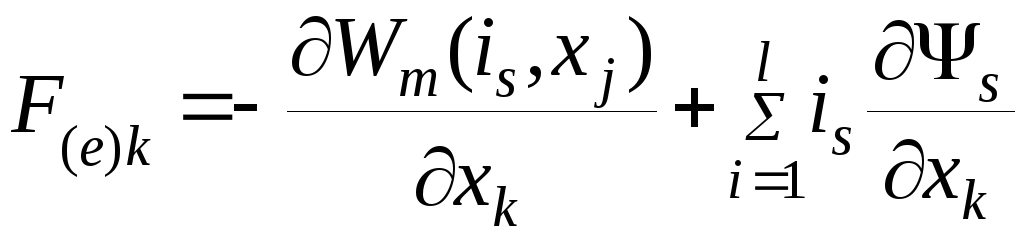(4.26)

Магнитная энергия определяется уравнением (4.22) и изобра­жена для s-го контура на рис. 4.4 площадью ОAВ. Интегрируя по частям (4.22), найдем другое выражение для магнитной энергии:

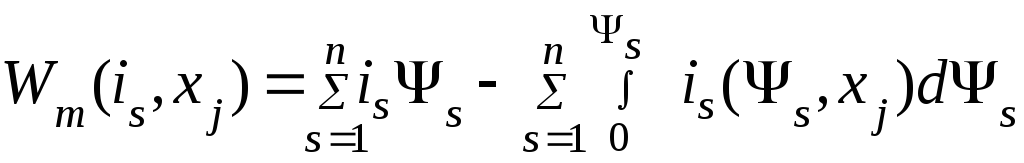(4.27)

(() (4.22)) – повтор!!!

Последнее слагаемое уравнения (4.27) представляет собой магнит­ную коэнергию , изображенную для s-го контура на рис. 4 4 площадью ОВС. Соотношения между магнитными энергией и ко­энергией из (4.27):

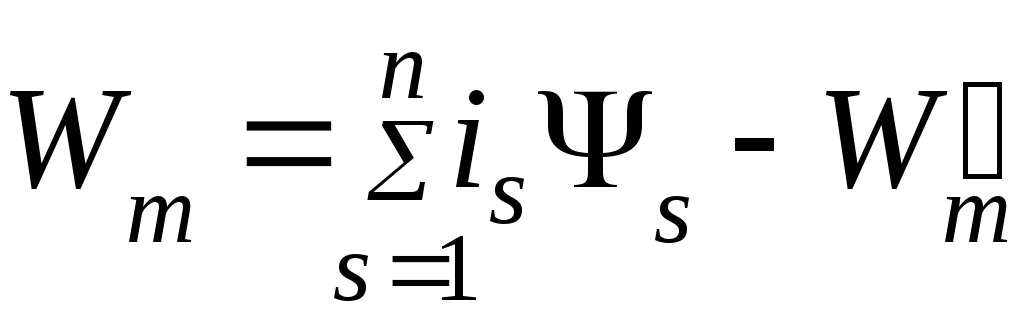(4.28)

---------------------------------------------

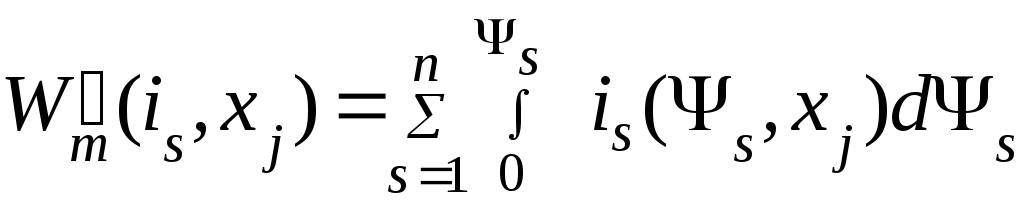– коєнергия (независимые переменные )

--------------------------------------------

Тогда сила через магнитную коэнергию выразится как

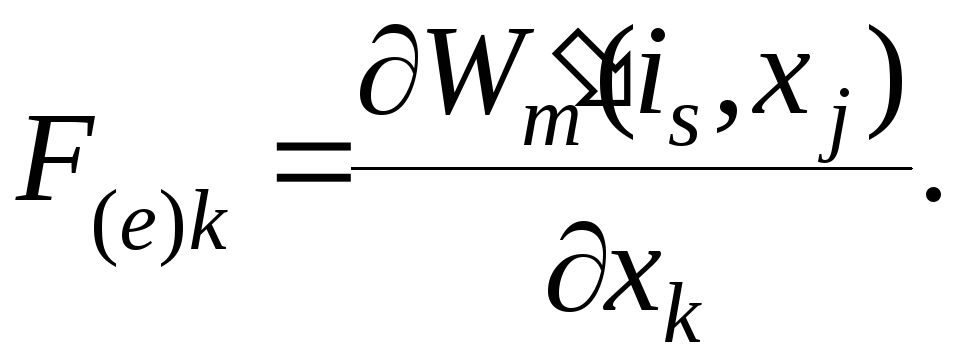(4.29)

Уравнения (4.26) и (4.29) дают силу при независимых пе­ременных и . В случае новой пары независимых переменных и и , а следовательно,

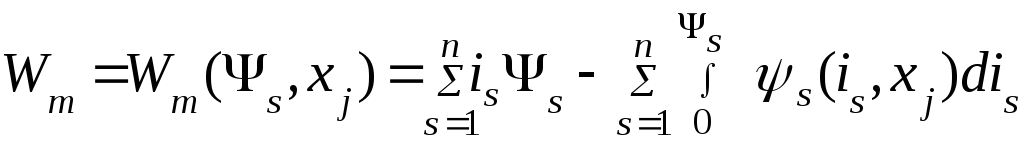
из (4.17) после аналогичных преобразований можно получить

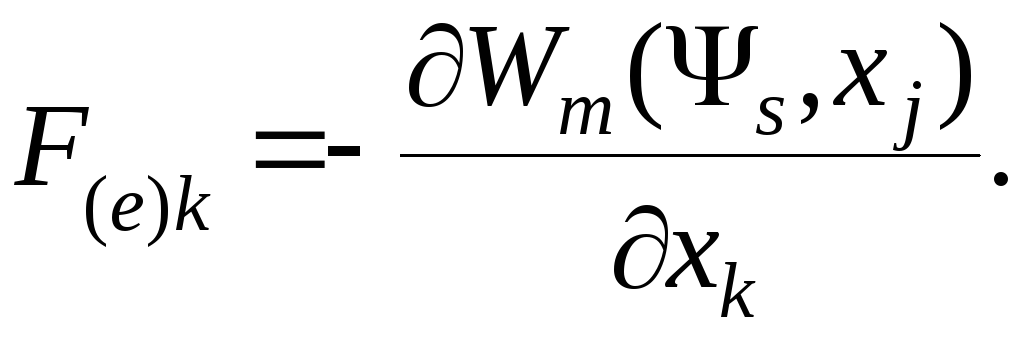(4.30)

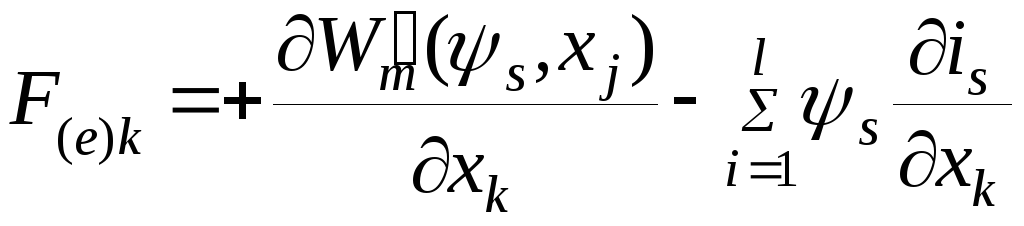(4.31)

====================================

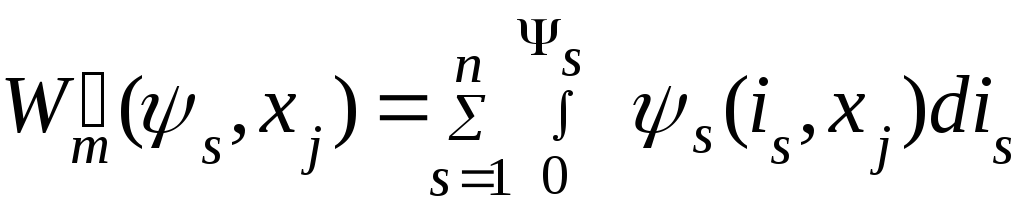– коєнергия (неззавис. перем.)

_{===================================================}

Четыре выражения (4.26), (4.29), (4.30), (4.31) для равнозначны и дают силу для данных значений ^-, и . Сила совместно с принципом Д'Аламбера и уравнениями Кирхгофа дает уравнения динамического равнове­сия, которые могут быть использованы для составления математи­ческой модели СИ, содержащих связанные преобразователи.

ПРИМЕР ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

Рассмотрим частный случай. Определения механических сил в магнитном поле для электрически линейной изме­рительной цепи.

Для электрически линейной изме­рительной цепи потокосцепления будут линейными функциями то­ков:

(4.32)

а индуктивности — однозначными функциями перемещений:

_.

Тогда после подстановки (4.32) в (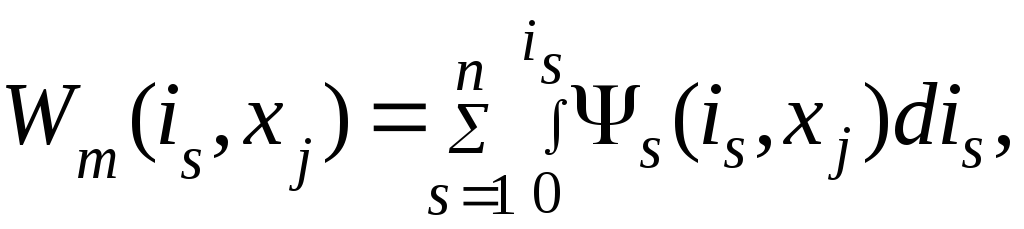4.22)

((() (4.22)))

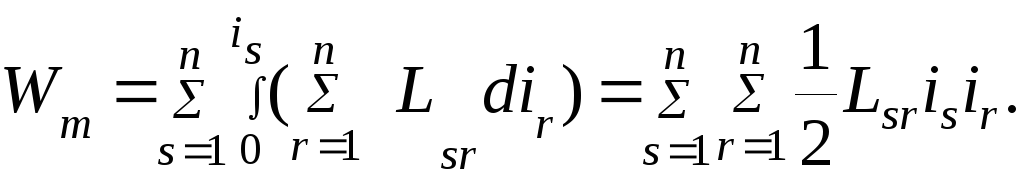. (4.33)

Из (4.28) с учетом (4.33) и (4.32) следует, что для линейных изме­рительных цепей магнитная энергия и коэнергия равны между со­бой:

Однако они должны различаться, иначе знак определяемой силы будет неверен. При независимых переменных и сила для линейной цепи через магнитную коэнергию

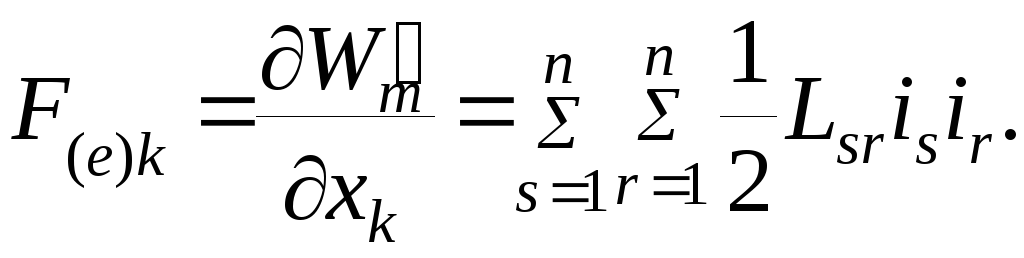(4.34)

В уравнении (4.34) сила определена в функции параметров це­пи (преобразователей) и отражает реальный процесс преобразова­ния электрической энергии в механическую в магнитных полях связи.

Аналогичный подход можно использовать для определения ме­ханических сил в электрическом поле.

Рассмотрим случай, когда ме­ханическая схема рис. 4.3 связана с накопителями энергии только электрического поля. В качестве независимых переменных выбираются и .

Из (4.16) механическая сила в электрическом поле

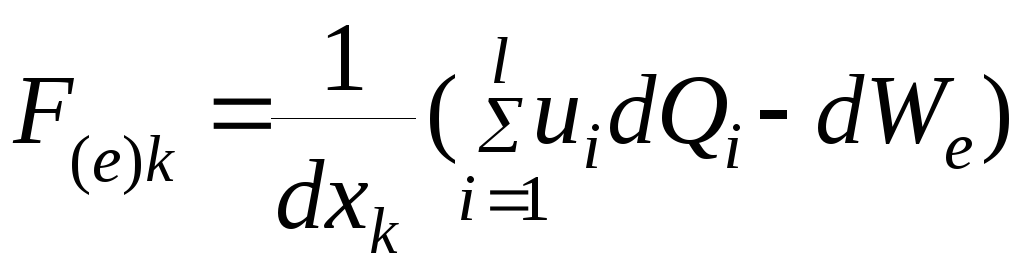(4.35)

так как

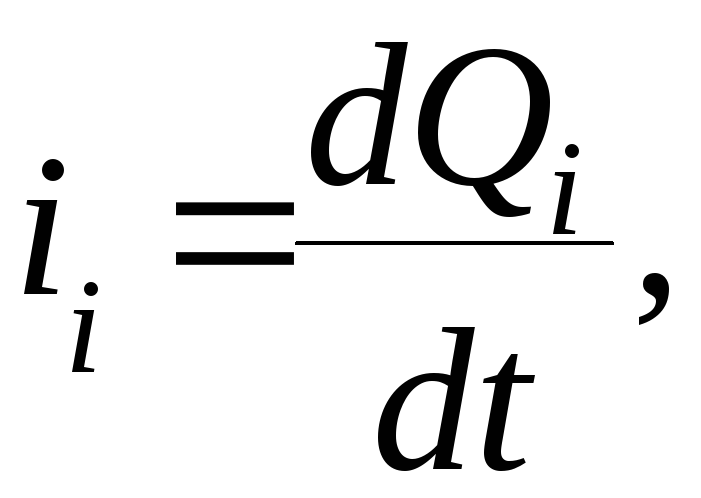
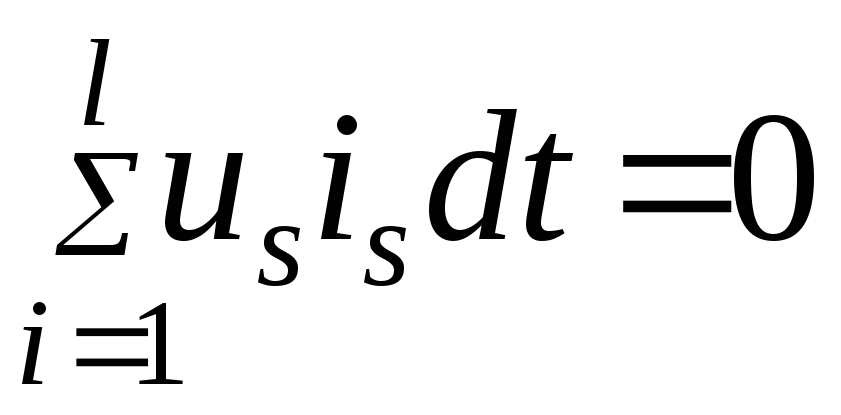и

Сила определена из условия, что возможное перемещение совместимо с внутренними связями и происходит при const и . Конечное значение запасенной энергии W_e (рис. 4.5, площадь О А В) достигается следующим образом: сначала изменяется до своих конечных значений и при этом затем механические координаты изменяются до их конечных зна­чений и при этом . Общая энергия равна сумме энергий от механического источника (площадь ODB) и от электрического ис­точника (площадь OAD).

Так как запасенная электрическая энергия является силовой функцией, то W_e может быть записана в более простой форме:

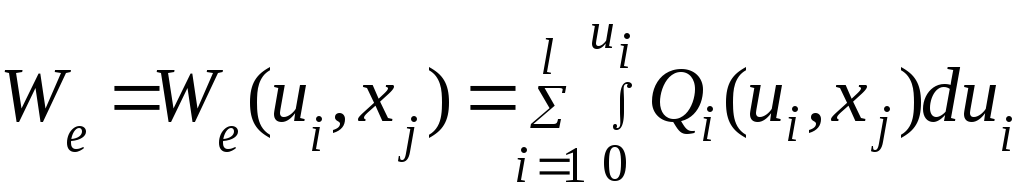(4.36)

Здесь конечное значение W_e получено для случая приведения вна­чале механической части с последующим преобразованием перемен­ных и к их конечным значениям, причем в качестве независи­мых переменных выбраны и .

Дополнив (4.36) уравнением внутренних связей (4.8) и опреде­лив полные дифференциалы, входящие в (4.35), определим силу:

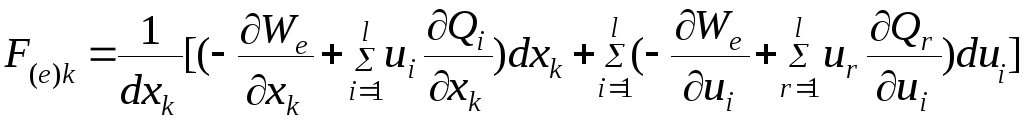_. (4.37)

Аналогично рассмотренному случаю для силы в магнитных полях связи можно показать, что коэффициент при в (4.37) равен ну­лю: .

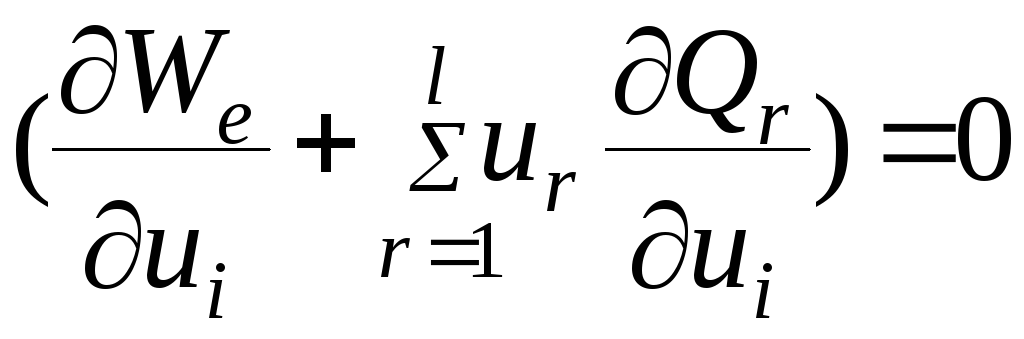Тогда окончательно выражение для силы:

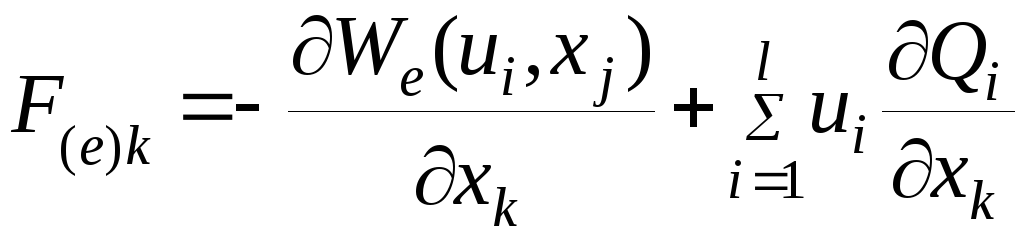(4.38)

Введем понятие электрической коэнергии (рис. 4.5), которая определяется как

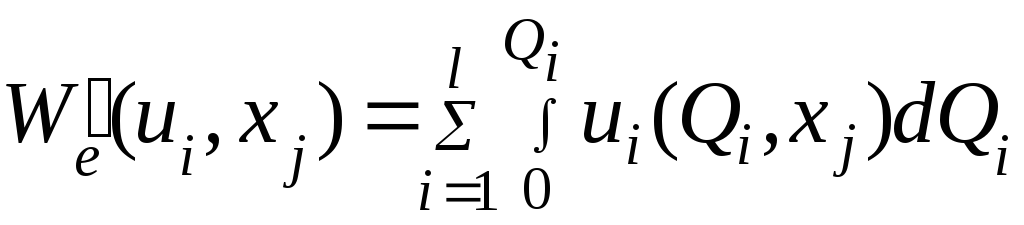(4.39)

Связь между электрическими энергией и коэнергией

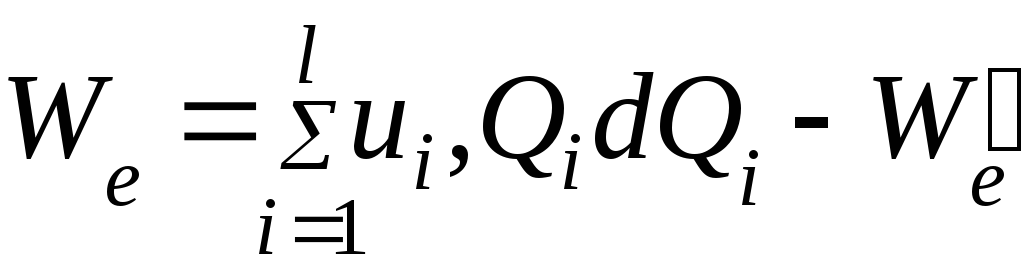(4.40)

Тогда из (4.38) после подстановки (4.40)

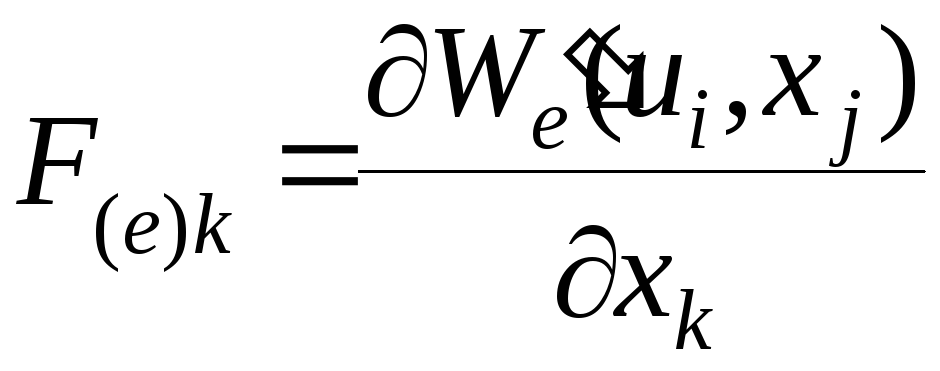(4.41)

При независимых переменных и запасенная электрическая энергия

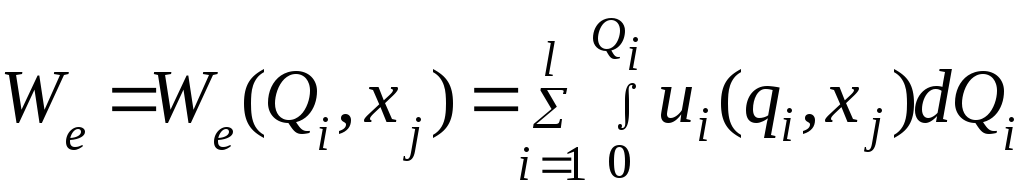(4.42)

Cила через электрическую энергию определяется из (4.35), (4.42) и (4.7) как

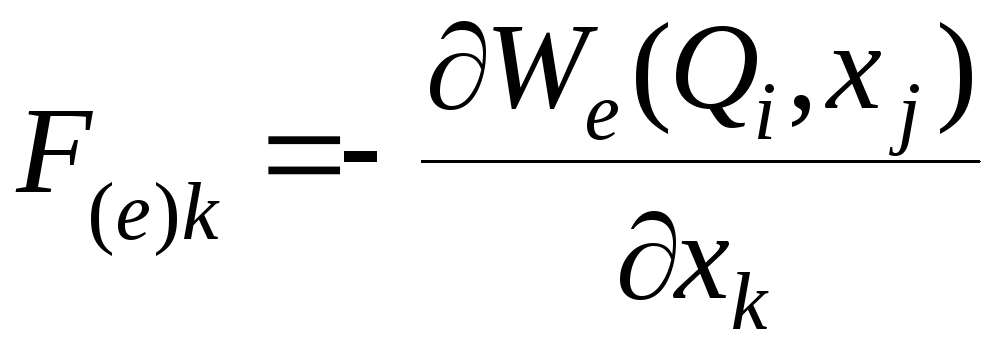(4.43)

и через электрическую коэнергию как

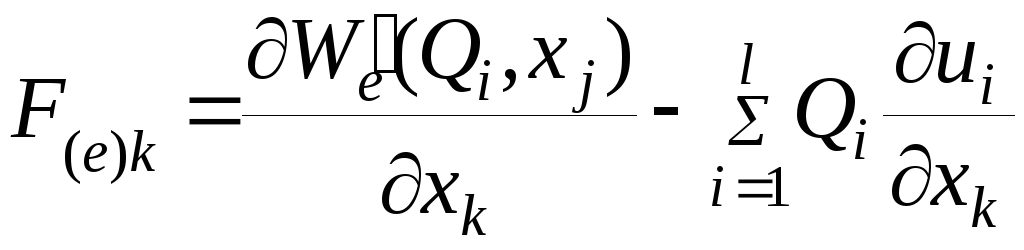(4.44)

Чтобы получить динамические уравнения, необходимо ис­пользовать совместно с принципом Д'Аламбера и уравнениями Кирхгофа.

Нами рассмотрены два частных случая, когда механическая схема соединена с накопителями энергии только магнитного или электрического полей. Если измерительная цепь с сосредоточенны­ми параметрами одновременно содержит накопители энергий маг­нитного и электрического полей, то электрические и магнитные поля могут рассматриваться раздельно, а результаты обоих рассмотре­ний объединяться с учетом внешних ограничений.