
Методичні вказівки
"Невизначений інтеграл. методи інтегрування"
для торгівельно-економічних спеціальностей
ХТЕУ КНТЕУ
професор Рабухін В.Б.
Вступ
В навчальному курсі вищої математики для торгівельно-економічних спеціальностей розділ "Невизначений інтеграл. Методи інтегрування" має важливе значення, але виявляється досить складним для засвоєння студентами. Тому ці методичні вказівки мають на меті допомагати студентам засвоїти цей розділ спрощенням роз'яснень загальних положень і вирішенням з поясненнями типових прикладів.
Дуже широке коло важливих задач з самих різних областей знань вирішується саме інтегральним численням. тому студенту потрібно навчитися методом знаходження рішень інтегралів на достигнутих прикладах.
Слід зазначити, що читачеві потрібно знати шкільну математику. Також передбачається, що студент (читач) засвоїв диференціальне числення. Бо зовсім неможливо викладати елементарні речі, майже починаючи з таблиці множення.
Операція знаходження первісної функції
Для заданого інтеграла ця операція трошки знайома студентам з шкільного курса математики. В загальному вигляді вона ab така:
∫ ƒ(x)dx=Ƒ(x)+c (1)
Тут ∫ - знак інтеграла, ƒ(x) - підінтегральна функція, dx - диференціал від незалежного аргумента х, Ƒ(x) - первісна ( чи першообразна) функція, С - невизначена стала величина. таке співвідношення (1) підпорядковується завжди головному правилу: похідна від первісної функції дорівнює підінтегральної функції ƒ(x). Яким би складним не був інтеграл, він вирішен вірно, якщо при диференціюванні отриманого рішення получаємо підінтегральну функцію. Тобто
[Ƒ(x)+c]'ₓ=ƒ(x) [Ƒ(x)]'ₓ=ƒ(x) (2)
невизначена стала при дифернціюванні дає О, тому вона може бути будь-якою. Саме тому її називають невизначеною. Це означає, що одній підінтегральній функції відповідає ціле сімейство первісних функцій, які відрізняються між собою тільки сталою величиною.
Слід
зазначити, що визначений інтеграл
 ,
який має верхню та нижню межі а і b,
дає при розвязанні
якесь конкретне значення, чи число.
Прямим слідством співвідношення (2) і
того, що невизначене інтегрування є
оберненим процесом відносно диференціювання,
являється основні правила інтегрування.
Так саме, як і невизначені інтеграли
від ряда функцій, чи так звані табличні
інтеграли.
,
який має верхню та нижню межі а і b,
дає при розвязанні
якесь конкретне значення, чи число.
Прямим слідством співвідношення (2) і
того, що невизначене інтегрування є
оберненим процесом відносно диференціювання,
являється основні правила інтегрування.
Так саме, як і невизначені інтеграли
від ряда функцій, чи так звані табличні
інтеграли.
Загальні правила інтегрування
-
Інтеграл від суми функцій дорівнює сумі інтегралів від кожної з функцій
∫[ƒ(x)+φ(x)]dx=∫ƒ(x)dx+∫φ(x)dx(3)
Це тому, що похідна від суми функцій дорівнює сумі похідних від кожної з функцій.
[F1(x)+F2(x)]'x=[F1+(x)]'x+[F2(x)]'x=ƒ(x)+φ(x)
Невизначені сталі при диференціюванні дають нуль.
-
Сталу величину можна виносити (чи вносити) з під знака інтеграла
∫λƒ(x)=λ∫ƒ(x)dx (4)
Це теж наслідок властивостей диференціювання.
-
Інтеграл від сталої величини дорівнює її добутку на незалежну перемінну
∫λdx=λx+c (5)
Тому, що [λx+c]'x=λ
Розглянемо тепер інтегрування деяких основних функцій, чи табличні інтеграли. Треба розуміти, що підбір тут умовний, але беруться ті формули, які найбільш часто застосовуються.
Табличні інтеграли
-
Розглянемо спочатку інтегрування степеневої функції
y=xn, n≠-1 (цей виняток ми пояснимо далі)
∫ xndx= +c
тому, що [
+c
тому, що [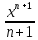 +c]'x=xn
+c]'x=xn
-
∫
 =lnx+c
(це степенева функція y=xn
при n=-1)
тому, що [lnx+c'x=
=lnx+c
(це степенева функція y=xn
при n=-1)
тому, що [lnx+c'x= =x-1
=x-1 -
∫x0dx=∫dx=x+c ,бо (x+c)'x=1
Тобто інтеграл та диференціал взаємно знищують один одного.
-
Далі показникова функція y=ax
∫axdx= +c,
бо [
+c,
бо [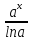 +c]=
+c]= *lna=ax
*lna=ax
-
Особливий випадок показникової функції - це є елемента y=ex
∫exdx=ex+c, бо lne=1
Далі розглянемо інтеграли від тригонометричних та обернено тригонометричних функцій.
-
∫sinxdx=-cosx+c, бо [-cosx+c]'x=sinx
-
∫cosxdx=sinx+c, бо [sinx+c]'x=cosx
-
∫tgxdx=∫
 dx=-∫
dx=-∫ =-|cosx|+c
=-|cosx|+c
Диференціювання дає підінтегралбну функцію tg x, бо це диференціювання складної функції
[-ln|cosx|+c]'x=- =tgx
=tgx
-
Так само буде і для функції y=ctgx
∫ctgxdx=∫ dx=∫
dx=∫ =ln|sinx|+c
=ln|sinx|+c
Диференціювання
для перевірки рішень [ln|sinx|+c]'x= (sinx)'x=ctgx
(sinx)'x=ctgx
-
∫
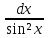 =tgx+c,
бо [tgx+c]'x=
=tgx+c,
бо [tgx+c]'x=
-
∫
 =-ctgx+c,
бо [-ctgx+c]'x=
=-ctgx+c,
бо [-ctgx+c]'x=
-
∫
 =arcsinx+c,
бо [arcsinx+c]'x=
=arcsinx+c,
бо [arcsinx+c]'x=
Якщо цю формулу трошечки ускладнити, то відповідь буде: а - стала величина
∫ =
= ∫
∫ =arcsin
=arcsin +c
+c
-
∫
 =arctgx+c,
бо
[arctgx+c]'x=
=arctgx+c,
бо
[arctgx+c]'x=
Невеличке узагальнення цієї формули легко вирішується:
∫ =
= ∫
∫ =
= ∫
∫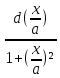 =
= arctg
arctg +c
+c
До цього списку табличних інтегралів додамо ще дві формули, які доводиться досить часто використовувати
-
∫
 =
=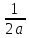 ln|
ln|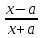 |+c Звідки
це береться?
|+c Звідки
це береться?
Це легко показати, а саме
∫ =
= ∫
∫ dx=
dx= ∫
∫ dx=
далі ділемо почленно =
dx=
далі ділемо почленно = ∫
∫ dx-
dx- ∫
∫ dx=
тепер
скорочуємо і отримаємо два інтеграли,
які легко до ....... =
dx=
тепер
скорочуємо і отримаємо два інтеграли,
які легко до ....... =
 ∫
∫ -
- ln|x-a|-
ln|x-a|- |x+a|+c=
|x+a|+c= ln|
ln| |+c.
си отримаєм те, що нам потрібно
|+c.
си отримаєм те, що нам потрібно
-
{ln|x+
 |+c}'x=
|+c}'x= *(x+
*(x+ )'x=
)'x= *(1+
*(1+ (x2+a)-½*2x)=
=
(x2+a)-½*2x)=
= (1+
(1+ )=
)= *
* =
= Перевірка
показала, що формула 15 дійсно правильна
Перевірка
показала, що формула 15 дійсно правильна
Таким чином ми маємо 15 табличних інтегралів. До них можна було б додати ще декілька формул, але ми обмежмося цими п'ятнадцять.
Розглянемо на прикладах, яким чином застосовувати ці табличні інтеграл. Почнемо з степеневої функції.
Приклад
1.
∫ dx=∫x½dx=
dx=∫x½dx= +c=
+c= +c
+c
Приклад
2.
∫ =∫
=∫ dx=
dx= +c=-
+c=- +c
+c
Приклад
3.
∫3,4 dx=
dx= +c
+c
Приклад
4.
∫ =
= ∫
∫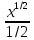 +c=
+c= +c
+c
Приклад
5.
∫ dx=
dx= +c
+c
Приклад
6.
∫ dx=∫
dx=∫ dx=
dx= +c=
+c= +c
+c
Тепер розберемо рішення трошки складніших інтегралів.
Приклад
7. ∫( +1)(x-
+1)(x- +1)dx=∫(x
+1)dx=∫(x -x+
-x+ +x-
+x- -1)dx=∫x
-1)dx=∫x dx-∫dx=
dx-∫dx=
= -x+c=
-x+c= -x+c
-x+c
Приклад
8.
∫ dx=∫
dx=∫ dx-∫
dx-∫ dx+∫
dx+∫ =
= -lnx+c
-lnx+c
Приклад
9. ∫( dz=∫
dz=∫ dz=∫
dz=∫ dz-2∫
dz-2∫ +∫dz=-
+∫dz=- -2lnz+z+c
-2lnz+z+c
Приклад
10.
∫ dx=∫3dx-2∫(1,5
dx=∫3dx-2∫(1,5 dx=3x-2
dx=3x-2 +c
+c
До цих всіх прикладів додамо ще декілька тригонометричних прикладів.
Приклад
11. ∫ dx=∫
dx=∫ dx=
dx= ∫
∫ =
= ∫dx=
∫dx= tgx+
tgx+ x+c
x+c
Приклад
12.
∫ dx=∫
dx=∫ dx=∫
dx=∫ dx=
dx=
=∫ dx=∫
dx=∫ -∫
-∫ =-ctgx-tgx+c
=-ctgx-tgx+c
Приклад
13. ∫ xdx=∫
xdx=∫ dx=∫
dx=∫ dx=∫
dx=∫ -∫dx=tgx-x+c
-∫dx=tgx-x+c
Приклад
14. ∫ dx=∫(1-cosx)dx=x-sinx+c
dx=∫(1-cosx)dx=x-sinx+c
Приклад
15. ∫ dx=∫
dx=∫ +∫
+∫ =∫
=∫ +∫
+∫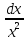 =arctgx-
=arctgx- +c
+c
Приклад
16. ∫ dx=∫
dx=∫ =∫
=∫ +∫
+∫ =∫
=∫ +2∫
+2∫ =
=
=ln|x|+2arctgx+c
Приклад
17. ∫ =Враховуючи,
що cos2x=cos2x-
=Враховуючи,
що cos2x=cos2x- ,
маємо
,
маємо
=∫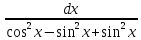 =∫
=∫ =tgx+c
=tgx+c
Всі ці приклади на пряме, чи майже пряме, застосування табличних інтегралів. Якщо так просто не получається, то можна прибігти до таких перетворень, які потім дадуть можливість застосувати табличні інтеграли. Такі перетворення і є методом інтегрування. Тепер на вже можна перейти до деяких, найбільш часто застосованих методів інтегрування.
В чому полягає головна ідея застосування всіх цих методів. Всі вони, як правило, дають змогу спростити інтеграл і спростити його до табличних, рішення яких ми вже маємо.
