Лабораторная работа № 14

Тема: «Создание меню. Массив указателей на функции»

1. Цель работы

   1. Получение навыков в написании программ с использованием массива указателей на функции.

   2. Научиться составлять программу определения корня трансцендентного уравнения с заданной точностью различными методоми.

   3. Получение навыков написания программы с использованием меню.

2. Техническое обеспечение

   1. Персональная ЭВМ IBM PC/286 и более поздних моделей.

   2. Клавиатура.

   3. Дисплей.

   4. Печатающее устройство.

3. Программное обеспечение

1. Операционная система Windows

2. Система программирования Visual C++ версия 6.0 или Borland C++ версия 3.1 и более поздние версии.

4. Постановка задачи

Найти корень уравнения, указанного в конкретном варианте, используя метод деления отрезка, метод хорд и метод Ньютона (касательных). Значение корня считать с погрешностью . Сделать оценку сходимости для каждого из указанных выше методов, т. е. определить количество итераций при вычислении корня указанными выше методами.

5. Содержание отчета

5.1. Тема и цель работы.

5.2. Схема алгоритма решения задачи.

5.3. Текст программы.

5.4. Результаты выполнения программы.

Общие сведения

Решение уравнения методом деления отрезка пополам (бисекций)

Существуют различные методы решения уравнения f(x) = 0. Из простых методов назовем метод Ньютона, метод хорд и метод деления пополам. Последние два метода характеризуются медленной сходимостью, но реализация их проста.

Для этих двух методов существенно, чтобы функция была непрерывна и ограничена в заданном интервале [a, b], внутри которого ищется корень. Предполагается также, что f(a) и f(b) имеют разные знаки.

Рассмотрим подробнее один из этих методов, а именно метод деления пополам, так как по сравнению с методом хорд данный метод характеризуется большей сходимостью. Этот метод состоит в выполнении итераций, начиная с отрезка [a, b] на оси абсцисс на котором функция меняет знак, т.е. имеется точка пересечения графика функции с осью х (рисунок 1).

При заданной точности  метод состоит из таких шагов:

1. Вычислить f(a) и f(b).

2. Положить c = (a + b)/2 и вычислить f(с).

3. Если f(с) = 0, то принять в качестве решения значение с, вывести его и прекратить вычисления, иначе перейти к шагу 4.

4. Если f(c) и f(a) имеют одинаковые знаки, то заменить a на c.

5. Если f(c) и f(b) имеют одинаковые знаки, то заменить b на c.

6. Если |b  a|   ( - заданная погрешность вычислений), то принять в качестве решения последнее значение с, вывести его и прекратить вычисления, в противном случае перейти к шагу 2.

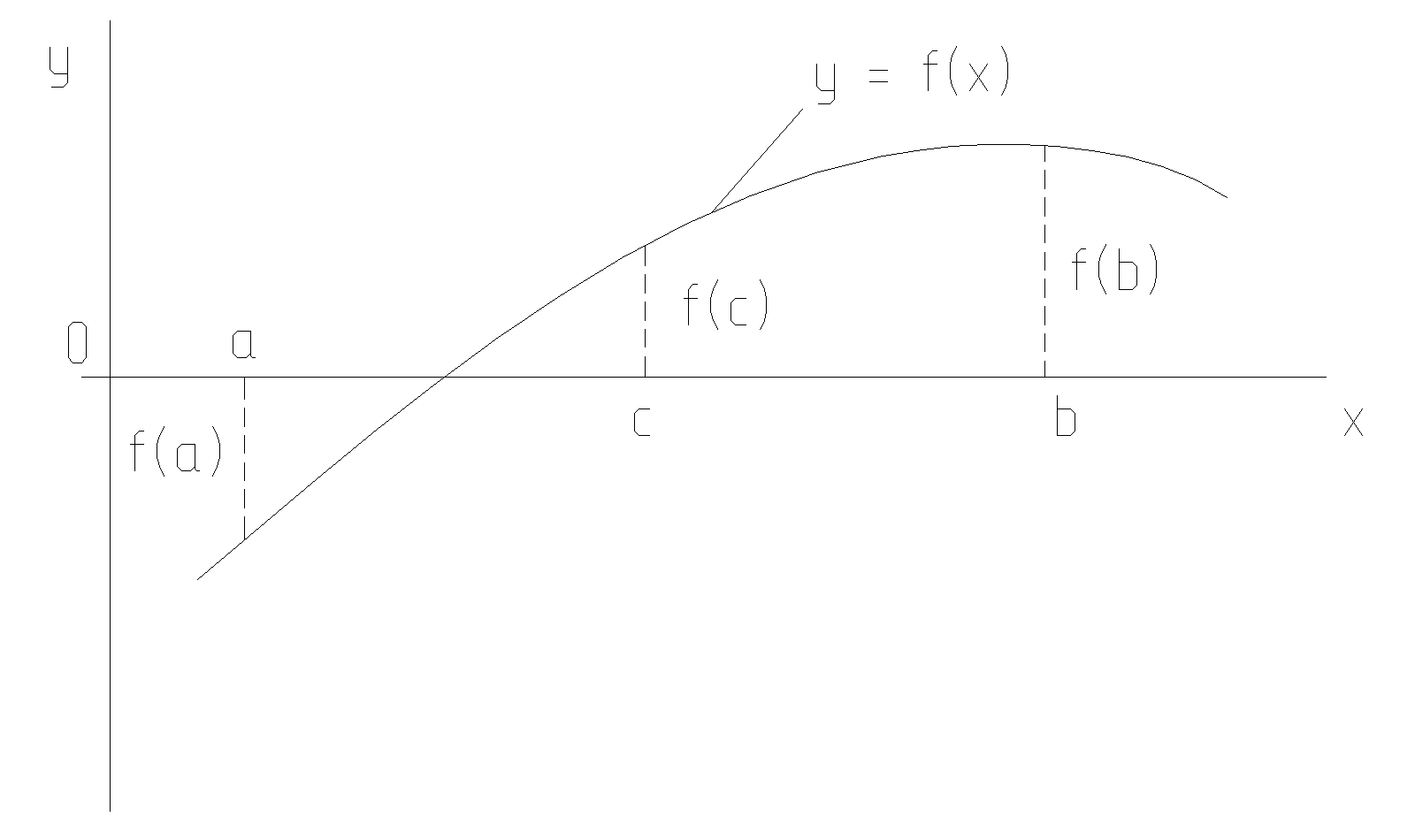
Для определения значения конца отрезка b, на котором функция меняет знак, при заданном значении начала отрезка а используют следующий итерационный алгоритм:

1. Задают начальное значение х = a + h. Здесь h – это заданный шаг изменения х.

2. Вычислить значения f(a) и f(x).

Если f(a) иf(x) имеют разные знаки, то принятьb=xи прекратить вычисления, иначе принятьx=x +hи перейти к шагу 2.

Решение нелинейного уравнения методом хорд

Рассматриваемый метод так же, как и метод деления отрезка пополам, предназначен для уточнения корня на интервале [a, b], на концах которого левая часть уравнения f(x) = 0 принимает разные знаки. Значение начала интервала а вводится с клавиатуры.

Очередное приближение теперь в отличие от метода деления отрезка пополам берем не в середине отрезка, а в точке х₁, где пересекает ось абсцисс прямая линия, проведенная через точкиf(a)иf(b)(рисунок 1).

В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a,x₁] или [x₁,b], на концах которого функцияf(x)принимает значения с разными знаками.

Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности 

|x_n – x_n-1| < 

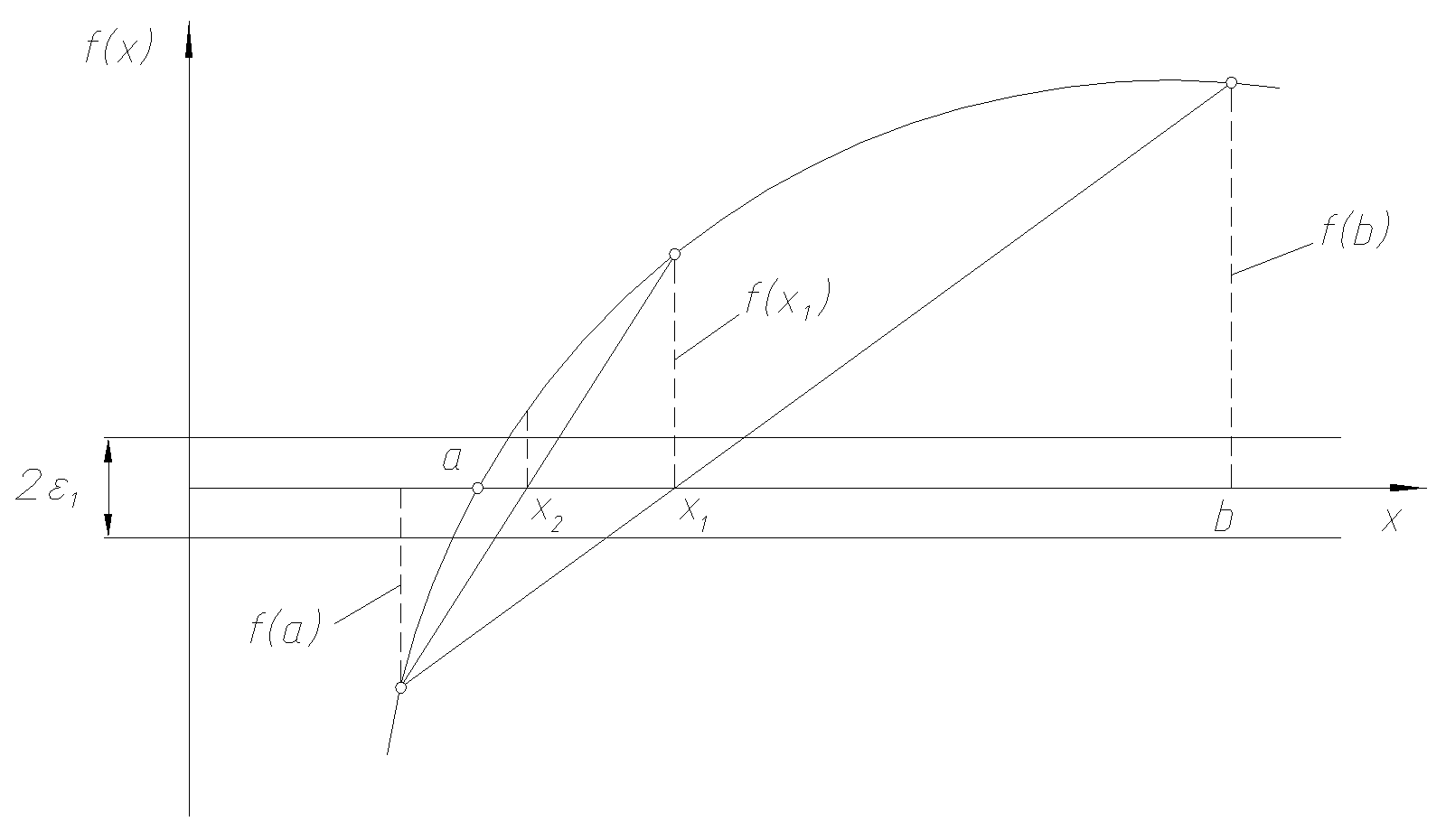
Рисунок 1 – Метод хорд

Уравнение прямой линии, проходящей через точки f_a = f(a) и f_b = f(b), запишем в общем виде

y(x) = kx + c .

Коэффициенты k и c уравнения этой прямой определим из условий

f_a = ka + c ,

f_b = kb + c .

Вычитая левые и правые части последних соотношений, получим

, c = f_a – ka .

Точку пересечения прямой y(x) с осью абсцисс получим, приравнивая y(x) нулю

(1)

или

. (2)

Метод Ньютона (метод касательных)

Рассмотрим графическую иллюстрацию метода (рисунок 1). Предположим, каким-либо методом определено начальное приближение к корню. В точке x₀ вычислим левую часть решаемого уравненияf₀=f (x₀), а также производную в этой точкеf (x₀) =tg . Следующее приближение к корню найдем в точкеx₁, где касательная к функцииf(x), проведенная из точки (x₀,f₀) пересекает ось абсцисс. Затем считаем точкух₁в качестве начальной и продолжаем итерационный процесс. Из рисунка 1 видно, что таким способом можно приближаться к корнюх*. При этом расстояние между очереднымx_k+1и предыдущимx_kприближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

|x_k+1–x_k| <,

где - допустимая погрешность вычисления корня.

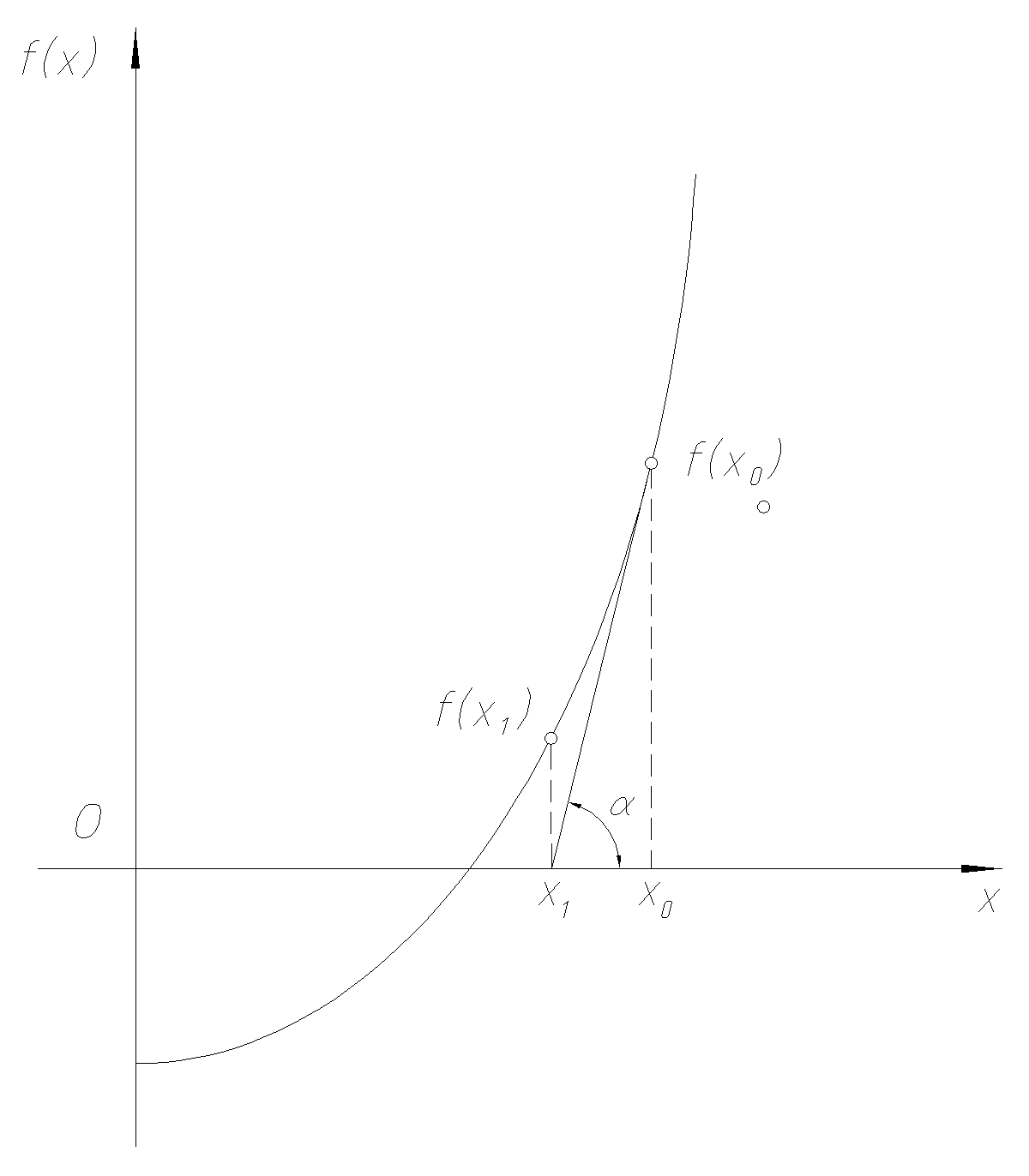
Рисунок 1 – Метод Ньютона

Из геометрических соотношений рисунка 1 получим основную формулу метода Ньютона

x₁=x₀–f(x₀) /f(x₀) .

В общем виде для k-го шага итерационного процесса последнее соотношение принимает вид

x_k+1=x_k –f(x_k) /f(x_k) .

Массивы указателей на функцию

В некоторых типах программ пользователь может выбирать некоторый вариант из списка возможных действий. Например, в системе подсчета может быть меню более с 20 вариантами. Когда выбор сделан, программа выполняет соответствующую функцию. Это может быть сделано двумя способами. Во первых, для этого можно использовать оператор switch, например

void menu(void)

{

char ch;

printf(“1. Проверка орфографии\n”);

printf(“2. Корректировка ошибок\n”);

printf(“3. Вывод ошибок на экран\n”);

printf(“Сделайте ваш выбор: “);

do{

ch=getche(); /* Чтение клавиатуры */

switch (ch) {

case ‘1’:

check_spelling();

break;

case ‘2’:

correct_errors();

break;

case ‘3’:

display_errors();

break;

}

} while (ch != ‘1’ && ch != ‘2’ && ch != ‘3’);

}

В приложениях, где требуется высокая производительность, лучше применять другой способ. Можно использовать массив указателей, содержащих адреса функций. Выбор, сделанный пользователем, декодируется и используется для индексации массива указателей, вызывая выполнение необходимой функции. Этот метод гораздо быстрее, чем метод использования оператора switch.

Для того, чтобы понять, как можно использовать массив указателей на функции для построения меню, преобразуем предыдущий пример. Если функции, выполняющие действия по проверке орфографии называются check_spelling(),correct_errors(),display_errors(),quit(), то следующий фрагмент программы корректно инициализирует массив указателей на функции:

void check_spelling (void), correct_errors (void), display_errors (void), quit (void);

int menu (void);

void (*options[ ]) (void) = {

check_spelling,

correct_errors,

display_errors,

quit

} ;

Необходимо обратить особое внимание на способ объявления массива указателей на функции, а также на использование круглых и квадратных скобок.

Хотя эта программа не выполняет никаких действий по проверке орфографии, она демонстрирует правильный способ выполнения функций с помощью указателей на функции. Следует обратить внимание, как функция menu()автоматически возвращает правильный индекс в массив указателя:

#include <stdio.h>

#include <stdlib.h>

#include <conio.h>

#include <string.h>

void check_spelling (void), correct_errors (void), display_errors (void), quit (void);

int menu (void);

void (*options []) (void) = {

check_spelling,

correct_errors,

display_errors,

quit

} ;

int main(void)

{

inti;

i=menu() ; /* получение выбора пользователя *.

(*options [i]) ( ) ; /* выполнение */

return 0;

}

int menu (void)

{

char ch;

do {

printf(“1. Проверка орфографии\n”);

printf(“2. Корректировка ошибок\n”);

printf(“3. Вывод ошибок на экран\n”);

printf(“4. В ы х о д\n”);

printf(“Сделайте ваш выбор: “);

ch = getche();

printf(“\n”);

} while (!strchr (“1234”, ch));

returnch– 49; /* преобразование к целочисленному эквиваленту */

}

void check_spelling (void)

{

printf(“In check_spelling”);

}

void correct_errors (void)

{

printf(“In correct_errors”);

}

void display_errors (void)

{

printf(“In display_errors”);

}

void quit (void)

{

printf(“In quit”);

exit(0);

}

Программа работает следующим образом. Сначала на экран выводится меню и пользователь вводит число, соответствующее его выбору. Поскольку введенное число представлено в ASCII-коде, то необходимо вычесть 49 (ASCII-код цифры 0) для получения двоичного числа. Данное значение затем возвращается вmain ()и используется как индекс массиваoptions– массива указателей на функцию. После этого вызывается соответствующая функция. Строковая функцияstrchr(“1234”,ch) возвращает указатель на первое вхождение символаchв строку “1234”.

6. Методические указания

7.1 Вычисление корня уравнения каждым из указанных выше методов оформить в виде функции, в которой вычислить количество итераций (повторений цикла).

7.3 Для выбора метода вычисления корня уравнения использовать меню, разработанное с применением массива указателей на функции.

7.4 За начальное приближение x₀принять найденное значение конца отрезкаb, на котором заданная функцияf (x) меняет знак. Алгоритм определения этого значения приведен в методических указанияx

Варианты заданий

1) Найти корень уравнения

e^x – 2x– 10 = 0

с точностью = 10^-4при заданном значении начала отрезкаа= 0.

2) Найти корень уравнения

0.1e^x–sin²x+ 0.5 = 0

с точностью e= 10^-4при заданном значении начала отрезкаа=5.

3) Найти корень уравнения

с точностью e= 10^-4при заданном значении начала отрезкаа=-2.

4) Найти корень уравнения

e^0.724x+0.3– 2.831 = 0

с точностью e= 10^-4при заданном значении начала отрезкаа= 0.

5) Найти корень уравнения

x+ 0.5sin x+ 1 =0

с точностью e= 10^-4при заданном значении начала отрезкаа=-1.

6) Найти корень уравнения

x–cosx= 0

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

7) Найти корень уравнения

1.4^x–x= 0

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

8) Найти корень уравнения

0.5x–ln|x| = 0

с точностью e= 10^-5при заданном значении начала отрезкаа=-1.

9) Найти корень уравнения

x³+sin x– 3.5x+ 1 = 0

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

10) Найти корень уравнения

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

11) Найти корень уравнения

(4 + x²)(e^x–e^-x) = 18

с точностью e= 10^-5при заданном значении начала отрезкаа= 1.

12) Найти корень уравнения

3x²–cos2x= 1

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

13) Найти корень уравнения

с точностью e= 10^-4при заданном значении начала отрезкаа= 0.

14) Найти корень уравнения

с точностью e= 10^-5при заданном значении начала отрезкаа= 0.

15) Найти корень уравнения

с точностью e= 10^-4при заданном значении начала отрезкаа= 1.