Задание 1 по теме “Матрицы и действия над ними. Обратная матрица”.

Матрицей = () размера mn называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:

Операция сложения имеет место только для матриц одинаковых размеров.

Суммой ( разностью) двух матриц и служит матрица , для которой и обозначается .

Произведением матрицы на число  называется матрица , для которой .

Матрицу будем называть согласованной с матрицей , если число столбцов матрицы равно числу строк матрицы .

Произведением матрицы размера mr на матрицу размера rn называется матрица размера mn с элементами

(поэлементное умножение i-й строки матрицы на k-й столбец матрицы В). B общем случае .

Матрица с элементами называется единичной матрицей n-го порядка.

Матрица называется обратной к матрице , если .

Элементы обратной матрицы вычисляются по формулам , где -алгебраическое дополнение элемента матрицы А, а – ее определитель.

Пример 1. Даны две матрицы и. Найти: а); б); в); г) ; д) .

Решение.

в) Вычислим определитель матрицы

.

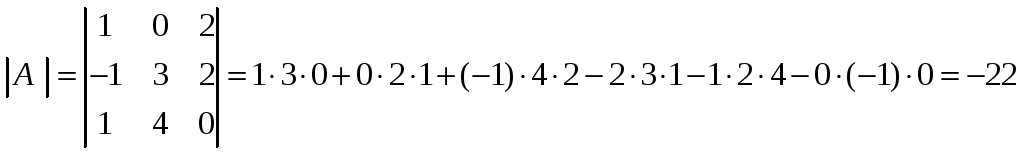Так как , то обратная матрица существует

.

Найдём алгебраические дополнения элементов матрицы:

Таким образом,

.

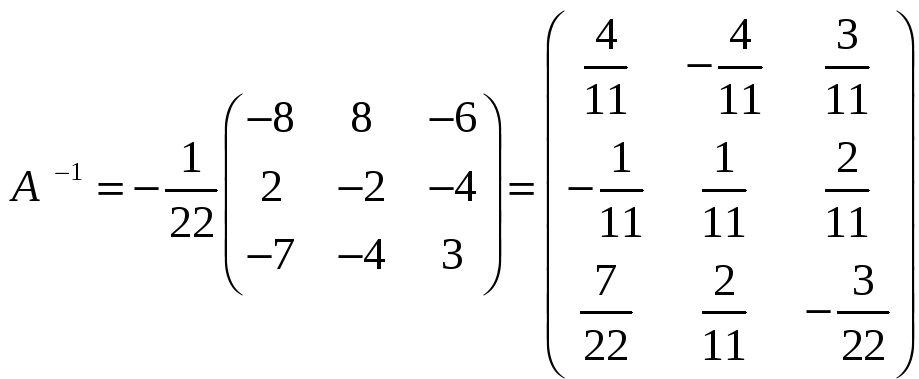г)

д)

ЗАДАНИЕ 2 по теме “Решение систем линейных уравнений”.

Система трёх линейных уравнений с тремя неизвестными имеет вид

где - коэффициенты системы; - свободные члены. Определитель третьего порядка , составленный из коэффициентов при неизвестных, называется определителем системы. Если , то единственное решение системы выражается формулами Крамера:

где - определители третьего порядка, получаемые из определителя системы заменой 1, 2 или 3-го столбца соответственно свободными членами .

Определителем второго порядка называется число, равное , т.е. .

Определителем третьего порядка называется число, которое вычисляется по правилу

Систему можно записать в матричной форме:, где

Тогда её решение имеет вид , если определитель системы отличен от нуля.

Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т.е. r < n , то система имеет бесконечное множество решений. Свободные n – r неизвестных выбираются произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.

Пример 2. Проверить совместность системы уравнений и в случае совместности решить её: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.

Решение. Вычислим определитель системы:

Так как , то система совместна.

а) Найдём решение по формулам Крамера. Для этого найдём :

Подставляя найденные значения определителей в формулы Крамера, получаем искомое решение системы :

б) Решим матричным методом. Для этого введём обозначения:

Так как определитель матрицы системы отличен от нуля, то матрица А имеет обратную и решение системы .

Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы А:

Матрица , обратная к А, имеет вид

Матричное решение системы имеет вид:

отсюда следует, что

в) Решим систему методом Гаусса. Метод Гаусса – это метод последовательного исключения неизвестных. Для удобства выпишем расширенную матрицу из коэффициентов при неизвестных и столбца свободных членов и будем приводить её к диагональному виду.

Запишем систему из коэффициентов последней матрицы

Пример 3. Найти общее решение однородной системы алгебраических уравнений:

Решение.

Получим систему

Пусть - базисные неизвестные, тогда – свободные неизвестные.

Таким образом, множество решений имеет вид:

ЗАДАНИЕ 3 по теме “Собственные значения и собственные векторы матрицы”.

Вектор-столбец 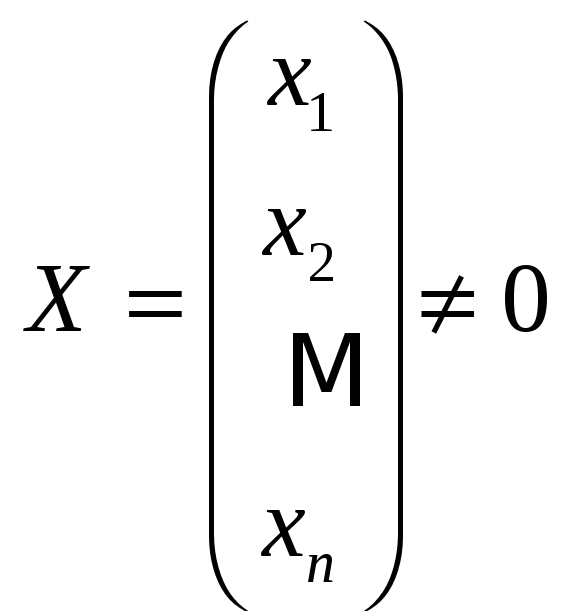называется собственным вектором квадратной матрицы А n-го порядка, соответствующим собственному значению , если он удовлетворяет матричное уравнение АХ = Х или (А – Е)Х = 0.

Здесь Е – единичная матрица n-го порядка, а 0 – нулевой вектор-столбец. При условии, что вектор Х  0 , получаем характеристическое уравнение для определения собственных значений :

det (А – Е) = 0.

Координаты собственного вектора , соответствующие собственному значению , являются решением системы уравнений

Собственный вектор определяется с точностью до постоянного множителя.

Пример 4. Найти собственные значения и собственные векторы матрицы

.

Решение. Составим характеристическое уравнение матрицы А

–(4–)(2–) + 3(2-) = 0; (2–)(–(4–)+3) =0;

(2–)(²–4+3) = 0; 2- = 0 ²-4+3 = 0;

₁ = 2; ₂ =1; ₃ = 3; ₁ = 2; ₂ =1; ₃ = 3

и являются собственными значениями матрицы А.

Для отыскания собственных векторов надо использовать систему уравнений

Полагая , получим систему для первого собственного вектора :

Следовательно, первый собственный вектор есть

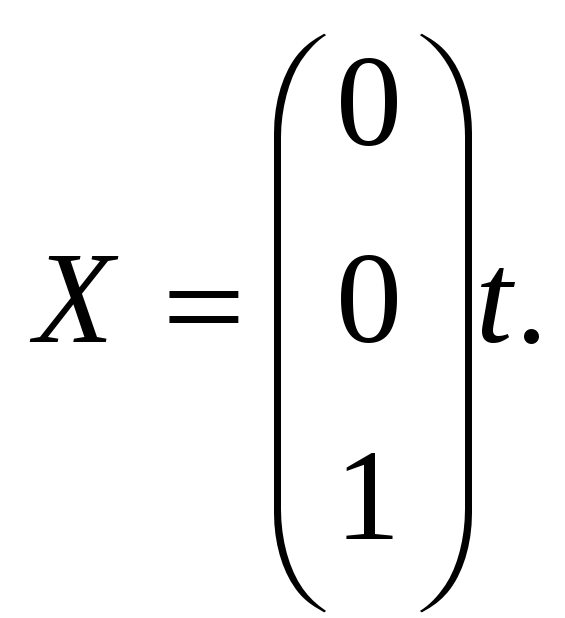
Полагая , получим систему для второго собственного вектора :

Следовательно, второй собственный вектор есть

Полагая , получим систему для первого собственного вектора :

Следовательно, третий собственный вектор есть

ЗАДАНИЕ 4 по теме “Элементы векторной алгебры”.

Вектор - это направленный отрезок, длина которого а называется модулем вектора, пишут

Два вектора и называются противоположными; для них справедливо равенство: = . Два коллинеарных ( параллельных) вектора и отличаются скалярным множителем : =  .

Разложение вектора по координатным осям 0x, 0y и 0z записывается в виде или ,

где x, y, z – проекции вектора на оси 0x, 0y и 0z; – единичные векторы (орты), совпадающие по направлению с этими осями. Проекции x, y, z называются координатами вектора.

Длина вектора определяется по формуле .

Если известны координаты точек и , то .

Если два вектора и коллинеарны, то их координаты пропорциональны, т.е.

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

Если векторы заданы своими координатами, то .

Векторным произведением двух векторов и называется третий вектор, длина которого численно равна площади параллелограмма, построенного на двух данных. Этот вектор перпендикулярен к плоскости параллелограмма и направлен так, что, если смотреть с его конца в основание, то кратчайший поворот от первого вектора ко второму виден против хода стрелки.

,

где  - угол между векторами и .

Если векторы заданы своими координатами, то

Векторное произведение равно нулю тогда и только тогда, когда векторы и коллинеарны.

Смешанным произведением трёх векторов , и называется их векторно-скалярное произведение

Если векторы заданы своими координатами смешанное произведение находится по формуле

.

Модуль смешанного произведения трёх векторов , и равен объёму параллелепипеда, построенного на векторах как на сторонах.

Система n линейно независимых векторов в n-мерном пространстве называется базисом этого пространства. По векторам базиса можно разложить любой вектор пространства, причём единственным образом.

Коэффициенты разложения вектора конечномерного линейного пространства по векторам базиса этого пространства называются координатами вектора в данном базисе.

Пример 5. Доказать, что векторы , и образуют базис, и найти координаты вектора в этом базисе

Решение. Чтобы векторы , и образовывали базис, т.е., чтобы они были линейно независимы, надо, чтобы определитель, составленный из их координат, был отличен от нуля. Составим определитель из компонент векторов , и и вычислим его:

.

Так как , то векторы , и образуют базис трёхмерного пространства. Для вычисления координат вектора в этом базисе составим системы линейных уравнений

Её решение образует совокупность координат вектора в базисе , и , т.е. в этом базисе или

Пример 6. Даны векторы . Необходимо:а) вычислить смешанное произведение трёх векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли компланарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.

а) ; б) ; в) ; г) ; д) .

Решение.

а) .

б)

в) .

г) Чтобы векторы были коллинеарны, необходимо, чтобы их соответствующие координаты были пропорциональны.

.

Векторы и не коллинеарны. Для того, чтобы два вектора были ортогональны, необходимо, чтобы их скалярное произведение равнялось нулю.

.

Значит, векторы и ортогональны.

д) Чтобы три вектора были компланарны (т.е. лежали в одной плоскости), необходимо, чтобы их смешанное произведение равнялось нулю.

Значит, векторы не компланарны.

Пример 7. Вершины пирамиды находятся в точках А, В, С, D. Вычислить: а) площадь указанной грани; б) площадь сечения, проходящего через середину ребра l и две вершины пирамиды; в) объём пирамиды АВСD.

А(2, 2, 2), В(4, 3, 3), С(4, 5, 4), D(5, 5, 6)

а) АВС; б) l = АВ, С и D.

Решение.

а) Грань пирамиды АВСD является треугольником АВС. Находим векторы и

, .

Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах и , поэтому находим векторное произведение этих векторов

=

Следовательно,

(кв. ед.)

б) Найдём координаты середины ребра l = АВ. Это точка К с координатами

Сечение является треугольником СDK. Находим векторы и

=

=

(кв. ед.)

в) Найдём векторы , , , совпадающие с рёбрами пирамиды, сходящимися в вершине А:

, , .

Находим смешанное произведение этих векторов:

Так как объём пирамиды равен объёма параллелепипеда, построенного на векторах , , , то (куб. ед.)

ЗАДАНИЕ 5 по теме “Прямая на плоскости”.

Уравнение вида Ax + By + C = 0 (А, В, С – постоянные коэффициенты) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

Уравнение прямой, разрешенное относительно y, называется уравнением с угловым коэффициентом: y = k x + b. Здесь k = tg , где  – угол, образованный прямой с положительным направлением оси 0x. Свободный член уравнения b равен ординате точки пересечения прямой с осью 0у.

Уравнение прямой, проходящей через данную точку и имеющей угловой коэффициент k, находится по формуле .

Условие параллельности прямых: .

Условие перпендикулярности прямых:

Уравнение прямой, проходящей через две заданные точки и записывается в виде:

Если даны две прямые и , то их точка пересечения находится совместным решением двух данных уравнений. Если уравнения несовместны, то прямые параллельны.

Расстояние d точки до прямой вычисляется по формуле

Пример 8. Даны вершины треугольника АВС: А(0, 1), В(6, 5), С(12, –1). Найти:

а) уравнение стороны АВ;

б) уравнение высоты СН;

в) уравнение медианы АМ;

г) точку N пересечения медианы АМ и высоты СН;

д) уравнение прямой, проходящей через вершину С параллельно стороне АВ;

е) расстояние от точки С до прямой.

Решение.

а) Найдём уравнение стороны АВ как прямой, проходящей через две заданные точки А(0,1) и В(6, 5).

4х = 6у – 6; 4х – 6у + 6 = 0; 2х – 3у + 3 = 0 – уравнение АВ.

б) Найдём угловой коэффициент стороны АВ. Для этого приведём уравнение АВ к виду с угловым коэффициентом 3у = 2х + 3

В силу условия перпендикулярности угловой коэффициент высоты, проведённой из вершины С, равен . Уравнение этой высоты имеет вид:

в) Точка М делит сторону ВС пополам, поэтому координаты точки М равны полусуммам координат В и С:

Следовательно, М(9, 2).

Составим уравнение медианы АМ как прямой, проходящей через точки А(0, 1) и М(9, 2)

х – 9у + 9 = 0 - уравнение АМ.

г) Точку N пересечения медианы АМ и высоты СН найдём, решая систему из уравнений АМ и СН:

д) Составим уравнение прямой, проходящей через вершину С параллельно стороне АВ.

2х – 3у + 3 = 0 – уравнение АВ

. В силу условия параллельности угловой коэффициент прямой, проходящей через С параллельно стороне АВ тоже равен .

е) Вычислим расстояние от точки С до прямой АВ

ЗАДАНИЕ 6 по теме “Кривые второго порядка”.

Уравнение окружности с центром в точке С(a, b) и радиусом R имеет вид:

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная ( её обозначают 2а). Расстояние между фокусами обозначают через 2с.

Простейшее уравнение эллипса

Здесь а – большая, b – малая полуось эллипса.

Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а).

Простейшее уравнение гиперболы

Здесь 2а – действительная ось гиперболы, 2b – мнимая ось гиперболы.

Прямая называется асимптотой гиперболы, если расстояние точки М(х, у) гиперболы от этой прямой стремиться к нулю при или . Гипербола имеет асимптоты, уравнения которых

Эксцентриситет гиперболы

Параболой называется множество точек плоскости, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Если директрисой параболы является прямая , а фокусом – точка, то уравнение параболы имеет вид

Пример 9. Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы (А, В – точки, лежащие на кривой, F – фокус, а – большая (действительная) полуось, b – малая (мнимая) полуось, е – эксцентриситет, - уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние.

а) b = 4, F(5, 0);

б) а = 5, е = 1,4;

в) ось симметрии 0у и А(1,-2).

Решение.

а) У нас b = 4, с = 5. Чтобы написать уравнение эллипса, следует найти большую полуось а. Между величинами a, b, c у эллипса существует зависимость:

Уравнение эллипса будет иметь вид:

б) а = 5; е = 1,4; .

Найдём с: с = еа = 1,4  5 = 7.

Для гиперболы ;

Уравнение гиперболы

в) Данная парабола симметрична относительно оси 0у и проходит через точку с отрицательной ординатой, поэтому она имеет уравнение вида Подставим в это уравнение координаты точки А:

1 = –2р(–2);

Следовательно, искомое уравнение , или

ЗАДАНИЕ 7 по теме “Прямая и плоскость в пространстве”.

Ах + Ву + Сz + D = 0 – общее уравнение плоскости.

Угол между двумя плоскостями и определяется по формуле

Условие перпендикулярности двух плоскостей имеет вид:

Условие параллельности двух плоскостей имеет вид:

Расстояние от точки N() до плоскости Ах + Ву + Сz + D = 0 определяется по формуле:

.

Уравнение плоскости, проходящей через три данные точки , , имеет вид:

.

Каноническое уравнение прямой в пространстве:

где - координаты точки, через которую проходит прямая, а m, n, p – направляющие коэффициенты прямой.

Уравнение прямой, проходящей через две данные точки и запишется в виде:

Угол между двумя прямыми и определяется по формуле:

.

Условие перпендикулярности двух прямых в пространстве имеет вид:

Условие параллельности двух прямых в пространстве имеет вид:

Острый угол между прямой и плоскостью определяется по формуле

Условие параллельности прямой и плоскости в пространстве имеет вид:

Условие перпендикулярности прямой и плоскости в пространстве имеет вид:

Пример 10. Даны четыре точки , , , . Составить уравнение: а) плоскости ; б) прямой ; в) прямой , перпендикулярной к плоскости ; г) прямой , параллельной прямой ; д) плоскости, проходящей через точку перпендикулярно к прямой . Вычислить: е) синус угла между прямой и плоскостью ; ж) косинус угла между координатной плоскостью 0ху и плоскостью .

Решение.

а) Составим уравнение плоскости как плоскости, проходящей через три точки .

Раскрывая определитель, получим :

б) Составим уравнение прямой как прямой, проходящей через две точки и :

в) Напишем прежде всего уравнение прямой, проходящей через данную точку :

Из условия перпендикулярности данной прямой и плоскости имеем: поэтому уравнение прямой , перпендикулярной к плоскости имеет вид

.

г) Напишем уравнение прямой, проходящей через точку :

.

Из условия параллельности двух прямых заключаем, что m, n, p должны быть пропорциональны направляющим коэффициентам прямой , т.е.

Поэтому уравнение прямой , параллельной прямой имеет вид:

д) Уравнение всех плоскостей, проходящих через точку имеет вид:

Уравнение всех плоскостей, проходящих через точку будут имеет вид:

Пользуясь условием перпендикулярности прямой и плоскости, заменив в последнем уравнении величины А, В, С им пропорциональными величинами m, n, p из уравнения прямой , т.е. числами 3, –3, –5, получим

е) Синус угла между прямой и плоскостью вычислим, пользуясь формулой для вычисления между прямой и плоскостью.

Составим уравнение прямой :

Уравнение плоскости : ; m = 1, n = –1, p = 3, A = –10, B = –15, C = 3

ж) Уравнение координатной плоскости 0ху имеет вид: z = 0.

Вычислим косинус угла между координатной плоскостью 0ху и плоскостью , пользуясь формулой определения угла между двумя плоскостями:

ЗАДАНИЕ 8 по теме “Предел функции”.

Пример 11. Найти указанные пределы:

а)

Подстановка числа х = 1 под знак предела приводит к неопределённости вида . Разложим числитель и знаменатель на множители и сократим на х – 1:

б)

Здесь неопределённость вида . В подобных случаях следует числитель и знаменатель разделить на самую высокую входящую в них степень x:

Вообще: при предел отношения двух многочленов одинаковых степеней равен отношению коэффициентов при старших степенях х; если же степени многочленов не равны, то предел их отношения равен нулю, если степень числителя меньше степени знаменателя, и равен бесконечности, если степень числителя больше степени знаменателя.

в)

Здесь неопределённость вида . В примерах, имеющих такую неопределённость, следует воспользоваться вторым замечательным пределом:

Преобразовав выражение, получим:

г)

Здесь имеем неопределённость вида . Чтобы её раскрыть, умножаем числитель и знаменатель на выражение, сопряжённое числителю. После этого можно будет сократить на

д)

Здесь имеем неопределённость вида . При вычислении предела будем пользоваться первым замечательным пределом:

ЗАДАНИЕ 9 по теме “Непрерывность и точки разрыва”.

Функция называется непрерывной в точке а, если:

1. эта функция определена в некоторой окрестности точки а;

2) существует ;

3) этот предел равен значению функции в точке а, т.е. .

Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.

Если существуют конечные пределы , причем не все три числа равны между собой, то а называется точкой разрыва І рода.

Если хотя бы один из односторонних пределов не существует (в частности равен бесконечности), то разрыв в точке а является разрывом II рода.

Пример 12. Найти точки разрыва функций, если они существуют. Сделать чертёж.

а)

Решение. Так как данная функция определена на всей числовой оси, то “подозрительными на разрыв” являются те точки, в которых изменяется аналитическое выражение функции, т.е. точки х = –1 и х = 1. Вычислим односторонние пределы в этих точках.

Для точки х = –1 имеем:

Односторонние пределы равны между собой, поэтому исследуемая точка является точкой непрерывности.

Для точки х = 1 имеем:

Односторонние пределы функции в точке х = 1 существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва I рода.

б) .

Эта функция является дробно-рациональной, и поэтому она непрерывна во всех точках, в которых знаменатель отличен от нуля. В точке х = 3 эта функция не определена, и поэтому разрывна. Вычислим односторонние пределы в этой точке.

Односторонние пределы бесконечные и поэтому, х = 3 – точка разрыва функции II рода.

Для более точного построения графика функции исследуем поведение функции на бесконечности.

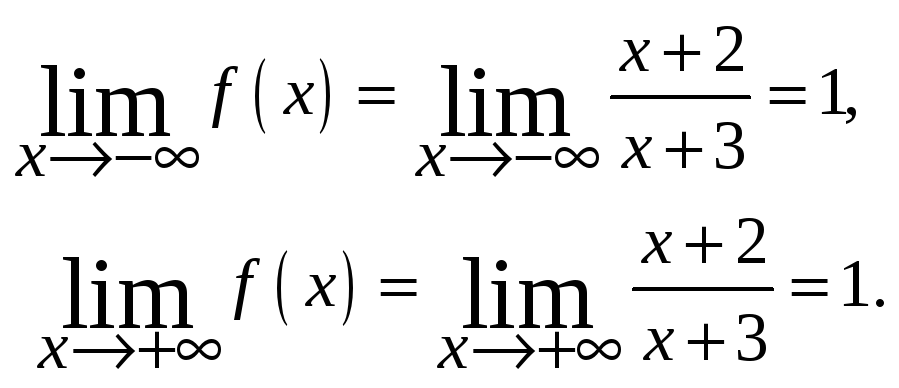
З начит, у = 1 – горизонтальная асимптота данной функции.

в) .

Данная функция непрерывна везде, за исключением точки х = –1. Для выяснения характера разрыва в этой точке найдём пределы слева и справа:

Следовательно, х = -1 – точка разрыва функции II рода, так как предел справа бесконечный.

Для более точного построения графика функции исследуем поведение функции на бесконечности.

З начит, у = 1 – горизонтальная асимптота данной функции.

ЗАДАНИЕ 9 по теме “Производная функции”.

Производной от функции в точке х называется предел отношения её приращения в этой точке к соответствующему приращению аргумента , когда последнее стремится к нулю.

.

Операция нахождения производной называется дифференцированием.

Основные правила дифференцирования

Основные формулы дифференцирования

Пример 13. Продифференцировать данные функции:

а)

б)

в)

г)

д) .

В данном примере прежде чем дифференцировать функцию, удобно её прологарифмировать, а затем найти производную как от неявной функции

.

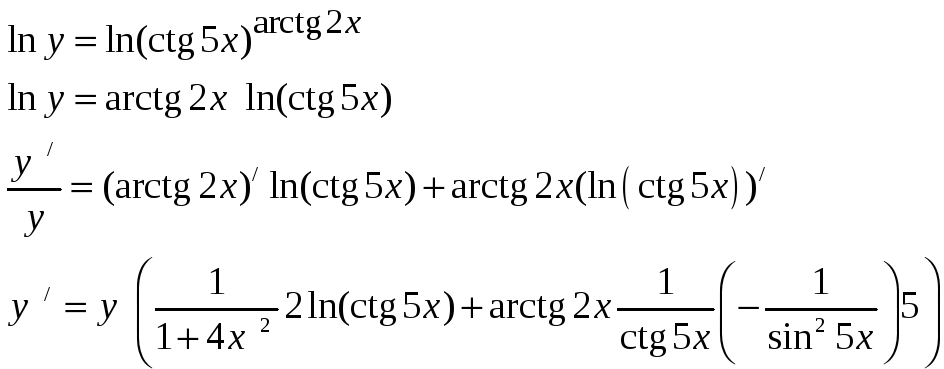
е)

В данном примере удобно функцию сначала прологарифмировать

Пример 14. Найти и .

а) arctg y – y + x = 0

Дифференцируем заданное соотношение, рассматривая у как функцию от х:

Находим далее :

В правую часть последнего равенства подставляем вместо его значение

.

б)

Если функция задана параметрическими уравнениями , то её производная находится по формуле : .

Вторая производная находится по формуле :

;

;

ЗАДАНИЕ 10 по теме “Вычисление пределов по правилу Лопиталя”.

Правило Лопиталя. Если функции и бесконечно малые или бесконечно большие при , дифференцируемы в окрестности точки , в окрестности этой точки, существует , то существует и справедливо равенство: .

Эта теорема справедлива и при и позволяет раскрывать неопределённости и . Другие виды неопределённостей приводят к этим двум преобразованием выражения под знаком предела.

Пример 15. Найти указанные пределы, используя правило Лопиталя.

а)

Здесь неопределённость вида . Применяя правило Лопиталя, имеем

б)

Здесь для получения результата приходится применять правило Лопиталя дважды, так как и данное отношение и отношение производных приводят к неопределённости типа . Повторные применения правила Лопиталя записываются обычно в одну цепочку равенств.

в)

Здесь неопределённость вида . Положим . Логарифмируя и применяя правило Лопиталя, получим

Таким образом,

г)

Это – неопределённость вида . Положим и прологарифмируем:

Применяя правило Лопиталя, получим

, т.е.

ЗАДАНИЕ 11 по теме “Исследование функции с помощью производной”.

Если в некоторой окрестности точки выполняется неравенство или , то точка называется точкой экстремума функции (соответственно точкой максимума или минимума). Необходимое условие экстремума: если – экстремальная точка функции , то первая производная либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: является экстремальной точкой функции , если её первая производная меняет знак при переходе через точку : с плюса на минус – при максимуме, с минуса на плюс – при минимуме.

Кривая вогнута вверх (обозначают  ) на интервале , если в каждой точке этого интервала выполнено условие при и вогнута вниз (обозначают  ), если при .

Точка называется точкой перегиба кривой , если при переходе через точку меняется направление выпуклости. Необходимое условие точки перегиба: если - точка перегиба кривой , то вторая производная либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба: является точкой перегиба кривой , если при переходе через точку вторая производная меняет знак.

Прямая является наклонной асимптотой кривой , если расстояние от точки кривой до этой прямой стремится к нулю при . При этом

.

При имеем горизонтальную асимптоту:

Если то прямая называется вертикальной асимптотой.

Общая схема построения графика функции

1. Найти область определения.

2. Четность, нечетность.

3. Определить точки пересечения графика функции с координатными осями.

4. Найти интервалы монотонности и точки экстремума функции.

5. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба.

6. Выяснить существование асимптот.

7. Построить график функции.

Пример 16. Найти наибольшее и наименьшее значения функции на отрезке .

Решение. Наибольшее и наименьшее значения функции на замкнутом интервале достигаются или в точках экстремума, которые являются критическими точками функции, или на концах интервала. Задача сводится к сравнению между собой значений функции в указанных точках.

Находим стационарные точки:

Определяем значение функции в этих точках и на концах интервала

Среди полученных значений выбираем наибольшее и наименьшее

Пример 17. Провести полное исследование указанных функций и построить их графики.

а) .