
Struktura_danikh_Ch1
.pdfPrtKLP(LeftSon(t));
PrtKLP(RightSon(t)) end
end;
procedure PrtLKP(t: btree); begin
if Empty(t) then write(' ,') else begin PrtLKP(LeftSon(t)); write(Root(t),','); PrtLKP(RightSon(t)) end
end;
procedure PrtLPK(t: btree); begin
if Empty(t) then write(' ,') else begin PrtLPK(LeftSon(t)); PrtLPK(RightSon(t)); write(Root(t),',');
end end;
var t: btree; begin
t:=MakeTree(1,MakeTree(2,MakeTree(3,Init,Init),MakeTree(4,Init,Init)),
MakeTree(5,MakeTree(6,Init,Init),Init));
writeln;
writeln('Число вузлів ',NodeCount(t)); write('КЛП='); PrtKLP(t); writeln; write('ЛКП='); PrtLKP(t); writeln; write('ЛПК='); PrtLPK(t); writeln; end.
В результаті роботи програми BtreeTst на екрані буде показано:
Число вузлів 6
КЛП=1,2,3, , ,4, , ,5,6, , , ,
ЛКП= ,3, ,2, ,4, ,1, ,6, ,5, , ЛПК= , ,3, , ,4,2, , ,6, ,5,1,
63
4.2 Сильно розгалужене дерево
Сильно розгалуженим називають дерево, в якому напівступінь виходу вершин більше 2. Реалізація сильно розгалужених дерев залежить від того, чи відома максимальна напівступінь виходу вершин. Якщо вважати, що максимальна напівступінь виходу не визначена. Тоді кожну вершину сильно розгалуженого дерева можна представити навантаженням та списком синів. Відповідно, всі дії над деревом можна розбити на дві групи: дії над вершинами дерева та дії над списком синів. Якщо використати у якості списку список з поточним елементом. Тоді операції, відношення та інструкції для сильно розгалужених дерев можна визначити так:
1Почати роботу.
2Чи порожнє дерево?
3Створити вершину.
4Корінь дерева.
5Список синів.
6Видалити вершину.
7Почати роботу із списком синів.
8Чи порожній залишок списку синів?
9Встати до початку списку синів.
10Перейти до наступного елемента списку синів.
11Поточний елемент списку синів.
12Вставити елемент у список синів.
13Видалити елемент списку синів.
Дії 1, 3, 6 – інструкції, 4, 5 – операції; 2 – відношення. Інструкція “Почати роботу” створити порожнє дерево.
“Створити вершину” – за списком дерев l та даними n створити дерево з коренем з навантаженням n та списком синів l.
“Корінь дерева” повертає навантаження кореня дерева. Дерево при цьому не змінюється. Для порожнього дерева ця операція повинна давати відмову.
“Список синів” повертає список дерев, які є синами даної вершини. Для порожнього дерева ця операція не визначена.
“Видалити вершину” видалити поточну вершину дерева. Для порожнього дерева ця інструкція повинна давати відмову.
Можлива реалізація сильно розгалуженого дерева з використанням вказівників зображена на рис. 4.6. Вершини дерева – це записи з двох полів: поле даних та список синів (який, в свою чергу, є записом з двох вказівників: на початок списку та на поточний елемент списку). За допомогою вказівників вершини дерева з’єднані між собою. На рисунку вказівники на вершини позначені жирними стрілками, а вказівники у списку синів – тонкими. Саме дерево – це вказівник на корінь. Якщо дерево порожнє, то вершин немає, а вказівник дорівнює nil.
64
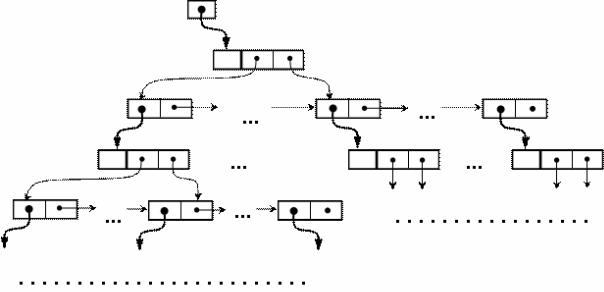
Рисунок 4.6 - Реалізація сильно розгалуженого дерева
Інтерфейсна частина модуля мовою Паскаль для сильно розгалужених дерев має вигляд:
unit IntTree; |
|
|
interface |
|
|
type tree = ^node; |
{Дерево} |
|
lref = ^lelem; |
{Вказівник на елемент списку} |
|
lelem = record |
{Елемент списку} |
|
nd: tree; |
|
|
next: lref |
|
|
end; |
|
|
list = record |
{Список дерев} |
|
beg, cur: lref |
|
|
end; |
|
|
node = record |
{Вершина дерева} |
|
d: integer; |
|
|
sl: list |
|
|
end; |
|
|
procedure Init(var t: tree); |
{ Почати роботу } |
|
function Empty(t: tree): boolean; |
{ Чи порожнє дерево? } |
|
procedure MakeNode(var t: tree; n: integer; l: list);{ Створити вершину }
function Root(t: tree): integer; |
{ Корінь дерева } |
procedure SonsList(t: tree; var l: list); |
{ Список синів } |
procedure DelNode(var t: tree); |
{ Видалити вершину } |
procedure SlInit(var l: list); |
{ Почати роботу із списком } |
|
65 |
function SlEmpEnd(l: list): boolean; procedure SlFirst(var l: list); procedure SlNext(var l: list); function SlCurrent(l: list): tree; procedure SlInsert(var l: list; t: tree); procedure SlDelete(var l: list); implementation
.................
end.
{Чи порожній залишок списку?}
{Встати до початку списку }
{Перейти до наступного елемента}
{Поточний елемент списку}
{Вставити елемент у список}
{Видалити елемент списку}
4.3 Граф
Для роботи з графами існують різні реалізації. Відома, наприклад, реалізація графа у вигляді матриці суміжності (матриці з 0 та 1, де 1 стоїть у комірці матриці, яка відповідає вершинам графа vi, vj, пов’язаних дугою). Така реалізація досить проста, але не економить пам’ять, особливо для розріджених графів. Більш загальною є реалізація графів, в яких для кожної вершини складається список вершин, з яких у дану вершину входять дуги (попередники) та список вершин, у які з даної вершини виходять дуги (наступники). Сам граф також можна подати у вигляді списку вершин.
Перелік операцій, відношень та інструкцій для графів:
1Створити вершину.
2Навантаження вершини.
3Список попередників.
4Список наступників.
5Змінити список попередників.
6Змінити список наступників.
7Видалити вершину.
8Почати роботу із списком вершин.
9Чи порожній залишок списку вершин?
10Встати до початку списку вершин.
11Перейти до наступного елемента списку вершин.
12Поточний елемент списку вершин.
13Вставити елемент у список вершин.
14Видалити елемент списку вершин.
Дії 1 – 7 – це дії над вершинами графа, а дії 8 – 14 – це дії із списком з поточним елементом. Далі розглядатимуться лише дії безпосередньо над вершинами графа 1 - 7.
Дії 1, 5, 6, 7 – інструкції, 2, 3, 4 – операції.
“Створити вершину” – за списками вершин l1, l2 та даними n створити вершину графа з навантаженням n, списком попередників l1 та списком наступників l2.
66
“Навантаження вершини” повертає навантаження даної вершини. Вершина при цьому не змінюється.
“Список попередників” повертає список вершин, які є попередниками даної вершини.
“Список наступників” повертає список вершин, які є наступниками даної вершини.
“Змінити список попередників” замінює список попередників даної вершини даним списком вершин.
“Змінити список наступників” замінює список наступників даної вершини даним списком вершин.
“Видалити вершину” видалити дану вершину графа.
Наведений набір дій над графами є скоріше набором так званих “мікрооперацій”, на базі яких можна реалізовувати “великі” операції над графами. Наприклад, додавання вершини графа повинно включати створення списку попередників, списку наступників, створення вершини та безпосередньо вставку вершини у граф. До того ж, під час додавання вершини треба модифікувати списки наступників всіх вершин, які є попередниками нової, та списки попередників всіх вершин, які є наступниками нової, включивши у ці списки дану вершину.
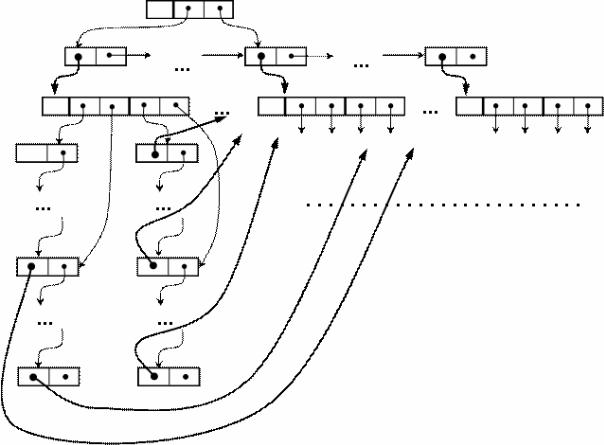
Можлива реалізація графа з використанням вказівників зображена на рис. 4.7. Вершини графа – це записи з трьох полів: поле даних, список наступників та список попередників (які, в свою чергу, є записами з двох вказівників: на початок списку та на поточний елемент списку). За допомогою вказівників вершини графа з’єднані між собою. На рисунку вказівники на вершини позначені жирними стрілками, а вказівники у списках вершин – тонкими. Сам граф, список попередників вершини, список наступників вершини – це списки вершин.
Реалізація графів мовою Паскаль представлена у модулі IntGraph. В цьому модулі новими є тільки реалізації дій створення вершини, отримання та зміни списку попередників. Інші дії над вершинами дуже прості або схожі на розглянуті, а дії над списками з поточним елементом були розглянуті раніше.
67
|
Рисунок 4.7 - Реалізація графа |
unit IntGraph; |
|
interface |
|
type |
|
noderef = ^node; |
{Вказівник на вершину графа} |
lref = ^lelem; |
{Вказівник на елемент списку вершин} |
lelem = record |
{Елемент списку вершин} |
nd: noderef; |
|
next: lref |
|
end; |
|
graph = record |
{Список вершин (граф)} |
beg, cur: lref |
|
end; |
|
node = record |
{Вершина графа} |
d: integer; |
|
pl, sl: graph |
|
end; |
|
procedure MakeNode(var nod: noderef; n: integer; l1, l2: graph);{Створити
вершину} |
|
function Weight(nod: noderef): integer; |
{ Навантаження вершини } |
|
68 |
procedure GetPredList(nod: noderef; var l: graph); |
{ Список попередників } |
||
procedure GetSuccList(nod: noderef; var l: graph); |
{ Список наступників } |
||
procedure SetPredList(nod: noderef; l: graph);{Змінити список попередників} |
|||
procedure SetSuccList(nod: noderef; l: graph);{Змінити список наступників } |
|||
procedure DelNode(var nod: noderef); |
{ Видалити вершину } |
||
procedure Init(var g: graph); |
{ Почати роботу із списком вершин } |
||
function EmpEnd(g: graph): boolean; |
{ |
Чи порожній залишок списку |
|
вершин?} |
|
|
|
procedure First(var g: graph); |
{ Встати до початку списку вершин } |
||
procedure Next(var g: graph); |
{ Перейти до наступного елемента } |
||
function Current(g: graph): noderef; |
{ Поточний елемент списку вершин } |
||
procedure Insert(var g: graph; nod: noderef); |
{ Вставити елемент } |
||
procedure Delete(var g: graph); |
{ Видалити елемент списку вершин } |
||
implementation
.................
procedure MakeNode(var nod: noderef; n: integer; l1, l2: graph); begin
new(nod);
nod^.d:=n; nod^.pl:=l1; nod^.sl:=l2 end;
.................
procedure GetPredList(nod: noderef; var l: graph); begin
l:=nod^.pl
end;
.................
procedure SetPredList(nod: noderef; l: graph); begin
nod^.pl:=l
end;
.................
end.
Як приклад використання графів можна навести програму, яка перевіряє, чи є граф деревом. Функція Len обчислює довжину списку вершин. Функція FindRoot обчислює номер вершини, яка є коренем дерева, тобто має напівступінь входу 0. Якщо така вершина є і вона у графі єдина, FindRoot повертає її номер у списку, інакше FindRoot повертає 0. Процедура TestTree(nod, b, k) перевіряє, чи є частина графа, яка починається з nod деревом (тоді значення b - істина) та повертає у змінній k кількість вершин цього дерева. Процедура InsLink(nod, g, n) пов’язує дугою вершину nod графа g з вершиною цього графа з номером n, модифікуючи список попередників вершини nod та список наступників вершини з номером n. Ця процедура викликається у
69
процедурі введення графа InputGraph. Остання процедура спочатку вводить навантаження всіх вершин графа, формує граф з порожніми списками попередників та наступників. Потім вводяться всі дуги графа. Основна програма організує введення графа, перевіряє, чи є він деревом та показує результат.
Program GraphTst; uses IntGraph;
function Len(g: graph): word; var l: word;
begin
l:=0; First(g);
while not EmpEnd(g) do begin l:=l+1;
Next(g)
end;
Len:=l
end;
function FindRoot(g: graph): word; var k, n, i: word;
b, c: boolean; nod: noderef; l: graph;
begin
k:=0; c:=true; b:=false; First(g); i:=0;
while not EmpEnd(g) and c do begin nod:=Current(g); i:=i+1; GetPredList(nod, l);
if Len(l)=0 then begin n:=i;
b:=true; k:=k+1; c:=k<=1
end;
Next(g)
end;
if b and c then FindRoot:=n else FindRoot:=0
end;
procedure TestTree(nod: noderef; var b: boolean; var k: word); var nod1: noderef;
sl, pl: graph; begin
70
k:=k+1;
GetSuccList(nod,sl); First(sl); b:=true;
while not EmpEnd(sl) and b do begin nod1:=Current(sl); GetPredList(nod1,pl); TestTree(nod1, b, k);
b:=b and (Len(pl)=1); Next(sl)
end;
end;
procedure InsLink(nod: noderef; g: graph; n: word); var nod1: noderef;
pl,sl: graph; i: word;
begin First(g);
for i:=1 to n-1 do Next(g); nod1:=Current(g);
GetSuccList(nod,sl); GetPredList(nod1,pl); Insert(sl,nod1); Insert(pl,nod); SetSuccList(nod,sl); SetPredList(nod1,pl); end;
procedure InputGraph(var g: graph); var n, i, m, j, n1: word;
k: integer; l1, l2: graph; nod: noderef;
begin Init(g);
write('Кількість вершин: '); readln(n); Init(l1); Init(l2);
for i:=1 to n do begin write('Навантаження вершини ',i,': '); readln(k);
MakeNode(nod,k,l1,l2);
Insert(g,nod)
end;
First(g);
for i:=1 to n do begin nod:=Current(g);
write('Кількість наступників для вершини ',i,': ');
71
readln(m);
for j:=1 to m do begin repeat
write('Номер ',j,' наступника[1-',n,']: '); readln(n1);
until (n1>=1) and (n1<=n); InsLink(nod,g,n1);
end; |
|
Next(g) |
|
end; |
|
end; |
|
var g: graph; |
|
n,k,m,i: word; |
|
b: boolean; |
|
nod: noderef; |
|
begin |
|
InputGraph(g); |
{введення графа} |
n:=Len(g); |
{обчислення кількості вершин} |
m:=FindRoot(g); |
{пошук номера вершини - кореня дерева} |
b:=m<>0; |
{якщо m<>0, то вершина з номером m - корінь} |
if b then begin |
|
First(g);
for i:=1 to m-1 do Next(g);
nod:=Current(g); |
{nod - вказівник на вершину - корінь дерева} |
k:=0; |
|
TestTree(nod,b,k); |
{перевірка, чи є частина графа, починаючи з nod, |
деревом} |
|
b:=b and (k=n); {граф є деревом, якщо кількість вершин k дорівнює n} end;
if b then
writeln('Граф - дерево з коренем ',m,' з навантаженням ',Weight(nod)) else writeln('Граф не є деревом')
end.
Питання для самоконтролю
1Дайте визначення дерева.
2Дайте визначення бінарного дерева.
3Які операції можна виконувати над бінарним деревом?
4Опишіть функцію створення бінарного дерева.
5Які типи обходів бінарних дерев Ви знаєте, опишіть їх?
6Дайте визначення сильно розгалуженого дерева.
7Які операції можна виконувати над сильно розгалуженим деревом?
8Які операції можна виконувати над графом?
72
