4.2. Виконання індивідуальних завдань.

4.2.1. Спрощення виразу.

1. За допомогою панелі Символика (Simplify)

2. За допомогою команди Символика/Упростить

упрощает к

4.2.2. Робота з поліномами високих порядків.

4.2.2.1. Розкладання полінома на множники.

1.За допомогою панелі Символика/Factor:

2.За допомогою меню Символика/Фактор:

4.2.2.2. Заміна змінної виразом.

Підставити вираз x=y+z в g(x):

1.За допомогою меню Символика/Переменные/Замена

3. За допомогою панелі

4.2.2.3. Визначення коренів полінома.

Визначити корені полінома g(x) за допомогою функції polyroots().

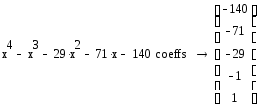
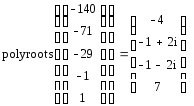
4.2.3. Розкладання виразу на елементарні дроби.

1.За допомогою меню Символика/Переменные/Преобразование в частичные доли (в простую дробь)

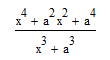
2.За допомогою панелі

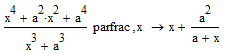
4.2.4. Розкладання виразу в ряд з заданою точністю.

Розкласти вираз в ряд з заданою точністю, x(0)=0, порядок розкладу n=6, використавши команду Символика/Переменные/ Разложить на составляющие (Расширить до рядов).

1. За допомогою меню

2. За допомогою панелі

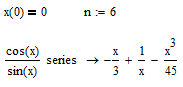
4.2.5. Знаходження первісної аналітично заданої функції.

Знайти первісну аналітично заданої функції f(x), використавши команду Символика/Переменные/Интеграция.

1. За допомогою меню

2. За допомогою панелі

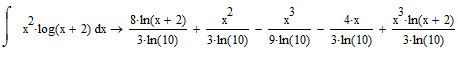
4.2.6. Знаходження символьного значення першої і другої похідних аналітично заданої функції.

Визначити символьне значення першої і другої похідних f(x), використавши команду Символика/Переменные/Дифференциалы

1. За допомогою меню

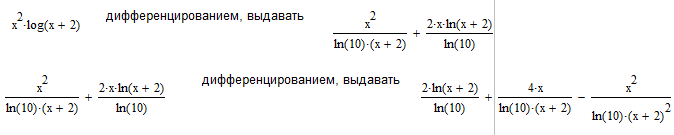
2. За допомогою панелі

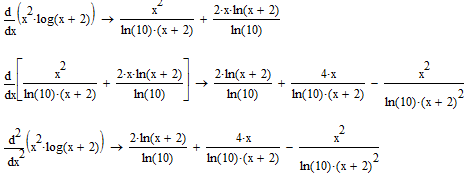
4.2.7. Робота з матрицями.

Транспортуйте матрицю за допомогою команди Символика /Матрицы/ Транспонирование.

1.За допомогою меню

2.За допомогою панелі

Інвертуйте матрицю за допомогою команди Символика/Матрицы/ Инвертирование.

1.За допомогою меню

2.За допомогою панелі

Обчисліть визначник матриці за допомогою команди Символика/ Матрицы/ Определитель.

1.За допомогою меню

2.За допомогою панелі

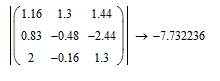
4.2.8. Обчислення границь.

Обчисліть межу.

1.За допомогою меню

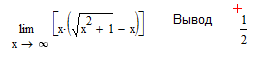
2.За допомогою панелі

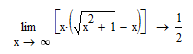
4.2.9.Знайти рішення рівняння в символьному вигляді.

1.За допомогою меню

2.За допомогою панелі

5. Рішення диференційних рівнянь з використанням пакету MathCad.

5.1. Постановка задачі

5.2. Теоретичні відомості з інтегрування диференційних рівнянь.

Розв’язування диференціального рівняння. Постановка задачі (задача Коші) має вигляд диференціального рівняння з початковими умовами:

yР = f(t,y), y = y0 при t = t0. t Є [a, b].

Для її наближеного розв’язання застосовуються так звані однокрокові методи: Ейлера, Ейлера покращений, Ейлера-Коші та Рунге-Кута. Їх суть полягає в тому, що діапазон інтегрування [a, b] ділять на n елементарних відрізків довжиною h. Значення шуканої функції в точці t0=a відомо з початкових умов, а її обчислення в першій і наступних точках аж до точки tn=b виконують за поданими нижче формулами. При цьому h=(b-a)/n, t0 = a, tn = b, ti+1 = ti+h, yi=f(ti), i=0,1,2, ... n.

5.3. Виконання індивідуального завдання.

5.3.1. Розв’язання методами Ейлера та Рунге-Кутта.

5.3.2. Розв’язання засобами MathCad.

5.3.3. Розв’язання системи диференційних рівнянь засобами MathCad.

6. Інтерполяція та апроксимація табличних функцій методом найменших квадратів з використанням пакету MathCad.

6.1. Постановка задачі.

6.2. Теоретичні відомості з інтерполяції та апроксимації функцій, заданих таблично.

У процесі пошуку закономірностей протікання явищ та процесів в інженерній практиці виникає задача відшукання за даними спостережень аналітичних залежностей одного параметра від іншого. Загальна постановка цієї задачі може бути наступна: - відомо, що між х та y існує функціональна залежність. В результаті експерименту отримана таблиця значень y₀(x₀), y₁(x₁), y₂(x₂) ,…, y_n(x_n). Необхідно знайти функцію, яка б наближено описувала зв’язок між х та y. В багатьох випадках в якості емпіричної залежності вибирається многочлен вигляду y=a₀+a₁x+…+a_mx_m. Однак, незалежно від виду апроксимуючої функції, виникає задача визначення таких її параметрів, які б найкращим чином узгоджувались з експериментальними даними. Одним з таких ефективних методів являється метод найменших квадратів. Суть методу в тому, що є залежність f(x,a₀,a₁…a_m), близька до заданої сукупності значень х_i,y_i в сенсі мінімуму квадратичного відхилення:

R=(f(x_i,a₀,a₁,…a_m)-y_i)², i=1,2,..n (1.1)

а відхилення апрoксимуючої функції від експериментальних значень

_i= f(x_i,a₀,a₁,…a_m)-y_i,,i=1,2,..n (1.2)

Тоді задача полягає у виборі сукупності параметрів a₀,a₁,…a_m, при яких значення критерія (4.1) являється мінімальним. Необхідною умовою мінімуму критерія (4.1) являється рівенство нулю всіх частинних похідних функції R по параметрах a₀,a₁,…a_m, тобто,

(∂R/∂a₀)=0, (∂R/∂a₁)=0,…, (∂R/∂a_m)=0 (1.3)

Розв’язуючи систему рівнянь (1.3) знаходимо значення a₀,a₁,…a_m які будуть коефіцієнтами шуканої залежності.

Лінійне наближення має вигляд y=a₀+a₁x. коефіцієнти якого знаходять зі слідуючої системи рівнянь:

(n+1)a₀+ a₁ x_i= y_i

a₀ x_i + a₁ x²_i= x_i y_i

Квадратичне наближення має вигляд y=a₀+a₁x+a₂x². Коефіцієнти a₀,a₁,a₂ обчислюються з системи рівнянь:

a₀ (n+1) + a₁ x_i+ a₂ x²_i = y_i

a₀ x_i + a₁ x²_i+ a₂ x³_i = x_i y_i

a₀ x²_i+ a₁ x³_i+ a₂ x⁴_i = x²_i y_i

Задача апроксимації – перехід від таблично заданої функції

y₀(x₀),y₁(x₁),y₂(x₂) ,…, y_n(x_n)

до стандартного математичного представлення:

y=a₀φ₀(x)+ a₁φ₁(x)+…+ a_nφ_n(x),

де φ_і(x) - попередньо задані (базисні) функції;

а_і - коефіцієнти розвинення функції у(х) по обраному базису.

В залежності від вигляду φ_і(x) розрізняють:

• поліноміальну апроксимацію (φ_і(x)=х^і);

• гармонічну апроксимацію (φ_і(x)=sin(iωx+α_i)).

Частіше всього вимагається мінімізація середньоквадратичної похибки апроксимації (апроксимація за методом найменших квадратів) або співпадіння вихідної та апроксимуючої функцій в точках x₀,x₁,…,x_n (інтерполяція). Широко відоме розвинення функції в ряд Фур’є

Y(x)=A₀ + B_1s sinωx + B_1c cosωx +…+ B_ks sinkωx + B_kc coskωx +…

яка являє собою гармонічну апроксимацію за методом найменших квадратів, а представлення функції поліномом Лагранжа

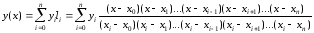
являється поліноміальною інтерполяцією.