
11 ALGEBRA
.pdf
Remark
If the interest is compounded continuously, the compound interest formula becomes
A = P e–rt.
Check Yourself 5
1.The population of a small town grows by 5% each year. The population is now 4570. What will the population be in 10 years’ time?
2.The number of bacteria in a certain colony doubles every 20 minutes. If the colony starts with a population of 800, how many bacteria will be present after 5 hours?
3.The half-life of radium is approximately 1600 years. How much of a 200-gram sample will be left after 100 years?
4.$2500 is invested at an interest rate of 15% compounded monthly. Find the new principal after 10 years.
Answers |
|
|
|
1. 7444 |
2. 100 218 |
3. approximately 192 g |
4. $11,101 |
Exponential and Logarithmic Functions |
139 |

The Number e
The history of mathematics is marked by the discovery of special numbers such as counting numbers, zero, negative numbers, and imaginary numbers. One of the most famous numbers of modern times is called e, or the Euler number.
John Napier, the inventor of logarithms, implied that this number existed in his work at the beginning of the seventeenth century. However, the Swiss mathematician Euler studied it more formally in the 1720s, and in 1727 he gave it the name e that we use today.
e is a real number constant that appears in different areas of mathematics. It is important in statistics for calculating the change in size of a population or quantity over time. It helps us to solve problems in probability and counting, and appears in the study of the distribution of prime numbers. We also use it to solve problems with logarithmic or exponential functions in calculus.
So how can we calculate this important number e?
One way is to define e as the number that the expression 1+ |
1 |
n approaches as n tends to infinity. |
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
The table below shows the value of this expression for different values of n. You |
|||||||||||||||
|
|
|
1 |
|
|
n |
||||||||||||||||
n |
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
can see from the table that as n gets larger and larger, the expression 1+ |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||
2 |
|
2.25 |
|
|
gets closer and closer to 2.71828..., which is the value of e. In fact, its value is |
|||||||||||||||||
5 |
2.48832 |
approximately 2.718 281 828 459 045 235 360 287 471. |
|
|
||||||||||||||||||
10 |
2.59374 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
100 |
2.70481 |
Alternatively, we can calculate the value of e using the following infinite sum: |
||||||||||||||||||||
1000 |
2.71692 |
|||||||||||||||||||||
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|
|
|
|
||||||||
10000 |
2.71815 |
e |
|
|
|
|
... . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
100000 |
2.71827 |
|
0 |
1 |
2 |
|
3 |
|
4 |
|
|
|
|
|||||||||
1000000 |
2.71828 |
Recently, mathematicians have discovered even more efficient ways of |
||||||||||||||||||||
1000000000 |
2.718281828 |
calculating e. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e is an irrational number, so its decimal expansion never terminates or completely repeats. Therefore, no matter how many digits in the expansion of e you know, the only way to find the next digit is to compute e using a particular method with more accuracy.
e is also a transcendental number, which means that e is not the root of any polynomial with rational number coefficients.
Finally, e is also the base of special types of logarithm known as natural logarithms. You will study natural logarithms later in this module.
140 |
Algebra 11 |

EXERCISES 3.1
A.Exponents
1.Evaluate the expressions.
a. |
9–1 |
|
|
|
b. |
3–2 |
|
|
||
|
1 |
–1 |
|
3 |
–2 |
|||||
c. |
(2) |
|
|
d. |
(2) |
|
||||
e. |
8 |
2–3 |
f. |
3 |
40 |
|||||
g. |
9 |
2–2 |
h. |
(9 |
3)–2 |
|||||
i. |
2–1 + 3–1 |
j. |
(3–2 + 2–2)–1 |
|||||||
k. |
2–1 + 4–1 + 8–1 |
l. |
|
34 |
( 3)5 |
|||||
|
3 5 |
( 3) 5 |
||||||||
|
|
|
|
|
|
|
|
|||
|
94 |
94 |
|
|
|
|
|
|
||
m. |
|
9 |
– 3 |
+1 |
|
|
|
|
|
|
141 |
94 |
|
|
|
|
|
||||
|
3 |
|
+3 |
|
|
|
|
|
|
|
2.Simplify each expression, given that all variables are positive. Leave each answer as a single expression with positive integer exponents.
a. |
a3 a5 |
b. (a–2)4 |
c. (x–2)–4 |
||||
d. ((x–2)–1)–3 |
e. (2p–3)–1 |
f. (–4x–3)–2 |
|||||
g. ((3x)–1)–2 |
h. 3(x2y)2 |
i. |
x5 |
||||
x3 |
|||||||
|
|
|
|
|
|
||
j. |
x2 |
k. |
x8 |
|
l. |
x–3 x–2 |
|
x5 |
x–3 |
x5 |
|||||
3. Evaluate each radical expression.
a. 12 27 4 27 |
b. 4 81 |
c. 3 64 |
4.Simplify each expression, given that all variables represent positive numbers.
a. |
4 81x12 |
y–8 |
b. |
3 x 4 x3 |
||||
d. |
6 |
1 |
|
e. |
|
x |
y + y |
x |
8x24 |
|
|
x + |
y |
||||
|
|
|
|
|
||||
5. Evaluate the expressions.
a. |
|
1 |
|
|
|
|
|
b. |
9– |
1 |
|
|
|
92 |
|
|
|
|
|
2 |
|
|
|
||||
d. |
16– |
3 |
|
|
|
e. |
|
1 |
|
|
|
||
4 |
|
|
|
–252 |
|
|
|
||||||
g. |
|
1 |
|
|
|
|
h. |
8– |
1 |
|
|
|
|
325 |
|
|
|
|
3 |
|
|
|
|||||
j. |
|
4 |
|
|
– 1 |
|
k. |
|
27 |
|
1 |
|
|
( |
|
|
) 2 |
|
(– |
8 |
)3 |
|
|||||
25 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
m. |
|
1 |
|
|
–3 |
|
1 |
n. |
|
2 |
|
– |
2 |
|
|
|
|
|
645 2 |
|
|||||||
(( 4) |
|
)12 |
|
5 |
|||||||||
c. 4 9x6
f. 3 –0.125x3y–15
3
c. 42
– 1
f. (–9) 2
1
i.(–8)3
1
l. (36–1 )2
11
o.32 272
6.Simplify each expression, given that all variables represent positive real numbers.
a. |
(243a5 )– |
1 |
b. |
1 |
|
c. |
(a4 a–8 )– |
1 |
|
5 |
(8m–6 )3 |
|
2 |
||||||
|
1 |
|
|
4 |
1 |
|
1 |
3 |
|
d. |
(9n–4 )2 |
|
e. |
2x3 4x– |
3 |
f. |
3x2 4x– |
2 |
|
Exponential and Logarithmic Functions |
141 |

7. Evaluate each expression.
|
|
2 |
|
|
– |
2 |
|
5 |
3 |
|
|
|
3 |
– 3 |
a. |
3 |
|
|
3 |
|
|
b. |
|
|
c. |
(4 |
|
|
) |
|
|
|
5– |
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
2 |
1 |
|
2 |
12 |
|
|
|
2 |
|
|
d. |
) |
2 |
e. |
f. |
(6 |
– |
|
|||||||
( |
|
|
|
|
|
48 |
|
) |
||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. Simplify the expressions.
a. |
|
ax+3 + ax+1 + ax–1 |
|
|
|||||||
|
ax–5 + ax–3 + ax–1 |
|
|||||||||
|
|
|
|||||||||
b. |
|
|
|
m |
+ |
|
|
m |
|
||
|
|
|
|
|
|
|
|||||
|
|
n n |
n |
– n |
|
||||||
|
( |
|
) +1 |
( |
|
) |
|
|
+1 |
||
|
m |
m |
|
|
|||||||
9.Evaluate the expressions for x , given that
2x + 2–x = 3.
a. 4x + 4–x |
b. 8x + 8–x |
B.Exponential Functions
10.Determine which functions are exponential functions.
a. f(x) = 53x c. f(x) = 3x–2 e. f(x) = xx
g. f(x) = (–2)x
b. f(x) = 4–2x d. f(x) = –2x f. f(x) = x2
11. Sketch the graph of each function.
x |
|
f (x)=( |
1 |
x |
a. f(x) = 3 |
b. |
3) |
|
|
c. f(x) = 5x |
d. |
f (x)=( |
1)x |
|
|
|
|
5 |
|
e. f(x) = 22x |
f. f(x) = 3–x |
|
||
12. In each case, find a function of the form f(x) = m ax which satisfies the conditions.
a.f(0) = 3 and f(2) = 12
b.f (1)= 23 and f(4)= 163
c.f –1(27) = 3 and f –1(81) = 4
13.Which number in each pair is greater?
a. |
3 |
7 |
|
|
|
|
|
b. |
|
4)10 |
|
21 |
||
44 , 48 |
|
|
|
|
|
( |
, (0.8) 2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
c. |
|
2 |
|
7 |
25 |
d. |
|
|
|
1 |
|
|
||
(0.7)3 , ( |
)36 |
( |
6) 6 , ( |
|
)0.6 |
|||||||||
10 |
|
|
||||||||||||
6 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
e. |
( |
2 1) 2+1, 5 ( |
2 1)12 |
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
25) 1 |
|
|
|
|
|||
f. |
x =( 5) |
3 1 |
, y= 5 ( |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
14. Determine whether each number is greater than 1.
|
|
|
|
|
|
1 |
|
2 |
|
5 27 |
12 |
a. |
( |
3) 5 |
3 |
b. |
( |
2 |
) |
|
c. |
5 3 5 |
|
d. |
(ñ5 – 2)ñ2 – 2 |
e. |
(ñ2 – 1)0.1 |
f. |
(ñ6 – 2)–2 |
|
|||||
142 |
Algebra 11 |
15. Determine whether each function is increasing () or decreasing ().
a. f(x) = 3x+1 |
b. f(x) = 21 – 2x |
|
|
|
||||
c. f(x) = 5 3x – 3 |
d. |
f (x)=( |
2)x |
+( |
3)x |
|||
|
|
|
|
3 |
|
|
|
5 |
e. f (x)= |
3x +5x |
f. |
f (x)=1 |
|
3 |
|
|
|
2x |
4x |
|
||||||
|
|
|
|
|
||||
16. For a 1 and x, y, z , show that if x + y 2z
then ax + ay 2az.
C. Simple Variations of Exponential Functions (Optional)
17.State the transformation(s) (i.e. the type of stretch, shrink or reflection) which should be applied to the graph y = 2x to obtain the graph of each function.
a. y = 2x + 1 |
b. y = 2x – 3 |
c. y = 2x – 2 |
d. y = 2x + 1 |
e. y = –2x |
f. y = 2–x |
1 |
|
g. y = 22 x |
h. y = 3 2x |
i. y = –2x – 2 |
j. y = 1 – 2x + 1 |
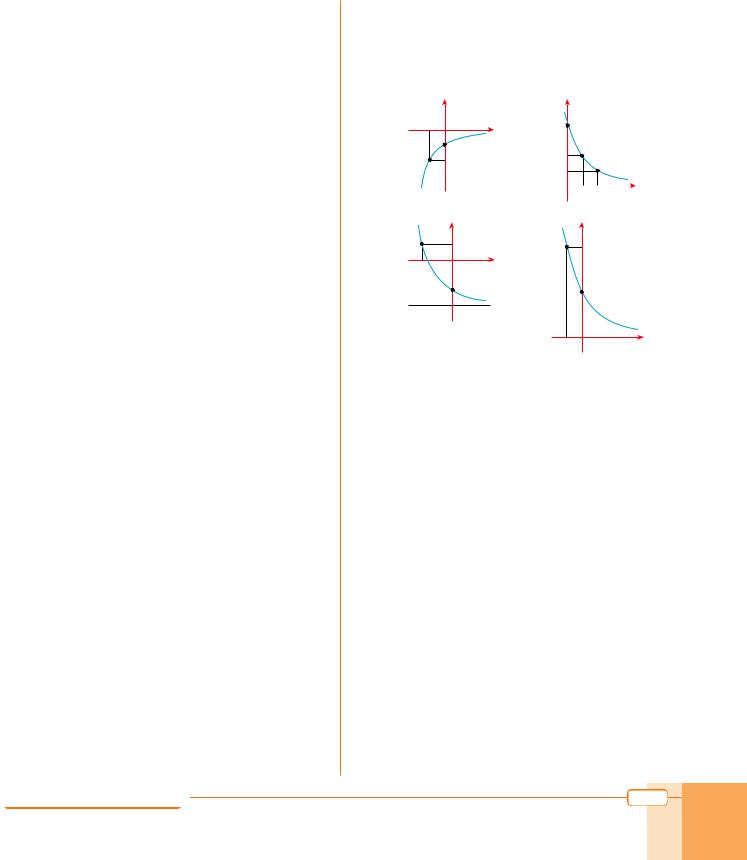
18.Each graph shows a single transformation of the graph f (x)=( 21)x. Write the equation of the new graph in each case.
a. |
y |
b. |
y |
|
–1 |
|
4 |
|
|
|
|
|
–1 |
x |
|
|
|
2 |
|
|
–2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 2 |
x |
|
c. |
y |
d. |
y |
|
1 |
|
6 |
|
–2 |
x |
|
|
–2 |
|
3 |
|
–3 |
|
|
–1 x
19.Determine the domain D, range R and asymptote a for each function.
a. y = 4 2x |
b. y = 3 2–x |
|||
|
x |
|
|
|
c. y = 2 |
|
+1 |
d. y = –5x |
|
2 |
|
|||
e. y = 2x – 3 |
f. y = 4+( |
1)x |
||
|
|
|
|
2 |
g. y = 6 – 3x |
h. y = –( 1)x |
|||
|
|
|
5 |
|
i. y = –e–x
Exponential and Logarithmic Functions |
143 |

20. Sketch each graph by plotting selected points.
a. y = 2x+ 3 |
b. |
y =(1)x – 2 |
||
|
|
3 |
|
|
1 x–2 |
|
|
x+2 |
|
c. y =(3) |
d. y = 10 |
|
|
|
e. y = 10x–3 – 3 |
f. |
y = –4+( |
1)x–1 |
|
|
|
|
|
2 |
g. y = –|5x| |
h. y = 2|x–1| |
|
||
i.y = 3 – (2 3x–2)
D. Applications of Exponential Functions
21.The number of bacteria in a growing colony is given by the function N(t) = 50 2t, where t is the time in hours.
a.How many bacteria were there initially?
b.How many bacteria will there be after 30 minutes?
c.How many bacteria will there be after 3 hours?
22.The population of a certain city was 450 000 in the year 2000 and is increasing with a relative growth rate of 8% per year.
a.Estimate the population in 2008.
b.Estimate the population in 2015.
23.A bacteria population doubles every ten minutes. If the population begins with one cell, how long will it take to grow to 1024 cells?
24.The number of bacteria in a colony is initially 39 and grows to 156 in 1 hour and 19 minutes. How many bacteria will be present 9 hours and 13 minutes after the initial measurement?
25.A new computer costs $1000. It is estimated that each year it will lose 9% of the previous year's value. Find the value of the machine after
a.the first year.
b.2 years.
c.12 years.
26.The half-life of a radioactive substance is 153 days. How many days will it take for 93.75% of a sample of the substance to decay?
27.The half-life of tritium is 12.4 years. How long will it take for 75% of a sample of tritium to decay?
28.An isotope of thorium, 327Th, has a half-life of 18.4 days. How long will it take for 87.5% of the sample to decay?
29.$1000 is invested with an interest rate of 10%, compounded monthly. Find the value of the investment after
a. 2 years. |
b. 4 years. |
c. 6 years. |
30.Find the principal required to obtain $600 interest after 2 years at 12% interest, compounded quarterly.
144 |
Algebra 11 |

A. LOGARITHMS
Consider the relation ax = N. Imagine that we are asked to find one of the three numbers a, x or N given the other two numbers. Three examples of this are shown below.
Case |
|
Solution |
Method |
|
25 |
= p |
32 |
raise 2 to the 5th power |
|
p3 |
= |
27 |
3 |
take the 3rd root of 27 |
3p = |
5 |
? |
? |
|
We can see that we cannot solve the last example with the algebra we have studied so far. We need to introduce a new concept: a logarithm.
|
|
1. Basic Concept |
||
|
|
The logarithm of a number N to a base a is the power to which a must be raised in order to |
||
|
|
obtain N. We write this as loga N. In other words, |
||
|
|
|
|
|
|
|
|
aloga N = N where ax = N and x = loga N. |
|
|
|
|
|
|
|
|
This equation is called the fundamental identity of logarithms. In this equation, the base of |
||
|
|
the logarithm (a) is always positive and different from 1, and the number whose logarithm is |
||
|
|
taken (N) is positive. In other words, negative numbers and zero do not have logarithms. |
||
|
|
|
||
Definition |
|
logarithm, argument, base, exponential form, logarithmic form |
||
|
||||
|
|
For a 0, a 1 and x 0, the real number y which is defined by |
||
|
|
y = log x ay = x |
||
|
|
a |
||
|
|
is called the logarithm of x to the base a. In this notation, x is called the argument of the |
||
|
|
logarithm. |
||
|
|
We say that the equation ay = x is in exponential form and loga x = y is the same equation |
||
|
|
in logarithmic form. |
||
EXAMPLE 28
Solution
Write the equalities in logarithmic form.
a. 23 = 8 |
b. 50 = 1 |
c. 3 2 = |
1 |
|
|
|
||
|
|
|
|
|
9 |
|
|
|
By the definition of a logarithm, ay = x y = log x. Therefore, |
|
|
|
|||||
|
|
|
a |
|
|
1 |
|
1. |
a. 23 = 8 3 = log |
8. |
b. |
50 = 1 0 = log |
1. |
c. 3 2 = |
–2 = log |
||
2 |
|
|
5 |
|
|
9 |
|
3 9 |
Exponential and Logarithmic Functions |
145 |

EXAMPLE 29
Solution
EXAMPLE 30
Solution
Write the equalities in exponential form.
a. log |
|
100 = 2 |
b. log |
|
1 |
= 3 |
c. |
log |
1 = 0 |
|
|
|
|
|||||
|
|
27 |
|
|
|
|
||||||||||||
|
|
10 |
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Again we use the definition loga x = y x = ay. |
|
|
|
|
|
|
|
|
|
|
||||||||
a. log |
|
100 = 2 100 = 102 |
|
|
b. |
log |
|
|
1 |
|
= 3 |
|
1 |
= 3 3 |
||||
10 |
|
|
3 |
27 |
|
27 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c. log2 1 = 0 1 = 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Solve each equation for x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a. logx 27 = 3 |
b. log4 |
x = 1 |
c. |
log4 16 = x |
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
a. |
logx 27 = 3 x3 |
= 27 x= 3 |
b. |
|
|
|
|
|
1 |
1 |
|
|
|
|||||
log4 |
x = |
42 |
= x x= 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
c. |
log4 16 = x 4x =16 4x = 42 x= 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
EXAMPLE 31
Solution
Remember:
ax = ay x = y
by the bijective property of exponential functions.
Calculate the logarithms. |
|
|
|
|
|
|
|
|||
a. log |
|
4 |
b. |
log |
|
1 |
c. log |
(log |
|
9) |
|
2 |
|
|
|
3 |
9 |
2 |
|
3 |
|
a.Let log2 4 = y.
Then log2 4 = y 2y = 4 2y = 22 y = 2, so log24 = 2.
b. Similarly, log3 91 = y 3y = 91 3y = 3–2 y= –2.
c.Let log3 9 = m. Then 3m = 9 3m = 32 m = 2. So we need to calculate log2 2. Starting with log2 2 = n, we get 2n = 2 which gives us n = 1. Thus, log2(log3 9) = 1.
|
32 Calculate the logarithms. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
EXAMPLE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
a. |
log |
3 |
1 |
|
|
b. |
log |
3 |
81 |
c. |
log |
3 a |
a |
|
d. log |
(log |
(log |
9 |
81)) |
||
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
a |
|
|
3 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Solution a. By the definition of a logarithm, we can write log |
3 |
1 |
= y 3y = |
1 |
3y = 3 1 |
y |
= 1. |
|||||||||||||||
|
|
|
|
|
|
1 = 1. |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
So log |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b. |
|
|
|
|
|
1)y |
|
1 |
1 |
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
log 1 |
3 81 = y ( |
=(81)3 |
3 y =(34)3 |
3 y = 3 3 |
y= |
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
146 |
Algebra 11 |

|
|
|
1 |
1 |
1 |
3 |
1 |
1 |
|
1. |
c. loga |
3 a |
a = y ay =(a a)3 |
ay =(a a2 )3 |
ay =(a2 )3 |
ay = a2 |
y= |
||||
|
|
|
|
|
|
|
|
|
|
2 |
So log a |
3 a a = |
1. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
d. Starting from the innermost logarithm, we have log9 81 = x 9x = 81 9x = 92 x = 2.
So we have to calculate log3 (log2 2), and log2 2 = y 2y = 2 y = 1. So the given expression becomes log3 1, which is equal to zero:
log3 1 = z 3z = 1 z = 0. In conclusion, log3(log2(log9 81)) = 0.
Notice that in these examples we were able to find the desired logarithm by writing the argument as a rational power of the base. This is not always possible, however: many logarithms (for example: log2 3 and log3 5) are irrational, and cannot be calculated in this way.
EXAMPLE 33 Evaluate the expressions.
a. 2log2 8 |
b. 25log5 3 |
c. 33 log3 2 |
|
Solution a. By the fundamental identity of logarithms, aloga N =N and so 2log2 |
8 will be equal to 8. |
||
However, let us try to evaluate the expression in a different way: |
|
||
Let log |
8 = t. Then we have to calculate 2t. |
|
|
2 |
|
|
|
By definition we have log 8 = t 2t = 8. So 2log2 8 = 8. |
|
||
|
2 |
|
|
b. Let log5 |
3 = t. Then we have to calculate 25t. By definition, log5 |
3 = t 5t = 3. So |
|
25t = (52)t = (5t)2 = (3)2 = 9, i.e. 25log5 3 |
= 9. |
|
|
(am)n = (an)m = am n |
|
|
|
c. In a similar way, let log 2 = t and let us calculate 33t. By definition, log 2 = t 3t = 2, |
|||
|
3 |
|
3 |
i.e. 33t = (3t)3 = 23 = 8. So 23 log3 2 = 8.
Check Yourself 6
1. Write the equalities in logarithmic form.
|
|
|
|
|
|
|
|
1 |
|||
a. 24 = 16 b. 103 = 1000 |
c. 30 = 1 d. 1253 = 5 |
||||||||||
2. Write the equalities in exponential form. |
|||||||||||
a. log |
|
|
0.01 = –2 |
b. log |
|
|
1 |
= 4 |
|||
10 |
1 |
16 |
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
d. log |
|
1 |
= 4 |
e. log |
|
|
32 = 5 |
||||
|
|
2 |
|||||||||
|
|
3 81 |
|
|
|
|
|||||
e. 3–3 = |
1 |
f. (2 2) |
2 |
|
1 |
|
3 |
= |
|||||
27 |
2 |
|||||
|
|
|
|
c. log10 10000 = 4
f. log 1 125 = 3
5
Exponential and Logarithmic Functions |
147 |

3. State whether each statement is true or false.
a. log3 729 = 6 |
|
b. |
log 1 |
3 4 = |
|
2 |
|
|
c. |
log10 |
|
|
1 |
= |
3 |
||||
|
3 |
|
|
10 |
10 |
2 |
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
d. log |
3 |
3 |
1 |
= |
3 |
e. |
loga |
a a |
|
a |
= |
7 |
(a > 0, |
a 1) |
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||
4. Determine the logarithms of each set of numbers to the given base.
|
a. 27, 1, 1, |
1 |
, |
3 9, |
|
9 |
|
to base 3 |
|
b. 2, 4, 1, |
1, |
1 |
, |
1 |
, 32, |
64 to base |
1 |
||
|
9 |
3 3 |
|
|
4 3 |
|
|
|
|
|
|
2 |
4 |
|
32 |
|
|
2 |
|
5. |
Solve for x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a. logx 4 = 2 |
|
|
b. |
|
log4 |
x = |
1 |
c. |
log25 125 = x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6. |
Calculate the logarithms. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a. log5 25 |
|
|
b. log6 1296 |
|
c. |
log49 |
1 |
|
|
|
d. log3(log2 (log2 256)) |
|||||||
|
|
|
|
7 |
|
|
|
||||||||||||
7. |
Evaluate the expressions. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
a. 3–log3 4 b. (2log2 5)2 |
c. 25–log5 10 |
d. |
492 log7 |
4 e. |
22log2 5+log2 3 |
|
|
|
|
|
||||||||
Answers
1. |
a. |
log2 16 = 4 |
|
|
|
|||
|
d. |
log125 |
5 = 1 |
|
|
|
||
|
|
|
|
|
3 |
|
|
|
2. |
a. |
10–2 = 0.01 |
|
|
|
|||
|
d. |
3–4 = |
1 |
|
|
|
|
|
|
81 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
3. |
a. |
true |
|
|
b. true |
|
||
4. |
a. |
3, 0, –2, |
– 1 |
, 2 |
, |
7 |
||
|
|
|
|
|
3 |
3 |
|
4 |
5. |
a. |
2 |
|
|
b. |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
6. |
a. |
2 |
|
|
b. |
4 |
|
|
7. |
a. |
1 |
|
|
b. |
25 |
|
|
|
|
4 |
|
|
|
|
|
|
b. log10 1000 = 3 |
c. log3 1 = 0 |
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
e. |
log3 |
|
= –3 |
f. |
log |
2 2 2 = – |
3 |
||||||
27 |
|||||||||||||
b. |
1 4 |
|
|
1 |
|
c. |
10 |
4 |
= 10000 |
|
|||
(2) = |
|
|
|
|
|||||||||
16 |
|
|
|
||||||||||
|
|
5 |
|
|
|
|
|
|
1 |
|
–3 |
|
|
e. |
2 |
|
= 32 |
|
|
f. (5) |
=125 |
|
|||||
c. true |
|
|
|
|
d. false |
e. |
true |
|
|
||||
b.–1, –2, 0, 1, 2, 5, –5, undefined
c.23
c. |
|
– |
1 |
d. |
1 |
|
|
|
|
|
2 |
|
|
|
|
c. |
|
|
1 |
d. |
1 |
e. 75 |
|
100 |
4 |
||||||
|
|
|
|||||
148 |
Algebra 11 |
