
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
9.7 Anwendungen |
381 |
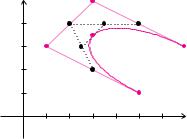
Bézier-Kurven sind für die Verwendung mit Computerprogrammen bestens geeignet. Beispielsweise lassen sich Kurvenpunkte mit dem Algorithmus von de Casteljau e zient und stabil berechnen. Dieser Algorithmus basiert auf der Rekursionsformel für BernsteinPolynome. Die grundlegende Idee besteht dabei in der gewichteten Mittelung zweier benachbarter Kontrollpunkte. Zur Berechnung des Kurvenpunktes für den Parameterwert t0 wird die Kante des Kontrollpolygons zwischen den Kontrollpunkten bk und bk+1 im Verhältnis t0 zu 1−t0 geteilt. Der einfachste Fall ergibt sich für t0 = 12 . Dann sind benachbarte Kontrollpunkte im Verhältnis 1 1 zu mitteln, siehe Beispiel 9.14.
Beispiel 9.14 (De Casteljau-Algorithmus)
Durch die vier Kontrollpunkte
b0 =Π|
5 |
‘ , b1 =Œ |
1 |
‘ , b2 =Œ |
3 |
‘ , b3 =Œ |
7 |
‘ |
1 |
3 |
5 |
3 |
wird eine Bézier-Kurve c(t) vom Grad 3 definiert. Den Kurvenpunkt zum Parameterwert t = 12 kann man konstruktiv ermitteln. Dazu bestimmt man die Mittelpunkte der Kanten des Kontrollpolygons b01, b12 und b23. Bei den beiden Verbindungskanten dieser Mittelpunkte bestimmt man wieder die Mittelpunkte b012 und b123. Der Mittelpunkt zwischen den Punkten b012 und b123 ist der Kurvenpunkt c( 12 ).
y |
|
b2 |
|
|
|
|
|
|
|
b123 |
|
b23 |
|
||
4 |
b12 |
|
|
||||
c ¡ |
21 ¢ |
|
|
b3 |
|||
3 |
b1 |
b012 |
|
|
|||
2 |
|
|
b01 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
b0 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
x |
Ì
9.7 Anwendungen
Kurven sind in der Anwendung sehr vielseitig. Im Grunde ist bei allen Dingen, die nicht ausschließlich geradlinig sind, in irgendeiner Form die Kurventheorie mit im Spiel. Ein klassisches Beispiel ist etwa die Bahnkurve eines Roboters. Die Kurve kann so festgelegt werden, dass sie zeitoptimal, energieoptimal oder weglängenoptimal ist. Wir greifen hier exemplarisch ein paar Anwendungen aus der Mechanik und dem Straßenbau heraus.
9.7.1 Mechanik
In der klassischen Mechanik treten Kurven häufig auf. Insbesondere lassen sich Bahnkurven von bewegten Objekten sehr gut mit Kurven beschreiben. Diese Kurven verlaufen sowohl in Ebenen als auch dreidimensional im Raum.
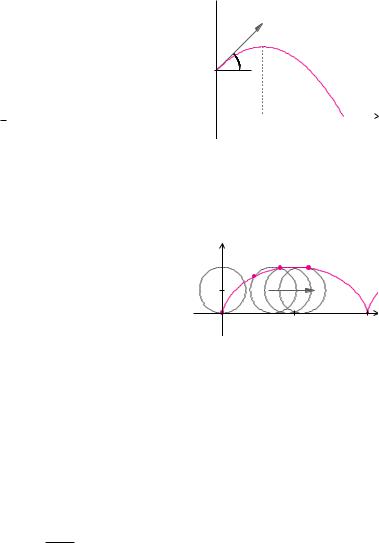
Beispiel 9.15 (Wurfparabel)
Ein Körper wird aus der Höhe h über dem Boden gemessen unter dem Winkel α geworfen. Die Geschwindigkeit hat den Betrag v0. Der Winkel α wird gegen die Horizontale gemessen. Wir bestimmen die Flugbahn in Abhängigkeit der Zeit. Dazu wählen wir das Koordinatensystem so, dass der Abwurfpunkt den x-Wert 0 und den y-Wert h hat. Wir erhalten für t [0, t1] die Parameterdarstellung
382 |
9 Kurven |
c |
t |
|
x t |
|
t v0 |
cos α |
|
21 g t2 |
|
h |
|
. |
) = Π|
y(t) |
‘ = Œ |
t v0 |
sin α |
− |
+ |
‘ |
|||||
|
( |
( ) |
|
|
|
|
|
Dabei bezeichnet die Konstante g ≈ 9.81 sm2 die Erdbeschleunigung. Der Parameterwert t1 bezeichnet die Flugdauer, er berechnet sich aus der Gleichung
t1 v0 sin α − 1 g t21 + h = 0.
2
y 
v0
c(t)
hα
x |
|
0 |
x |
|
1 |
x |
Mithilfe der Parameterelimination lässt sich die Kurve auch in Form einer Parabel darstellen: |
|
||||||||||||||||
t |
|
|
x |
y |
|
h |
tan α |
|
x |
|
g |
|
x |
2 |
. |
Ì |
|
|
v0 |
cos α |
|
|
|
|
2v02 cos2 |
α |
|
||||||||
|
= |
|
|
Ô |
|
= |
|
+ ( |
) |
|
− |
|
|
|
|
|
|
Beispiel |
9.16 (Zykloide) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Auf einer Kreisscheibe mit Radius r befindet sich im Abstand a vom Mittelpunkt ein exzentrischer Punkt P . Welche Bahnkurve beschreibt P , wenn wir die Scheibe horizontal abrollen lassen? Als Parameter der Bahnkurve wählen wir den Drehwinkel α:
c |
α |
|
x α |
|
r α |
a sin α |
|
. |
) = Π|
y(α) |
‘ = Œ |
r |
− a cos α |
‘ |
|||
( |
|
( ) |
|
− |
|
y |
|
c(α) |
|
r |
|
P |
|
πr |
2πr x |
Man kann die Gesamtbewegung des exzentrischen Punktes in die Bewegung des Mittelpunktes der Scheibe und die Bewegung des exzentrischen Punktes relativ zum Mittelpunkt zerlegen. Die beiden Koordinatenfunktionen x(α) und y(α) enthalten also eine translatorische und eine rotatorische Komponente. Ist a = r, liegt der exzentrische Punkt P also auf dem Rand der Kreisscheibe, so heißt die Zykloide gewöhnlich. Ist a < r, so nennt man die Zykloide gestreckt, ist a > r, so nennt man die Zykloide verschlungen. Eine gewöhnliche Zykloide hat wegen
x′(2π n) = r − r = 0, y′(2π n) = 0, n N0
an den Stellen α = 2πn einen singulären Punkt, genauer einen Umkehrpunkt. An diesen Stellen hat die Kurve eine senkrechte Tangente, denn für die Steigung gilt
|
lim |
m α |
|
|
lim |
y′ |
α |
|
lim |
|
|
a sin α |
|
|
lim |
cos α |
|
. |
|
||||
|
) = |
|
′( ) |
= |
|
− |
= |
|
|
= ±∞ |
|
||||||||||||
|
→ |
2πn |
( |
|
→ |
|
→ |
2πn r |
|
→ |
2πn sin α |
|
Ì |
||||||||||
α |
|
|
|
α |
|
2πn x |
(α) |
|
α |
|
a cos α |
α |
|
|
|
||||||||
9.7.2 Straßenbau
Keine Straße verläuft ewig geradeaus. So spielen Kurven bei der Trassierung von Straßen eine wichtige Rolle. Früher hat man bei der Straßenplanung viele Kurvenlineale mit unterschiedlichen Krümmungen für die Zeichnung der Pläne eingesetzt. Diese Utensilien sind heutzutage nicht mehr notwendig. Mit dem Computer lassen sich für den Anwender auf einfache Weise verschiedene Fahrbahnsegmente zusammensetzen. Hinter den Benutzeroberflächen verbirgt sich jedoch jede Menge interessante Mathematik.
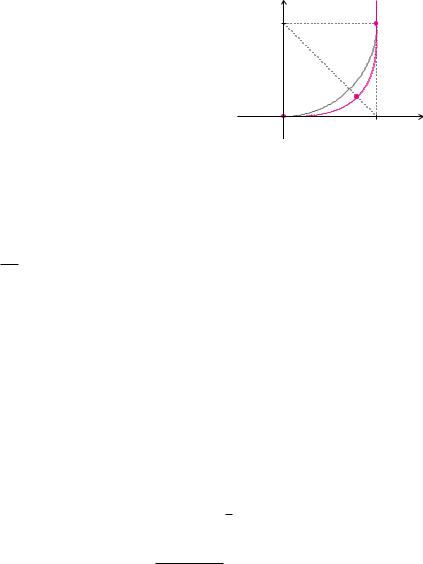
9.7 Anwendungen |
383 |
Straßen werden, soweit es die baulichen Gegebenheiten erlauben, so angelegt, dass sie möglichst sicher und komfortabel befahren werden können. Dazu fordert man insbesondere, dass der Lenkwinkel nicht sprunghaft geändert werden muss, um dem Straßenverlauf zu folgen. Dies hat auch einen Komfortaspekt, denn der Lenkwinkel und die Querbeschleunigung sind fahrdynamisch näherungsweise proportional. Man möchte also Unstetigkeiten in der Querbeschleunigung vermeiden.
Beispiel 9.17 (Klothoide)
Zwei Geradenstücke im 90○-Winkel sollen miteinander verbunden werden. Eine Lösung mit einem Kreisbogen mit Radius r hat den Nachteil, dass die Kurve an den Nahtstellen zwischen Geraden und Kreisbogen einen Sprung in der Krümmung besitzt. Besser ist der Ansatz mit einer Klothoide:
|
|
|
a√ |
|
|
t |
|
π2 |
2 |
|
|
||
c t |
x t |
|
π |
0 |
cos |
|
|
|
dτ . |
||||
|
|
’ |
|
|
|
S t |
|
τ |
|
|
|
“ |
|
|
y t |
|
|
|
π τ2 |
|
|||||||
( ) = Π|
( ) |
– a |
|
π |
0 |
sin |
|
|
|
|
dτ |
— |
|
|
|
|
|
|
|||||||||
|
( ) |
– |
|
√ |
S |
|
2 |
|
|
|
— |
||
|
|
” |
|
|
|
|
|
|
|
• |
|||
y |
|
r |
|
|
c(t) |
Kreis |
|
Klothoide |
|
r |
x |
Die Klothoide ist prinzipiell für alle t R definiert. Dabei ist a ein Parameter, der die Stärke der Krümmungsänderung beschreibt. Die Integranden besitzen zwar Stammfunktionen, diese sind aber nicht elementar darstellbar, siehe Abschnitt 7.3. Setzt man für die Klothoide die Formel für die Krümmung aus Definition 9.11 und die Formel für die Bogenlänge aus Definition 9.13 an, so erhält man nach einigen Rechenschritten
|
= |
√ |
|
|
= |
√ |
|
|
Ô |
|
= |
|
|
|
κ |
π t, s |
κ |
s. |
|||||||||||
|
||||||||||||||
|
||||||||||||||
|
|
|
a π t |
|
12 |
|||||||||
|
|
a |
|
|
|
|
|
|
a |
|
||||
Die Krümmung κ ist proportional zur Bogenlänge s. Die Klothoide besitzt also die richtige Eigenschaft für eine gleichmäßige Krümmungsänderung. Durchfährt man eine Klothoide mit konstanter Geschwindigkeit, so muss man den Lenkwinkel proportional zur Zeit ändern. Für das gesuchte Verbindungsstück zwischen den Geraden setzen wir also zwei Klothoidenbögen ein. Diese beiden Bögen sind symmetrisch zur Geraden r − x. Wir betrachten nun nur den einen Bogen, der am Anfang eine waagrechte Tangente hat. Für diesen Klothoidenbogen ist noch die Frage o en, wie der Parameterendwert t1 und der Kurvenparameter a gewählt werden müssen, damit die Kurve insgesamt ansatzfrei ist. Dazu bilden wir mithilfe des Hauptsatzes der Di erenzialund Integralrechnung, siehe Satz 7.1, den Tangentenvektor
c |
′ |
t |
x′ |
t |
|
( ) = Π|
y′ |
(t) |
|
|
|
|
( ) |
’ a√ |
|
cos |
πt2 |
“ |
|||||
π |
|||||||||
|
|
||||||||
‘ = – |
2 |
|
— |
||||||
– |
|
|
|
— |
|||||
|
|
2 |
|
||||||
– |
a |
π |
sin πt2 |
— |
|||||
” |
√ |
|
|
• |
|||||
|
|||||||||
und fordern, dass dieser am Endpunkt t1 den Winkel 45○ besitzt. Dazu muss der Sinuswert mit
√
dem Kosinuswert übereinstimmen. Wir erhalten t1 = 12 2. Weiterhin besteht die Bedingung, dass am Endpunkt des Kurvenbogens die Summe aus x-Wert und y-Wert gerade r ergeben muss:
r a(x(t1) + y(t1)) = r Ô a = .
x(t1) + y(t1)
Damit sind also sowohl t1 als auch a bestimmt. |
Ì |
