
Довідник
.docРозділ 1 Диференціальні рівняння першого порядку
1. Поняття диференціального рівняння і його розв`язку.
Рівняння, в яких невідома функція входить під знаком похідної або диференціала, називають диференціальними.
Якщо в диференціальному рівнянні невідома функція є функцією однієї змінної, то таке диференціальне рівняння називають звичайним.
Якщо невідома функція, яка входить у диференціальне рівняння, є функцією багатьох змінних, то таке диференціальне рівняння називають рівнянням з частинними похідними.
Загальний вигляд диференціального рівняння:
![]() .
.
Порядком диференціального рівняння називається найбільший порядок похідних, які входять в дане рівняння.
Розв`язком диференціального рівняння називається будь-яка функція, яка задовольняє цьому рівнянню (тобто функція, при підстановці якої в задане рівняння одержуємо тотожність).
При розв`язуванні диференціальних рівнянь слід враховувати, що розв`язок диференціального рівняння визначається неоднозначно, з точністю до постійної. Такий розв`язок називають загаль-ним розв`язком заданого рівняння.
Розв`язок, одержаний з використанням умови, де задані начальні дані називають частинним розв`язком заданого диференціального рівняння.
З геометричної точки зору множина всіх розв`язків диференціального рівняння є сім’я інтегральних кривих диференціального рівняння, а кожен частковий розв`язок є окрема інтегральна крива.
Задача знаходження частинного розв`язку диференціального рівняння, яке задовольняє заданим начальним умовам, зміст яких в том що у=у0 при х=х0, називається задачею Коші.
1. Диференціальні рівняння першого порядку.
Звичайним
диференціальним рівнянням першого
порядку називають рівняння вигляду
![]() або
або
![]() ,
окремий випадок
,
окремий випадок
![]() .
.
Задача Коші формулюється так: серед усіх розв`язків диференціального рівняння знайти такий розв`язок у=у(х), який при заданому значенні незалежної змінної х=х0 дорівнює заданому значення у0, тобто у(х0)=у0.
З геометричної точки зору знайти розв`язок
рівняння
![]() ,
що задовольняє початкову умову , у(х0)=у0
знайти
інтегральну криву цього рівняння, яка
проходить через задану точку (х,у0).
,
що задовольняє початкову умову , у(х0)=у0
знайти
інтегральну криву цього рівняння, яка
проходить через задану точку (х,у0).
Метод
розв`язування
рівняння вигляду
![]() :
:
якщо
функція f(x)
неперервна на деякому проміжку, то
розв`язком є функція
![]() .
.
Теорема
Пеано.
Якщо функція f(x,у)
неперервна в області D
площини хОу, то існує неперервна разом
із своєю похідною першого порядку
функція
![]() ,
яка є розв`язком диференціального
рівняння, що задовольняє початкову
умову
,
яка є розв`язком диференціального
рівняння, що задовольняє початкову
умову
![]() , де
, де
![]() .
.
На
геометричній мові теорему Пеано можна
сформулювати так. Якщо функція
![]() неперервна в області
неперервна в області
![]() площини
площини
![]() ,
то через кожну точку цієї області
проходить принаймні одна інтегральна
крива диференціального рівняння.
,
то через кожну точку цієї області
проходить принаймні одна інтегральна
крива диференціального рівняння.
2. Диференціальні рівняння першого порядку з відокремленими змінними
Диференціальне
рівняння виду
![]() називається диференціальним рівнянням
з відокремленими змінними.
називається диференціальним рівнянням
з відокремленими змінними.
Задача
Коші.
Якщо функція
![]() неперервна в інтервалі (a;b),
функція
неперервна в інтервалі (a;b),
функція
![]() і її похідна по у неперервна в інтервалі
(c;d),
тоді для будь-яких начальних даних
і її похідна по у неперервна в інтервалі
(c;d),
тоді для будь-яких начальних даних
![]() існує
єдиний розв`язок
існує
єдиний розв`язок
![]() рівняння
рівняння
![]() ,
який задовольняє умові
,
який задовольняє умові
![]()
Це рівняння може мати інший вигляд.
Рівняння
виду
![]() ,
де
,
де
![]() і
і
![]() - функції тільки від х,
а
- функції тільки від х,
а
![]() і
і
![]() - функції тільки від
у,
називається диференціаль-ним рівнянням
першого порядку з відокремленими
змінними.
- функції тільки від
у,
називається диференціаль-ним рівнянням
першого порядку з відокремленими
змінними.
Наведемо алгоритм розв’язування рівнянь цього типу:
1.
Розділити змінні.
Перенесемо в ліву частину вирази с
співмножником
![]() ,
а в праву -
з
,
а в праву -
з
![]() :
:
![]()
2.
Відокремимо
змінні
![]() .
.
3.
Проінтегруємо
почленно, знайдемо загальний розв’язок
рівняння:
![]() .
.
4.
З`ясувати,
чи має рівняння
![]() розв`язок,
який не отримано з загального інтегралу.
розв`язок,
який не отримано з загального інтегралу.
5. Розв’язавши задачу Коші, знайдемо частковий розв’язок.
3. Однорідні диференціальні рівняння першого порядку
Функція
![]() називається однорідною функцією
називається однорідною функцією
![]() -го
виміру, якщо при будь-якому
-го
виміру, якщо при будь-якому
![]() має місце тотожність
має місце тотожність
![]()
Диференціальне
рівняння першого порядку
![]() називають
однорідним, якщо
називають
однорідним, якщо
![]() є однорідною функцією нульового виміру.
є однорідною функцією нульового виміру.
Диференційне
рівняння першого порядку![]() називають однорідним, якщо його можна
представити у вигляді
називають однорідним, якщо його можна
представити у вигляді
![]() ,
де
,
де
![]() і
і
![]() -
однорідні функції однакового виміру.
-
однорідні функції однакового виміру.
Алгоритм розв’язання однорідних диференційних рівнянь
Однорідне
диференційне рівняння першого порядку
![]() зводиться до диференційного рівняння
з відокремлюваними змінними підстановкою
зводиться до диференційного рівняння
з відокремлюваними змінними підстановкою
![]() ,
де
,
де
![]() -
нова невідома функція. Тоді,
-
нова невідома функція. Тоді,
![]() .
.
-
Покладемо
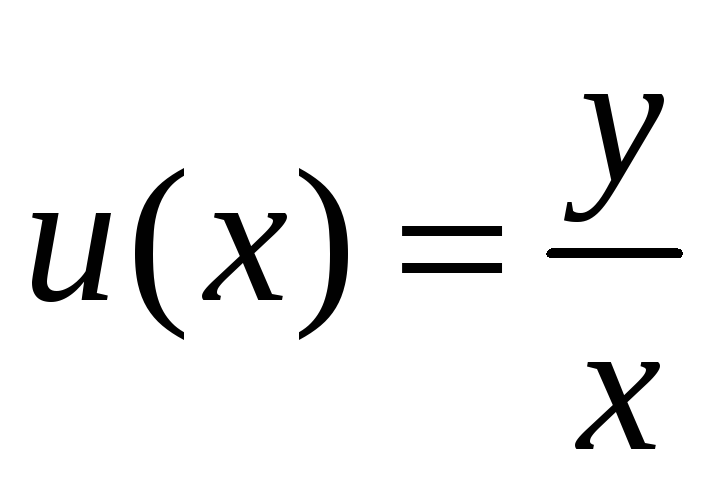 ,
тобто
,
тобто
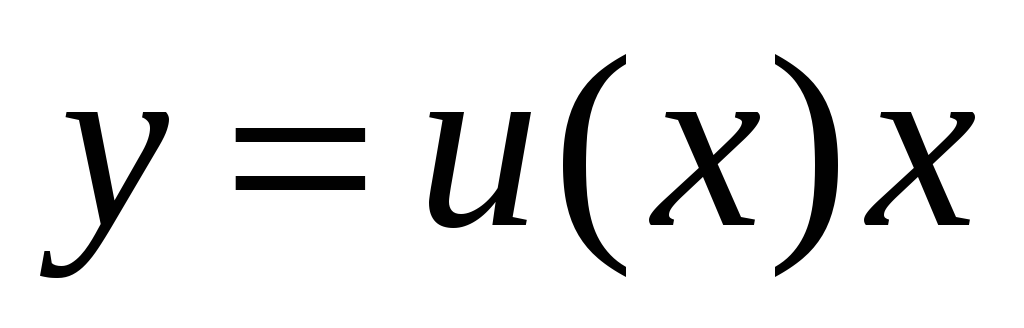 .
Тоді
.
Тоді
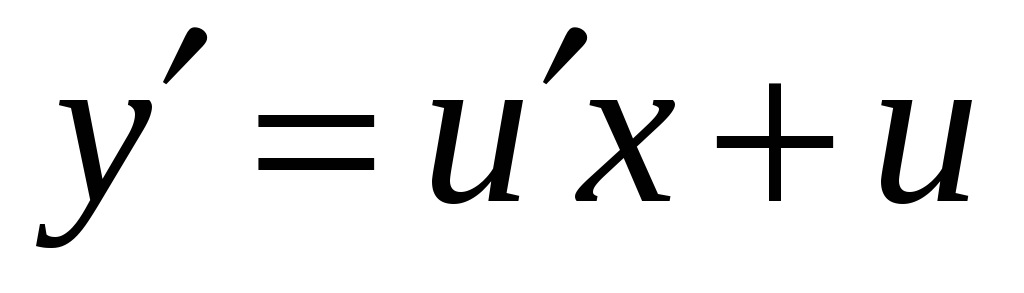 ,
і однорідне рівняння матиме вигляд:
,
і однорідне рівняння матиме вигляд:
 ,
або
,
або
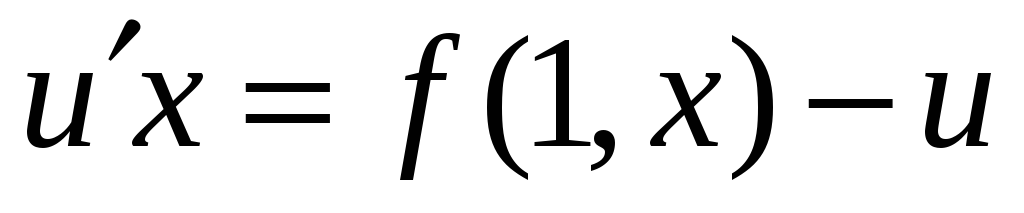 .
. -
Диференціальне рівняння допускає відокремлення змінних. Справді, якщо
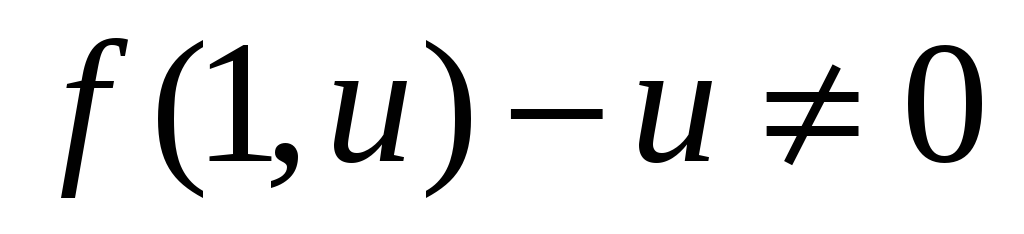 ,
то матимемо
,
то матимемо
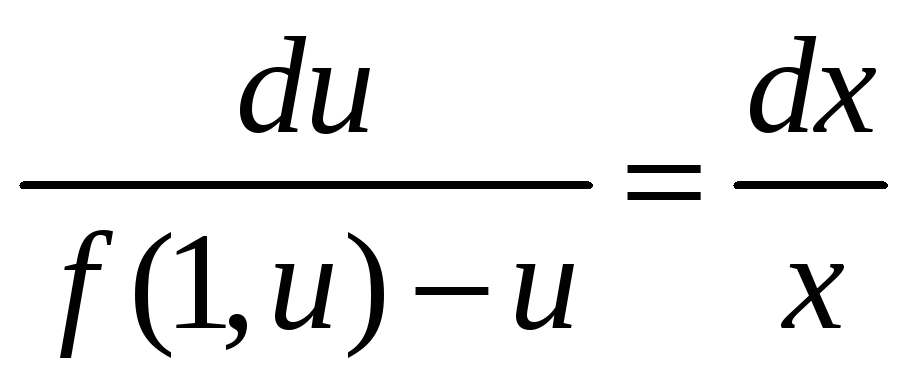 ,
звідси
,
звідси
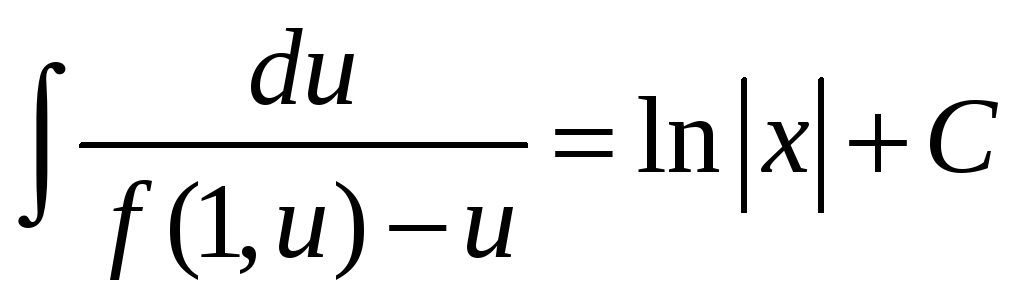 .
. -
Якщо
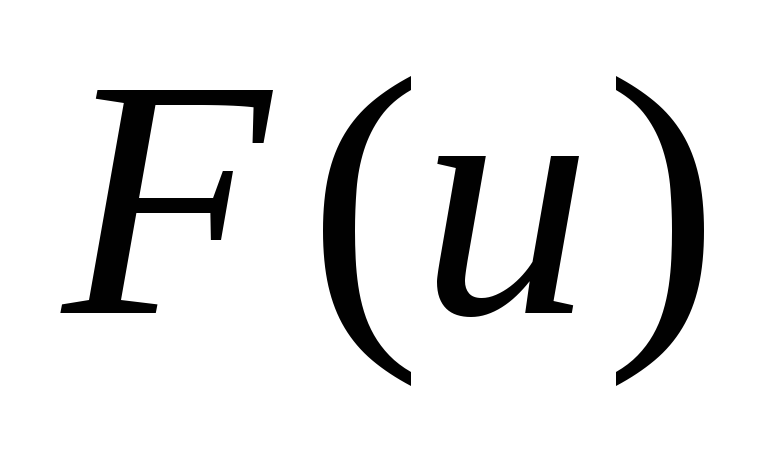 - деяка первісна підінтегральної
функції, то
- деяка первісна підінтегральної
функції, то є загальним розв’язком диференціального
рівняння.
є загальним розв’язком диференціального
рівняння.
Лінійні диференціальні рівняння І порядку.
Рівняння
вигляду
![]() ,
де
,
де
![]() і
і
![]() - деякі функції від х
називається лінійним диференціальним
рівнянням І порядку.
- деякі функції від х
називається лінійним диференціальним
рівнянням І порядку.
Якщо
![]() =0,
то рівняння прийме вигляд
=0,
то рівняння прийме вигляд
![]() називається однорідним і розв’язується
методом відокремлення змінних.
називається однорідним і розв’язується
методом відокремлення змінних.
Теорема
Коші. Нехай
![]() інтервал, в якому функції
інтервал, в якому функції
![]() та
та
![]() неперервні. Тоді: для будь-яких
неперервні. Тоді: для будь-яких
![]() та
та
![]() задача Коші с початковими значеннями
задача Коші с початковими значеннями
![]() має єдиний розв’язок, тобто існує єдине
рішення
має єдиний розв’язок, тобто існує єдине
рішення
![]() рівняння, яке задовольняє початковій
умові
рівняння, яке задовольняє початковій
умові
![]() .
.
Метод розв’язання диференційних рівнянь першого порядку:
Розв’язання
зводиться до рішення двох диференційних
рівнянь з відокремленими змінними за
допомогою підстановки
![]() ,
де
,
де
![]() та
та
![]() - невідомі функції від
- невідомі функції від
![]() ,
а
,
а
![]() .
.
Наведемо алгоритм розв’язання рівнянь такого типу:
-
Підставимо значення
 та
та
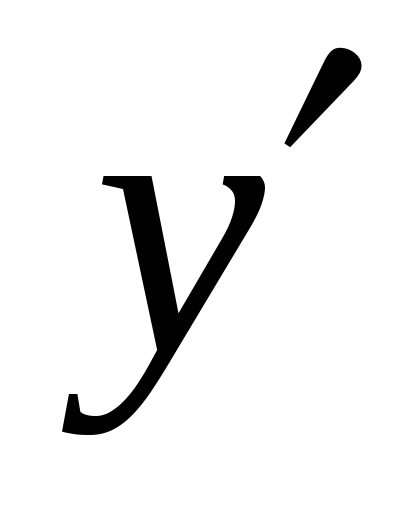 в рівняння та отримаємо
в рівняння та отримаємо

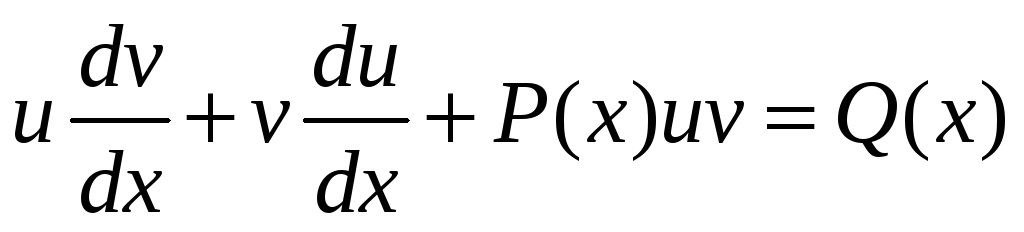 .
. -
Згрупуємо доданки, які мають однакову змінну
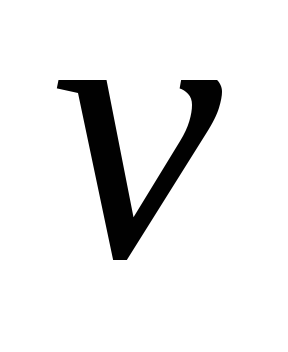 та винесемо її за дужки, тоді маємо
та винесемо її за дужки, тоді маємо
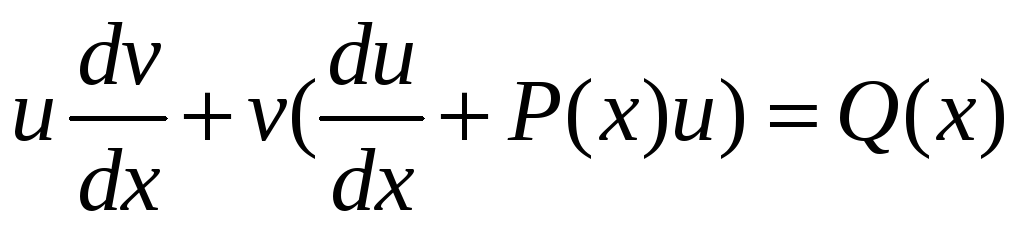
-
Виберемо функцію
 так, щоб
так, щоб
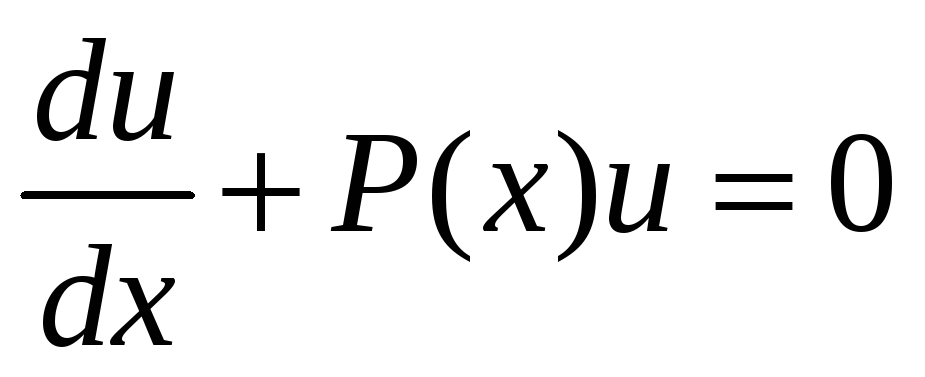 .
Розв’яжемо отримане рівняння і знайдемо
одне з частинних розв’язків функції
.
Розв’яжемо отримане рівняння і знайдемо
одне з частинних розв’язків функції
 .
. -
Підставимо знайдене значення функції
 в рівняння
в рівняння
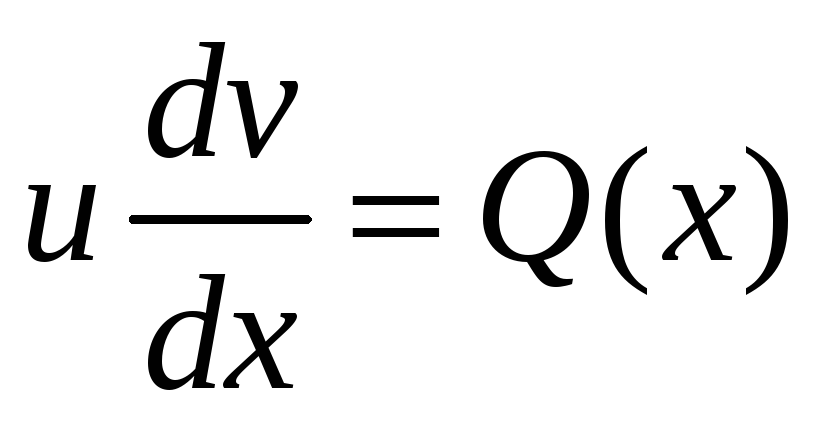 .
Отримаємо
.
Отримаємо
 .
. -
Розв’яжемо отримане рівняння, як рівняння з відокремлюваними змінними та знайдемо значення функції
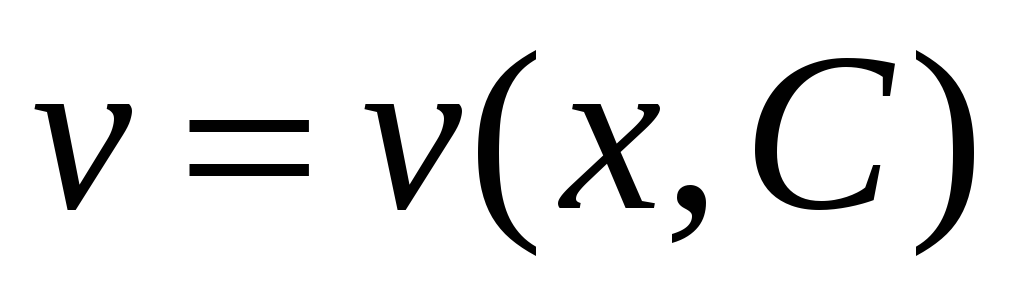 .
. -
Замінимо в рівнянні
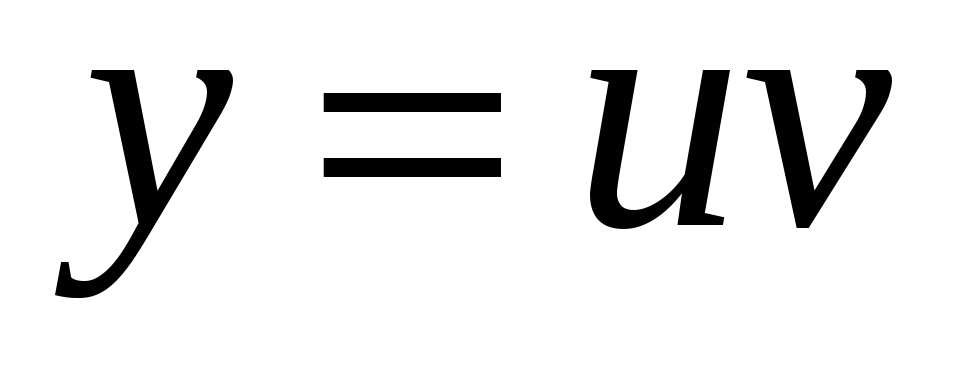 значення функцій
значення функцій
 і
і
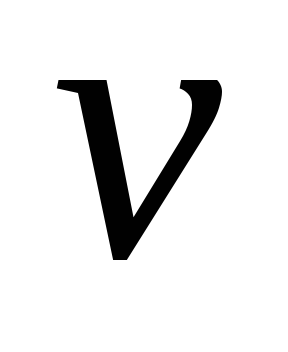 та отримаємо рішення
та отримаємо рішення
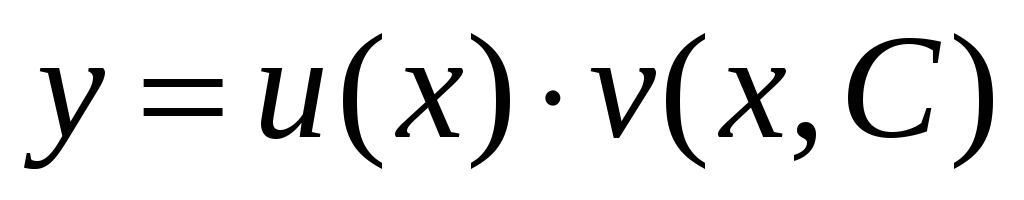 .
.
До
рівнянь, які зводяться до лінійних,
належить рівняння Бернуллі
![]() .
У ньому
.
У ньому
![]() та
та
![]() неперервні на проміжку
неперервні на проміжку
![]() ,
а
,
а
![]() -
деяке дійсне число.
-
деяке дійсне число.
Розділ 2 Диференціальні рівняння вищих порядків
Диференціальні рівняння ІІ порядку.
Якщо
диференціальне рівняння містить похідну
або диференціал другого порядку, то
воно називається диференціальним
рівнянням другого порядку
![]() .
Ми розглянемо
одне з рівнянь другого порядку
.
Ми розглянемо
одне з рівнянь другого порядку
Лінійні однорідні диференціальні рівняння ІІ порядку із сталими коефіцієнтами.
Рівняння вигляду
![]() ,
де
,
де
![]() і
і
![]() - деякі числа називається лінійними
диференціальними
рівняннями ІІ порядку зі сталими
коефіцієнтами. Якщо
- деякі числа називається лінійними
диференціальними
рівняннями ІІ порядку зі сталими
коефіцієнтами. Якщо
![]() ,
то диференціальне рівняння приймає
вигляд
,
то диференціальне рівняння приймає
вигляд
![]() і називається лінійним однорідним
диференціальним рівнянням ІІ порядку
зі сталими коефіцієнтами.
і називається лінійним однорідним
диференціальним рівнянням ІІ порядку
зі сталими коефіцієнтами.
В залежності від коренів характеристичного рівняння диференціальне рівняння має такі загальні розв’язки:
Складемо схему:
-
№
п/п
Корені рівняння
Загальний розв’язок
1.
D>0
Корені дійсні різні
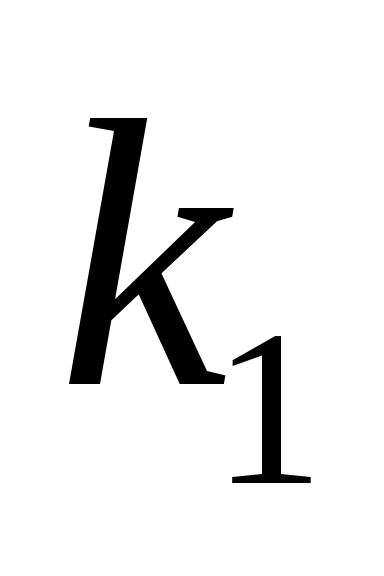 і
і
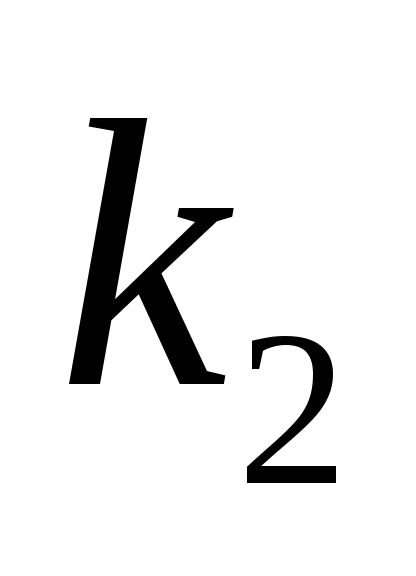
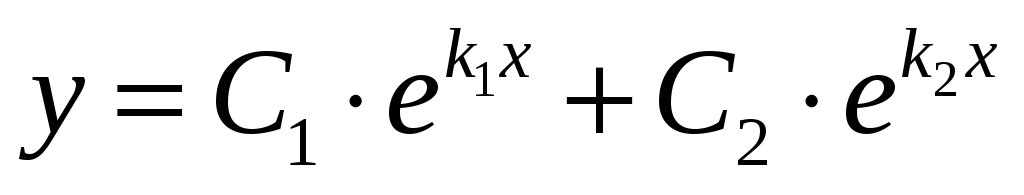
2.
D=0
Корені дійсні рівні
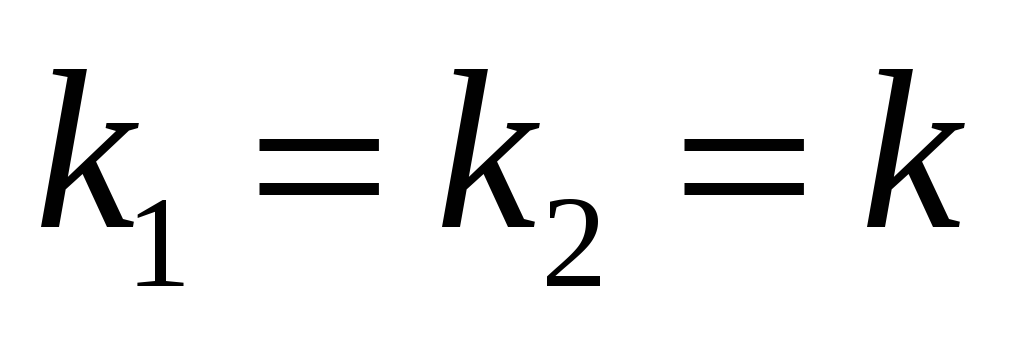
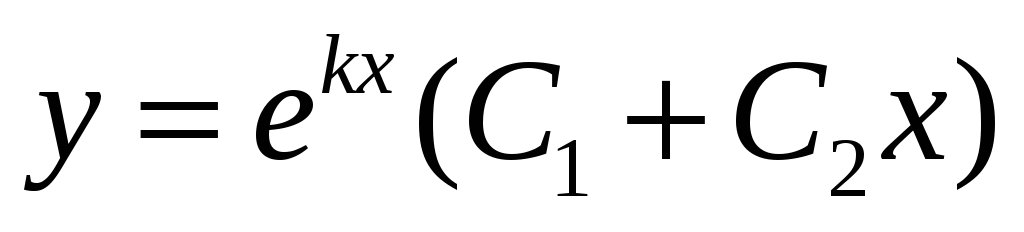
3.
D<0
Корені уявні різні
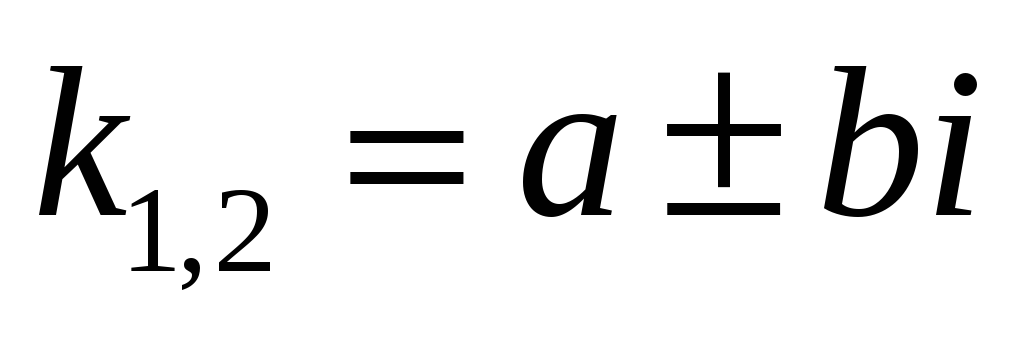

Рівняння
виду
![]() називається лінійним неоднорідним
диференціальним рівнянням ІІ порядку
зі сталими коефіцієнтами. Загальне його
рішення також можна записати у вигляді
суми уон
=
уоо
+ учн,
де
називається лінійним неоднорідним
диференціальним рівнянням ІІ порядку
зі сталими коефіцієнтами. Загальне його
рішення також можна записати у вигляді
суми уон
=
уоо
+ учн,
де
![]() -
загальне рішення однорідного рівняння,
учн
– частинне
рішення
неоднорідного
рівняння.
-
загальне рішення однорідного рівняння,
учн
– частинне
рішення
неоднорідного
рівняння.
учн можна знайти методом невизначених коефіцієнтів в наступних випадках:
-
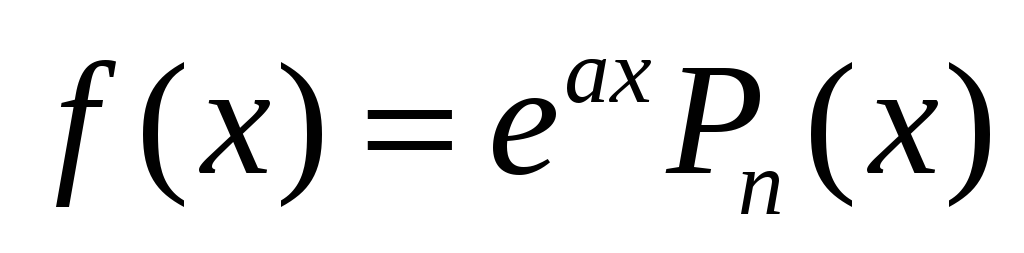 ,
де
,
де
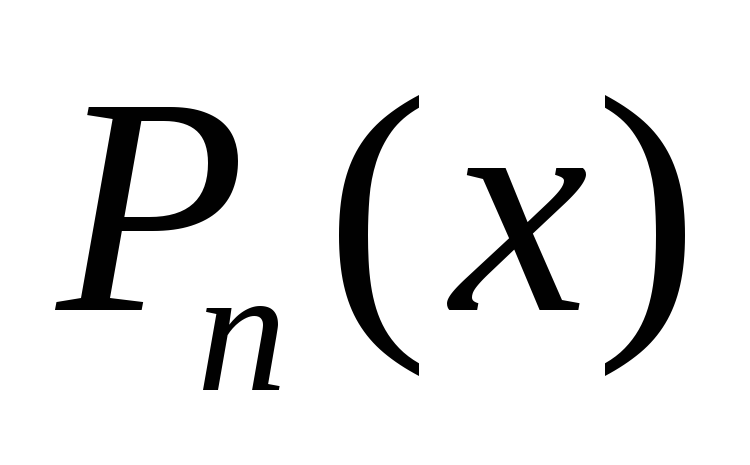 многочлен
ступеня
многочлен
ступеня
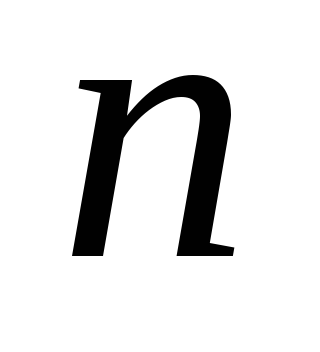 .
Якщо
.
Якщо
 не є коренем характеристичного рівняння,
тобто
не є коренем характеристичного рівняння,
тобто
 ,
то кладуть, що
,
то кладуть, що
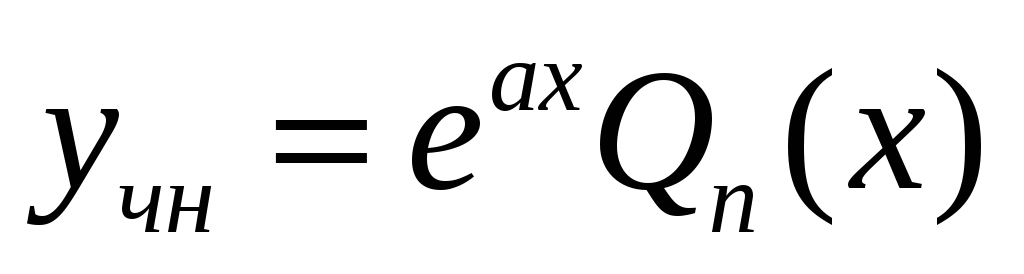 ,
де
,
де
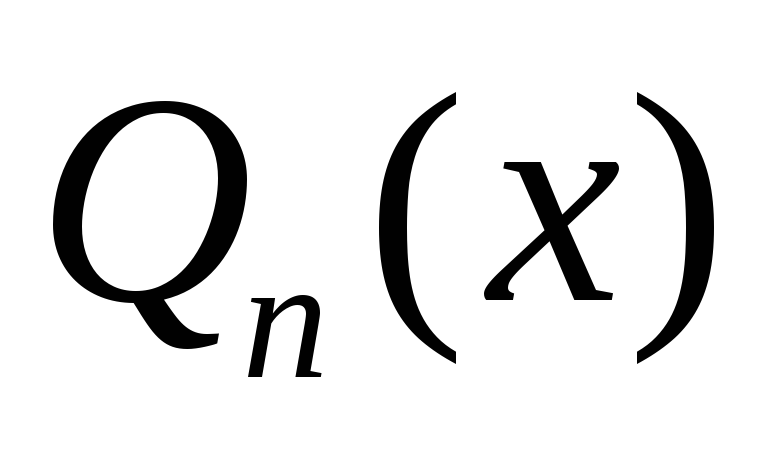 - многочлен ступеню
- многочлен ступеню
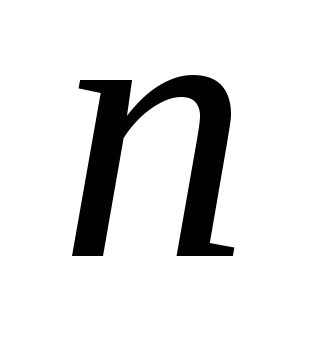 з невизначеними коефіцієнтами.
з невизначеними коефіцієнтами.
Якщо
![]() є коренем характеристичного рівняння,
тобто
є коренем характеристичного рівняння,
тобто
![]() ,
тоді
,
тоді
![]() ,
де
,
де
![]() - кратність кореня
- кратність кореня
![]() (
(![]() ,
або
,
або
![]() )
)
-
 .
Якщо
.
Якщо
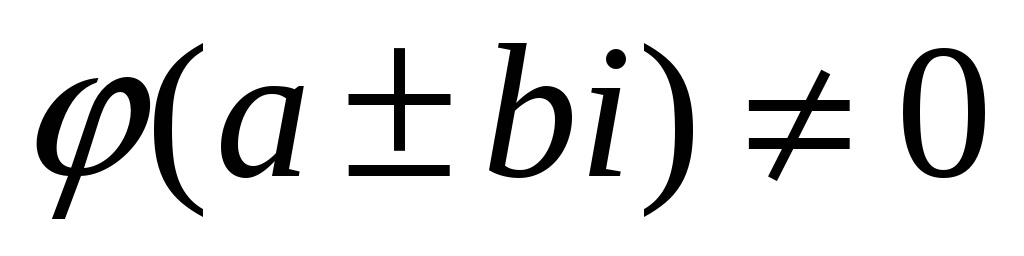 ,
то кладуть, що
,
то кладуть, що
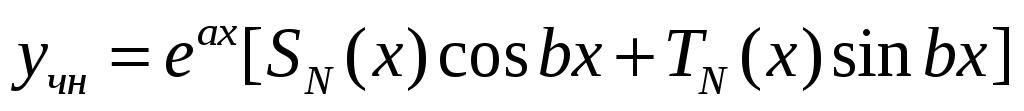 ,
де
,
де
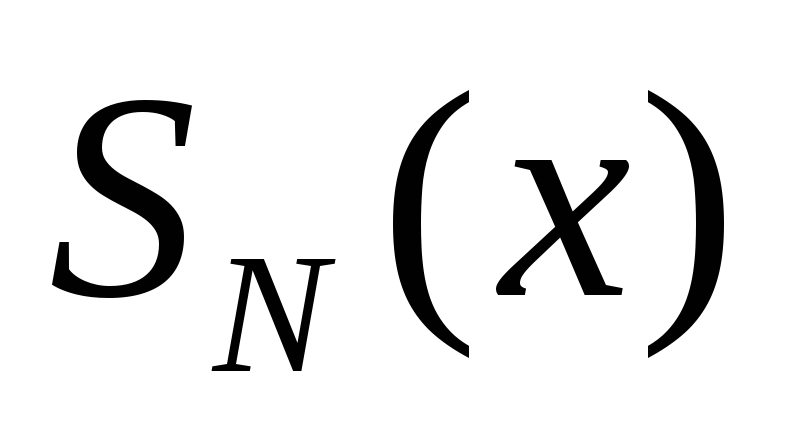 та
та
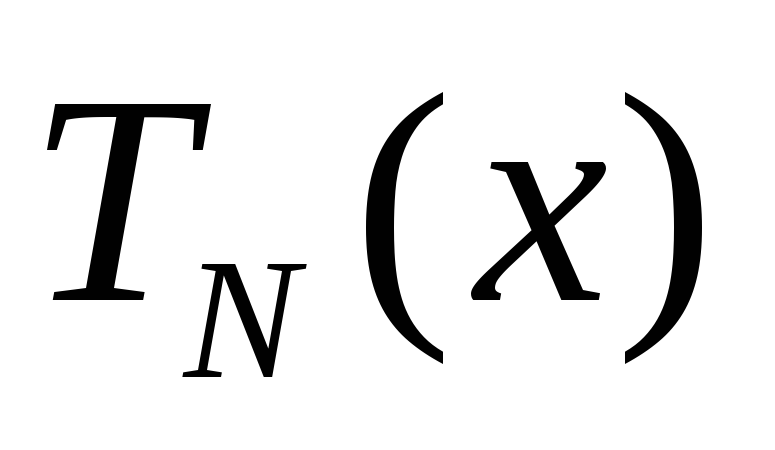 -
многочлени ступеню
-
многочлени ступеню
 .
Якщо ж
.
Якщо ж
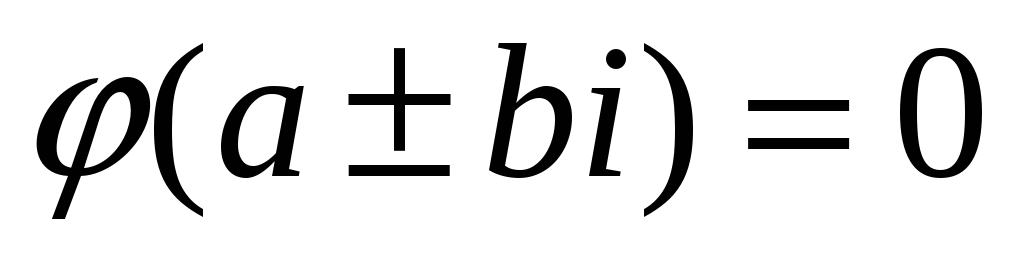 ,
то
,
то
 ,
де
,
де
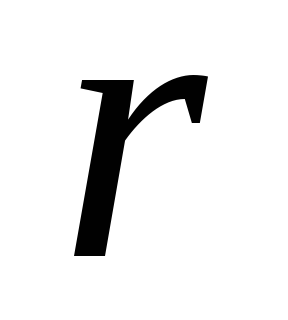 - кратність коренів
- кратність коренів
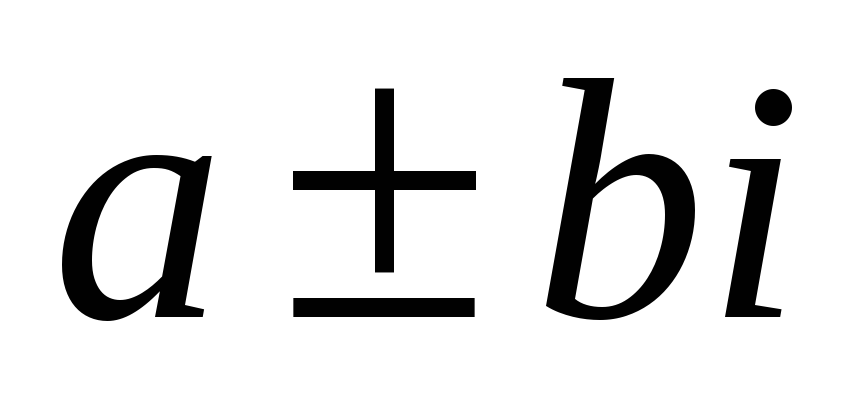 (для
рівнянь 2-го порядку
(для
рівнянь 2-го порядку
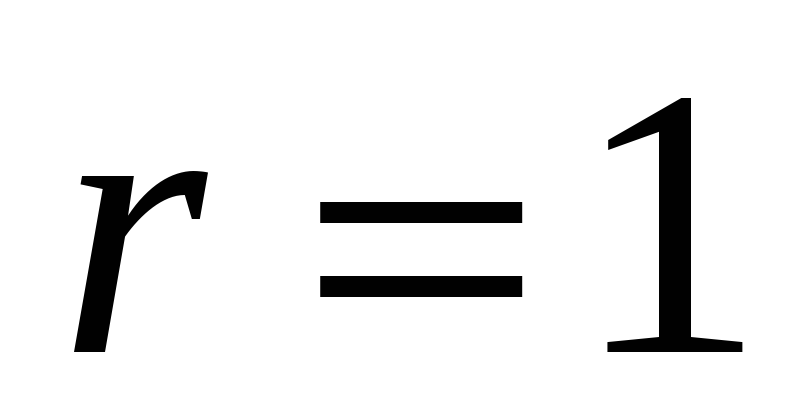 )
)
Розділ 3 Системи звичайних диференціальних рівнянь
