Часть3

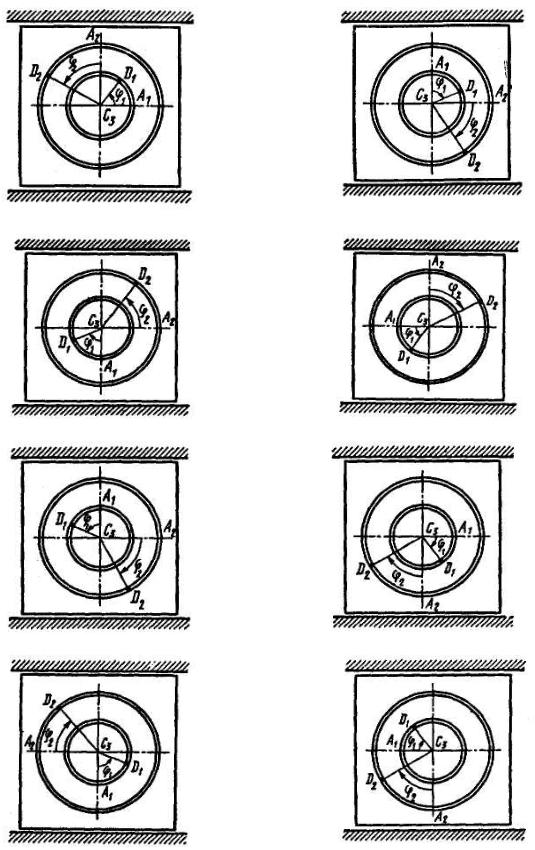
Рис. Д2.0

Рис. Д2.1

Рис. Д2.2

Рис. Д2.3

Рис. Д2.4

Рис. Д2.5

Рис. Д2.6

Рис. Д2.7

Рис. Д2.8

Рис. Д2.9

декартовы

координаты

которой равны xC =

åmk xk

,

yC =

åmk yk

,

M

M

åmk zk

zC =

, где xk , yk ,

zk – координаты точки системы,

mk

– масса точки,

M

M = åmk

– масса системы. Силы взаимодействия точек системы называются

силами;

они обозначаются

e . Свойства внутренних сил: главный

вектор

F

Ri = å

Fki = 0 , главный момент

Oi = åmO (

Fki ) = 0.

M

Дифференциальное уравнение движения центра масс системы в векторной форме

M aC = å

Fke ,

(1)

где M –

масса системы, aC – абсолютное ускорение центра масс системы,

å

Fke –

векторная сумма внешних сил, действующих на точки системы. По

a

=

dVC

= 0

= const ; это означает,

C

и, следовательно, V

что центр масс

dt

C

системы движется прямолинейно и равномерно.

б) Записав уравнение (1) в проекции на ось, получим

MaCx

= åFkxe .

(2)

Частный случай: если выполнены одновременно два условия

xC = const

åFkxe = 0 и VCx = 0 при t = 0,

то

– координата xC центра масс системы остается постоянной и

равной своему начальному значению

xC (t) = xС (0) ,

Пример Д2. Механическая система

состоит из грузов D1 массой m1 и D2

массой m2 и из прямоугольной

вертикальной плиты массой m3,

движущейся вдоль

горизонтальных

направляющих (рис. Д2). В момент

времени

t0=0,

когда

система

находилась в покое, под действием

внутренних

сил

грузы начинают

двигаться по желобам, представ-

ляющим собой окружности радиусов r

Рис. Д2

и R, по законам ϕ1 = f1 (t) и ϕ2

= f2 (t) .

Дано: m1 = 6 кг, m2 = 8

кг, m3 = 12 кг, r = 0,6 м, R = 1,2 м,

ϕ1 = πt ,

ϕ2

=

π (1− t) (t – в секундах).

2

Определить: x3 = f3 (t)

– закон движения

плиты,

N = f (t)

– закон

направляющих

N

. Запишем уравнение движения центра

масс системы в

векторной форме:

M aC =

(1)

P1 + P2 + P3 + N .

определения x3 = f3 (t) спроектируем уравнение (1) на ось x. Получим

&&

e

&&

(2)

M xC

= åFkx

или M xC = 0,

так как все внешние силы перпендикулярны оси x и поэтому åFkxe = 0 .

Отметим также, что VCx = 0

при t = 0. Поэтому, интегрируя дважды уравнение

(2), получим:

M xC = const

(3)

(закон сохранения координаты центра масс системы). Из (3) следует, что

M xC (t) = M xC (0) .

(4)

Определим значение

M xC (t).

Координата xC центра масс

системы

определяется по формуле

M xC = m1x1 + m2 x2 + m3 x3 .

(5)

формулу (5) и учитывая заданные зависимости ϕ1 и ϕ2 от t, получим

M xC (t) = (m1 + m2 + m3 )x3 (t) − m1R cos(πt) + m2r sin(π 2 − πt 2).

(6)

Определим значение M xC (0) . Подставляя в (6) t=0, x3(0)=0, получим

M xC (0) = −m1R + m2r .

(7)

N = f (t)

спроектируем векторное уравнение (1)

на вертикальную ось y (см.

рис. Д2):

e

&&

&&

(8)

M yC

= åFky

или MyC = N − P1 − P2 − P3 .

Отсюда получим, учитывая, что P1=m1g, и т.д.:

(9)

N = M yC + (m1 + m2 + m3 )g ,

где yC

&&

определим сначала

yC (t).

пока неизвестно. Для

нахождения yC

&&

&&

Координата yC центра масс системы определяется по формуле

M yC = m1 y1 + m2 y2 + m3 y3 .

(10)