1. Математическим описанием связей между событиями занимается алгебра событий. Алгебру событий называют алгеброй Буля по имени английского математика Дж. Буля (1815–1864).

Для того чтобы понять смысл вероятности, напомним некоторые понятия теории множеств и операции над множествами.

Множество – это совокупность, набор, коллекция, собрание каких-либо элементов, объединенных по определенному признаку. Число элементов в множестве может быть конечным и бесконечным (например, все числа, лежащие между 0 и 1).

Полное множество Х – набор, содержащий все элементы в заданном контексте.

Пустое множество Ø – набор, не содержащий элементов. Всякое подмножество X есть множество (например, множество А, Ā и Ø). Задав набор А, можно определить его дополнение. Дополнением Ā множества А является набор, содержащий все элементы из полного набора X, которые не являются элементами набора А.

Диаграммы Венна, названные по имени английского логика Дж. Венна, наглядно представляют операции множеств и связанные с ними соотношения. На диаграммах Венна множество обозначается кругом, эллипсом или другой геометрической фигурой внутри прямоугольника, обозначающего полное множество.

Взаимоотношение между набором А и его дополнением показано на рис. 1.1, а.

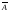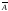Пример 1.1. Пусть полный набор – все студенты института. Определим А – множество студентов, сдавших летнюю сессию только на «отлично». Дополнение А есть – множество студентов неотличников. В сумме А и – все студенты института.

Рассмотрим подмножества А и В внутри полного множества X. Определим пересечение А и В.

Пересечение А и В (обозначается как А∩В) есть набор, содержащий все элементы, которые являются членами и А и В (см. рис. 1.1, б).

Объединение А и В (обозначается АВ) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе (см. рис. 1.1, в).

Продолжим рассмотрение примера со студентами. Определим В как множество студентов, сдавших зимнюю сессию на «отлично». Тогда пересечение А и В – подмножество студентов, сдавших на «отлично» и летнюю, и зимнюю сессии.

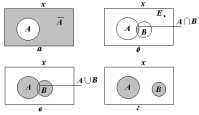
Объединение А и В – подмножество студентов, которые сдали на «отлично» или летнюю, или зимнюю, или обе сессии.

Два набора могут не иметь пересечения. В этом случае мы говорим, что пересечение А и В есть пустое множество (см. рис. 1.1, г). В примере с успеваемостью студентов подмножество студентов, получивших двойки в летнюю сессию, не пересекается с подмножеством отличников.

                       

Теория вероятностей изучает случайные события. Случайным событием называется событие, которое может произойти или не произойти в результате некоторого эксперимента (далее будем опускать термин «случайный»).

Событие – это любое подмножество пространства событий, набор элементарных исходов. В диаграммах Венна событию соответствует подмножество элементарных событий. Событие произошло, если в результате эксперимента произошло элементарное событие, принадлежащее этому поднабору. Например, элементарные события – «туз конкретной масти» – благоприятствуют случайному событию «туз».

События обычно обозначаются заглавными буквами латинского алфавита: А, В, С, D, Е, F и т. д. События можно классифицировать.

Достоверное событие – это событие, которое обязательно произойдет в результате испытания (подброшенный камень обязательно упадет на Землю вследствие действия закона притяжения). Достоверные события условимся обозначать символом Ω.

Невозможное событие – это событие, которое не может произойти в результате данного опыта (извлечение черного шара из урны с белыми шарами есть событие невозможное). Невозможное событие обозначим Ø.

Достоверные и невозможные события не являются случайными.

Совместные события – несколько событий называют совместными, если в результате эксперимента наступление одного из них не исключает появления других. (в магазин вошел покупатель. События «в магазин вошел покупатель старше 60 лет» и «в магазин вошла женщина» – совместные, так как в магазин может войти женщина старше 60 лет.)

Несовместные события – несколько событий называют несовместными в данном опыте, если появление одного из них исключает появление других (выигрыш, ничейный исход и проигрыш при игре в шахматы как результат одной партии – три несовместных события).

События называют единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет. Некоторая фирма рекламирует свой товар по радио и в газете. Обязательно произойдет одно и только одно из следующих событий: «потребитель услышал о товаре по радио», «потребитель прочитал о товаре в газете», «потребитель получил информацию о товаре по радио и из газеты», «потребитель не слышал о товаре по радио и не читал газеты». Это четыре единственно возможных события.

Несколько событий называют равновозможными, если в результате испытания ни одно из них не имеет объективно большей возможности появления, чем другие (при бросании игральной кости выпадение каждой из ее граней – события равновозможные).

Два единственно возможных и несовместных события называются противоположными (купля и продажа определенного вида товара есть события противоположные).

Полная группа событий – совокупность всех единственно возможных и несовместных событий.

2.ОПРЕДЕЛЕНИЕ(классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1

Свойство 2. Вероятность невозможного события равна нулю.

В этом случае m=0, следовательно, P(A)=m/n=0/n=0

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,

0<P(A)<1

Итак, вероятность любого события удовлетворяет двойному неравенству

0 P(A)1

Свойства вероятности, вытекающие из классического определения:

1. Вероятность достоверного события равна 1, т. е. Р(Ω) = 1. Действительно, если событие А = Ω, то М = N, значит, P(Ω) = 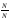=1.

2. Если событие невозможное, то его вероятность равна 0, т.е. Р(Ø) = 0. Если А = Ø, то оно не осуществится ни при одном испытании, т. е. М = 0 и Р(Ø) = 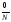= 0.

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1. В самом деле, так как 0 ≤ М ≤ N, то 0 ≤ М / / 0 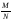≤ 1, т. е. 0 ≤ P(A) ≤ 1.

4. Сумма вероятностей противоположных событий равна 1, т. е.

Р(А) + Р(Ā) = 1, Р(Ā) = (N – M) / N = 1 – M/N = 1– Р(А),

а отсюда

Р(А) + Р(Ā) = 1.

3. Другой тип вероятности определяется исходя из относительной частоты (частости) появления события. Если, к примеру, некоторая фирма в течение определенного времени провела опрос 1000 покупателей о новом сорте напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток, как 20/1000 = 0,02. В этом примере 20 – частота наступления события, а 20/1000 = 0,02 – относительная частота.

Относительная частота события – отношение числа испытаний т, при которых событие появилось, к общему числу проведенных испытаний п:

ω(A) = 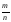, (1.2)

где m – целое неотрицательное число; 0 ≤ m ≤ п.

Чем же отличается относительная частота от вероятности? Относительная частота – результат многократных испытаний. С увеличением числа испытаний относительная частота проявляет тенденцию стабилизироваться, проявляет устойчивость, а именно приближается с затухающими отклонениями к постоянному числу, называемому статистической вероятностью. В качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.

Статистической вероятностью события А называется относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний.

4. Теорема сложения вероятностей. Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

P(A + B) = P(A) + P(B) – P(AB)

или P(A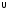B) + P(A) + P(B) – P(A∩B). (1.5)

Сумму событий А + В называют событием, состоящим в появлении события А, или события В, или обоих событий А и В.

Смысл правила (1.5) очень прост и понятен интуитивно: когда мы складываем вероятности событий А, В, то измеряем, или взвешиваем, вероятность их пересечения дважды – первый раз, когда измеряем относительный размер события А внутри пространства событий, и еще раз, когда делаем то же самое с событием В. Отсюда, поскольку относительный размер, или вероятность пересечения двух наборов, взвешивается дважды, мы вычитаем одно из них и, следовательно, получаем истинную вероятность объединения двух событий.

5. События А и В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие.

События А и В называются зависимыми, если вероятность каждого из них зависит от того, произошло или нет другое событие.

■ Теорема умножения вероятностей. Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого:

Р(А·В) = Р(А∩В) = Р(В)∙Р(А/В) = Р(A)∙Р(B/A). (1.8)

Произведением событий А и В называют событие, состоящее в одновременном появлении и события А, и события В.

Доказательство. Проиллюстрируем понятие условной вероятности для случая равновозможных элементарных исходов, где применимо классическое определение вероятности. Пусть даны два события А, В, такие, что Р(А) ≠ 0 и P(B) ≠ 0, и пусть из всех возможных N исходов событию А благоприятствуют М исходов, событию В благоприятствуют К исходов, событию А и В благоприятствуют L исходов. Вероятности событий А, В, А·В соответственно равны Р(А) = M/N, Р(В) = K/N, Р(А·В) = L/N.

Подсчитаем условную вероятность события В/А. Событию В/А будут благоприятствовать L исходов из М исходов. Тогда Р(В/А) = = L/M. Разделим числитель и знаменатель дроби на N и получим

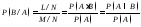, (1.9)

где Р(А) ≠ 0.

Вероятность наступления события В, вычисленная при усло­вии, что событие А уже произошло, равна вероятности пересечения событий А и В, деленной на вероятность события А. Из формулы (1.10) следует (1.9).

8. Итак, в выборочном социологическом исследовании случайная величина предстает перед социологом в виде признака, для каждого значения которого (а таких значений – конечное количество) известна относительная частота его встречаемости. Эта частота интерпретируется как выборочная оценка соответствующей вероятности (вопрос о правомерности такой трактовки не прост; здесь мы его не рассматриваем; см. п.4.1 части I). Совокупность частот встречаемости всех значений признака, соответственно, трактуется как выборочное представление функции плотности того распределения вероятностей, которое и задает изучаемую случайную величину. Подчеркнем, что пока речь идет об одномерной случайной величине (ниже, переходя к оценке вероятностей встречаемости сочетаний значений разных признаков, мы тем самым перейдем к многомерным случайным величинам).

Пусть, например, вопрос в используемой социологом анкете звучит: “Какова Ваша профессия ?” и сопровождается 5-ю вариантами ответов, закодированных числами от 1 до 5. Тогда частотное распределение - аналог функции плотности - будет иметь, например, вид:

Таблица 1.

Пример одномерной частотной таблицы

Значение признака	1	2	3	4	5
Частота встречаемости (%)	20	15	25	10	30

Вместо процентов могут фигурировать доли: 20% заменится на 0,2, 15 - на 0,15 и т.д. (в случае такой замены мы получим числа, конечно, в большей степени похожие на вероятности, поскольку величина вероятности, как известно, изменяется от 0 до 1).

То же частотное распределение можно выразить по-другому, в виде диаграммы вида, отраженного на рис. 1 или в виде т.н. полигона распределения, рис.2.

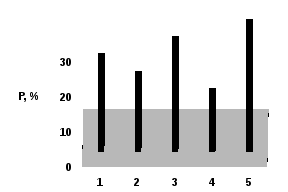
Рис.1. Диаграмма распределения, рассчитанная на основе таблицы 1.

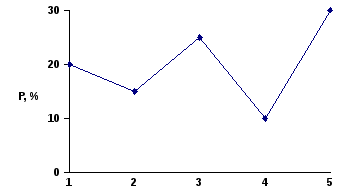
Рис. 2. Полигон распределения, рассчитанный на основе таблицы 1.

В социологической практике интервальность шкалы обычно сопрягается с ее непрерывностью, т.е. с предположением о том, что в качестве значения интервального признака в принципе может выступить любое действительное число, любая точка числовой оси.

Переходя к описанию выборочного представления функции распределения или функции плотности распределения, прежде всего отметим, что непрерывную кривую в выборочном исследовании нельзя получить никогда. Здесь мы не можем иметь, скажем, линию, похожую на известный “колокол” нормального распределения. Причина ясна: наша выборка конечна. Даже если в генеральной совокупности распределение, к примеру, нормально, а выборка - репрезентативна, мы вместо “колокола” получим лишь некоторое его подобие, составленное, например, из отрезков, соединяющих отдельные точки - полигон распределения (рис. 3).

Рис 3. Полигон плотности распределения непрерывного признака

От середин отрезков, отложенных на горизонтальной оси, откладываются, соответственно, 20%, 25%, 35%, 10%, 10%

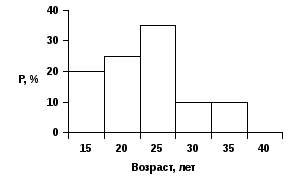
Рис. 4. Гистограмма плотности распределения непрерывного признака

Разбив на интервалы, мы ставим другие вопросы. Рассмотрим наиболее часто встающие.

К какому интервалу относить объект, для которого значение рассматриваемого признака лежит на “стыке” двух интервалов?Ответом на него обычно служит соглашение: скажем, все “стыки” считать принадлежащими правому интервалу (используя известные математические обозначения, можно сказать, например, что при разбиении диапазона изменения возраста на равные интервалы по 5 лет, мы в действительности будем рассматривать полуинтервалы: [15, 20), [20, 25) и т.д. Последним полуинтервалом может быть, например, [60, 65). Заметим, что фактически используемая нами при этом модель (мы уже неоднократно подчеркивали, что какая-то модель всегда стоит за любым, даже самым простым, математическим методом, и что для социолога раскрытие смысла подобных моделей является первоочередной задачей) изучаемого явления может привести к неоправданному (хотя вряд ли большому, особенно для многочисленной выборки) сдвигу массива данных вправо. Это скажется, например, при расчете мер средней тенденции (их определение см. ниже).

Как в только что описанной ситуации поступать с правым концом самого правого интервала? Прибегая к только что приведенному примеру, переформулируем вопрос: что делать с возрастом 25 лет? Ответы могут быть разными: например, вместо полуинтервала [60,65) использовать отрезок[60,65]; ввести дополнительный полуинтервал [65,70). При достаточно репрезентативной выборке принятие любого из них приведет примерно к одному и тому же результату (точнее, результаты не будут статистически значимо отличаться друг от друга).

При построении полигонов и гистограмм встают свои вопросы.

От какой точки интервала проводить вертикаль, на которой будет откладываться величина процента при построении полигона? На этот вопрос мы ответили в работе[Толстова, 1998](см. также Приложение 1). Там соответствующая ситуация рассмотрена очень подробно. Здесь же лишь отметим, что вертикаль может начинаться в любой точке интервала (хотя на практике из иллюстративных соображений чаще всего используют его середину).

Конечно, при выборе разных точек, в процессе дальнейшего анализа данных, вообще говоря, будут получаться разные результаты. Однако если считать, что мы работаем в рамках интервальной шкалы, то соответствующее различие будет именно таким, которое с точки зрения теории измерений для этой шкалы вполне допустимо.

Чем отличаются друг от друга модели, которые мы фактически используем, строя, с одной стороны, - полигон, а, с другой, - гистограмму распределения?

В обоих случаях мы в процессе построения закономерности (коей является частотное распределение) теряем информацию о том, каким образом распределены объекты внутри каждого интервала, и восполняем эту потерю путем введения модельных предположений об этом распределении. Обычно считают, что полигон отвечает кусочно-линейной плотности распределения. При использовании же гистограммы полагают, что объекты равномерно распределены внутри каждого интервала.

9. Выборочным представлением собственно функции распределения (а не плотности) случайной величины, “стоящей” за рассматриваемым признаком, служит т.н. кумулята распределения, или график накопленных частот. Она обычно представляется в виде полигона, каждая вершина которого отвечает относительной частоте того, что признак принимает значение, не превышающее того, над которым эта вершина находится. Нетрудно понять, что кумулята получается из описанного выше полигона распределения путем последовательного суммирования определяющих его частот.

10. Как строить гистограмму с неравными интервалами?

Способ построения такой гистограммы опирается на только что сформулированное положение о площадях составляющих гистограмму прямоугольников. На примере опишем соответствующий алгоритм.

Предположим, что частотная таблица, на базе которой мы хотим построить гистограмму, отвечающую распределению нашей совокупности респондентов по возрасту, имеет вид, отраженный в таблице 2. .

Таблица 2