
Laba-11
.pdf
ЛАБОРАТОРНА РОБОТА №11
Дослідження нелінійних систем автоматичного регулювання методом фазової площини
Мета роботи: дослідити лінійну систему третього порядку та релейну систему автоматичного регулювання другого порядку методом фазової площини, а також дослідити вільний рух системи, періодичні режими, способи стабілізації системи при різних характеристиках нелінійного елемента.
Основні теоретичні положення
Релейні системи автоматичного регулювання знайшли широке застосування. До релейних систем відносяться системи з релейними підсилювальними та виконавчими пристроями. Багато автопілотів, авторульових для суден, систем регулювання температури та різні слідкуючі системи є нелінійними. Поряд із конструктивною простотою релейні системи володіють малим часом перехідного процесу.
Система із одним релейним елементом завжди може бути представлена у вигляді одноконтурної схеми, яка містить релейний елемент та лінійну частину
(рисунок 11.1).
Рисунок 11.1 – Структурна схема релейної системи
Хоча в загальному випадку неможливе точне інтегрування нелінійного диференціального рівняння, виявляється, в випадку релейних систем можна одержати точний розв’язок. В релейних системах нелінійна характеристика складається із кількох лінійних ділянок. Поки вхідний сигнал реле знаходиться в

межах однієї із цих ділянок, рух системи описується лінійним диференційним рівнянням.
В межах другої лінійної ділянки рівняння руху змінюється. Рухи на окремих ділянках повинні “припасовуватися” один до другого (за початковими та кінцевими умовами ділянок). Це припасовування особливо легко здійснюється, коли лінійна частина системи описується диференційним рівнянням другого порядку, якщо користуватися поняттям фазової площини.
Нелінійне диференціальне рівняння системи можна одержати наступним чином. Згідно із схемою (рисунок 11.1) рівняння помилки в зображенні Лапласа:
X (s) = f (s) − z(s) , |
(11.1) |
де
z(s) =Wл (s) y(s) , y(s) = L{Ф(x)}, |
(11.2) |
тоді
X (s) = f (s) −Wл (s) L{Ф(x)}. |
(11.3) |
Для того, щоб перейти до диференціальних рівнянь, необхідно знати функцію передачі лінійної частини.
Так у випадку при Wл (s) = 1 |
s |
одержимо наступне рівняння: |
|
|||
|
|
|
|
|
|
|
|
d 2 x |
+Ф(x) = |
d 2 f |
. |
(11.4) |
|
|
dt 2 |
|
||||
|
|
|
dt 2 |
|
||
В даній роботі розглядається автономна нелінійна система другого порядку із нелінійним диференціальним рівнянням виду:
d 2 x |
+Ф(x) =0 . |
(11.5) |
|
dt 2 |
|||
|
|
Якщо задатися початковими умовами для величини х та швидкості її зміни V = dxdt в момент часу t =0 :
x |
|
t =0 = x0 , |
V |
|
|
= |
dx |
|
|
=V0 , |
(11.6) |
|
|
||||||||||
|
|
t =0 |
dt |
|
|||||||
|
|
|
|
|
|
|
|
t =0 |
|
||
|
|
|
|
|
|
|
|
||||

то одержимо однозначно визначений розв’язок рівняння (11.5), тобто криву x(t) .
У випадку системи другого порядку дві величини X та V = dxdt повністю визначають стан системи в даний момент часу.
Площина, яка має декартовими координатами дві змінні, які повністю визначають стан системи, називається фазовою площиною. Стан системи другого порядку характеризується точкою на фазовій площині. Ця точка називається зображуючою точкою (наприклад, точка P на рисунку 11.2).
Рисунок 11.2 – Фазова площина
При русі системи відбувається зміна її стану, тобто змінюються фазові координати X та V . Тому зображуюча точка системи буде описувати деяку траєкторію, яка називається фазовою траєкторією. Дві фазові траєкторії не перетинаються одна з одною (крім особливих точок). Тому із кожної точки фазової площини виходить тільки одна траєкторія.
При вибраному напрямі осей координат (рисунок 11.2) рух зображуючої точки завжди здійснюється за годинниковою стрілкою.
На осі абсцис V =0 , X досягає максимальних значень. Фазова траєкторія перетинає вісь X під прямим кутом. Ці властивості фазових траєкторій дозволяють одержати чітку картину про залежність характеру руху від початкових умов. Сукупність фазових траєкторій, знайдених для всіх можливих

початкових умов, разом з т.зв. особливими точками та траєкторіями складає
фазовий портрет системи.
Щоб перейти до зображення процесів на фазовій площині, замінимо попередньо рівняння (11.5) двома рівняннями першого порядку:
dx |
=V |
|
|
|
|
|
|
||
dt |
|
|
||
|
. |
(11.7) |
||
dV |
|
|||
|
|
|
||
dt |
= −Ф(x) |
|
||
|
|
|
||
В більш загальному випадку нелінійного рівняння другого порядку рівняння (11.7) приймають вигляд:
dx |
= R(x, V ) |
|||
|
|
|
||
. |
||||
dt |
||||
|
dV |
= F(x, V ) |
||
|
|
|||
dt |
|
|||
В нашому конкретному випадку: |
|
|||
R(x, V )=V ; F(x, V )=ϕ(x).
Виключивши час t із рівняння (11.8), одержимо:
dVdx = FR((xx,, VV )).
(11.8)
(11.9)
(11.10)
Рівняння (11.10) представляє собою рівняння фазової траєкторії. Як неважко побачити – рівняння визначає напрям фазової траєкторії в неособливій точці.
В особливих точках, коли F(x, V )= 0 , R(x, V )= 0 , dV dx = 0 0 , не існує певного напряму дотичної до траєкторії в даній точці. Неважко побачити, що особливим точкам відповідає стан рівноваги.
Існує шість типів особливих точок: центр, стійкий фокус, нестійкий фокус, стійкий вузол, нестійкий вузол та особлива точка типу “сідло”.
В нелінійній системі на відміну від лінійної системи тип особливої точки не завжди визначає поведінку зображуючої точки на фазовій площині. Фазові

траєкторії нелінійної системи можуть мати різний вид в різних областях фазової площини. Фазовий портрет нелінійної системи може містити:
1)особливі точки;
2)сепаратриси – особливі траєкторії, які розділяють області із траєкторіями різного типу;
3)граничні цикли – особливі траєкторії, які представляють собою ізольовані замкнуті фазові траєкторії.
Найбільше практичне значення має вивчення систем, які містять особливі точки та граничні цикли.
До числа таких систем відносяться прості релейні схеми другого порядку.
Рисунок 11.3 – Досліджувана релейна система
Вроботі досліджується система, представлена на рисунку 11.3.
Вякості релейного елемента розглядаються ідеальне реле та реле із гістерезисом (рисунок 11.4).
а) ідеальне реле; б) реле з гістерезисом.
Рисунок 11.4 – Характеристики нелінійних елементів
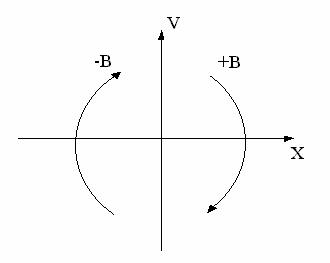
Кутовим точкам характеристики реле відповідають на фазовій площині (x, V ) т.зв. лінії переключення. Лінії переключення ділять фазову площину на ряд областей, кожній із яких відповідає своє диференціальне рівняння.
При перетині лінії переключення деякі із коефіцієнтів рівняння стрибкоподібно змінюють свої значення. Так у випадку системи з ідеальним реле лінією переключення служить лінія x = 0 , тобто вісь V .
Фазові траєкторії в цьому випадку на основі рівнянь (11.10):
dV |
= − |
|
B |
при x > 0; |
||||
dx |
|
|
||||||
|
V |
|
|
(11.11) |
||||
dV |
|
B |
|
|
|
|||
= |
|
при |
x < 0. |
|||||
dx |
|
|||||||
V |
|
|
|
|||||
Звідси випливає, що фазові траєкторії представляють собою параболи виду |
||||||||
(рисунок 11.5): |
|
|
|
|
|
|
|
|
V 2 |
+ Bx =C при |
x >0; |
||||||
2 |
||||||||
|
|
|
|
|
|
(11.12) |
||
V 2 |
|
|
|
|
|
|
||
− Bx =C |
при |
x <0. |
||||||
2 |
||||||||
|
|
|
|
|
|
|
||
В цьому випадку фазові траєкторії системи представляють собою замкнуті криві, та присутня особлива точка типу “центр”. В результаті в системі буде мати місце незатухаючий періодичний процес.
Рисунок 11.5 – Фазові траєкторії релейної системи

У випадку реле із гістерезисом аналогічні міркування показують, що в системі положення рівноваги не досягається. Це є наслідком того, що гістерезис вносить запізнювання при переключеннях порівняно із ідеальним реле.
Природно, що процеси в системі як у випадку ідеального реле, так і у випадку реле із гістерезисом, не можуть бути признані задовільними. Тому виникає задача стабілізації релейних систем. Стабілізацію релейних систем можна проводити двома способами:
1)введення сигналу похідної регульованої величини – корекція за швидкістю.
2)введення демпфування – жорсткого зворотного зв’язку.
Розглянемо корекцію по швидкості релейної системи другого порядку, яка представлена на рисунку 11.4.
В цьому випадку структурна схема системи приймає вигляд, представлений на рисунку 11.6. У випадку ідеального реле переключення будуть здійснюватись при переході через нуль.
Рівняння прямої переключення на фазовій площині приймає вигляд:
x + aV = 0, V = −x |
a |
. |
(11.13) |
|
|
|
В цьому випадку замість незатухаючого періодичного процесу одержимо затухаючий процес.
Рисунок 11.6 – Релейна система з корекцією за швидкістю

У випадку реле з гістерезисом процес вже не буде розбіжним, як раніше без корекції, а виникне стійкий граничний цикл. Збільшення a завжди приводить до зниження амплітуди та зростання частоти автоколивань.
Розглянемо тепер другий спосіб – введення демпфування. В цьому випадку одна інтегруюча ланка охоплюють жорстким зворотнім зв’язком (рисунок 11.7).
Рисунок 11.7 – Релейна схема із жорстким зворотним зв’язком
Нелінійне диференційне рівняння прийме вигляд:
d 2 x |
+ |
dx |
+Ф(x)= 0 . |
(11.14) |
|
dt 2 |
dt |
||||
|
|
|
Поява в диференційному рівнянні члена, пропорційного першій похідній dx dt =V , свідчить про наявність затухання в системі.
Рівняння фазових траєкторій приймає вигляд:
x +V −B ln(V + B) = C при |
x > 0; |
(11.15) |
|
x +V + B ln(V −B) = C при |
x < 0. |
||
|
У випадку введення демпфування в систему із ідеальним реле лінією переключення буде лінія x = 0 , тобто вісь V , але зміниться вид фазових траєкторій. При цьому процеси будуть затухати – система стає стійкою. З'являється одна особлива точка – стійкий фокус.
У випадку реле із гістерезисом має місце один стійкий граничний цикл. Відповідний вибір коректуючого кола дозволяє різко понизити амплітуду автоколивань та збільшити частоту.

Порядок виконання роботи
1)Вивчити теоретичні відомості.
2)В системі MATLAB запустити програму Simulink.
3)Визначити критичний коефіцієнт підсилення лінійної системи третього порядку.
4)Побудувати перехідні характеристики системи та відповідні фазові траєкторії лінійної системи в стійкому, нестійкому станах та на межі стійкості системи. В останньому випадку також визначити параметри автоколивань (за фазовою траєкторією).
5)Зняти статичні характеристики ідеального двохпозиційного реле та реле з гістерезисом.
6)На вхід системи подати короткочасний імпульс невеликої амплітуди.
7)Скласти структурну схему релейної системи (рисунок 11.8). Реле ідеальне, d=0,
γ=0.
8) Задати початкові умови на інтеграторах. З виходу першого інтегратора напругу подати на вхід “Y” осцилографа, а з виходу другого інтегратора – на вхід “X”.
Рисунок 11.8 – Структурна схема досліджуваної системи
9)Зарисувати осцилограми фазових траєкторій при нульових початкових умовах: x(0)= 0 В, V (0)= 0 В. Визначити амплітуду та частоту періодичних коливань.
10)Ввести сигнал похідної помилки. Для цього встановити довільне значення коефіцієнта d (в межах 0.001-0.1). Зарисувати фазову траєкторію при x(0)= 0 та
V (0)= 0 .
11)Замінити ідеальне реле на реле із гістерезисом. Відключити зворотні зв’язки. Встановити x(0)= 0 В, V (0)= 0 В. Зарисувати фазову траєкторію.
12)Зарисувати фазову траєкторію системи з гістерезисом при введенні сигналу похідної помилки. Встановити початкові умови: x(0)= 0 В, V (0)= 0 В. Значення d
взяти з п. 10. Визначити параметри автоколивань. Зарисувати перехідний процес в системі.
13)Розімкнути зворотній зв’язок по колу d та ввести жорсткий зворотній зв’язок по колу γ (рисунок 11.8). Встановити значення коефіцієнта γ в діапазоні 0.001-0.1. Зарисувати фазову траєкторію при x(0)= 0 B та V (0)= 0 В (у випадку з ідеальним двохпозиційним реле).
14)Замінити ідеальне реле на реле із гістерезисом. Значення γ залишити незмінним. Зарисувати фазові траєкторії. Побудувати перехідну характеристику в системі.
15)Зробити висновки про типи особливих точок та граничні цикли на фазових траєкторіях.
16)Оформити звіт. Відповісти на контрольні питання.
Зміст звіту
1)Титульний лист: назва дисципліни, номер і назва роботи, прізвище, ім’я, по батькові студента, дата виконання.
2)Мета роботи, завдання згідно варіанту.
3)Структурна схема лінійної САУ.
4)Фазові траєкторії лінійної системи в трьох станах.
5)Структурні схеми релейних САУ.
6)Фазові траєкторії та перехідні процеси в релейних системах (з різними видами корекції).
7)Висновки.
