
- •Телков А.П., Грачёв С.И. Гидромеханика пласта применительно к прикладным задачам разработки нефтяных и газовых месторождений: учебное пособие. В 2 ч. Ч.1. – Тюмень: ТюмГНГУ, 2009. – 240 с.
- •ПРЕДИСЛОВИЕ
- •Рис. 1.1. Схема укладки фиктивного грунта
- •Рис. 5.2. Схема безнапорного притока к совершенной скважине-колодцу
- •Рис. 6.2. Схема прямолинейного движения границы раздела двух жидкостей
- •Рис. 6. 14. Распределение насыщенности при вытеснении нефти водой
- •при линейном вытеснении нефти водой:
Глава 5. БЕЗНАПОРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
ВПОРИСТОЙ СРЕДЕ
5.1.Особенности безнапорного движения
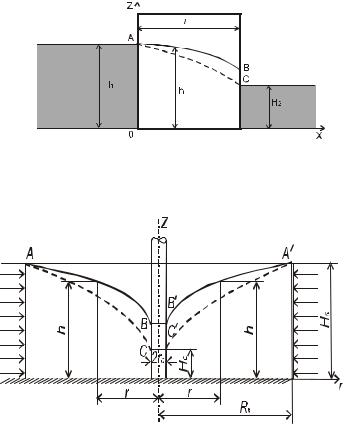
Впредыдущих разделах мы рассматривали движение жидкости в порах по всей толщине пласта. При этом пьезометрическая поверхность располагалась выше кровли пласта. Здесь мы рассмотрим движение жидкости, свободная поверхность которой находится ниже кровли пласта и является в то же время пьезометрической поверхностью. Такое движение называется безнапорным. Примерами безнапорного движения могут служить фильтрация грунтовых вод через земляную плотину и приток их к скважине
—колодцу (рис. 5.1 и 5.2).
Рис. 5.1. Схема безнапорного течения через проницаемую |
перемычку при горизонтальном непроницаемом основании |
Рис. 5.2. Схема безнапорного притока к совершенной скважине-колодцу |
76 |
Безнапорное движение жидкости встречается также при шахтной добыче нефти, в условиях гравитационного режима и вследствие истощения пластовой энергии, когда уровень жидкости (свободная поверхность) оказывается ниже кровли пласта.
Для инженерных расчетов пользуются гидравлической теорией безнапорного движения, которая является неправильной. Однако расчетные данные для дебитов хорошо совпадают с экспериментальными результатами. В описании же свободной поверхности в приближенной гидравлической теории имеется большая погрешность, так как не учитывается промежуток высачивания ВС (см. рис. 5.1).
Введем некоторые понятия. Уровень Н1 называется верхним бьефом, уровень Н2 — нижним бьефом; ВС — промежуток высачивания, через который жидкость сочится в атмосферу и стекает в нижний бьеф. Поверхность ABC представляет собой пьезометрическую (депрессионную) поверхность. Свободная поверхность АВ всегда выходит выше нижнего бьефа. Те же самые понятия остаются и для безнапорного притока к колодцу.
Основная трудность точного решения задач безнапорного движения состоит в том, что неизвестна форма области движения жидкости, тогда как при напорной фильтрации она известна, поскольку кровля и подошва фиксированы.
Некоторые точные решения для безнапорного движения через прямоугольную перемычку выполнены П. Я. Полубариновой-Кочиной. Для притока к колодцу до сих пор точного решения не имеется.
Рис. 5.3. Схема к выводу дифференциального уравнения стационарной безнапорной фильтрации через прямоугольную перемычку
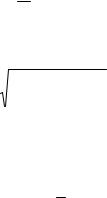
Рассмотрим приближенную гидравлическую теорию. Проведем произвольное вертикальное сечение в безнапорном потоке (рис. 5.3), где h есть ордината точки свободной поверхности в данном сечении, i — sin α — уклон свободной поверхности. Делаются следующие допущения: 1) горизонтальные компоненты скорости распределены равномерно;
77

2) давление вдоль вертикали распределено по гидростатическому закону, т. е. «напор» Н = Z + γр = Н (х, z). «Напор», таким образом, вдоль каждой
вертикали предполагается постоянным. Эти предпосылки допустимы в тех областях течения, где i2 << l и кривизна линии тока меньше i, т. е. вдали от промежутка высачивания (i ≈ 1). Будем считать, что над свободной поверхностью Р = Рат, т. е. избыточное давление равно нулю. Принимая за избыточное давление р = 0, находим, что «напор» Н равен глубине потока h, т. е. Н = h, откуда по закону Дарси следует выражение для поверхностной скорости фильтрации
υn = −C |
dH |
|
= −C |
dh |
. |
(5.1) |
|
dS |
|
||||||
|
|
|
|
dS |
|
||
Горизонтальная компонента скорости фильтрации |
|
||||||
u = −C |
dh |
. |
(5.2) |
||||
|
|||||||
|
|
|
dх |
|
|||
Эта компонента предполагается постоянной вдоль вертикали. Вертикальная компонента по условию равна нулю.
Расход на единицу ширины потока f = 1 запишется выражением
q = uhf = −Сh |
dh |
. |
(5.3) |
|
|||
|
dx |
|
|
Итак, мы видим, что отличительным признаком безнапорного движения является линейная зависимость потенциала или функции Н на свободной поверхности от вертикальной координаты Z.
5.2. Гидравлическая теория безнапорного движения через прямоугольную перемычку на горизонтальном основании
Определим из (5.3) уравнение свободной поверхности. Разделяя переменные и интегрируя, получим
qx = − |
Сh2 |
+ const. |
(5.4) |
|
2 |
||||
|
|
|
Используя граничные условия (см. рис. 5.1)
x = 0 при |
h = H1 |
, |
(5.5) |
|
x = l при |
h = H 2 , |
|||
|
||||
находим
78
|
|
CH 2 |
|
||
const = |
|
1 |
; |
||
|
2 |
||||
|
|
|
|
||
|
CH 2 |
|
|
|
|
ql = − |
|
2 |
|
+const. |
|
2 |
|
|
|||
|
|
|
|
|
|
Решая совместно (5.6) и (5.7), находим расход: q = 2Cl (H12 − H 22 ).
Подставляя (5.6) в (5.4) и учитывая (5.8), находим
h = H12 − |
H 2 |
− H 2 |
|
1 |
2 |
x. |
|
|
l |
||
|
|
|
(5.6)
(5.7)
(5.8)
(5.9)
Получили уравнение параболы. Таким образом, поверхность депрессии является параболой (линия АС, рис 5.1). В действительности формула (5.9) несправедлива. Это видно из следующих соображений. При Р2 = 0 у выхода в нижний бьеф (х = l) из формулы (5.9) получаем, что h = 0. Это приводит к
бесконечной скорости фильтрации u = qh = ∞, что невозможно. Поэтому
необходимо, чтобы выполнялось условие hx=l > H2, т. е. должен существовать промежуток высачивания.
Формула Дюпюи (5.8), хотя и выведена из допущений гидравлической теории, является строго точной. Строгое доказательство ее дано И.А. Чарным
[5].
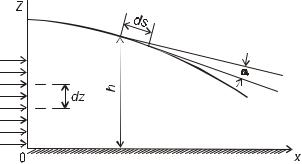
5.3.Гидравлическая теория безнапорного притока
ксовершенной скважине
Рассмотрим приток к совершенной скважине. Все обозначения даны на рис. 5.2. Движение считаем установившимся, т. е. Q и h = h (r) от времени не зависят. Скважину считаем стоком, следовательно, дебит будет положительным.
Скорость фильтрации по закону Дарси
υr = C |
dh |
. |
(5.10) |
|
|||
|
dr |
|
|
Если f = 2πrh — площадь фильтрации при |
плоскорадиальном |
||
притоке, то дебит скважины выразится формулой |
|
||
79

Q = f |
|
υr |
|
= 2πrhC |
dh . |
(5.11) |
|
|
|||||
|
|
|
|
|
dr |
|
|
|
|
|
|
|
Знак минус здесь не ставим, так как мы рассматриваем скважину-сток, а функция h = h (r) является возрастающей функцией расстояния.
Разделяя переменные в уравнении (5.11) и интегрируя, получаем
Q ln r = π С h2 +const. |
(5.12) |
Из граничного условия h = Hк при r = Rк находим |
|
const =Qln Rк − πСНк2 . |
(5.13) |
Подставляя (5.13) в (5.12), найдем уравнение свободной поверхности (АСС’A’, рис. 5.2). Используя второе граничное условие h = Hc при r = rc и выражение (5.13), из (5.12) получаем формулу Дюпюи
Q = |
πC (H |
к2 − H с2 ). |
(5.14) |
|
|
||||
|
ln |
Rк |
|
|
r |
|
|||
|
|
|
||
|
|
c |
|
|
Формула (5.14), как и формула (5.8), является строго точной.
5.4. Дифференциальные уравнения гидравлической теории нестационарной безнапорной фильтрации
Согласно гидравлической теории безнапорного движения считается, что напор Н = Н (х, у, z, t) является постоянной величиной вдоль каждой вертикали, а горизонтальные проекции скорости фильтрации u, υ равномерно распределены вдоль каждой вертикали. Тогда напор равен глубине потока (Н = h) и компоненты скорости запишутся в следующем виде:
u = −C |
∂H |
; |
|
|
∂x |
(5.15) |
|
|
∂H |
||
υ = − C |
. |
||
∂y |
|||
|
|
Расходы потока на единицу ширины в направлениях х и у соответственно будут равны:
qx = uf = uH 1 |
= −C |
∂H |
H = −C |
|
∂ 1 |
H |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||
∂x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∂x 2 |
|
|
|
|
|
(5.16) |
||||||||
|
|
|
∂H |
|
|
∂ 1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
||||||||||
q y = υf = υH 1 |
= −C |
∂y |
H = −C |
|
|
|
|
|
H |
|
. |
|
||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
∂y 2 |
|
|
|
|
|
||||||||
80
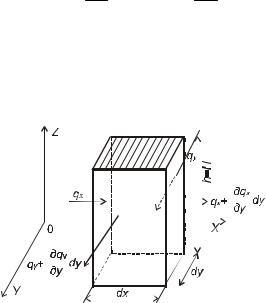
Составим уравнение неразрывности для нестационарного грунтового потока. Выделим элемент грунта высотой Н = h и площадью сечения dxdy (рис. 5.4). За время dt в параллелепипед поступает
V1 = (qx dy + qy dx)dt .
Вытекает за то же время
V2 = qx + ∂∂qxx dx dy + q y + ∂∂qyy dy dx dt .
Следовательно, накопленный объем за время dt составит
|
|
|
|
|
|
∂q |
x |
|
|
∂q y |
|
|
|
|
|
|||||||
dV =V |
−V |
2 |
= − |
|
|
+ |
|
|
|
|
|
|
dxdy dt . |
(5.17) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.4. Схема к выводу уравнения гидравлической теории
Этот объем идет на повышение высоты Н, которая за время dt меняется
на величину |
∂H |
dt . Учитывая |
пористость |
т, изменение |
объема можно |
|||||||||
∂t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
записать еще в таком виде |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dV = m |
|
∂H |
|
dtdxdy . |
(5.18) |
||||||
|
|
|
|
|
∂t |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приравнивая (5.17) и (5.18), находим |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∂H |
|
|
∂q |
x |
|
∂q y |
|
||||
|
|
m |
|
= − |
|
|
+ |
|
|
. |
(5.19) |
|||
|
|
|
|
|
|
|
||||||||
|
|
|
∂t |
|
|
∂x |
|
|
|
|
|
|||
|
|
|
|
|
|
∂y |
|
|||||||
81
Подставляя значение qx и qy из (5.16) в (5.19), получим |
|
|
|
|||||||||||||||||||||
|
∂H |
|
|
∂2 |
|
1 |
|
|
2 |
|
|
∂2 |
|
1 |
|
2 |
|
(5.20) |
||||||
m |
∂t |
= C |
|
|
|
|
|
|
|
H |
|
+ |
|
|
|
|
|
H |
|
|
||||
∂x |
2 |
2 |
|
∂y |
2 |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂H |
|
|
C |
|
|
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
(5.21) |
|||
|
|
|
|
|
= |
|
|
|
|
|
|
|
H |
|
. |
|
|
|
|
|||||
|
|
∂t |
|
m |
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Получили дифференциальное уравнение гидравлической теории нестационарного безнапорного потока Буссинеска. Как видим, уравнение это нелинейное, параболического типа, в частных производных. В общем случае точного решения не имеет. Точные решения для частных случаев имеются у П.Я. Полубариновой-Кочиной.
Одним из методов приближенного решения подобных уравнений является метод линеаризации Л.С. Лейбензона. Л.С. Лейбензон указал замечательное сходство уравнения (5.21) с дифференциальным уравнением неустановившегося движения газа в пористой среде. В дальнейшем мы рассмотрим эту аналогию.
82
Глава 6. ЗАДАЧИ ВЫТЕСНЕНИЯ ОДНОЙ ЖИДКОСТИ ДРУГОЙ. ФИЛЬТРАЦИЯ НЕОДНОРОДНЫХ ЖИДКОСТЕЙ
6.1. Общие представления о продвижении краевых
иподошвенных вод к нефтяным и газовым скважинам
Впроцессе эксплуатации нефтяных и газовых залежей при водонапорном режиме пласта в простейших случаях различают продвижение поверхности раздела двух фаз как наступление краевой воды и как подъем подошвенной воды к забоям скважин. Первый случай относится преимущественно к продуктивным пластам незначительной толщины с большим углом падения структуры, где вода продвигается вдоль напластования: второй случай — к пластам с малым углом наклона, особенно при большой продуктивной толщине.
Взалежах с водонапорным режимом при наступлении краевых вод продуктивная площадь со временем уменьшается. Равномерность стягивания контура нефтеносности при этом зависит от коллекторских свойств пласта и характера эксплуатации краевых скважин; здесь могут быть «языки обводнения». Приближенная теория продвижения краевых вод и регулирования контура нефтеносности нашла отражение в многочисленных работах советских и зарубежных гидродинамиков: Л. С. Лейбензона, В. Н. Щелкачева, П. Я. Полубариновой-Кочиной, И. А. Чарного, М. Маскета и др.
Физическая сторона гидродинамического исследования задач о продвижении подошвенной и краевой воды различна. Можно выделить три вида притока нефти (газа) к скважинам с подошвенной водой: 1) вытеснение нефти происходит вдоль напластования за счет продвижения контурной воды, подошвенная вода не принимает участия в вытеснении или она малоактивна; 2) нефть поступает к скважинам в основном под напором подошвенной воды, краевые воды малоактивны; 3) приток нефти к скважинам осуществляется за счет одновременного продвижения контурных
иподошвенных вод.
Впервом случае подошвенная вода не участвует в вытеснении нефти, однако вследствие отбора нефти проявляется тенденция к деформированию поверхности раздела двух фаз, которая принимает холмообразный вид, называемый конусом подошвенной воды. При установившихся условиях отбора поверхность раздела (конус подошвенной воды) находится в равновесии и не оказывает существенного влияния на приток нефти к скважине. Если превысить депрессию и отбор нефти или газа сверх некоторой предельной величины, то вода прорвется в скважину, что может привести к прогрессирующему обводнению ее. Таким образом, в этом случае существует предельная высота вершины конуса, при которой конус находится в статическом равновесии. Этой высоте соответствуют предельные депрессия и величина безводного дебита нефти, которые приближенно можно рассчитать. Методы расчета будут приведены в следующих разделах.
83
Во втором случае линии тока имеют почти перпендикулярное направление к первоначально горизонтальной поверхности раздела, и только вблизи забоя несовершенной скважины это направление меняется. Полагают, что вытеснение нефти происходит вследствие поднятия поверхности подошвенной воды. Наибольшая скорость поднятия поверхности раздела отметится на оси скважины и с приближением к забою скорость будет увеличиваться. Качественно здесь форма конуса такая же, как и в первом случае, но вопрос о статическом равновесии поверхности раздела исключается ввиду напора подошвенных вод. Остается решать задачу прорыва подошвенной воды к забою несовершенной скважины, что весьма интересно для нефтепромысловой практики. Аналитические решения этой задачи известны в приближенной постановке при некоторых допущениях.
Третий случай наиболее сложный, и аналитическое решение применить к нему весьма затруднительно. Однако приближенно решение можно свести здесь к одному из первых двух случаев.
6.2. Вытеснение нефти водой из трубки тока переменного сечения
Строгое гидродинамическое решение задачи о движении границы раздела двух жидкостей в общем случае отсутствует. Оно существует для прямолинейного и плоскорадиального притоков. Эти задачи возникли в связи с вопросом о стягивании контура нефтеносности или газоносности при водонапорном режиме течения в процессе разработки нефтяной или газовой залежи.
Впервые указанная задача была поставлена и решена Л. С. Лейбензоном. При этом полагалось, что давление на границе раздела остается постоянным, т. е. вязкость воды μв = 0.
Маскет рассмотрел задачу в постановке, когда вязкость воды отлична от нуля, μв ≠ 0, и первоначальная граница раздела совпадает с контуром питания. Более общий случай, когда первоначальная граница и контур питания не совпадают, был исследован В. Н. Щелкачевым.
Рассмотрим задачу о продвижении границы раздела в постановке И. А. Чарного. Пусть трубка тока переменного сечения ω(s) заполнена пористой средой, насыщенной водой и нефтью (рис. 6.1). Полагаем, что вытеснение происходит «поршневым» образом, т. е. считаем границу раздела некоторой поверхностью (на самом деле резкой границы раздела нет из-за происходящих в пористой среде капиллярных явлений).
Пренебрегая силами тяжести, для установившегося движения однородной несжимаемой жидкости по закону Дарси расход записываем формулой
Q = − |
k |
dp |
ω (s). |
(6.1) |
|
||||
|
μ ds |
|
|
|
84
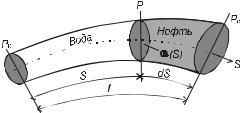
Рис.6.1. Схема вытеснения нефти водой из трубки тока переменного сечения
Разделяя переменные в (6.1) и интегрируя в соответствующих пределах, получаем
|
р1 − |
(6.2) |
|||
Q = − |
р2 |
. |
|||
s2 |
|
||||
|
|
|
|
||
|
μ∫ |
ds |
|
|
|
|
kω (s) |
||||
|
s1 |
|
|
|
|
Здесь объемный расход Q во всех сечениях трубки тока одинаковый, т. к. жидкость считается несжимаемой и движение — установившееся. Вводя фильтрационное сопротивление
s |
|
|
|
|
|
R = μ∫2 |
ds |
, |
|
(6.3) |
|
kω (s) |
|||||
s1 |
|
|
|
|
|
формулу (6.2) запишем в виде |
|
|
|
|
|
Q = − |
р1 − р2 |
. |
(6.4) |
||
|
|||||
|
|
R |
|
||
Всилу неразрывности потока выражение для расхода через сечение
ω(s) может быть представлено следующим образом:
Q = |
pк − p |
= |
p − pс |
. |
||||
S |
|
|||||||
|
|
S |
||||||
|
μв ∫0 |
ds |
|
|
μн ∫0 |
ds |
|
|
|
kω (s) |
|
kω (s) |
|||||
По правилу производных пропорций имеем
|
p |
− p |
с |
|
|
Q = |
|
к |
, |
(6.5) |
|
|
R (s) |
|
где
85
