
Нахождение площади фигуры
.docxНахождение площади фигуры, ограниченной линиями y=f(x), x=g(y).
В разделе геометрический смысл определенного интеграла мы разобрались с нахождением площади криволинейной трапеции G. Вот полученные формулы:
-
 для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b],
для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b], -
 для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].
для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].
Однако при решении задач на нахождение площади очень часто приходится иметь дело с более сложными фигурами.
В этой статье мы поговорим о вычислении площади фигур, границы которых заданы функциями в явном виде, то есть, как y=f(x) или x=g(y), и подробно разберем решение характерных примеров.
Навигация по странице.
-
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
-
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
Теорема.
Пусть
функции ![]() и
и ![]() определены
и непрерывны на отрезке [a;b],
причем
определены
и непрерывны на отрезке [a;b],
причем ![]() для
любого значения x из [a;b].
Тогда площадь
фигуры G,
ограниченной линиями x=a, x=b,
для
любого значения x из [a;b].
Тогда площадь
фигуры G,
ограниченной линиями x=a, x=b, ![]() и
и ![]() вычисляется
по формуле
вычисляется
по формуле  .
.
Аналогичная
формула справедлива для площади фигуры,
ограниченной линиями y=c,y=d, ![]() и
и ![]() :
:  .
.
Доказательство.
Покажем справедливость формулы для трех случаев:

В
первом случае, когда обе функции
неотрицательные, в силу свойства
аддитивности площади сумма
площади исходной фигуры G и
криволинейной трапеции ![]() равна
площади фигуры
равна
площади фигуры ![]() .
Следовательно,
.
Следовательно,

Поэтому,  .
Последний переход возможен в силу
третьего свойства
определенного интеграла.
.
Последний переход возможен в силу
третьего свойства
определенного интеграла.
Аналогично,
во втором случае справедливо равенство  .
Вот
графическая иллюстрация:
.
Вот
графическая иллюстрация:

В
третьем случае, когда обе функции
неположительные, имеем  .
Проиллюстрируем
это:
.
Проиллюстрируем
это:

Теперь
можно переходить к общему случаю, когда
функции ![]() и
и ![]() пересекают
ось Ox.
пересекают
ось Ox.
Обозначим
точки пересечения ![]() .
Эти точки разбивают отрезок [a;
b]на n частей
.
Эти точки разбивают отрезок [a;
b]на n частей ![]() ,
где
,
где ![]() .
Фигуру Gможно
представить объединением фигур
.
Фигуру Gможно
представить объединением фигур ![]() .
Очевидно, что на своем интервале
.
Очевидно, что на своем интервале ![]() попадает
под один из трех рассмотренных ранее
случаев, поэтому их площади находятся
как
попадает
под один из трех рассмотренных ранее
случаев, поэтому их площади находятся
как

Следовательно,

Последний переход справедлив в силу пятого свойства определенного интеграла.
Графическая
иллюстрация общего случая.

Таким
образом, формула  доказана.
доказана.
Пришло время перейти к решению примеров на нахождение площади фигур, ограниченных линиями y=f(x) и x=g(y).
К началу страницы
Примеры вычисления площади фигуры, ограниченной линиямиy=f(x) или x=g(y).
Решение каждой задачи будем начинать с построения фигуры на плоскости. Это нам позволит сложную фигуру представить как объединение более простых фигур. При затруднениях с построением обращайтесь к статьям: основные элементарные функции, их свойства и графики; геометрические преобразования графиков функций и исследование функции и построение графика.
Пример.
Вычислить
площадь фигуры, ограниченной параболой ![]() и
прямыми
и
прямыми ![]() , x=1, x=4.
, x=1, x=4.
Решение.
Построим эти линии на плоскости.

Всюду
на отрезке [1;4] график
параболы ![]() выше
прямой
выше
прямой ![]() .
Поэтому, применяем полученную ранее
формулу для площади и вычисляем
определенный интеграл по формуле
Ньютона-Лейбница:
.
Поэтому, применяем полученную ранее
формулу для площади и вычисляем
определенный интеграл по формуле
Ньютона-Лейбница:

Немного усложним пример.
Пример.
Вычислить
площадь фигуры, ограниченной линиями ![]() .
.
Решение.
В чем здесь отличие от предыдущих примеров? Ранее у нас всегда были две прямых, параллельных оси абсцисс, а сейчас только одна x=7. Сразу возникает вопрос: где взять второй предел интегрирования? Давайте для этого взглянем на чертеж.

Стало
понятно, что нижним пределом интегрирования
при нахождении площади фигуры является
абсцисса точки пересечения графика
прямой y=x и
полу параболы ![]() .
Эту абсциссу найдем из равенства:
.
Эту абсциссу найдем из равенства:
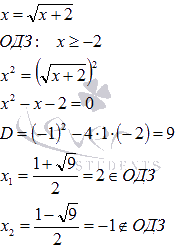
Следовательно, абсциссой точки пересечения является x=2.
Обратите внимание.
В
нашем примере и по чертежу видно, что
линии ![]() и y=x пересекаются
в точке(2;2) и
предыдущие вычисления кажутся излишними.
Но в других случаях все может быть не
так очевидно. Поэтому рекомендуем всегда
аналитически вычислять абсциссы и
ординаты точек пересечения линий.
и y=x пересекаются
в точке(2;2) и
предыдущие вычисления кажутся излишними.
Но в других случаях все может быть не
так очевидно. Поэтому рекомендуем всегда
аналитически вычислять абсциссы и
ординаты точек пересечения линий.
Очевидно,
график функции y=x расположен
выше графика функции ![]() на
интервале [2;7].
Применяем формулу для вычисления
площади:
на
интервале [2;7].
Применяем формулу для вычисления
площади:

Еще усложним задание.
Пример.
Вычислить
площадь фигуры, ограниченной графиками
функций ![]() и
и ![]() .
.
Решение.
Построим
график обратной пропорциональности ![]() и
параболы
и
параболы ![]() .
.

Прежде
чем применять формулу для нахождения
площади фигуры, нам нужно определиться
с пределами интегрирования. Для этого
найдем абсциссы точек пересечения
линий, приравняв выражения ![]() и
и ![]() .
.
При
отличных от нуля значениях x равенство ![]() эквивалентно
уравнению третьей степени
эквивалентно
уравнению третьей степени ![]() с
целыми коэффициентами. Можете обратиться
к разделу решение
кубических уравнений чтобы
вспомнить алгоритм его решения.
с
целыми коэффициентами. Можете обратиться
к разделу решение
кубических уравнений чтобы
вспомнить алгоритм его решения.
Легко
проверить, что x=1 является
корнем этого уравнения: ![]() .
.
Разделив
выражение ![]() на
двучлен x-1,
имеем:
на
двучлен x-1,
имеем:
![]()
Таким
образом, оставшиеся корни находятся из
уравнения ![]() :
:

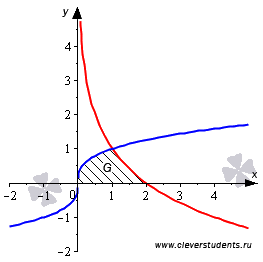
Теперь
из чертежа стало видно, что фигура G заключена
выше синей и ниже красной линии на
интервале  .
Таким образом, искомая площадь будет
равна
.
Таким образом, искомая площадь будет
равна

Рассмотрим еще один характерный пример.
Пример.
Вычислить
площадь фигуры, ограниченной кривыми ![]() и
осью абсцисс.
и
осью абсцисс.
Решение.
Сделаем чертеж.
![]() -
это обычная степенная функция с
показателем одна треть, график
функции
-
это обычная степенная функция с
показателем одна треть, график
функции ![]() можно
получить из графика
можно
получить из графика ![]() отобразив
его симметрично относительно оси абсцисс
и подняв на единицу вверх.
отобразив
его симметрично относительно оси абсцисс
и подняв на единицу вверх.
Найдем точки пересечения всех линий.
Ось абсцисс имеет уравнение y=0.
Графики
функций ![]() и y=0 пересекаются
в точке (0;0) так
как x=0 является
единственным действительным корнем
уравнения
и y=0 пересекаются
в точке (0;0) так
как x=0 является
единственным действительным корнем
уравнения ![]() .
.
Графики
функций ![]() и y=0 пересекаются
в точке (2;0),
так как x=2является
единственным корнем уравнения
и y=0 пересекаются
в точке (2;0),
так как x=2является
единственным корнем уравнения ![]() .
.
Графики
функций ![]() и
и ![]() пересекаются
в точке (1;1),
так как x=1является
единственным корнем уравнения
пересекаются
в точке (1;1),
так как x=1является
единственным корнем уравнения ![]() .
Это утверждение не совсем очевидно,
но
.
Это утверждение не совсем очевидно,
но ![]() -
функция строго возрастающая, а
-
функция строго возрастающая, а ![]() -
строго убывающая, поэтому, уравнение
-
строго убывающая, поэтому, уравнение ![]() имеет
не более одного корня.
имеет
не более одного корня.
Как же действовать дальше? Здесь есть несколько вариантов.
-
Можно фигуру G представить суммой двух криволинейных трапеций. Первая фигура расположена выше оси абсцисс и ниже синей линии на отрезке
 ,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке
,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке  .
Следовательно,
искомая площадь будет равна
.
Следовательно,
искомая площадь будет равна  .
. -
Можно фигуру G представить разностью двух фигур. Первая фигура является криволинейной трапецией и расположена выше оси Ox и ниже синей линии на отрезке
 ,
вторая фигура расположена выше красной
и ниже синей линии на отрезке
,
вторая фигура расположена выше красной
и ниже синей линии на отрезке  .
В
этом случае площадь представляем как
.
В
этом случае площадь представляем как  .
. -
А можно фигуру G рассматривать на отрезке
 ,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.
,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.
Единственное
замечание: в этом случае для нахождения
площади придется использовать формулу
вида  .
То есть, ограничивающие линии нужно
представить в виде функций от аргумента y.
Это сделать в нашем случае достаточно
легко. Разрешим уравнения
.
То есть, ограничивающие линии нужно
представить в виде функций от аргумента y.
Это сделать в нашем случае достаточно
легко. Разрешим уравнения ![]() и
и ![]() относительно x:
относительно x:

Таким
образом, искомая площадь равна

Мы бы пришли к этому же результату и в двух других случаях.
Можно переходить к последнему примеру.
Пример.
Вычислить
площадь плоской фигуры, ограниченной
линиями ![]() .
.
Решение.
С
построением этих линий проблем возникнуть
не должно. На чертеже красной линией
изображен график функции ![]() ,
синей линией
,
синей линией ![]() ,
а черной линией
,
а черной линией ![]() .
.

Определим точки пересечения линий.
Начнем
с графиков функций ![]() и
и ![]() :
:

Найдем
точку пересечения графиков функций ![]() и
и ![]() :
:

Осталось
найти точку пересечения прямых ![]() и
и ![]() :
:

Дальше можно поступить двояко:
-
Площадь искомой фигуры можно представить суммой площадей фигур, изображенных на рисунке
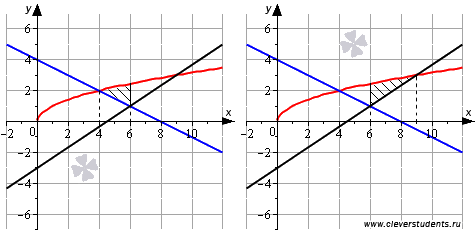
Тогда
площадь фигуры равна:

-
Также можно было площадь исходной фигуры выразить суммой площадей, показанных на чертеже

Для
этого случая, перед применением формулы
для вычисления площади фигуры, разрешим
уравнения линий относительно x:

Таким
образом, площадь равна:

Как видите, значения совпадают.
К началу страницы
Подведем итог.
Мы разобрали все наиболее часто встречающиеся случаи нахождения площади фигуры, ограниченной явно заданными линиями. Для этого нужно уметь строить линии на плоскости, находить точки пересечения линий и применять формулу для нахождения площади, что подразумевает наличие навыков вычисления определенных интегралов.
