
- •1. ИНФОРМАЦИЯ О ДИСЦИПЛИНЕ
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. РАБОЧИЕ УЧЕБНЫЕ МАТЕРИАЛЫ
- •2.1. Рабочая программа
- •2.3. Структурно-логическая схема дисциплины
- •2.4. Временной график изучения дисциплины
- •2.5. Практический блок
- •2.6. Рейтинговая система оценки знаний при использовании ДОТ
- •3. ИНФОРМАЦИОННЫЕ РЕСУРСЫ ДИСЦИПЛИНЫ
- •3.1. Библиотический список
- •3.2. ОПОРНЫЙ КОНСПЕКТ
- •ВВЕДЕНИЕ
- •Раздел 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- •Раздел 2. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ПЕРЕМЕННЫЙ ТОК
- •Раздел 3. ВОЛНОВЫЕ ПРОЦЕССЫ
- •Раздел 4. ВОЛНОВАЯ ОПТИКА
- •ЗАКЛЮЧЕНИЕ
- •ГЛОССАРИЙ
- •4. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ
- •ТЕСТЫ К РАЗДЕЛУ 2
- •ТЕСТЫ К РАЗДЕЛУ III
- •ТЕСТЫ К РАЗДЕЛУ 4
- •СОДЕРЖАНИЕ

Раздел 3. ВОЛНОВЫЕ ПРОЦЕССЫ
В разделе 3 изучаются три темы: 3.1. Характеристики волнового процес-
са; 3.2. Энергия упругой волны; 3.3. Электромагнитные волны.
В конце каждой темы вы должны ответить на поставленные вопросы, а по завершению изучения раздела выполняется тестовое задание.
Максимально возможное число баллов, которое можно получить при работе с материалом данного раздела, равно 20.
Подробное изложение материала раздела представлено в учебном пособии А.Б. Федорцова, В.М. Цаплева «Курс физики. Колебания и волны. Волно-
вая оптика», а также: [1], c. 318…327, 333…340; [2], c. 284…290, 297…303.
По материалам раздела выполняются задачи 415…420, 436...438 из контрольной работы № 4.
3.1.Характеристики волнового процесса
3.1.1.Образование волн. Принцип Гюйгенса
Рис. 3.1
то это колебание не остается локализованным на одном маятнике – наличие связи между маятниками приводит к передаче колебательного движения (а, следовательно, и энергии) от одного маятника к другому.
Сплошную упругую среду можно представить как систему материальных точек, связанных между собой упругими связями. Если в каком-либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия ме-
52
ду частицами это колебание будет распространяться в среде от частицы к час-
тице с некоторой скоростью υ. При этом и энергия будет передаваться от частицы к частице. Так образуется упругая волна.
Процесс распространения колебаний в пространстве, сопровождающийся переносом энергии, называется волной.
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. Если направление колебаний частиц среды совпадает с направлением распространения волны, то волна называется продольной.
Если направление колебаний перпендикулярно направлению распространения, то волна называется поперечной.
Для возникновения поперечных волн необходимо, чтобы среда обладала упругостью на сдвиг. Поэтому поперечные волны существуют лишь в твердых средах, а в газах и внутри жидкости существуют только продольные волны.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (волновым фронтом).
Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
Волновую поверхность можно провести через любую точку пространства, т.е. их бесчисленное множество. Все частицы среды, образующие фронт волны, тоже колеблются в одинаковой фазе, таким образом, фронт волны – это одна из волновых поверхностей.
По форме волновой поверхности волны делят на плоские, сферические и цилиндрические. Положение волновой поверхности и волнового фронта в любой момент времени позволяет определить принцип Гюйгенса.
Каждая точка среды, до которой дошло колебание, сама становится источником вторичных полусферических волн, а огибающая всех этих вторич-
53

ных волн дает положение волнового фронта в последующий момент времени
(рис. 3.2).
Рис. 3.2
3.1.2. Уравнение бегущей волны
Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию координат ее положения равновесия и времени:
|
|
|
|
|
ξ = ξ(x, y, z,t). |
(3.1) |
|
|
|
|
|
Сначала найдем вид функции ξ в случае |
|
|
|
|
|
|
||
|
|
|
|
|
плоских гармонических волн (рис .3.3). |
|
|
|
|
|
|
Направим ось Х вдоль направления рас- |
|
|
|
|
|
|
пространения волны. Волновые поверх- |
|
|
|
|
|
|
||
|
|
|
|
|
ности в этом случае перпендикулярны |
|
|
|
|
|
|
оси Х и смещение ξ будет зависеть толь- |
|
|
|
Рис. 3.3 |
|
ко от х и t. |
|
|
|
|
Уравнение колебаний точек в плоскости х = 0 имеет вид: |
|
|||
|
|
|
|
ξ(0,t)= a cos(ωt + α). |
(3.2) |
|
Волновой фронт и волновые поверхности распространяются со скоро-
стью υ, которая называется фазовой скоростью. Колебания частиц в плоскости
х отстают по времени на τ = |
х |
от колебаний частиц в плоскости х = 0: |
|
|||
υ |
|
|||||
|
|
|
|
|
|
|
|
|
|
ωt − |
ω |
|
(3.3) |
ξ(х,t)= a cos(ω(t − τ)+ α)= a cos |
υ |
x + α . |
||||
|
|
|
|
|
|
|
54

Это и есть уравнение волны. «Мгновенная фотография» подобной волны изображена на рис. 3.4. С течением времени эта картина движется вдоль оси Х, поэтому волна называется бегущей.
Рис. 3.4
Те точки пространства, в которых ξ максимальна, называются гребнями,
а в которых ξ минимальна – впадинами.
Расстояние между соседними гребнями или соседними впадинами, или любыми двумя точками, фазы которых отличаются на 2π, называются длиной волны λ.
ϕ = 2π = ωυλ ,
λ = |
2πυ |
= |
υ |
= υТ . |
(3.4) |
||
ω |
|
ν |
|||||
|
|
|
|
||||
Длина волны – это расстояние, проходимое волной за один период колебаний.
Величина ωυ = k называется волновым числом, а вектор kr = k nr, где n -
единичный вектор нормали к волновой поверхности, называется волновым век-
тором.
ξ(х,t)= a cos(ωt − kx + α). |
(3.5) |
Если волна бежит в противоположном направлении (т.е. против оси Х), то уравнение волны имеет вид:
55
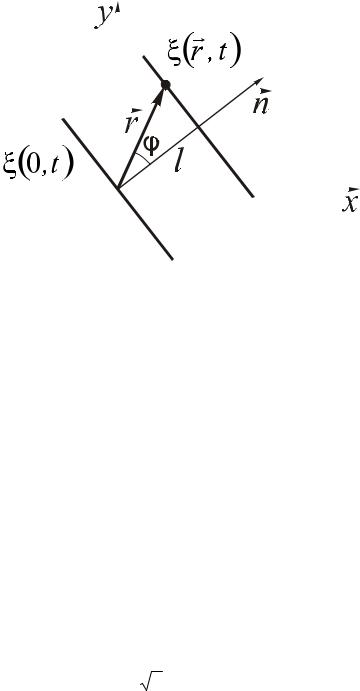
ξ(х,t)= a cos(ωt + kx + α). |
(3.6) |
||||||
Если направление распространения плоской волны не совпадает с осью Х |
|||||||
(рис. 3.5), то положение колеблющейся точки задается радиус-вектором |
r и |
||||||
уравнение волны имеет вид: |
|
||||||
ξ(rr,t)= a cos(ωt − krr + α). |
(3.7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.5
Если среда непоглощающая, то амплитуда плоской волны а одинакова во всех точках пространства. В поглощающей среде амплитуда волны убывает с расстоянием по закону
|
а = а е−γr , |
|
(3.8) |
|||
0 |
|
|
||||
где γ - коэффициент поглощения среды. Тогда уравнение волны будет |
|
|||||
ξ(rr,t)= a0е−γr cos(ωt − krr + α). |
(3.9) |
|||||
Уравнение сферической волны имеет вид: |
|
|
||||
ξ(rr, t)= |
а |
|
cos(ωt − krrr |
+ α). |
(3.10) |
|
|
||||||
|
|
r |
|
|
||
Уравнением цилиндрической волны будет выражение: |
|
|||||
ξ(rr,t)= |
а |
cos(ωt − krrr |
+ α). |
(3.11) |
||
|
||||||
|
|
r |
|
|
||
56

3.1.3. Волновое уравнение
Распространение волн в однородной изотропной непоглощающей среде описывается дифференциальным уравнением в частных производных, которое называется волновым уравнением. Полученное в предыдущем параграфе уравнение волны является решением волнового уравнения.
Рассмотрим плоскую волну, бегущую вдоль оси Х:
ξ(х,t)= a cos(ωt − kx + α).
Возьмем последовательно от этого выражения производные по координате х и времени t.
∂∂ξt = −aω sin(ωt − kx + α),
∂22ξ = −aω2 cos(ωt − kx + α), ∂t
∂∂ξx = −aω sin(ωt − kx + α),
∂2ξ2 = k 2a cos(ωt − kx + α). ∂x
Поделим вторые производные друг на друга
∂2 ξ |
|
|
|
k 2 |
|
ω2 |
υ2 |
|
|
|
1 |
|
|
||
∂2 |
2 |
|
= |
= |
|
= |
. |
(3.12) |
|||||||
ξ |
|
|
ω2 |
|
|
|
|||||||||
∂ |
|
|
ω2 |
|
|
|
|
|
υ2 |
|
|||||
∂t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом: |
|
|
|
∂2ξ |
= |
1 |
|
∂2 |
ξ |
. |
|
|
(3.13) |
||
|
|
|
∂х2 |
υ2 |
∂t |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Уравнение (3.13) называется одномерным волновым уравнением. В
общем случае волновое уравнение имеет вид:
∂2ξ |
+ |
∂2 |
ξ |
+ |
∂2 |
ξ |
= |
1 |
|
∂2ξ |
. |
(3.14) |
|
∂х2 |
∂y2 |
∂z |
2 |
υ2 |
∂t2 |
||||||||
|
|
|
|
|
|
||||||||
Решением уравнения (3.14) будет волна, распространяющаяся в про-
странстве с фазовой скоростью υ. Конкретный вид этой волны (плоская, сфери-
57

ческая и так называемая, амплитуда) будет зависеть от начальных и граничных условий.
3.1.4. Скорость упругих волн
Скорость упругих волн зависит от свойств среды. Упругие свойства среды определяются модулями упругости и в общем случае могут отличаться для продольных и поперечных волн.
Скорость продольных волн в твердой среде равна:
V = |
E |
, |
(3.15) |
прод ρ
где Е – модуль Юнга, ρ – плотность среды. Для поперечных волн эта скорость равна:
V = |
G |
, |
(3.16) |
поп ρ
где G – модуль сдвига.
Скорость поперечных волн в струне зависит от силы натяжения струны F и площади ее поперечного сечения S:
V = |
F |
. |
(3.17) |
стр |
S ρ |
|
Наконец, в газах скорость упругих волн определяется выражением:
Vгаз |
= γ |
р |
, |
(3.18) |
|
ρ |
|||||
|
|
|
|
где р и ρ – давление и плотность невозмущенного волной газа, а γ - показатель адиабаты (для воздуха γ ≈ 1,4).
Вопросы для самопроверки
1.Дайте определение волны.
2.Сформулируйте принцип Гюйгенса-Френеля.
3.Запишите уравнение бегущей волны.
58
3.2.Энергия упругой волны
3.2.1.Поток волновой энергии. Вектор Умова
Рассмотрим плоскую волну, бегущую вдоль оси Х.
ξ = a cos(ωt − kx + α). |
|
(3.19) |
||||||||||
Выделим в среде малый объем V. Учитывая, что масса этого объема |
||||||||||||
∂ξ |
и скорость |
υ = |
∂ξ |
|
|
|||||||
m = ρΔV, деформация ε = ∂ |
∂t , получим, что объем обладает |
|||||||||||
х |
|
|
|
|
|
|
|
|
|
|
|
|
кинетической Wк и потенциальной |
Wп энергиями, причем: |
|
||||||||||
|
|
|
|
|
1 |
|
∂ξ |
2 |
|
|
||
|
|
W = |
|
ρ |
|
|
|
V , |
(3.20) |
|||
|
2 |
|
|
|||||||||
|
|
|
к |
|
|
|
∂t |
|
|
|
||
|
1 |
|
2 |
|
|
1 |
|
∂ξ |
2 |
|
||
W = |
|
|
Еε |
|
V = |
|
|
Е |
V . |
|
||
2 |
|
2 |
|
|||||||||
п |
|
|
|
|
|
∂х |
|
|
||||
Учитывая, что модуль Юнга среды связан с фазовой скоростью волны υ соотношением E = ρυ2 , получим:
|
1 |
|
2 |
|
∂ξ |
2 |
|
W = |
|
ρυ |
|
|
|
V . |
(3.21) |
2 |
|
||||||
п |
|
|
|
∂х |
|
|
Полная энергия объема V определяется выражением: |
|
|
||||||||||||
|
|
|
|
|
1 |
|
∂ξ |
2 |
|
2 |
|
∂ξ |
2 |
|
W = W |
|
W |
|
|
|
|
|
V . |
||||||
+ |
= |
|
ρ |
|
|
+ υ |
|
|
|
|
||||
2 |
|
|
|
|||||||||||
к |
|
п |
|
|
∂t |
|
|
|
|
∂х |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда объемная плотность энергии равна: |
|
|
|
|
|
|
|
|||||||
|
W |
|
1 |
|
∂ξ |
2 |
|
2 ∂ξ |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
ω = |
V |
= |
|
ρ |
|
+ υ |
|
|
|
. |
|
(3.22) |
||
2 |
|
|
||||||||||||
|
|
|
∂t |
|
|
∂х |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив в эту формулу производные выражения (3.19) по х и t, полу- |
||||||||||||||
чим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = ρa2ω2 sin2 (ωt − kx + α). |
|
(3.23) |
|||||||||||
Можно сказать, что среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной.
59

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность.
Ф = |
dW |
. |
(3.24) |
|
|||
|
dt |
|
|
Размерность потока энергии в СИ – 1 Вт.
Плотностью потока энергии называется вектор, численно равный потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия, и направленный в направлении распространения волны.
r |
|
dФ r |
|
dW r |
|
||
j |
= |
|
n |
= |
|
n , |
(3.25) |
dS |
dS dt |
||||||
где nr – вектор единичной длины, направленный в направлении распростране- |
|||||||
ния волны. Плотность потока энергии характеризует перенос энергии в различных точках пространства.
Через площадку S (рис. 3.6) за время t |
будет перенесена энергия |
||||||||||||||||
W , заключенная в объеме цилиндра с основанием |
S и высотой υ t , где |
||||||||||||||||
υ - фазовая скорость волны. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6 |
|
|||||||||||
|
|
|
|
|
|
|
W = ω S υ t . |
(3.26) |
|||||||||||||||
Отсюда следует, что j = ω υ, а, учитывая, что направление фазовой ско- |
|||||||||||||||||||||||
рости совпадает с направлением переноса энергии, получаем: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j = ω υ. |
(3.27) |
|||||||
Вектор rj носит название вектор Умова.
60
Среднее за период значение вектора Умова называется интенсивностью,
I=  j
j .
.
3.2.2.Принцип суперпозиции волн. Стоячие волны
При распространении в упругой среде одновременно нескольких волн возникает их наложение, причем волны не возмущают друг друга! Колебания частиц среды оказываются векторной суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Это называют
принципом суперпозиции (наложением) волн.
Рассмотрим реализацию этого принципа в случае, когда две гармониче-
ские волны с одинаковой частотой ω и амплитудой а распространяются в противоположных направлениях оси Х:
ξ1 = а cos(ωt − kx) |
и |
ξ2 = а cos(ωt + kx). |
(3.28) |
Суперпозиция этих волн дает |
|
|
|
ξ = ξ1 + ξ2 = А cos kx cos ωt , |
(3.29) |
||
где А = 2а. Выражение (3.29) есть уравнение стоячей волны. Частота такой вол-
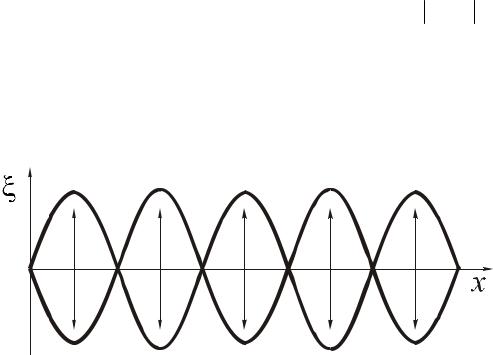
ны та же, а амплитуда зависит от координаты х. В точках, где cos kx =1 на-
блюдаются максимумы – пучности, а где cos kx = 0 - минимумы – узлы. Расстояние между соседними пучностями или узлами равно половине длины вол-
ны λ2 (рис. 3.7).
Рис. 3.7
61
Между двумя соседними узлами все точки среды колеблются синфазно
(т.е. в одной фазе), при переходе через узел фаза меняется на π, т.е. колебания по разные стороны от узла происходят в противофазе. Узлы как бы разделяют среду на автономные области, в которых гармонические колебания совершаются независимо. Никакой передачи движения от одной области к другой, а значит и перетекания энергии через узлы не происходит. Именно поэтому подобная волна и называется стоячей. Подобные волны существуют, например, в струнах всех струнных музыкальных инструментов.
3.2.3. Звуковые волны
Звук – это упругие волны, воспринимаемые человеческим ухом, т.е. в диапазоне частот от 20 Гц до 20 кГц.
Упругие волны с частотами, меньшими 20 Гц, называют инфразвуком, а с частотами больше 20 кГц – ультразвуком.
Звуки различают по высоте, тембру и громкости.
Высота звука определяется его частотой: чем больше частота, тем выше
звук.
Тембр звука определяется спектром частот, содержащихся в звуковой волне. Спектр может быть непрерывным (т.е. сплошным), такая ситуация ха-
рактерна для различных шумов. Спектр может быть дискретным ω1, ω2 и т.д. (линейчатый спектр). Состав этого спектра и определяет тембр звука. В линейчатом спектре низшая частота называется основной. Если остальные частоты находятся в определенном соотношении (т.е. кратны основной), то они называются гармониками. Такая ситуация соответствует музыкальному звуку.
Громкость звука – это величина слухового ощущения, позволяющая располагать все звуки по шкале от тихих до громких. При неизменной частоте и форме колебаний громкость растет с увеличением их интенсивности I, которая пропорциональна квадрату амплитуды волны. Чтобы вызвать ощущение звука, его интенсивность должна превышать некоторую минимальную величину – порог слышимости. Эта величина в области наибольшей чувствительности чело-
62
веческого уха (0,5 ÷ 5,0 кГц) составляет Iпор ≈10-12 Вт/м2. При интенсивности порядка 1 ÷ 10 Вт/м2 колебания перестают восприниматься как звук, вызывая в ушах ощущение давления и боли. Данное значение интенсивности называют
порогом болевого ощущения.
Громкость звука L измеряется в логарифмических единицах – децибелах
(дБ):
L =10 lg |
I |
, |
(3.30) |
дб I0
где I – интенсивность звука, а I0 – порог слышимости.
Например, шорох листьев, слабый шепот на расстоянии 1 м соответствует уровню в 10 дБ, шум в жилом помещении – 40 дБ, шум внутри трамвая – 70 дБ, сильные удары грома – 120 дБ, порог болевого ощущения – 130 дБ.
Вопросы для самопроверки
1.Что такое волна?
2.Когда возникают продольные и поперечные волны?
4.Что называется длиной волны?
5.В чем заключается физический смысл вектора Умова?
6.От чего зависит интенсивность звука? громкость и высота звука?
7.Что такое интерференция волн?
3.3.Электромагнитные волны
3.3.1. Физические следствия из уравнения Максвелла
Д. Максвелл, проанализировав предложенную им систему уравнений, описывающих электромагнитное поле, теоретически предсказал существование принципиально нового физического явления – электромагнитных волн – задолго до их экспериментального обнаружения. В своей теории Максвелл показал, что переменное магнитное поле порождает электрическое поле. Если электрическое поле – переменное, то оно, в свою очередь, порождает переменное магнитное поле и т.д. Таким образом, если возбуждать с помощью колеблющихся
63
зарядов переменное электромагнитное поле, то в окружающем эти заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся в пространстве. Этот процесс будет периодическим во времени и в пространстве и представляет собой волну. Экспериментально электромагнитные волны были открыты и изучены Г. Герцем спустя 10 лет после смерти Максвелла.
Электромагнитной волной называется переменное электромагнитное поле, распространяющееся в пространстве.
Рассмотрим уравнение Максвелла в дифференциальной форме для случая однородной нейтральной (ρ = 0), непроводящей (j = 0) среды с постоянными диэлектрической ε и магнитной μ проницаемостями.
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∂B = −μμ0 |
∂H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
rot E |
= − |
|
(1) |
|
|
divB = divH |
= 0 |
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂tr |
|
|
|
|
|
|
|
|
|
r∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(3.31) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
|
|
|
|
∂D |
= εε0 |
∂E |
|
(2) |
|
|
|
|
r |
|
|
|
|
|
r |
= 0 |
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
rot H = − |
|
∂t |
∂t |
|
|
|
|
|
|
divD = divE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Из уравнения (1) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
∂ |
|
|
|
∂E |
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
∂E |
x |
|
|
∂E |
z |
|
|
|
|
|
|
∂H y |
|
|
∂E |
y |
|
|
|
|
∂E |
x |
|
|
|
|
|
|
∂H |
z |
|
||||||||||||
Ez |
|
− |
|
|
|
y |
= −μμ |
|
|
|
H x |
, |
|
|
|
− |
|
|
|
|
|
= −μμ |
|
|
|
|
|
|
|
, |
|
|
|
− |
|
|
|
|
|
|
= −μμ |
|
|
|
. (3.32) |
||||||||||||||||||
|
|
|
|
|
|
|
|
∂z |
|
∂x |
|
0 ∂t |
|
|
|
∂x |
|
|
∂y |
0 ∂t |
|
||||||||||||||||||||||||||||||||||||||||||
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂z |
|
|
|
|
0 ∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
Аналогично из (2) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∂Нz |
− |
∂Нy |
|
= εε |
|
|
∂Еx |
|
, |
|
∂Нx |
− |
|
∂Нz |
= εε |
|
|
∂Еy |
|
, |
|
|
|
∂Нy |
− |
|
∂Нx |
= εε |
|
|
∂Еz |
. |
(3.33) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ∂t |
|
|
|
|
|
|
0 ∂t |
||||||||||||||||||||||||||||||||||||||||||
∂y |
|
|
|
|
∂z |
|
|
|
0 ∂t |
|
|
|
|
|
∂z |
|
|
|
∂x |
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
∂y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Уравнения (3) и (4) дают: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂E |
х |
+ |
|
∂Ey |
+ |
∂E |
z |
= 0 |
|
∂H |
х |
+ |
∂H y |
|
+ |
|
∂H |
z |
= 0 . |
|
|
|
|
|
(3.34) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂х |
|
∂y |
|
|
|
|
|
|
|
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
∂х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если взять первое уравнение (3.34), продифференцировать его по времени и учесть соотношение (3.34), то можно получить:
|
∂2 E |
|
1 |
|
∂2 E |
|
∂2 E |
|
∂2 E |
|
|
εε0 |
∂t2 |
x = |
|
|
∂x2 |
x + |
|
x + |
|
x . |
(3.35) |
|
|
|
|||||||||
|
|
μμ0 |
|
∂y2 |
∂z2 |
|
|||||
64

Аналогичные выражения можно получить и для проекций вектора Е на-
пряженности электрического поля и для напряженности Н магнитного поля. Тогда в векторной форме:
∂2 E ∂2 E ∂2 E |
|
∂2 E |
|
∂x2 + ∂y2 + ∂z2 |
= εμε0μ0 |
∂t2 . |
(3.36) |
∂2 H ∂2 H ∂2 H |
|
∂2 H |
|
∂x2 + ∂y2 + ∂z2 |
= εμε0μ0 |
∂t2 . |
(3.37) |
Подобные уравнения представляют собой волновое уравнение. Таким образом, переменное электромагнитное поле действительно распространяется в пространстве в виде волн, фазовая скорость которых равна:
|
|
υ = |
c |
, |
(3.38) |
|
|
|
εμ |
||||
|
|
|
|
|
||
где c = |
1 |
- скорость электромагнитных волн в вакууме. Оказалось, что |
||||
ε0μ0 |
||||||
|
|
|
|
|
||
с = 3 108 м/с, т.е. совпадает со скоростью света в вакууме. Поэтому Максвелл еще задолго до экспериментального подтверждения существования электромагнитных волн высказал гипотезу, что свет – это электромагнитные волны.
3.3.2. Плоская электромагнитная волна
Плоская электромагнитная волна является одним из решений волновых уравнений (3.36) и (3.37). Исследуем плоскую электромагнитную волну, распространяющуюся в нейтральной непроводящей однородной изотропной среде
(ρ = 0, rj = 0 , ε = const, μ = const). Направим ось Х перпендикулярно волновым
поверхностям. Тогда Еs и Нr , т.е. векторы напряженностей электрического и магнитного полей, не будут зависеть от Y и Z. В этом случае уравнения Максвелла (3.32) и (3.33) преобразуются к виду:
65
∂Ey |
= −μμ0 |
∂H z |
∂Нz |
= −εε |
|
|
∂Еy |
, |
|
|||||
|
|
0 |
|
|||||||||||
∂x |
∂t |
∂x |
|
|
|
|||||||||
|
|
|
|
|
|
∂t |
(3.39) |
|||||||
∂E |
|
|
|
∂H y |
∂Нy |
|
∂Еz |
|
|
|||||
z |
= μμ |
0 |
= εε0 |
. |
|
|
||||||||
|
|
|
|
∂x |
|
∂t |
|
|
||||||
|
|
∂t |
|
|
||||||||||
∂x |
|
|
|
|
|
|
|
|||||||
Из уравнений (3.39) следует, что, если первоначально было создано переменное электромагнитное поле с электрической компонентой вдоль оси Y
(Еry ), то возникает магнитная составляющая вдоль оси Z (H z ). Магнитная со-
ставляющая Нz приведет к возникновению компоненты Еy и т.д. При этом компоненты Еz и Нy не возникают. Аналогичные рассуждения можно провести для компонент Еz и Нy.
Выберем систему координат так, чтобы Еz = Нy = 0. Тогда волновое уравнение имеет вид:
|
∂2 Ey |
= |
εμ ∂2 Еy |
, |
|
|
|
|
|
|
|
||
|
∂x2 |
с2 |
∂t |
(3.40) |
||
|
|
|
||||
|
∂2 H z = |
εμ ∂2 H z . |
||||
|
|
|||||
|
∂x2 |
|
с2 |
∂t 2 |
|
|
Решением этих уравнений будет плоская волна, описываемая зависимо- |
||||||
стями: |
|
|
|
|
|
|
Ey = Em cos(ωt − kx + α1 ), |
(3.41) |
|||||
H z = Hm cos(ωt − kx + α2 ), |
(3.41) |
|||||
где ω - частота волны; k – волновое число; α1 и α2 – начальные фазы колебаний в точках с координатой х = 0. Если эти зависимости подставить в уравнение
(3.39), то можно получить, что α1 = α2, т.е. колебания векторов напряженностей электрического и магнитного полей в электромагнитной волне происходят с одинаковой фазой. Кроме того, для амплитуд этих векторов выполняется соотношение:
ε0εЕm2 = μμ0 Hm2 . (3.43)
66
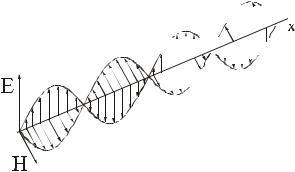
При этом в любой момент времени 




 векторы Е и Н перпендикулярны друг
векторы Е и Н перпендикулярны друг 











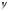 другу и направлению распространения
другу и направлению распространения 

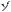

 волны, т.е. плоская электромагнитная волна – волна поперечная. На рис. 3.8 показана «мгновенная фотография» такой волны.
волны, т.е. плоская электромагнитная волна – волна поперечная. На рис. 3.8 показана «мгновенная фотография» такой волны.
Рис. 3.8
3.3.3.Свойства электромагнитных волн
Вотличие от упругих волн, распространение которых всегда происходит
вкакой-либо среде, электромагнитные волны могут распространяться и в вакууме, никакой среды для распространения электрического и магнитного полей не требуется. Разумеется, электромагнитные волны могут существовать и в среде.
Электромагнитные волны, распространяющиеся в однородной нейтраль-
ной непроводящей среде (ρ = 0, j = 0, ε = const, μ = const), являются попереч-
ными волнами. В предыдущем параграфе мы доказали это для плоской электромагнитной волны.
Электромагнитные волны, как и любые волны в линейной среде (т.е. в такой среде, где скорость распространения волны не зависит от энергии, переносимой волной), подчиняются принципу суперпозиции волн.
Результирующее возмущение в какой-либо точке линейной среды при одновременном распространении в ней нескольких волн равно сумме возмущений, соответствующих каждой их этих волн порознь.
В вакууме все электромагнитные волны распространяются с одинаковой скоростью, равной скорости света в вакууме с = 3 108 м/с. Скорость распространения электромагнитных волн в среде зависит от свойств самой среды. Если волна монохроматическая, т.е. в ней содержатся колебания одной единст-
67
венной частоты ω, то волна распространяется в среде с фазовой скоростью υ, связанной со скоростью света в вакууме соотношением
υ = |
с |
, |
(3.44) |
|
εμ |
||||
|
|
|
где ε и μ - диэлектрическая и магнитная проницаемости среды.
В случае, если волна не монохроматическая, то эту волну можно, в соответствии с принципом суперпозиции, представить в виде группы синусоидальных волн, т.е. – «волнового пакета». В общем случае каждая из синусоидальных волн волнового пакета может распространяться со своей скоростью. Тогда распространение волнового пакета характеризует скорость переноса энергии, которая называется групповой скоростью u . Если спектр частот волнового пакета не очень широк, то
u = |
dω |
= υ− λ |
dυ |
. |
(3.45) |
dk |
|
||||
|
|
dλ |
|
||
Если дисперсия среды (т.е. зависимость υ от λ) отсутствует, то групповая скорость волнового пакета равна фазовой скорости. С другой стороны, чем
dυ
сильнее дисперсия среды, т.е. чем больше значение dλ , тем сильнее различа-
ются фазовая и групповая скорости.
3.3.4. Поток энергии и интенсивность электромагнитных волн. Вектор Пойнтинга
Электромагнитные волны, так же как и упругие, переносят энергию. Для характеристики переноса энергии в разных точках пространства служит векторная величина, называемая плотностью потока энергии. Она численно равна энергии, переносимой через единичную площадь, перпендикулярную направлению переноса энергии в единицу времени.
Пусть электромагнитная волна распространяется в непроводящей среде.
Скорость волны при этом равна υ = |
с |
. Объемная плотность энергии элек- |
|
εμ |
|||
|
|
68

тромагнитного поля ϖw складывается из плотностей энергии электрического и магнитного полей:
w =wЕ + wН |
= |
εε0 Е2 |
+ |
μμ0 Н2 |
. |
(3.46) |
|
2 |
2 |
||||||
|
|
|
|
|
|||
Из п.3.3.2 известно, что в данной точке пространства векторы Еr |
и Н из- |
||||||
меняются в одинаковой фазе. Следовательно, соотношение
εε0 Еm2 = μμ0 Нm2
справедливо не только для амплитудных значений векторов Еr и Нr , но и для их мгновенных значений. Отсюда следует, что объемные плотности энергии электрического и магнитного полей волны в каждый момент времени одинаковы wЕ =wН . Формулу (3.46) можно преобразовать к виду
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w = |
εμ |
|
ЕН . |
(3.47) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поток энергии, переносимый волной через площадь dS: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dФ = |
dW |
, |
(3.48) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϖ |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где dW – энергия, переносимая волной |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
за время dt через площадку dS, т.е. это |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
энергия, заключенная в косом цилинд- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
ре, построенном на площадке dS, с об- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разующими равными |
υ dt (рис. 3.9). |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.9 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Видно, что: |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
(3.49) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dW =wdS υ dt cosα =w(υ dS )dt , |
||||||||||||||
где вектор площадки dS равен по модулю ее площади и направлению по нормали к площадке. В итоге поток энергии будет равен
|
r |
(3.50) |
|
dФϖ =w(υ dS )= ПdS , |
|
где вектор Пr |
- вектор плотности потока энергии, называемый в случае элек- |
|
тромагнитных волн вектором Пойнтинга. |
|
|
|
r |
(3.51) |
|
П =wυ. |
|
69

Модуль вектора Пойнтинга равен:
|
|
П =w υ =w |
c |
= |
εμ |
ЕН |
c |
= EH . |
(3.52) |
|
|
εμ |
с |
εμ |
|||||
|
|
|
|
|
|
|
|||
Векторы Еr |
и Нr |
взаимно перпендикулярны и образуют с направлением |
|||||||
распространения волны правовинтовую систему. Поэтому направление вектора
Еr × Нr совпадает с направлением переноса энергии, а модуль этого вектора равен Е Н. Следовательно, вектор плотности потока электромагнитной энергии
можно представить как векторное произведение Е на Н : |
|
|
|
П = Е× Н . |
(3.53) |
Данное выражение справедливо для всех сред, в том числе проводящих. |
||
Зная значение вектора Пr |
в каждой точке некоторой поверхности S мож- |
|
но рассчитать энергию, переносимую волной через эту поверхность: |
|
|
|
Ф = ∫ПdS . |
(3.54) |
|
(S ) |
|
Поскольку в электромагнитной волне векторы Е и Н периодически изменяются во времени, то и вектор Пойнтинга также меняется во времени. Физический смысл только некоторое среднее значение энергии, перенесенное волной за некоторый промежуток времени (не менее чем период одного колебания).
Скалярная величина I, равная модулю среднего по периоду значения век-
тора Пойнтинга, называется интенсивностью волны. |
|
I = П = Е× Н . |
(3.55) |
Размерность интенсивности в системе СИ – Вт/м2. По сути интенсивность характеризует среднюю энергию, перенесенную волной через единицу площа-
ди в единицу времени. Поскольку амплитуды векторов Е и Нr |
электромагнит- |
||||
ной волны связаны соотношением (3.43), легко показать, что: |
|
||||
I = |
1 |
|
εε0 |
Em2 , |
(3.56) |
|
|
||||
2 |
|
μμ0 |
|
||
70
т.е. интенсивность волны пропорциональна квадрату амплитуды колебаний вектора Еr поля волны.
3.3.5. Шкала электромагнитных волн
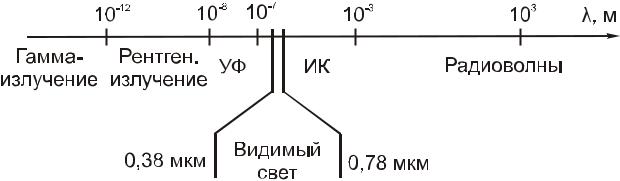
Электромагнитные волны излучаются колеблющимися заряженными телами. Диапазон частот (или длин волн) электромагнитных волн охватывает все возможные значения от 0 до ∞. По частоте или длине волны электромагнитные волны разделяют на следующие диапазоны.
Рис. 3.10
Самые длинные волны – это радиоволны, т.е. электромагнитные волны, длина которых более 1 мм (10-3 м). Радиоволны разбивают на несколько под-
диапазонов: длинные (λ > 1 км), средние (100 м < λ < 1 км), короткие (10 м < λ < 100 м), метровые (1 м < λ < 10 м), дециметровые (10 мм < λ < 1 м), сантимет-
ровые (1 см < λ < 1 см) и миллиметровые (1 мм < λ < 1 см). Радиоволны излучаются, главным образом, специальными радиотехническими устройствами.
Далее идет инфракрасное излучение (1 мм < λ < 0,78 мкм = 0,78 10-6 м).
Инфракрасное излучение испускается нагретыми телами.
Затем идет свет – электромагнитные волны, которые воспринимаются глазом человека. Границы оптического диапазона достаточно условны, чисто индивидуальны и меняются от человека к человеку, так же, как и границы слухового восприятия (хотя в случае света индивидуальный разброс значительно
71
ниже). Условно границы видимого диапазона оценивают как 0,38 мкм < λ < 0,78 мкм. Свет излучается как естественными источниками (звезды, нагретые тела, источники хемилюминесценции), так и созданными человеком (лампы, светодиоды, лазеры).
Еще меньшую длину волны имеет ультрафиолетовое излучение
(0,01 мкм < λ < 0,38 мкм). Ультрафиолетовое излучение есть в спектрах сильно разогретых тел (звезды, например) и специальных разрядных ламп (например, ртутные лампы искусственного загара).
Еще короче длина волны у рентгеновского излучения. Условно границы рентгеновского излучения определяют как 10-8 м < λ < 10-12 м. Это излучение возникает при взаимодействии заряженных частиц и фотонов с атомами вещества, например, при торможении электронов в металлах.
Самые короткие из известных человечеству электромагнитных волн – это
γ-излучение (λ < 10-12 м). Оно испускается возбужденными атомными ядрами и элементарными частицами при радиоактивных превращениях и ядерных реакциях.
Из всего этого широкого диапазона длин волн человек воспринимает лишь узкую часть спектра (0,38 мкм ÷ 0,78 мкм), однако 80 % информации человек получает именно посредством этих электромагнитных волн.
Вопросы для самопроверки
1.Что такое электромагнитная волна?
2.Как определяется фазовая скорость электромагнитных волн?
3.Чему равно численное значение вектора Пойнтинга?
4.От чего зависит интенсивность электромагнитной волны?
72
