8.2. Электростатическое поле

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1_toe-3-2009-12-22.pdf

Скачиваний:

Добавлен:

16.02.2016

Размер:

3.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

B	wI	,	(8.1.14)
	2 x

где магнитная проницаемость материала магнитопровода; w число

витков обмотки; I протекающий по обмотке электрический ток. Подставляя выражение (8.1.14) под знак интеграла в (8.1.13), для магнитного потока в случае постоянства магнитной проницаемости получим

r2	wI	wIh r2 dx			wIh		r
Ф	2 x hdx	2		x	2	ln r .
							2
r			r			1
1			1

расстоянии a от плоскости. Тогда его величина определяется из условия

8.2.1.Общие сведения об электростатическом поле

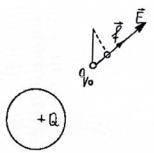
Электростатическим полем (ЭСП) называют электрическое поле неподвижных зарядов. Силовой характеристикой электрического поля является

напряженность E . Она определяется как отношение силы, действующей на пробный заряд, помещенный в электрическое поле, к величине этого заряда

(рис. 8.2.1)

Рис. 8.2.1. Пробный заряд в электрическом поле

	f
E q0		.
		.

Здесь под пробным зарядом понимаем заряд q0 положительного знака, настолько малый по величине, что он не искажает внешнего поля, в которое помещен.

Другой важной характеристикой электрического поля является вектор

электрической индукции (в диэлектрике его называют вектором электрического

смещения) D . Если во внешнее поле, созданное положительным зарядом Q, поместить две тонкие металлические пластины небольшого размера с изолированными ручками (рис. 8.2.2), то свободные или слабосвязанные со

своими атомами электроны переместятся влево. Левая пластина окажется заряженной отрицательно, а правая пластина из-за недостатка электронов окажется заряженной положительно. Как видим, пластины зарядились без какого-либо контакта с зарядом Q , т. е. вследствие электрической индукции. За

изолированную ручку мы можем вынуть из рассматриваемой области любую из пластин – другая останется и будет иметь положительный или отрицательный заряд. Описание этого явления производится с помощью характеристики, которую называют электрической индукцией. Поверхностная плотность заряда, наведенного на любой из пластин, D , а весь заряд на пластине Q S , где

S – площадь пластины.

Рис. 8.2.2. Смещение отрицательного заряда в электрическом поле

Если в пространство вблизи заряда Q поместить диэлектрик, например, неполярный (т. е. такой, атомы которого в отсутствие поля не обладают дипольным моментом – центры электронных оболочек и положительного ядра совпадают), то под влиянием заряда Q электронные оболочки атомов диэлектрика будут притягиваться к заряду Q – произойдет смещение отрицательного заряда (рис. 8.2.2). Описание этого явления производится с помощью характеристики, которую называют вектором электрического смещения.

Электрическое поле свободных зарядов, созданных внешними источниками и находящихся на электродах или в виде пространственного заряда, ослабляется действием связанных зарядов вещества, в котором эти

свободные заряды находятся (рис. 8.2.3). Фактическое результирующее поле E

обусловлено свободными и
связанными зарядами. При этом теорема Гаусса имеет вид
S EdS	1	(Qсвоб Qсвяз )	,	(8.2.1)
S EdS		(Qсвоб Qсвяз )	,

Рис. 8.2.3. Распределение электрических зарядов между двумя электродами

причем знак заряда Qсвяз	противоположен знаку заряда Qсвоб . Уравнение,
называе-		D
мое постулатом Максвелла, связывает вектор и свободный заряд Qсвоб.: .
	.	(8.2.2)
	.
Поэтому	sDdS Qсвоб

0 sEdS Qсвоб Qсвяз ,

откуда

Qсвоб =	0 EdS	–	Qсвяз =	0 EdS	–	0 PdS .
	s			s		s

Вектор, ответственный за образование связанного заряда, назвали вектором поляризации Р. С учетом предыдущего в однородных средах

S DdS S 0 EdS SPdS ,

откуда

D = εE – P ,

причем		0 r ; 0	= 8,85 10-12 Ф/м; вектор D	совпадает с вектором
	D = εE ;

E , вектор P им противоположен, т. е. численно

D = 0 Е + Р .

Как уже отмечалось, в поле неподвижных зарядов нет токов, значит, нет и вызываемого токами магнитного поля. Поэтому уравнение для электростатического поля имеет вид

rot E = 0.

(8.2.3)

Уравнение (8.2.3) формулируется следующим образом: «ротор (вихрь) электрического поля E в рассматриваемой области пространства отсутствует», что дает возможность продолжать: «следовательно, оно безвихревое и аналитически может быть описано некоторой скалярной потенциальной функцией», которую называют электрическим потенциалом . Следовательно, потенциал скорее математическое понятие, чем физическое. Тем не менее при выполнении расчетов часто забывают об абстрактном смысле потенциала и оперируют с ним как с физической величиной, понимая под потенциалом действительно физическую величину – напряжение между точкой, в которой вычисляют потенциал, и другой точкой, потенциал которой принимается равным нулю. Связь между напряженностью электрического поля E и потенциалом устанавливается с помощью выражений

	P
A =	Ed ,	A	= P Ed .		(8.2.4)
	A
Потенциал в точке А определяется как интеграл от E по dl					от точки А, в
которой хотим найти потенциал, до точки Р, потенциал в которой принят
равным нулю. Положение точек А и Р определяется расстоянием вдоль
некоторого пути, отсчитываемого от выбранного начала отсчета. Взяв
производную от обеих частей равенства (8.2.4) по переменному нижнему
пределу (точка А может находиться в произвольном месте), получим
Откуда		El =		.
Откуда		El =		.

		= E d Ed .			(8.2.5)

Таким образом, потенциал в произвольной точке А может быть найден либо с помощью определенного интеграла (8.2.4), либо с помощью неопределенного интеграла (8.2.5).

Из общей системы уравнений Максвелла для ЭСП используются три: вышеуказанное (8.2.3) и

divD ,	(8.2.6)
D E ,	(8.2.7)

которые в однородном поле приводятся к одному уравнению:

	divgrad		.

			(8.2.8)

При отсутствии зарядов в рассматриваемой области

divgrad 0 .	(8.2.9)

Уравнение (8.2.8) называют неоднородным уравнением Лапласа (в технических дисциплинах уравнением Пуассона), уравнение (8.2.9) – однородным уравнением Лапласа (в технических дисциплинах уравнением

Лапласа) для электростатического поля. Запишем									уравнения Пуассона и
Лапласа в прямоугольной		divgrad 2
системе координат, используя выражение.
Так как
	2		2		2			2	,
			x2 y2 z 2						,
			x2 y2 z 2
то уравнение Пуассона
2		2		2					,
x2		y2 z2							,
x2		y2 z2							(8.2.10)
									(8.2.10)
а уравнение Лапласа
2			2		2		0		.
x2			y2		z	2	0		.
x2			y2		z	2			(8.2.11)
									(8.2.11)

Интегрирование уравнений Пуассона или Лапласа позволяет найти потенциал в каждой точке поля (x, y, z), а затем, используя выражения (8.2.4, 8.2.5), а также

E = grad

(8.2.12)

и напряженность поля E . При интегрировании уравнений Пуассона и Лапласа встречаемся с необходимостью определения постоянных интегрирования, которые находятся из граничных условий, т. е. тех физических условий, которые существуют на поверхностях раздела двух сред: проводника и диэлектрика или двух диэлектриков.

8.2.2. Граничные условия при решении задач электростатики

Условия на поверхностях проводников

Внутрипроводников	EE 0;					(8.2.13)
Внутрипроводников	EE 0;
На поверхностипроводников		E Еn		;	E 0	,


			n
где En --и E - сответственно нормальная и			касательная			к поверхности
провод-ника составляющие вектора E .

1. Поверхность проводника представляет собой поверхность равного потенциала

const .

(8.2.14)

2. Величина вектора D (вектора электрической индукции или вектора электрического смещения) численно равна поверхностной плотности заряда:

D ,

(8.2.15)

т. е. весь заряд проводника сосредоточен на его поверхности, внутри проводника заряда нет.

Условия на поверхности раздела двух диэлектриков

1. Касательные составляющие вектора E на поверхности раздела двух диэлектриков (рис. 8.2.4,а) равны.

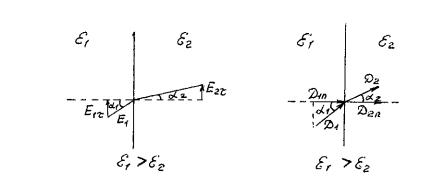
E1 E2 , .

E1 sin 1 E2 sin 2 ,

2. Нормальные составляющие вектора D диэлектриков (рис. 8.2.4,б) равны.

(8.2.16)

на поверхности раздела двух

D1n D2n ,
D1 cos 1 D2 cos 2 , .		(8.2.17)

а)

б)

Рис. 8.2.4. Составляющие электрической напряженности на границе раздела двух диэлектриков

3. Соотношение между углом падения и углом преломления линий электрического поля на границе раздела двух диэлектриков дается выражением

tg 1		1		r1		(8.2.18)
tg 2		2		r 2 .

Скачок нормальной составляющей напряженности электрического поля объясняется наличием на границе сред некомпенсированных связанных зарядов и равен

En2	En1		связ .
			0

В каждой точке поверхности заряженного тела напряженность определяется поверхностной плотностью свободных зарядов.

E	.

Величина вектора поляризации равна поверхностной плотности связанных зарядов:

P связ .

Потенциал на границе раздела двух сред изменяется непрерывно.

				1 2 .
	(8.2.19)
Производные от потенциала, взятые по нормали к границе раздела,
удовлетворяют равенству
	1		2
1		2		,
1	n	2	n	,

что соответствует выражению (8.2.17).

Теорема, доказывающая, что задача расчета ЭСП по уравнениям Лапласа и Пуассона с учетом граничных условий может быть решена единственным образом, называется теоремой единственности.

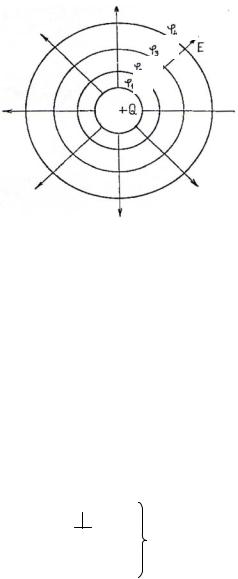
Для наглядности электрическое поле изображают с помощью картинок, называемых картинами поля. На картинах указывают линии вектора

напряженности E и линии равного потенциала . На рис. 8.2.5 изображено электрическое поле положительного заряда Q сферической формы. Поток

вектора E , создаваемый зарядом Q сквозь любую замкнутую поверхность S, по теореме Гаусса, равный

	EdS Q	,	(8.2.20)
S

разбит на трубки равного потока. Границы между трубками равного потока на рис. 8.2.5 есть линииE . Кроме того, на том же рисунке изображены линии равного

Рис. 8.2.5. Распределение электрического поля положительного заряда сферической формы

потенциала, т. е. следы на плоскости сферических поверхностей равного потенциала . Картина поля на плоскости строится так, чтобы удовлетворялись два правила:

1.Линии E и линии пересекаются под прямым углом.

2.Ячейки картины поля, образующиеся при пересечений линий E и , должны быть подобны друг другу:


Е

	а	const .	(8.2.21)
	n
расстояние между линиями		E ; n –	расстояние между линиями в
каждой	ячейке.
Цель	расчета поля: найти	значения	напряженности поля E и

электрического потенциала при заданной геометрии (расположение и форма заряженных тел) и граничных условиях. Последние могут быть трех видов:

а) заданы значения потенциала на границах поля (задача Дирихле); б) заданы значения напряженности поля на границах (задача Неймана) или, чтото же, задано распределение зарядов по поверхности проводящих тел;

в) заданы значения потенциалов на одних из границ, а на других напряженности (задачи со смешанными граничными условиями).

Ниже на примерах рассмотрены наиболее употребляемые и относительно простые методы расчета ЭСП.

8.2.3.Методы расчета электростатических полей

8.2.3.1.Расчет симметричных полей

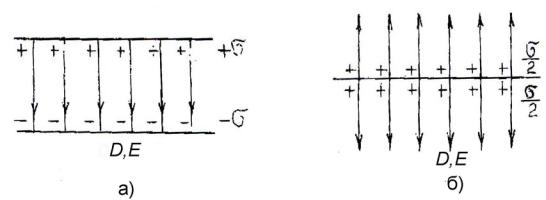
Задача 8.2.1. ЭП создано двумя тонкими, параллельно расположенными пластинами бесконечного размера. Поверхностная плотность заряда на одной из пластин + , на другой – Кл/м2. Найти напряженность поля между пластинами и снаружи пластин. Как изменится напряженность поля, если одну из пластин удалить? Для обоих случаев нарисовать картину поля.

Решение. В соответствии с граничным условием (8.2.13) весь заряд пластины сосредоточен на ее поверхности, обращенной к другой пластине. D ;

E D / ;

0 r ; r = 1. Распределение векторов D , E в пространстве между пласти-нами изображено на рис. 8.2.6,а.

Если одну из пластин удалить, ЭП окажется симметричным по обе стороны оставшейся пластины (авторы позволят себе сформулировать принцип симметрии: если нет никаких причин, которые нарушали бы возможную симметрию, она существует).

Рис. 8.2.6. Распределение векторов электрического поля в пространстве между пластинами

D		,	E =	D	.
	2			2	.
	2			2

Картина поля изображена на рис. 8.2.6,б.

Задача 8.2.2. В ЭП, образованное пластинами А и В, внесена пластина С из проводящего материала. Изобразить картину поля.

Решение. Картина поля изображена на рис. 8.2.7 по правилам построения картины поля (8.2.21). Там же показано распределение плотности заряда по пластинам. Результирующий заряд на пластине С отсутствует.

Рис. 8.2.7. Поле системы проводящих пластин

8.2.3.2. Расчет напряженностей полей наложением

Электрическое поле в воздухе, а также в подавляющем большинстве видов изоляции является линейным, т. е. линейна зависимость D E : D 0 r E , где

0 8,85 10 12 Ф/м, r = const. Для любой линейной среды применим метод наложения. С помощью этого метода ниже решены некоторые задачи.

Задача 8.2.3. Два одноименных точечных заряда Q и 3Q расположены на

расстоянии d друг от друга. Найти на прямой, проходящей через эти заряды, точку с нулевой напряженностью.

Решение. Обозначим E1 напряженность ЭП заряда Q , величиной E2 напряженность поля заряда 3Q . В точке, где E = 0, E1 = E2 и направлены в противоположные стороны, тогда

Q 3Q ,

4 R12 4 R22

где R1 , R2 – соответственно расстояния от искомой точки соответственно до зарядов Q и 3Q , причем R2 d R1 .

Q d R1 2 3QR12 ; R12 R1d 0,5d 0 ; R1 0,5d 0,75d .

Оставляя положительный корень, найдем R1 0,365d .

Задача 8.2.4. Рассчитать поле двухпроводной линии.

Решение. Пусть точки А и В – следы пересечения плоскости заряженными проволоками + и (рис. 8.2.8). Найдем значения напряженности поля Е и потенциала в произвольной точке М.

Рис. 8.2.8. Следы пересечения плоскости заряженными проволоками E1 1 – напряженность поля от заряженной проволоки + , направлена по

2 a

линии, соединяющей точку М с зарядом + .

E2		1	– напряженность поля от заряженной проволоки , направлена
	2	b
по

линии, соединяющей точку М с зарядом .

М m ~ АМВ, так как отношение длин двух сторон одного треугольникаb / a пропорционально отношению длин двух сторон другого треугольника

E1 / E2 :

E1a E2b		;	E1	b .
	2		E2
				a

Заключенные между сторонами b и а и сторонами Ml и lm углы равны, как углы между параллельными сторонами (рис. 8.2.8). Из подобия треугольников

E E c	=		c	.	(8.2.22)

1 b		2 ab

Найдем теперь потенциал в точке М. Согласно (8.2.22) потенциал в точке М от заряда +

'м 2 lnb const .

Потенциал в точке М от заряда

'м' 2 ln a const .

Потенциал в точке М от обеих заряженных проволок

м 'м 'м' 2 ln ba const .

Постоянную интегрирования найдем, считая, что потенциал точки, расположенный посередине между заряженными осями, равен нулю. Так как при этом

b / a 1; ln1 0 , то 0 = 0 + const; const = 0,

M		ln b / a .	(8.2.23)
	2

Выше был рассмотрен случай, когда радиусы проводов ( r0 ) много меньше расстояния между проводами ( r0 c ). Рассмотрим теперь более сложный

случай, когда расстояние между проводами двухпроводной линии соизмеримо с радиусом проводов. При этом, с одной стороны, поверхности проводов (проводящие металлические) являются поверхностями равного потенциала; с другой стороны, произойдет смещение противоположных по знаку зарядов на проводах друг к другу. Это приведет к тому, что так называемые «электрические оси» проводов (+ ; )* и их геометрические оси (O1 ,O2 )

сместятся (рис. 8.2.8,б).

Условием эквипотенциальности является условие b / a const , поэтому для точки 1 (рис. 8.2.10,б)

а для точки 2	c r0	x	const ,
	r0 x

c r0 x const . r0 x

Так как точки 1 и 2 принадлежат одному проводу и потенциалы их равны, то

c r0 x		c r0 x		,
r x			r x	,
0			0
откуда
x	c	c2	r02 .
x	2	4	r02 .
	2	4

Далее задача решается аналогично предыдущему случаю (когда геометрические и «электрические» оси совпадают).

___________________

*Т. е. весь заряд с поверхности цилиндра переносится на одну линию, при этом рассчитанное поле будет учитывать неравномерное распределение зарядов на поверхности провода (проводящего цилиндра): на части поверхности, обращенной к другому проводу, поверхностная плотность заряда будет больше, чем на удаленном. Перенесение заряда с поверхности цилиндра на его «электрическую ось» аналогично перенесению заряда шара в его центр.

8.2.3.3. Расчет напряженностей полей, используя уравнения Лапласа и Пуассона

Задача 8.2.5. Между двумя бесконечными параллельными плоскостями, отстоящими друг от друга на расстоянии d (рис. 8.2.9), равномерно распределены объемный заряд с плотностью в однородной изотропной среде с проницаемостью .

Найти распределение потенциала в среде (х) и напряженности поля Е(х).

Решение. Если совместить координатную плоскость уоz с левой пластиной, то потенциал окажется функцией только координаты х и уравнение Пуассона примет вид

			2
			x2		.
Тогда
	x C		;	(x)			x2 C x C		.
	x C			(x)			x2 C x C	2	.
x		1				2	1	2
x						2
Постоянные интегрирования			найдем		из	следующих соображений: заряд

распределен равномерно, значит, можно считать, что его количество по обе стороны от плоскости А-А одинаково.

Значит, потенциалы плоскостей 1, 2 равны между собой. Будем считать

их равными нулю. Тогда из граничных условий найдем C1 ,C2 .
1) х = 0; (0) = 0 0			0 C1 0 C2 = 0 ;					С2 = 0.
	2

2) х = d; (d) = 0 0 =				d 2	C d ;	С1=		d .
							2

		2			1

Рис. 8.2.9. Объемный заряд с плотностью в однородной изотропной среде Окончательно имеем

	x	=					x2	d x .
	x	=					x2	d x .
					2			2
Задача 8.2.6. С	помощьюE =					x		d .измерительного		зонда
установлено, что	распределение	x						2	потенциала	между
установлено, что	распределение								потенциала	между
пластинами плоского конденсатора подчиняется уравнению
	a(		b	2	x2 )			,
	a(		4		x2 )			,
			4

где а, b постоянная, х – координата, отсчитываемая от середины междуэлектродного промежутка (рис. 8.2.10). Найти распределение электрических зарядов в межэлектродном пространстве и заряды на поверхности пластин конденсатора.

Решение. Уравнение Пуассона в прямоугольной системе координат

2	2	2	.
x2	y2	z2

Так как по условию задачи потенциал не зависит ни от y, ни от z, то

2			.
x2

Пользуясь выражением для потенциала, найдем

x = 2ax ,

Рис. 8.2.10. Распределение электрических зарядов в межэлектродном пространстве

2	=	2a ,
т. е. объемный заряд x2	=	2a ,
т. е. объемный заряд x2		в межэлектродном пространстве распределен
равномерно. :
2 a

Для определения зарядов на пластинах конденсатора применим постулат Максвелла сначала для правой, а затем для левой пластины конденсатора.

Правая пластина:

			S Q	S .
Eds Q	;	En1 S En2	S Q	S .
S
Здесь S – площадь пластины,		En взята со знаком ( ), а En			со знаком (+),
		1			2

так как положительной считается нормаль, направленная во внешнюю от

ограничиваемого междуэлектродного пространства сторону в направлении оси

x. Так как En =0 (напряженность ЭСП в проводящей среде), то = En .

Значение En , т.

е. напряженность поля в межэлектродном пространстве,

найдем из выражения

grad

x 0,5d ad ,

откуда

Левая пластина:

ad .

Eds Q ; En2 S En1 S

Так как En

= 0, то = En .

grad

x 0,5d

ad ; ad .

Обе пластины заряжены отрицательно с поверхностной плотностью зарядаad . Разность потенциалов между пластинами конденсатора U 0 .

8.2.3.4. Методы расчета с использованием электростатических коэффициентов

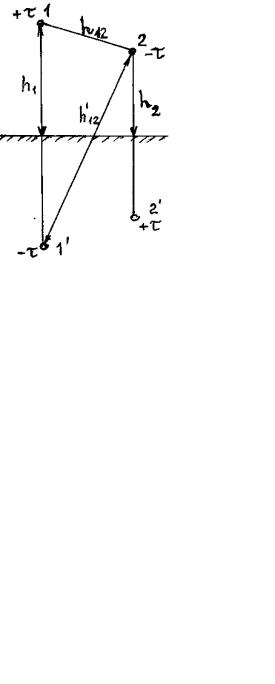
Задача 8.2.7. Двухпроводная линия над землей. Провода подвешены на разной высоте h1 и h2 над землей (рис. 8.2.11). Расстояние между проводами

h12 , линейные заряды проводов 1 = + ; 2 = . Радиусы проводов r0 <<y. Определить емкость между проводами на единицу длины.

Рис. 8.2.11. Схема двухпроводной линии над землей

Решение. Потенциалы проводов, записанные с помощью потенциальных коэффициентов, равны

	1 11 1 12 2	11			12 ,						(8.2.24)
	2 21 1 22 2	12				22 .					(8.2.25)
Для определения собственного потенциального коэффициента 11 нужно
положить 2	0 . В этом случае поле будет таким же, как поле однопроводной
линии над землей или как поле двухпроводной линии без земли.
					1						2h
	11	= 1							ln		r 1 .
						2		0
			1								0
Аналогично	22		2				1				2h2 .

		=			2
				2					0	ln r
											0

Для определения взаимного потенциального коэффициента 21 нужно, например, в уравнении (8.2.24) положить 2 0 . В этом случае потенциал в

точке расположения второго провода определится как потенциал в точке 2 от первого провода и его изображения:

						h'12						21 12				=						1				h'		.
	2 2 0 ln h12 ;											21 12				=					2				ln	h		.
																			2								12
																								0			12
Емкость между проводами на единицу длины (с учетом выражения																														11, 12
для ):
C					1								2 0												2 0				.
C							2			2h1			ln		2h2		2ln			h'12					4h h h2				.
1		2	11		22			12		ln			ln				2ln						ln			1	2	12
1		2	11		22			12				r0			r0					h12						1	2	12
																									2		'	2
																									2		'
																									r0	h12
Если провода подвешены очень высоко над землей, то																						h h					0,5h				,
тогда																						1			2				12
тогда						2 0					0						0
				C		2 0					0						0
							h122											d
							h122					h					ln	d	,
						ln r02			= ln			12		=			ln	r0	,
						ln r02			= ln			r		=				r0
												0

если принять h12 равным d.

8.2.4.Поля на различных расстояниях от источников

Вбольшинстве практических задач исследователя интересует определение поля не во всем пространстве, окружающем источники, а только в ограниченной конкретной области. Это обстоятельство значительно упрощает расчет без большой потери точности. Задачи, связанные с расчетом полей, при этом разделяются на два класса:

расчеты, целью которых является определение поля в непосредственной близости от поверхностей источников; такие задачи возникают, например, при расчете допустимых пробивных напряжений; нахождении условий, исключающих появление короны; выборе изоляционных расстояний и т. д;

расчеты, целью которых является определение поля в области, достаточно удаленной от источников; эти задачи связаны, например, с оценкой влияния одного элемента аппаратуры на соседние поля на значительных расстояниях от источников.

1) Потенциал ЭП проводника произвольной формы на расстоянии от его центра, большем или равном его основному габаритному размеру (Г), приближенно может быть принят равным потенциалу точечного (линейного в случае плоскопараллельного поля) источника. При этом максимальная погрешность не превышает 8 %. Это же положение можно отнести к градиенту потенциала (т. е. напряженности поля). Однако в последнем случае максимальная погрешность увеличивается до

12 % [2.4]. Таким образом, можно считать, что r 2Г.

	Q		;	Е =		Q	;
	4 r				4 r 2
		ln r	;	Е =				.

						2 r
2

Поскольку в практических задачах обычно задан потенциал проводника , заряд может быть найден через известную величину емкости проводника: Q =

Cφ.

2)Поле системы одноименно заряженных проводников в точках на расстоянии r (при r 2Г) от центра системы ( Г – наибольший габаритный размер системы) подобно полю точечного заряда, равного сумме зарядов системы и расположенного в его центре.

3)Поле системы произвольно заряженных проводников в точках, находящихся

вне области, границы которой отстоят от центра проводников на расстоянии r 2Г (Г – наибольший размер проводников), подобно полю соответствующих точечных зарядов.

Поля в непосредственной близости к заряженным телам рассчитываются методами, приведенными выше, а также другими более сложными методами.

8.2.5. Расчет емкости

Принято различать следующие виды емкостей: емкость уединенного проводника; емкость системы двух проводников (конденсатор); емкость системы, состоящей из многих проводников.

Емкостью уединенного проводника (предполагается, что все другие проводники удалены в бесконечность) называют отношение заряда Q этого проводника к его потенциалу , т. е.

C Q .

Емкость системы, состоящей из двух проводников, называют отношение заряда одного из проводников к разности потенциалов между ними. Поскольку это отношение может быть положительным или отрицательным (в зависимости от знаков выбранного заряда и разности потенциалов), то принято выражать эту емкость как

C		Q		.
C	1		2	.
	1		2

Общим случаем является система, состоящая из многих проводников. При этом, естественно, потенциал каждого проводника определяется не только его собственным зарядом, но также и зарядами всех проводников.

Методы расчета электрической емкости сводятся к методам расчета ЭП, как к перечисленным выше, так и другим, более сложным. Ниже в качестве справочного материала приведены наиболее распространенные формулы вычисления емкостей.

8.2.6. Расчет сил, моментов и энергии в электростатическом поле

Сила взаимодействия точечных электрических зарядов. Сила взаимодействия двух точечных электрических зарядов f определяется по закону Кулона:

f Q1Q22 ,

4 r

где Q1 , Q2 – электрические заряды, Кл; r расстояние между зарядами, м.

Сила f направлена по прямой, соединяющей точки, в которых сосредоточены заряды Q1 , Q2 .

Задача 8.2.8. Четыре заряда, помещенные в диэлектрик, располагаются в вершинах квадрата со стороной a =14,1 см (рис. 8.2.12,а). Определить силу,

действующую на		первый	заряд,		если Q 2 10 9	Кл; Q 4 10 9	Кл;
					1	1
Q 4 10 9	Кл; Q 2 10 9		; = 3	0	.
3		4		0

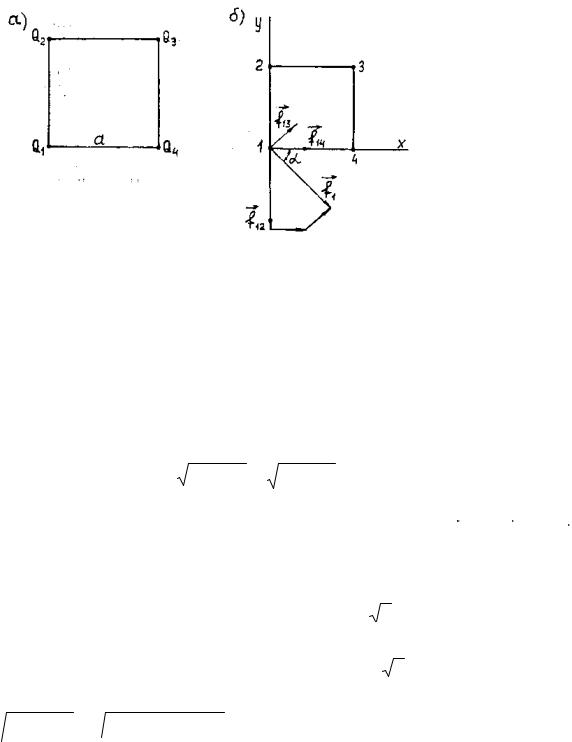
Решение. Задача решается с использованием принципа наложения механических сил, согласно которому суммарная сила, действующая на заряд, равна геометрической сумме действующих на него сил. На первый заряд действуют три силы – от второго, третьего, четвертого зарядов. Применяя закон Кулона, найдем эти силы:

Рис. 8.2.12. Четыре заряда, расположенных в вершинах квадрата в диэлектрике

															Q Q				2				2 10	9 4 10	9					1,21 10 6 H
							f		12						1				2														;
							f
														4				a2				4 3 8,85 10 12 14,12				10 4						Н
														4				a2				4 3 8,85 10 12 14,12				10 4
														Q Q									2 10	9 4 10	9							6 H
						f	13								1			3											0,603 10					;
						f																							0,603 10
													4					r 2					4 3 8,85 10 12 202			10 4							Н
													4					r 2					4 3 8,85 10 12 202			10 4
													Q Q				4						2 10	9 4 10	9					0,603 10 6
						f14								1			4																НH	;
						f14						4				a2						4 3 8,85 10 12 14,12				10 4							НH	;
												4				a2						4 3 8,85 10 12 14,12				10 4
																				r			a2 a2	2 14,12	20 см.
сил		Величину f1													находим, как геометрическую сумму f12 ,																	f13	,	f14
сил						(рис. 8.2.12,б). Аналитически ее можно найти по
проекциям:
f	1x	f	12x		f			14x			f				13x			0 0,603 10 6 0,603 10 6									2	1,030 10			6	H
f		f			f						f							0 0,603 10 6 0,603 10 6										1,030 10				H
																											2					Н;
																											2
f	1y	f		12 y		f				14 y			f			13 y					1,21 10 6 0 0,603 10 6							2		0,784 10 6 H
f		f				f							f								1,21 10 6 0 0,603 10 6									0,784 10 6 H
																											2							Н;
																											2

f f12x f12y 1,0302 0,7842 10 6 1,295 10 6 HН.

Сила взаимодействия заряженных тел. Сила взаимодействия заряженных тел определяется через энергию, запасенную этими телами в электрическом поле.

Из механики известно, что состояние любой системы тел как механической системы может быть описано с помощью так называемых обобщенных геометрических координат, число которых должно быть равно числу степеней свободы системы. К обобщенным координатам g относятся линейные перемещения тел по заданному пути, углы поворота вокруг некоторой оси, элементы поверхности тел, объемы и т. д. В соответствии с обобщенными координатами вводится понятие обобщенной силы f так, что dAмех f dg .

В зависимости от обобщенной координаты g имеет тот или другой смысл и обобщенная сила f. Так, если g – линейное перемещение, то f – обычная механическая сила; если g – угол поворота, то f – вращающий момент; если g – элемент поверхности, то f – поверхностное натяжение и т. д.

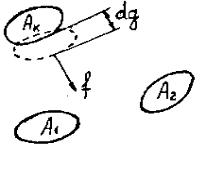
Предположим, что в произвольной системе, состоящей из n заряженных тел, все тела, кроме Ak , закреплены неподвижно. Тело Ak может перемещаться

под действием силы f, причем изменяется координата g (рис. 8.2.13). Тогда работа, затрачиваемая внешними источниками на изменение величины зарядов тел, обладающих потенциалами k , будет идти на приращение энергии dWe

системы зарядов, соответствующее изменению координаты g тела Ak , и расходоваться на механическую работу, совершаемую силой f при перемещении тела Ak :

Рис. 8.2.13. Произвольная система заряженных тел

	n	(8.2.26)
	k dQk dgWe fdg ,	(8.2.26)
	k dQk dgWe fdg ,

k 1

Последнее выражение отражает закон сохранения энергии. Возможны два случая: заряды всех тел остаются неизменными; потенциалы всех тел остаются неизменными.

В первом случае Qk const . Случай возможен, когда все тела после зарядки отключены от источников ЭДС, тогда на основе закона сохранения заряда заряды всех тел остаются неизменными, т. е. k d Qk = 0.

0 dgWe Qk const fdg,

	W		. .	(8.2.27)
f	e		. .	(8.2.27)
	g	Qk	const

Механическая работы совершается за счет внутренних запасов энергии в системе, энергия ЭП при этом убывает. За счет этой убыли и действует механическая сила.

Во втором случае k = const (все тела подключены к источникам с постоянными ЭДС). При изменении конфигурации системы меняются заряды тел. Энергия ЭП заряженных тел

	1	n
We	1	k Qk .
	2 k 1

Действительно, в самом простом случае плоского конденсатора с обкладками площадью S и расстоянием между обкладками l энергия в единице объема, гдепотенциал одной обкладки при заземленной другой; Q – заряд обкладки конденсатора; E – напряженность электрического поля; D – значение вектора электрической индукции. Тогда выражение (8.2.26) можно записать в виде

W 'e	ED	We ED lS				1	ElDS		1 Q ;
	2			2		2			2
		n			n
		k dQk			1 k dQk			fdg .
		k 1			2 k 1
Следовательно,
			1	n			dgWe k const ,
		fdg	1	k dQk			dgWe k const ,
откуда			2 k 1
откуда
			f		W			.	(8.2.28)
			f		e			.
					g
					g	k const

т. е. в случае постоянства потенциалов тел механическая сила, стремящаяся изменить координату g, равна отношению увеличения энергии ЭП (возникающего при подключении тел к источникам ЭДС) к изменению координаты.

Раздел 9. Электромагнитное поле постоянного тока 9.1. Электрическое поле постоянного ток 9.1.1. Методы расчета электрических полей

Внутри проводников, по которым протекает электрический ток, существует электрическое поле (ЭП). В изотропной среде напряженность поля связана с плотностью тока соотношением

J E ,

(9.1.1)

где γ удельная проводимость.

Выражение (9.1.1) называют законом Ома в дифференциальной форме. Действительно, умножив левую и правую часть (9.1.1) на сечение проводника Sпр, а также умножив и разделив правую часть (9.1.1) на длину проводника lпр, получим

I U	,	JSпр	Sпр	Elпр .	(9.1.1а)

R			l пр
Второе уравнение Максвелла в поле постоянных токов имеет вид
		rot E = 0.			(9.1.2)
В интегральной форме уравнение (9.1.2) записывается:
		U = 0; Edl 0 ,			(9.1.2 а)
		l

что представляет собой второй закон Кирхгофа, поэтому уравнение (9.1.2) называют вторым законом Кирхгофа в дифференциальной форме.

Линии тока в проводящей среде всюду непрерывны (принцип непрерывности электрического тока):

divJ = 0.

(9.1.3)

В интегральной форме это уравнение имеет вид

EdS 0 ;	I = 0,	(9.1.3 а)
S

что представляет собой первый закон Кирхгофа, поэтому уравнение (9.1.3) называют первым законом Кирхгофа в дифференциальной форме.

Таким образом, уравнения (9.1.1) – (9.1.3) представляют собой законы электрических цепей постоянного тока (постоянного, так как закон Ома в виде (9.1.1) учитывает только активное сопротивление проводника в отличие от цепей переменного тока, где необходимо также учитывать емкость конденсатора и индуктивность катушки. Поэтому задачи на расчет цепей постоянного тока, которые приводятся в разделе курса ТОЭ «Теория линейных электрических цепей постоянного тока», по существу, являются примерами расчета ЭП постоянных токов (здесь не рассматриваются).

Поле в диэлектрике, окружающем проводники с токами, характеризуется уравнениями:

rot E = 0; divD 0; D E .

Так как rot E = 0, то поле потенциальное, E = grad . Так как, divE 0 , то

		div grad =0;					2 0 .	(9.1.4)
В декартовой системе координат
	2			2		2	0 .	(9.1.5)

x2			y2		z 2

Уравнение (9.1.5) называется уравнением Лапласа.

Таким образом, в диэлектрике, окружающем проводники с токами, поле описывается тем же уравнением Лапласа, как и в ЭСП.

Граничные условия на поверхности проводник-диэлектрик в рассматриваемом поле отличаются от ЭСП. В ЭСП поверхность проводящего тела является поверхностью равного потенциала, линии напряженности

нормальны к поверхностям проводящих тел E = Еn. В рассматриваемом поле векторы напряженности имеют не только нормальную, но и тангенциальную составляющую Е (при прохождении тока по проводнику возникает падение напряжения U = Е l). Поэтому линии напряженности поля подходят к

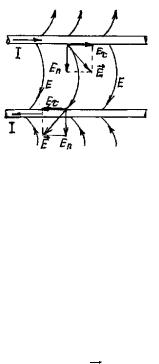
проводнику не под прямым углом (как в ЭСП), а под некоторым, отличным от прямого (рис. 9.1.1). Так обстоит дело, если рассматривать вопрос строго теоретически. Практически же обычно Е << Еn и касательной составляющей можно пренебречь. Действительно, пусть на расстоянии d = 10 cм друг от друга находятся два параллельных провода. Напряжение между ними U = 100 В. Плотность тока в проводе J = 5А/мм2. Провода медные = 58 м/Ом мм2.

Рис. 9.1.1. Размещение электрической напряженности вблизи проводников

E			J	5 0,086 B/м;
E			γ	5 0,086 B/м;
			γ	8
E	U 100 103 B/м;
n		d		0,1
		d		0,1
En		104		E En .
E

Поэтому при рассмотрении ЭП в диэлектрике, окружающем проводники с токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.

Решения, полученные при рассмотрении электростатических задач, можно использовать также при анализе ЭП внутри проводящих тел с постоянными токами или токами низкой частоты, так как между уравнениями ЭП в проводящей среде и уравнениями ЭСП существует аналогия, приведенная в табл. 9.1.1.

Таблица 9.1.1

Электрическое поле в проводящей Электростатическое поле среде

rot E = 0		rot E = 0
divJ 0		divD 0
J dS I	DdS D
S	S	( D = Q)
I = GU		D = CU
		D = CU

Где D поток вектора D сквозь некоторую поверхность S, равен части заряда заряженного тела (рис. 9.1.2). Согласно рис. 9.1.2 D1 = Q1 ; D2 = Q2 ; D3 =Q3 ; Q1 + Q2 + Q3 = Q – заряд тела 1.

Рис. 9.1.2. Электрическое поле в системе заряженных тел

Используя вышеприведенную аналогию, можно получить решение задач ЭП в проводящей среде на основе решений ЭСП и наоборот, если заменить:

, D J , C G , D I .

Аналогичны также и граничные условия на поверхности раздела сред в ЭСП и ЭП в проводящей среде (табл. 9.1.2)

Выводы, полученные на основе табл. 9.1.1 и табл. 9.1.2, позволяют моделировать экспериментально ЭСП электрическим полем в проводящей среде, используя для этого проводящую бумагу (если производится моделирование на плоскости) или электролитическую ванну (если производится объемное моделирование).

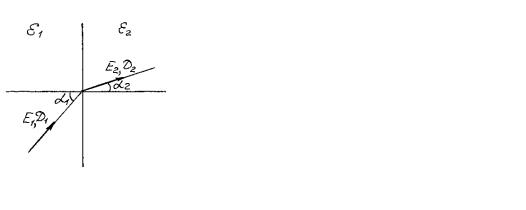
9.1.2. Электрическое поле в проводящей среде

Задача 9.1.1. Плоский конденсатор с многослойным диэлектриком имеет площадь обкладок S = 25см2 , толщины слоев d1 = 2 см, d2 = 3 см, d3 = 2 см и удельные проводимости в слоях: 1 = 10 10 1/Ом м; 2 = 1,5 10 10 1/Ом м; 3 =

10 10 1/Ом м. Определить сопротивление утечки и емкость конденсатора, используя метод электростатической аналогии.

Решение. Электрический ток проводимости в конденсаторе вследствие конечной проводимости диэлектриков одинаковый во всех слоях:

Таблица 9.1.2

ЭП

ЭП в проводящей среде

E1 E2

D1n D2n

J1n J 2n

tg 1

tg 2

I = JS,

так как S одинаково, то и J одинаково во всех слоях, поэтому

;

U E1d1 E2d2 E3d3

Проводимость утечки Gут = R1 , откуда

C		S		.
	d1 d2		d3
	1	2	3

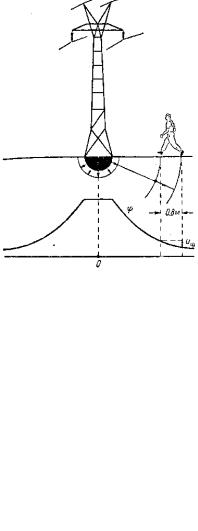
Задача 9.1.2. Полусферический заземлитель радиусом a погружен в землю вровень с ее поверхностью (рис. 9.1.5). Определить напряжение шага (шаговое напряжение) U Ш , под которым может оказаться человек, приближающийся к заземлителю. Ток I, протекающий через заземлитель, задан.

Рис. 9.1.3. Полусферический заземлитель

Решение. Поверхность полусферы в два раза меньше поверхности сферы, поэтому на произвольном расстоянии r от центра заземлителя

E	J	I	I
		S	2 r 2 .

Считая длину шага равной 0,8 м, найдем

	r 0,8	I	1	1	0,8I	1
Uш	Edr
				r 0,8	2 r(r 0,8) .
	r	2 r

При a = 50 см; = 10 2 1/Ом м; I = 1000 А; r = 3 м

Uш	105	0,33 0,264 1050	В
	6,28

при r = 5м U Ш = 445 В.

Если принять потенциал = 0 при r , то в остальных точках на поверхности земли, начиная от r = a , потенциал

				U p a ;
			2 r
				r
Uш	105	0,33 0,264 1050 В;
	6,28
На рис. 9.1.3 показана			кривая = f(r).

9.1.3.Энергия, силы и моменты в электрическом поле

9.1.3.1.Энергия системы заряженных тел

Простейшими примерами ЭП могут служить поля, связанные с неподвижными в пространстве (относительно наблюдателя) и неизменными во времени электрическими зарядами. Такие поля часто называют ЭСП, но в дальнейшем мы не будем пользоваться этим термином.

На практике, подразумевая энергию ЭП, созданного системой заряженных тел (зарядов), часто говорят об энергии именно таких тел, не уточняя, что эта энергия связана не столько с телами и их зарядами, сколько с самим полем этих заряженных тел.

Рассмотрим энергию ЭП уединенного заряженного проводящего тела. Для этого рассмотрим весь процесс зарядки этого тела от источника с нулевого заряда до состояния, в котором тело получило определенный заряд Q. Подсчитав работу, которую совершит источник энергии в течение всего процесса зарядки, и условившись, что этот процесс происходил без каких-либо потерь энергии, мы на основании закона сохранения энергии сможем принять найденную работу за энергию поля этого тела.

Предположим, что зарядка тела заключается в перенесении на него зарядов в бесконечности, где потенциал поля принимается равным нулю. Тогда за бесконечно малый отрезок времени dt, в течение которого телу был дополнительно сообщен заряд dQ, источник совершил работу

dA dQ ,

где φ – потенциал заряженного тела в рассматриваемый момент времени.

Всю работу, затраченную источником при сообщении телу заряда Q,

определим интегрированием бесконечно малой работы за весь период зарядки:

A dQ ,

т. е. от значения заряда, равного нулю, до его конечного значения Q.

Для того чтобы выполнить интегрирование, необходимо выразить подынтегральную функцию φ через независимую переменную Q. Сделать это нетрудно, прибегая к понятию потенциального коэффициента тела:

= Q .

Подставляя это выражение для потенциала под знак интеграла, получим

A QdQ 0,5 Q2

или, заменяя обратно произведение Q на φ, приходим к выражению для работы в виде

A 0,5 Q .

Энергия системы заряженных тел может быть определена как сумма энергий отдельных входящих в систему заряженных тел:

k n	(9.1.6)
We 0,5 k Qk .
k 1

Задача 9.1.3. Определить энергию заряженного конденсатора. Так как конденсатор представляет собой систему из двух заряженных тел, то энергия его ЭП представляется двумя слагаемыми:

We 0,5( 1Q1	2Q2 ) .
Заряды обкладок конденсатора всегда одинаковы по величине и
противоположны по знаку:
Q1 Q2	Q ,
то для энергии можно написать:
We 0,5( 1 2 )Q .
Принимая во внимание, что разность потенциалов обкладок представляет
собой напряжение между ними, т. е. напряжение U, до которого заряжен
конденсатор, для энергии конденсатора (энергии его ЭП) получим
W 0,5UQ 0,5CU 2 0,5(Q2 / C)		.	(9.1.7)
e		.	(9.1.7)

9.1.3.2. Объемная плотность энергии электрического поля

Каждый элемент пространства, занятого ЭП, несет в себе определенный запас энергии, обусловленный этим полем и зависящий от его интенсивности. В связи с этим вводят понятие об объемной плотности энергии ЭП, представляющей собой отношение энергии We, запасенной в данной области поля, к объему в этой области:

We We / v .

Если же оперировать областью бесконечно малого объема νd, с которой связан бесконечно малый запас энергии dWe, то мы аналогичным отношением определим понятие об объемной плотности энергии в данной точке поля:

(9.1.8) We dWe / dv .

Очевидно, что в равномерном поле понятия о средней объемной плотности энергии и объемной плотности энергии в данной точке совпадают.

Выражение для объемной плотности энергии ЭП можно вывести на примере плоского конденсатора. Этот пример удобен тем, что, во-первых, поле плоского конденсатора равномерно, а во-вторых, оно четко ограничено областью между пластинами (пренебрежем искажением поля у краев пластин конденсатора).

Представив энергию ЭП конденсатора в виде

We 0,5UQ ,

выразим его напряжение U через напряженность поля E и расстояние d между пластинами:

UEd ,

азаряд Q через поверхностную плотность σ заряда пластин, равную электрическому смещению D, и площадь s пластины:

Q s Ds,.
Тогда для энергии конденсатора имеем
We 0,5Ed Ds 0,5EDv ,	(9.1.9)
где ν объем пространства между пластинами.
Отсюда для объемной плотности энергии ЭП получим
We We / v 0,5ED ,.
D E
Пользуясь известным соотношением , последнее выражение можно
представить еще в двух формах:
W 0,5 E 2 0,5D2 / .	(9.1.10)
e

9.1.3.3. Общий метод расчета сил в системе заряженных тел

Рассмотрим систему, состоящую из n заряженных тел, соединенных с внешними источниками энергии, которые осуществляют их непрерывную подзарядку (рис. 9.1.4). В результате взаимодействия ЭП этих тел возникает ряд механических сил, действующих на отдельные тела. Сосредоточим внимание на одной из таких сил, например на силе q, приложенной к телу m, которое, допустим, имеет возможность перемещаться в направлении действия этой силы, в то время как все остальные тела жестко закреплены.

В течение бесконечно малого времени dt сила q переместит тело на бесконечно малое расстояние dg и совершит при этом элементарную работу qdg. Вместе с тем при движении m тела будет меняться картина ЭП системы, а в результате непрерывной подзарядки тел – возрастать его интенсивность. Поэтому в течение рассматриваемого времени dt произойдет изменение энергии ЭП системы на величину dWe. За это же время внешние источники, осуществляя подзарядку тел, совершат работу

Рис. 9.1.4. Система заряженных контуров с токами

k dQk

k 1	,

где φk потенциал k тела, dQk приращение его заряда Qk.

Все эти явления в совокупности описываются уравнением, отражающим закон сохранения энергии в системе заряженных тел в пределах времени dt:

k n
k dQk =	dWe	qdg ,,	(9.1.11)

k 1

согласно которому работа внешних источников энергии идет внутри системы на изменение запаса энергии в ЭП и совершение механической работы силой q .

Уравнение (9.1.11) справедливо только при условии, что подзарядка тел осуществляется без потерь энергии (по сверхпроводящим проводам), а в пространстве, где существует ЭП, не происходит необратимых процессов преобразования энергии.

Рассмотрим два частных случая. В первом случае предположим, что все тела отсоединены от источников. При этом изменений их зарядов происходить не может, и, следовательно, приращения зарядов равны нулю (dQk = 0). Тогда левая часть уравнения обращается в нуль, и оно приобретает вид

0 =	d gWe	+ qdg ,	энергии	(9.1.12)
причем индексом g у знака		дифференциала	энергии	ЭП

подчеркивается, что в рассматриваемом случае речь идет о частном дифференциале: когда заряды тел сохраняются неизменными, изменение энергии ЭП вызвано только изменением положения m тела, т. е. только за счет изменения dg его координаты g.

Из упрощенного уравнения (9.1.11) вытекает

	dgWe	W	(9.1.13)
q		e	,
q	dg	e	,
	dg	g

т. е. сила, действующая на одно из тел системы, равна по абсолютной величине и противоположна по знаку частной производной от энергии ЭП этой системы тел по координате, которая изменяется этой силой. При этом в процессе вычисления производной заряды тел следует считать постоянными.

Во втором случае положим, что все тела присоединены к источникам энергии и с их помощью потенциалы тел удерживаются неизменными. При движении одного тела системы, когда емкости между телами меняются, это возможно только при соответствующем изменении зарядов тел. Т. е. в этом случае приращения dQk зарядов уже нельзя считать равными нулю и в уравнении энергий (9.1.11) сохраняются все его члены. Однако возможно упростить равенство, используя выражение энергии системы заряженных тел:

k n
We 0,5 k Qk .
k 0
При неизменности потенциалов приращение энергии поля определится
приращением зарядов и выразится в виде
k n	(9.1.14)
dWe 0,5 k dQk .

k 0

Подставляя (9.1.14) в (9.1.11), получим

k n	k n
k dQk = 0,5	k dQk + qdg
k 1	k 0

или после приведения подобных членов

k n

0,5 k dQk = qdg

k 0

Возвращаясь к сокращенной записи приращения энергии ЭП, имеем

	dgWe = qdg ,
откуда	dgWe
	dgWe	W	(9.1.15)
q		e .
q	dg	e .
	dg	g

т. е. силу, действующую на одно из тел системы, можно вычислить путем частного дифференцирования энергии ЭП этой системы по изменяемой этой силой координате, полагая потенциалы тел неизменными. Но знак силы в этом случае необходимо принимать совпадающим со знаком производной.

Обе выведенные формулы удобно объединить в одну:

q	We	,	(9.1.16)

	g

(«+» – при const , « » - при Qi const ),

помня, что знак «плюс» берется, если при дифференцировании постоянными принимаются потенциалы, а знак «минус» - когда частная производная взята при условии постоянства зарядов.

Возможности расчета механических проявлений ЭП с помощью изложенного метода значительно расширяются, если в формуле (9.1.16) под величинами q и g понимать соответственно так называемые обобщенные силы и координаты. При этом под каждой парой «обобщенная сила обобщенная координата» следует понимать две физические величины, дающие при перемножении работу. Например, наряду с обычной механической силой f и длиной l, в качестве обобщенных пар можно рассматривать момент силы m и угол α, давление и объем, силу поверхностного напряжения и площадь. Из названных примеров наибольшее практическое значение имеют первые два, которые раскрывают возможность расчета не только линейных сил путем

дифференцирования по линейному размеру
f	We	,	(9.1.17)
	l

C ds .

но и моментов, действующих в различных электротехнических конструкциях, если прибегнуть к дифференцированию по угловым координатам этих конструкций:

m	We	.	(9.1.18)

9.1.3.4. Примеры расчета сил и моментов

Задача 9.1.4. Сила притяжения пластин плоского конденсатора может быть рассчитана путем дифференцирования энергии его ЭП по расстоянию d между пластинами, так как искомая сила стремится сблизить пластины, т. е. изменить координату d.

Используя выражение для энергии заряженного конденсатора в виде

We 0,5CU 2 ,

целесообразно выполнить дифференцирование, полагая потенциалы пластин конденсатора постоянными, т. е.

f We ,

так как при этом условии постоянным будет и напряжение U (оно равно разности потенциалов), фигурирующее в формуле энергии.

Если учесть, что

то						sU 2
f	W	= 0,5U	2	C	0,5	sU 2	.	(9.1.19)
f	e	= 0,5U		d	0,5	d 2	.
	d			d		d 2

Отрицательный знак результата показывает, что искомая сила стремится уменьшить координату d, т. е. сблизить пластины, что соответствует хорошо известному явлению притяжения разноименно заряженных тел.

9.2. Магнитное поле постоянного тока 9.2.1. Методы расчета магнитных полей

Уравнения магнитного поля (МП) постоянных токов, как это следует из общей системы дифференциальных уравнений ЭМП, имеют вид

rot H J ,	(9.2.1)
div B =0 ,	(9.2.2)
B H .	(9.2.3)

В соответствии с уравнением (9.2.1) МП является вихревым. Для его расчета используют математическое понятие, которое называют векторный

магнитный потенциал A . Это такая величина, которая плавно меняется от

точки к точке, ротор которой равен величине магнитной индукции B :
B = rot A .	(9.2.4)
Подстановка (9.2.4) в (9.2.2) дает выражение, тождественно равное нулю:

div rot A = 0.

Записав последнее выражение с помощью оператора «набла», имеем

divrot A = A скалярное произведение вектора на вектор, равный

векторному произведению A , что, как следует из рис. 9.2.1, всегда равно нулю (скалярное произведение двух векторов равно произведению их значений,

умноженному на косинус угла между ними). Угол между векторами и A по определению равен 90 , косинус этого угла равен 0.

Рис. 9.2.1. Скалярное произведение двух векторов Умножим обе части выражения (9.2.1) на величину :

rot H J .

Тогда в однородном поле при = const

rot H J ; rot B J ;

rotrotA graddivA 2 A J .				(9.2.5)
Как отмечалось выше, функция A непрерывна, т. е.
	div A =0.
Выражение (9.2.5) теперь можно представить в виде
	2 A J .			(9.2.6)
Выражение (9.2.6) представляет собой уравнение Пуассона			для	векторного

магнитного потенциала	A , аналогично уравнению	для	электрического
потенциала . Величина	A есть вектор, поэтому (9.2.6)	можно представить в

виде трех уравнений для компонент A :
2 Ax	J x ;
2 A J		y ;	(9.2.7)
y
2 Az	J z .

Решение уравнений (9.2.7) с учетом граничных условий в МП (см. ниже) позволяет найти величину индукции B и напряженности H МП.

Выражение магнитного потока через векторный магнитный потенциал

Магнитный поток Ф, пронизывающий какую-либо поверхность S, равен

Ф BdS.

С учетом (9.2.4)

Ф rotAdS.

По теореме Стокса

rot AdS Adl ,

	S
	откуда
	Ф Adl .	(9.2.8)
		(9.2.8)

Кроме того, что МП описывается векторным магнитным потенциалом A , в области, где нет токов, его также можно описать с помощью скалярного

магнитного потенциала м (по аналогии с тем, как ЭП описывается скалярным электрическим потенциалом ).

Другими словами, поскольку

rot H 0,

то

Hgrad м .

Сучетом (9.2.2) и (9.2.3) в однородном поле при = const

div B = div H = div H = 0;
		div H = 0.			(9.2.9)
divgrad			м	0;
			м
	2
	2	м 0.			(9.2.10)
		м 0.			(9.2.10)

Т. е. скалярный магнитный потенциал подчиняется уравнению Лапласа, которое в проекциях на оси прямоугольной системы координат записывается в виде

2 м	2 м	2 м	.
x2	y2	z2	0
			(9.2.11)

Граничные условия на поверхности раздела двух магнитных сред

Из выражения (9.2.9) находим
H1 = H2 ,	(9.2.12)
а из (9.2.2) соответственно
В1n = B2n,	(9.2.13)

где H1 , H2 касательные составляющие векторов H к границе раздела сред

(рис. 9.2.2);

Рис. 9.2.2. Граничные условия на поверхности раздела даух магнитных сред

В1n, B2n нормальные составляющие векторов B . Из рис. 9.2.2 также следует, что

H1 sin 1 H 2 sin 2 ;

B1 cos 1 B2 cos 2,

откуда

tg 1 tg 2 ;

1 2

tg 1		1 .
tg 2		2	(9.2.14)

Следствие:

1. Под каким бы углом линии магнитной индукции не входили из воздуха в ферромагнитную среду, внутри ферромагнитной среды они будут параллельны поверхности среды. Действительно, магнитная проницаемость воздуха 1 = 0. Магнитная проницаемость ферромагнетика, для примера, 2 = 104 0, тогда

	tg 1	1		0		1	.
	tg 2	2		104 0	104		.
Пусть 1 = 0,5 ,	tg 1 = 0,009		0,01, тогда			tg 2 =		104 0,01 = 100, что
соответствует 2 = 89,5 .

9.2.2. Закон полного тока. Скалярный магнитный потенциал

Задача 9.2.1. По длинному прямолинейному проводу радиусом R протекает постоянный ток I. Найти напряженность МП внутри и вне провода.

Решение. При постоянном во времени токе плотность тока по сечению провода есть величина постоянная:

J I 2,

при r R

Hdl Ir .	H 2 r	I	r 2 ;
		R2
r

H 2 IR2 r;

при r R

I = 2 rH ;	H	I	.

		2 r

Задача 9.2.2. Длинный прямолинейный провод имеет кольцевое сечение с радиусами R1 и R2 . По проводу протекает постоянный ток I. Построить кривую

H(r), где r расстояние от точки 0 на оси провода до произвольных точек областей 1, 2, 3 (рис. 9.2.3).

Рис. 9.2.3. Распределение магнитной напряженности от провода кольцевого сечения

Решение:

область: r < R1 , H = 0.

область: R1 r R2 ,

J – плотность тока;

I r 2 R12

2 rH

r 2 R12 .

2 R22 R12

R22 R12

;

область: r R2 , 2 rH = I.

2 r

График H(r) построен на рис. 9.2.3.

9.2.3.Векторный магнитный потенциал

9.2.3.1.Расчет поля с помощью векторного потенциала

Если отвлечься от временных изменений любого вида, т. е. в уравнениях Максвелла считать, что t 0 , но учитывать МП постоянных во времени токов, получим основные уравнения электродинамики стационарных токов:


rotH , rotE 0 , divB 0 , divD .		(9.2.15)
В этом случае уже существует связь между электрическими и магнитными
величинами, выражаемая уравнениями
	E , rotH E .	(9.2.16)
Математически задача состоит в определении вихревого поля без
источников по его вихрям. Уравнение divB 0 дает возможность выразить B
через векторный потенциал:
	B rotA.

Вектор H также принято определять через векторный потенциал. Но более

логично считать, что векторным потенциалом определяется именно векторB .

Действительно,

равенство

divB 0 справедливо всегда, тогда как равенство

divH 0 выполняется только в однородной среде.

можно

определить

из

уравнения

rotH после его

Вектор A

преобразования:

rotrotA graddivA A .

(9.2.17)

, получим

Полагая divA 0

A .

(9.2.18)

Для конечной области, ограниченной поверхностью a, имеем

A 1

da.

n r

4 V

4 a

Распространяя интегрирование на всю область, в которой 0 , получим

dv .

4 V r

(9.2.19)

С помощью векторного потенциала A может быть рассчитан магнитный поток, сцепленный с замкнутым контуром, ограничивающим поверхность a:

Bda rotAda .

a a

Но по теореме Стокса

rotAda Adl

a L

линейный интеграл векторного потенциала по замкнутому контуру равен магнитному потоку, сцепленному с этим контуром.

Как было показано, векторный потенциал A играет принципиально ту же

роль для МП (и других вихревых полей), как скалярный потенциал Э для ЭСП.

На практике, однако, векторным потенциалом пользуются гораздо реже. Это объясняется тем, что для измерения разности электрических потенциалов существуют простые измерительные приборы (для измерения векторного потенциала приборов не существует), а также и тем, что эта разность потенциалов непосредственно участвует в выражении мощности, которая играет большую практическую роль. Кроме того, в практических задачах

непосредственно виден смысл граничных значений Э, которые задаются очень просто, в то время как в МП существующие для A граничные условия

лишены такой		наглядности и	должны	быть определены через граничные

условия для H		и B .
	Сравнивая уравнения, связывающие B и , с уравнениями, связывающими
A и B :
		rotB 0 ,	rotA B ,	divB 0 , divA 0,

приходим к следующему заключению: если распределение магнитной индукции при данном распределении тока заменить фиктивным

распределением плотности тока f , то фиктивная магнитная индукция Bf ,

соответствующая такому распределению тока, совпадает с искомым векторным потенциалом (рис. 9.2.4).

Смысл приведенного вывода заключается в том, что он позволяет найти качественную картину, которая может быть полезна для отыскания количественных результатов.

Рис. 9.2.4. Распределение МП около кругового кольца с током

9.2.4. Метод зеркальных отображений

Бесконечно длинный провод с током I расположен параллельно плоской поверхности раздела двух однородных сред с магнитными проницаемостями µ1 и µ2 на расстоянии a от этой поверхности. Требуется рассчитать поле в обеих средах.

Эта задача с помощью метода зеркальных изображений может быть сведена к двум простым (рис. 9.2.5,а, б, в). При этом величину и направление фиктивных токов I1 и I2 можно получить, исходя из условий на поверхности

Рис. 9.2.5. Применение метода зеркальных отражений

раздела Ht1 Ht 2 и Bn1 Bn2 . Однако выражения для этих токов можно записать и на основе подобия плоскопараллельных ЭП и МП, если в соответствии с табл. 9.2.1 в выражениях для линейных зарядов заменить на I и

на 1/ .

Тогда

I1	1		2		I ;	I2	2 1		I .
		1		2			1	2
									(9.2.20)

Отсюда видно, что при µ2 > µ1 ток I1 имеет то же направление, что и ток I; при µ1 > µ2 обратное. Направление тока I2 всегда совпадает с направлением тока I. Соответствие магнитных и электрических величин плоскопараллельных полей приведены в табл. 9.2.1.

Таблица 9.2.1

ЭП				E	D		U
				E	D			C
МП	Jz	Az	1/	B	H	I	Ф	L 1

Табл. 9.2.1 получена на основе следующих соображений. Плоскопараллельное МП может быть создано в том случае, когда векторы плотности тока во всех точках параллельны между собой. Если в декартовых

координатах вектор плотности тока J имеет составляющую только вдоль оси z,

то и вектор A (векторный магнитный потенциал) будет иметь составляющую только вдоль этой оси и уравнение Пуассона в этом случае является скалярным:

		2 A	2 A		J z
		z		z	J z
		x2		y2			.
							.
Сопоставляя	это	уравнение			с	уравнением
плоскопараллельного электрического поля
		2		2
		x2		y2			,
							,

можно видеть, что при аналогичном распределении токовx, y решения будут аналогичны.

Пуассона для

J z x, y и зарядов

9.2.5. Силы, моменты и энергия в магнитном поле

Силы взаимодействия постоянного магнитного поля с движущимися частицами и токами. Сила, действующая на заряженную частицу при движении ее в магнитном поле (Сила Лоренца)

f Q v B ,

(9.2.21)

где Q – заряд частицы; v скорость ее движения; B вектор магнитной индукции в точке, где находится частица.

Сила взаимодействия между параллельными проводами с током

f	B I		l 0 I1 I		l
	1	2	2 d	2	(9.2.22)
при условии d<<l. Здесь	B1 – магнитная индукция на оси второго провода от
тока I1 ; I1 – ток в первом проводе; I2				– ток во втором проводе; l длина

проводов; d расстояние между осями проводов.

Если токи в проводах направлены одинаково, провода притягиваются. Если токи в проводах направлены в разные стороны – провода отталкиваются.

Задача 9.2.3. Расстояние между проводами d = 10 см (рис. 9.2.6). Токи в проводах I1 = 1000 А, I2 = 500 А направлены в одну сторону. Длина проводов 1 м. Определить магнитную силу взаимодействия f.

Рис. 9.2.6. Взаимодействие двух линейных проводников с токами

Решение:

	I	I	2	0	l	1000 500 4 10	7 1
f	1		2	0				=1Н.
f	2 d					2 0,1		=1Н.
	2 d					2 0,1

Силы в магнитном поле, действующие на помещенные в них тела.

Механическая работа и приращение энергии МП совершаются за счет той части

	n
энергии	ek ik dt источников, которую последние отдают в цепи
	k 1
		n
за вычетом тепловых потерь		ik2 Rk dt		, т. е. за счет части энергии
		k 1
так как	n	n		n
	ek ik dt =	ik2 Rk dt	+	ik d k,	.
	k 1	k 1	+	k 1	.

ik d k,

k 1

dWм 12 ik d ,k.

Последнее выражение получится, если уравнение равновесия в цепи, содержащей активные сопротивления и индуктивности, домножить на ik dt :

ek ik Rk d k .
dt
Таким образом,	(9.2.23)
n	(9.2.23)
ik d k fdx dWм .

Всоответствии со сказанным первое слагаемое выражения (9.2.33) – механическая работа (сила действует в направлении x), второе – приращение энергии МП, откуда

ik d k dWм

f	k 1		.
		dx

Из последнего выражения вытекают два важных случая.

1. Перемещение под действием силы f происходит таким образом, что потокосцепление контуров остается неизменным (при k = const d k = 0):

f				dWм
f		dx			,
или в общем случае
	W				,	(9.2.24)
f			м		,	(9.2.24)
		g		ψ = const

где g – обобщенная координата.

Механическая работа совершается за счет убыли энергии МП.

2. Перемещение происходит так быстро, что токи в контурах не успевают измениться. Так как

Wм 12 ik k

и dWм 12 ik d k ,

то в соответствии с (9.2.33)

ik d k fdx 12 ik d k ,

откуда

	ik d k	1	ik d k			1	ik d k	dWм
f		2				2		dWм
f	dx						dx	dx ,
	dx						dx	dx ,
или в общем случае
			W			.		(9.2.25)
	f			м		.		(9.2.25)
			g		i = const

Выражение (9.2.25) отличается от (9.2.24) лишь знаком.

Формулы (9.2.24), (9.2.25) для определения механической силы в МП аналогичны формулам для расчета механической силы в ЭП.

9.2.6. Магнитное поле в веществе

Если в МП, образованное током в проводах, внести то или иное вещество, тогда поле в веществе будет

B B0 B' ,

где B0 магнитная индукция внешнего поля, созданного током в проводах,

B' магнитная индукция, обусловленная намагничиванием вещества, B результирующая магнитная индукция в веществе.

В настоящее время установлено, что молекулы многих веществ обладают собственным магнитным моментом, обусловленным внутренним движением зарядов. Каждому магнитному моменту соответствует элементарный круговой ток, создающий в окружающем пространстве МП. При отсутствии внешнего МП магнитные моменты молекул ориентированы беспорядочно, поэтому обусловленное ими результирующее МП равно нулю. Равен нулю и суммарный магнитный момент вещества. Если рассматриваемое вещество поместить во внешнее МП, то под действием этого поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении и вещество намагничивается – его суммарный магнитный момент становится отличным от

нуля – возникает поле B'.

Часть веществ в отсутствие внешнего МП не имеют магнитного момента. Внесение таких веществ во внешнее поле индуцирует элементарные круговые токи в молекулах, и молекулы, а вместе с ними и все вещество, приобретают магнитный момент, что также приводит к возникновению поля B .

Большинство веществ при внесении в МП намагничивается слабо (парамагнетики), а некоторые даже приобретают вектор намагниченности J ,

обратный внешнему полю B0 (диамагнетики). Вещества, используемые в

электротехнических устройствах, можно условно разделить на два класса: ферромагнетики и неферромагнетики. Ферромагнетики намагничиваются сильно, неферромагнетики практически не намагничиваются. Например, медь

диамагнетик,	ее	магнитная проницаемость r 1, но	незначительно:	1
r 10,3 10 6 ,	т.	е. практически r 1. Алюминий	парамагнетик,	его

магнитная проницаемость r 1, но также незначительно: r 1 23 10 6 , т. е. практически r 1.

К ферромагнетикам относят железо, сталь, никель, кобальт, многие их сплавы и др. Относительная магнитная проницаемость ферромагнетиков достигает очень больших величин (для сплава супермаллой r = 800000).

Физическую природу ферромагнетизма удалось понять только с помощью квантовой механики. При определенных условиях в кристаллах могут возникать так называемые обменные силы, которые заставляют магнитные моменты электронов устанавливаться параллельно друг другу. В результате возникают области (размеры 1–10 мкм) спонтанного, т. е. самопроизвольного намагничивания – эти области называют доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определенный магнитный момент. Направления этих моментов для разных доменов различны, поэтому при отсутствии внешнего поля суммарный магнитный момент вещества равен нулю и вещество в целом является ненамагниченным.

При внесении вещества во внешнее МП домены, ориентированные по полю, растут за счет доменов, ориентированных против поля. Такой рост в слабых полях имеет обратимый характер. В более сильных полях все домены ориентируются в направлении внешнего поля, до тех пор, пока направления магнитных моментов доменов не совпадут с направлением внешнего поля (произойдет насыщение). На рис. 9.2.7 изображены кривая намагничивания ферромагнитного материала и соответствующая ей зависимость (H).

Уравнения МП постоянных токов (9.2.1) (9.2.2) можно рассматривать как

законы магнитных цепей. Действительно,
lм		Hlм	U м	(9.2.26)
B H BSм HSм lм	Ф	lм	Rм .

Sм

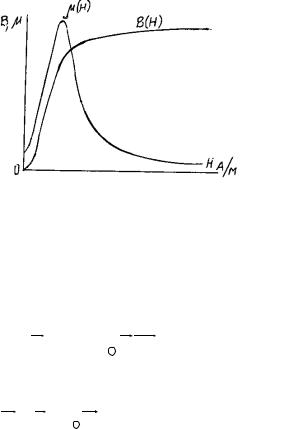
Рис. 9.2.7. Кривая намагничивания магнитопровода

Выражение (9.2.26) является законом Ома для участка магнитной цепи. Здесь

U	= Hl	м	магнитное напряжение; R		=	lм		магнитное	сопротивление
						S
м				M			м

участка магнитной цепи; lм длина участка магнитопровода, Sм – его сечение.

divB 0 BdS 0 Ф 0	(9.2.27)
S
первый закон Кирхгофа для магнитной цепи.
rot H J Hdl wI U м F	(9.2.28)

второй закон Кирхгофа (здесь F = Iw – магнитодвижущая сила МДС). Законы магнитных цепей и их параметры аналогичны законам и

параметрам электрических цепей.

		Таблица 9.2.3

Электрические цепи		Магнитные цепи
Электродвижущая сила Е		Магнитодвижущая сила F = Iw
Электрический ток I		Магнитный поток Ф
Электрическое напряжение U	l	Магнитное напряжение Uм		lм
Электрическое сопротивлениеR	l	Магнитное сопротивление R	м	lм
Электрическое сопротивлениеR	S	Магнитное сопротивление R		Sм
Закон Ома I U	S	Закон Ома Uм		Sм
Закон Ома I U		Закон Ома Uм
R		Rм
Первый закон Кирхгофа I 0		Первый закон Кирхгофа Ф 0
Второй закон Кирхгофа U E		Второй закон Кирхгофа U м F

На основе приведенной аналогии можно сделать вывод о том, что магнитные цепи могут быть рассчитаны теми же методами, что и электрические цепи.

Раздел 10. Моделирование и методы расчета статических полей и электрических параметров элементов цепи

10.1. Методы расчета и моделирование статических полей

10.1.1. Метод зеркальных отображений

10.1.1.1. Основы метода

На практике часто требуется рассчитывать ЭП зарядов, расположенных вблизи поверхностей раздела двух или нескольких сред. Трудность этих расчетов состоит в том, что на поверхностях раздела появляются наведенные заряды, закон распределения которых неизвестен. Для задач с границами раздела сред в виде плоскости, цилиндра или сферы эту трудность удается преодолеть применением метода зеркальных отображений.

В соответствии с этим методом исходная задача, в которой поле должно рассчитываться в нескольких средах, сводится к эквивалентным задачам расчета ЭП в однородной среде. Поскольку при замене сред устраняются наведенные на поверхностях раздела заряды, их действие учитывается введением фиктивных зарядов. Величина, знак и расположение фиктивных зарядов находятся из граничных условий исходной задачи.

Метод зеркальных отображений применим и для расчета МП, создаваемых токами, расположенными вблизи поверхностей раздела двух или нескольких сред.

10.1.1.2.Электрическое поле точечных зарядов, расположенных вблизи плоской поверхности раздела двух сред

Точечный заряд и плоская поверхность проводящей среды. Точечный заряд

Q расположен в диэлектрической среде с проницаемостью на расстоянии a от плоской поверхности бесконечной проводящей среды (рис. 10.1.1,а). На ней под действием заряда Q возникает заряд противоположного знака, распределенный неравномерно. Требуется определить поле в диэлектрике.

Используя метод зеркальных отображений, исходная задача приводится к эквивалентной, в которой проводящая среда заменяется диэлектриком. При этом проводящая плоскость должна быть заменена эквипотенциальной

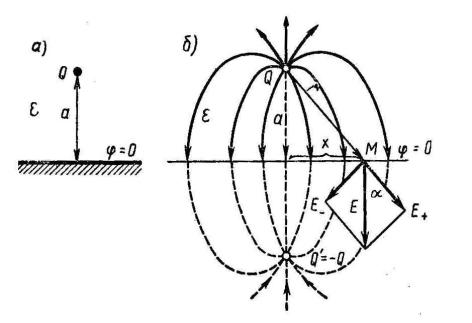
плоскостью с тем же самым значением потенциала. Ниже эквипотенциальной плоскости помещается заряд Q такой величины и в такой точке, чтобы он

вместе с заданным зарядом Q создавал в любой точке M этой плоскости один и тот же потенциал, который удобно принять равным нулю.

Для получения симметричной системы заряд Q помещается также на

Рис. 10.1.1. К расчету ЭП точечного заряда методом зеркальных отображений

откуда Q Q . Таким образом, заряд Q является как бы зеркальным отображением заряда Q .

Условия в точке расположения заряда Q и на поверхностях 0

совпадают, поэтому поля в верхних полупространствах этих задач одинаковы. Исходная задача свелась к элементарной задаче расчета поля двух разноименных одинаковых по величине зарядов, находящихся на расстоянии 2 a друг от друга в однородной среде с проницаемостью . ЭП, изображенное на рис. 10.1.1,б для исходной задачи (рис. 10.1.1,а), в верхнем полупространстве

реально, а в нижнем – фиктивно.

Для определения поверхностной плотности заряда на проводящей плоскости вычисляется напряженность поля у этой плоскости, направленная по нормали к плоскости (рис. 10.1.1,б):

E E cos E cos ,

(10.1.2)

где E	Q	E	абсолютные значения напряженности ЭП каждого из
где E	4 r 2	E	абсолютные значения напряженности ЭП каждого из
	4 r 2
зарядов.
Так как
			cos a	a	,
			cos a	a 2 x2	,
			r	a 2 x2

где x расстояние от точки M до основания перпендикуляра, опущенного из точки расположения заряда Q на плоскость, то

E 2	Q	a							Qa
										.	(10.1.3)
	4 (a2 x2 )	a2 x2					2 (a 2 x2 )1,5			.	(10.1.3)
Поверхностная плотность отрицательного заряда
	E		Qa						.		(10.1.4)
	E	2 (a	2	x	2	1,5			.		(10.1.4)
		2 (a		x		)
Сила притяжения заряда Q к							проводящей плоскости				равна силе
притяжения между зарядами Q и Q :
		F		Q 2				.			(10.1.5)
		F	16 a 2					.			(10.1.5)
			16 a 2

Полученные результаты представляют также и технический интерес. Например, электрон, вышедший из катода в вакуумной лампе на малое расстояние (порядка молекулярных размеров), при любой кривизне поверхности катода может рассматриваться как точечный заряд над проводящей плоскостью. На электрон, вышедший из катода, действует сила притяжения к зеркальному отображению, стремящаяся вернуть его на катод. При очень малых расстояниях a эта сила может быть значительной и преобладать над силой, создаваемой ЭП анода. Этим частично объясняется, почему даже при значительном анодном напряжении часть электронов возвращается на катод.

Точечный заряд и плоская поверхность раздела двух диэлектриков.

Точечный заряд Q расположен в однородном диэлектрике с проницаемостью1 на расстоянии a от плоской поверхности раздела этого диэлектрика с

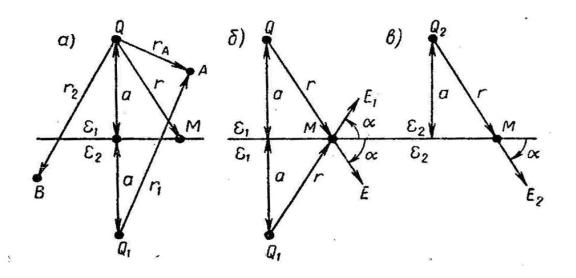
другим однородным диэлектриком, имеющим проницаемость 2 (рис.10.1.2,а). Требуется рассчитать ЭП в обеих средах.

Рис. 10.1.2. К расчету ЭП заряда на границе разных сред

В ЭП на поверхности раздела двух диэлектриков появляются связанные заряды, влияющие на ЭП в обеих средах.

Поскольку распределение этих зарядов неизвестно, рассчитать ЭП методом наложения невозможно. Так как связанный распределенный заряд обусловлен точечным зарядом Q , можно свести эту сложную задачу к простой,

заменив связанные заряды фиктивными точечными зарядами, эквивалентными по своему влиянию на поле в обеих средах.

Величина, знак и расположение фиктивных точечных зарядов определяются из граничных условий исходной задачи. В рассматриваемом случае первая простая задача (рис. 10.1.2,б) отличается от исходной тем, что диэлектрик с проницаемостью 2 заменен диэлектриком с проницаемостью 1,

а влияние исключенных при этой замене связанных зарядов учтено введением фиктивного заряда Q1 , расположенного зеркально заряду Q . Во второй простой задаче (рис. 10.1.2,в) произведена обратная замена сред, а влияние исключенных связанных зарядов учтено тем, что вместо заряда Q введен фиктивный заряд Q2 .

Так как в исходной задаче

Et1 Et2 , Dn1 Dn2 ,

(10.1.6)

то этим же условиям должны удовлетворять поля простых задач. Напряженности от зарядов Q и Q1 в некоторой точке M , лежащей у

плоскости, соответствующей поверхности раздела диэлектриков, в первой среде (рис. 10.1.2,б) равны

E	Q		, E1	Q1
						.	(10.1.7)
	4	r 2		4	r 2	.	(10.1.7)
	1			1

Следовательно, суммарная касательная составляющая в этой среде

Et1 E cos E1 cos Q Q1 cos . (10.1.8) 4 1r 2

Касательная составляющая напряженности во второй среде в той же точке

(рис. 10.1.2,в)

Et2 E2

cos

cos .

(10.1.9)

4 2 r 2

Нормальные составляющие вектора D в точке M равны

D sin D sin

Q Q1

sin ,

(10.1.10)

4 r 2

Dn2

D sin

sin .

(10.1.11)

4 r 2

На основании равенств (10.1.2) получаются два уравнения:

1 2

Q , Q

2 2

Q .

(10.1.12)

1 2

Таким образом, сложная задача сведена к двум простым. На основании теоремы единственности потенциал в верхнем полупространстве исходной задачи (рис. 10.1.2,а) совпадает с потенциалом в верхнем полупространстве первой простой задачи (рис. 10.1.2,б), поскольку эти поля имеют одинаковые граничные условия. По той же причине совпадают поля исходной и второй простых задач в нижнем полупространстве.

Следовательно, потенциал в точке А (первая среда) исходной задачи (рис. 10.1.2,а)

1	Q	Q1	=	Q	(	1	1 2	1	) ,	(10.1.13)

	4 1rA	4 1r1		4 1		rA 1 2		r1

а в точке В (вторая среда)

2	Q2	Q	.	(10.1.14)
	4 2 r2	2 ( 1 2 )r2

Легко проверить, что в точке М на поверхности раздела, где rA r1 r2 , потенциалы во всех трех задачах одинаковы:

M 1M 2M	Q		,	(10.1.15)
	2 ( 1 2 )r

что и соответствует совпадению граничных условий.
Как следует из выражений для зарядов Q1		и Q2 ,		знак заряда Q2 всегда

совпадает со знаком заряда Q , знак же заряда Q1 совпадает со знаком Q , когда1 2 , и противоположен ему, когда 1 2 . При 1 2 заряды Q1 =0, Q2 =Q , а при 2 1 заряд Q1 Q , что, в частности, соответствует случаю, когда вторая среда является проводником ( 2 ).

Электрическое поле системы заряженных тел, расположенных параллельно поверхности раздела сред. Соотношения, полученные для точечного заряда, позволяют решить и более сложные задачи. В частности, если вблизи плоской поверхности раздела двух диэлектриков расположены n точечных зарядов, то на основании принципа наложения потенциал поля равен алгебраической сумме потенциалов этих зарядов и их зеркальных отображений. При этом фиктивные заряды (изображения) определяются для каждого реального заряда такими же соотношениями, как и для уединенного точечного заряда.

Поскольку любое распределение зарядов (по объему, поверхности или линии) может быть представлено как совокупность точечных зарядов, то методом зеркальных отображений можно воспользоваться и в этих случаях.

Большое практическое значение имеет расчет полей линейных зарядов, расположенных параллельно плоским поверхностям раздела сред (линии передачи вблизи земли или стен зданий и т. д.).

Пусть бесконечно длинный провод с линейной плотностью заряда расположен параллельно плоскости раздела двух однородных диэлектриков с проницаемостями 1 и 2 на расстоянии a от этой плоскости (рис. 10.1.3).

Согласно методу зеркальных отображений фиктивные заряды (отображения) будут также линейными, а их значения и знаки определяются по формулам, аналогичным формулам для точечного заряда:

Рис. 10.1.3. К расчету ЭП длинного провода с распределенным зарядом, параллельного границе двух сред

	1		2		,		2 2		.	(10.1.16)

1		1		2		2	1	2

Затем по формуле E / 2 r					рассчитываются напряженности от 1 и 2 .
Дальнейший расчет проводится как для поля точечного заряда.

Пусть линейный заряд расположен параллельно плоским взаимноперпендикулярным поверхностям раздела между двумя диэлектриками и между ними и проводящей средой (рис. 10.1.4,а). Здесь метод зеркальных отображений применяется в два этапа. Сначала исходная задача сводится к более простой (рис.10.1.4,б) заменой проводящей среды зеркальным отображением заряда ( ) и диэлектриками 1 и 2 . Затем эта задача

аналогично тому, как это делалось для точечного и линейного зарядов, сводится к двум простейшим.

Рис. 10.1.4. К расчету ЭП линейного заряда, расположенного параллельно плоским взаимно-перпендикулярным поверхностям раздела между двумя диэлектриками и между ними и проводящей средой

10.1.1.3. Магнитное поле линейных токов, расположенных параллельно плоским поверхностям раздела сред

Бесконечно длинный провод с током I расположен параллельно плоской поверхности раздела двух однородных сред с магнитными проницаемостями 1

и 2 на расстоянии a от этой поверхности. Требуется рассчитать поле в обеих

средах.

Эта задача с помощью метода зеркальных отображений также может быть сведена к двум простым (рис. 10.1.5,б,в). При этом величину и направление фиктивных токов I1 и I2 можно получить, исходя из условий на поверхности

раздела Ht1 Ht2 и Bn1 Bn2 . Однако выражения для этих токов можно

записать и на основе подобия плоскопараллельных ЭП и МП, если в соответствии с табл. 10.1.1 в выражениях для линейных зарядов заменить на

I и	на 1/ . Тогда
	I1	1		2		I , I 2		2 1			I .	(10.1.17)
	I1	1		2		I , I 2					I .	(10.1.17)
			1		2		1			2
			1		2		1			2
Отсюда видно, что при 2					1 ток I1				имеет то же направление, что и ток
I ; при	1 2 -	обратное.				Направление				тока		I2 всегда совпадает с
направлением тока I .

Рис. 10.1 .5. К расчету ЭП бесконечно длинного провода с током I , расположенного параллельно плоской поверхности раздела двух однородных сред с магнитными проницаемостями 1 и 2

Пусть провод с током I расположен в воздушном зазоре между двумя параллельными плоскостями NN и MM , являющимися поверхностями раздела воздуха и стали (рис. 10.1.6,а). Для расчета поля в воздухе воспользуемся методом зеркальных отображений, при этом магнитную проницаемость стали можно положить равной бесконечности. Тогда влияние стали учитывается введением системы фиктивных токов, равных по величине и совпадающих по направлению с током I . Расположение этих токов подбирается из следующих соображений.

Первый фиктивный ток располагается зеркально току I относительно одной из плоскостей (например, MM ), затем реальный ток и его отображение отображаются во второй плоскости, а эти новые отображения – снова в первой плоскости и т. д. (рис. 10.1.6,б). Легко проверить, что в этом случае реальный ток и его отображения будут расположены симметрично как относительно плоскости MM , так и относительно плоскости NN . Значит, эти плоскости будут эквипотенциальными, что и соответствует граничным условиям исходной задачи.

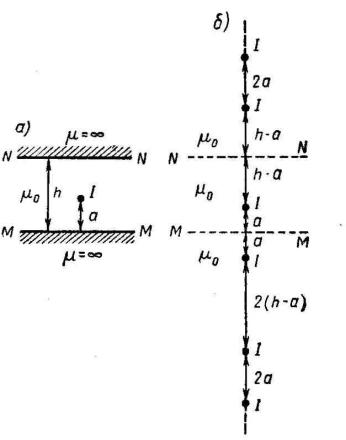
Рис. 10.1.6. К расчету МП провода с током I в воздушном зазоре между двумя параллельными плоскостями NN и MM , являющимися поверхностями раздела воздуха и стали

Теоретически таких отображений будет бесконечное множество, однако практически для дальнейшего расчета достаточно взять ограниченное их число, так как по мере удаления от воздушного зазора влияние фиктивных токов на поле в зазоре уменьшается, и это влияние легко оценить.

Затем МП в воздушном зазоре определяется как сумма МП, рассчитанных по известным формулам для однородной среды от исходного тока и его отображений.

Рассмотренные примеры имеют практическое приложение при расчетах МП в электрических машинах и других устройствах, в которых обмотки располагаются вблизи ферромагнетиков.

Следует отметить, что методом зеркальных отображений рассчитываются ЭП и МП и в тех случаях, когда поверхности раздела сред представляют собой сферы, цилиндры или совокупность плоскостей.

10.1.2.Метод разделения переменных

10.1.2.1.Общие принципы метода

Для решения линейных однородных уравнений в частных производных, каковыми в большинстве случаев являются уравнения, описывающие распределения статических ЭМП в однородных изотропных средах, часто применяется метод частных решений, восходящий в основе своей еще к Д. Бернулли и называемый иногда методом Фурье-Ламе по имени систематически разработавших его ученых.

Если такие решения могут быть найдены, то, как показывает детальное исследование, их всегда найдется бесконечное множество, причем они оказываются зависящими от одного или нескольких постоянных параметров, могущих принимать любые вещественные или комплексные значения.

Метод применяется обычно в случаях, когда поверхности, на которых заданы граничные условия, являются координатными поверхностями в ортогональных криволинейных системах координат q1, q2 , q3 .

Сущность метода состоит в том, что подлежащее интегрированию дифференциальное уравнение записывают в соответствующих координатах q1, q2 , q3 и пытаются находить частные решения этого уравнения в форме

произведения функций, зависящих каждая только от одной из переменных. Так как исходное дифференциальное уравнение линейно относительно искомой функции и ее производных, то сумма произвольного числа найденных таким способом частных решений его есть опять решение.

Получаем, таким образом, возможность составить некое весьма общее решение предложенного уравнения.

Если соответствующим выбором значений входящих в суммируемые решения параметров и постоянных можно добиться того, чтобы все решение в целом удовлетворяло всем граничным и начальным условиям и представлялось бы при этом сходящимся рядом, и если сверх того установлено, что при этих условиях предложенное уравнение имеет одно единственное решение, то найденное решение и будет правильным решением задачи.

Ниже поясним сущность метода разделенных переменных на ряде простых примеров.

10.1.2.2. Решение краевых задач на плоскости

На практике часто встречаются электроды с поверхностью цилиндрической формы. При этом форма поперечного сечения может быть произвольной. На рис. 10.1.7,а показана схема расположения электродов в электронно-оптическом устройстве; электроды здесь представляют собой пластины, перпендикулярные к плоскости чертежа, а отверстиями служат щели; на рис. 10.1.7,б изображено поперечное сечение триода, имеющего плоский катод; сетку, состоящую из длинных параллельных нитей, и плоский анод.

Практически можно получить достаточно хорошее приближение, полагая размеры электродов в направлении, перпендикулярном к плоскости (x, y) , очень большими. В таком случае во всех плоскостях, перпендикулярных к оси цилиндра, распределение потенциала и силовых линий одно и то же. В действительности, если края электродов удалены от рассматриваемой плоскости сечения, их влияние сказывается незначительно и распределение потенциала практически не зависит от координаты z . При этом трехмерное уравнение Лапласа, описывающее ЭП в триоде, сводится к двухмерному (для обозначения электрического потенциала используется здесь и в дальнейшем буква U , поскольку использована для обозначения угловой координаты):

U	2U	2U	0 ,	(10.1.18)
	x2	y2
и электрический потенциал U представляется				функцией только двух
переменных x и y .

Рис. 10.1.7. К расчету ЭП системы электродов в электронно-оптическом устройстве

Применим для решения уравнения (10.1.18) метод разделения переменных. Для этого положим, что искомый электрический потенциал можно представить как произведение двух функций, из которых каждая зависит

только от одной переменной, например для системы координат x и y :

U (x, y) X (x)Y ( y) .

(10.1.19)

Подставив это произведение в уравнение (10.1.19), получим

d 2 X

d 2Y

0 .

(10.1.20)

dx2

dy 2

Если далее обе части полученного уравнения разделить на произведение XY ,

то получим

1 d 2 X

1 d 2Y

(10.1.21)

dx2

Y dy

одна часть которого зависит только от переменной x , а другая – только от переменной y . Отсюда следует, что обе части должны быть постоянными и

иметь одно и то же значение, например k 2 . Таким образом, исходное уравнение в частных производных распадается на два обыкновенных дифференциальных уравнения второго порядка:

d 2 X	k 2 X ,	d 2Y	k 2Y .	(10.1.22)
dx2		dy 2

Решение этих уравнений известно:

X (x) Ashkx Bchkx , Y ( y) C sin ky D cos ky .

(10.1.23)

Значение так называемой постоянной разделения k может быть действительным, мнимым или комплексным, и вследствие этого характер обеих выбранных функций в действительности может быть обратным указанному. Общее уравнения Лапласа получится, если просуммировать все имеющиеся решения:

U (x, y) (Ak shkx Bk chkx)(Ck sin ky Dk cos ky) .	(10.1.24)
k

Значения всех входящих в уравнение постоянных должны быть определены из граничных условий.

Уравнение Лапласа для плоскости можно представить также в полярных координатах r, :

1	(r	U )	1	2U	0,	(10.1.25)

r r			r 2	2
		r

если полагать, что потенциал не зависит от координаты z . Это уравнение также может быть решено методом разделения переменных. Положим

U (r, ) R(r)Ф( ).

Подставив функцию (10.1.26) в уравнение Лапласа, получим

r d	( r	dR	)	1	d 2Ф	0 .

R dr		dr		Ф d 2

Аналогично предыдущему введем постоянную разделения получим

r d

) k

d 2Ф

R dr

Ф d 2

(10.1.26)

(10.1.27)

k , после чего

(10.1.28)

Решения этих двух дифференциальных уравнений уже известны: решения

первого уравнения имеют вид R r k и R r k , что можно доказать подстановкой в исходное уравнение.

Общее решение уравнения Лапласа в полярных координатах, удовлетворяющее произвольным граничным условиям, имеет вид

U (r, ) (Ak r k	Bk )(Ck sin k Dk cos k ) .	(10.1.29)
k	r k

10.1.2.3. Расчет плоскомеридианных полей

Если электроды имеют осевую симметрию, то целесообразно применять круговые цилиндрические координаты r, , z . В этом случае поле должно иметь осевую симметрию, т. е. его потенциал не зависит от угла . Уравнение Лапласа при этом значительно упрощается. Как известно, в координатах r, , z

U	1	(r	U )	1 2U	2U	0 .	(10.1.30)

	r r			r 2 2	z 2
			r

Значение потенциала не зависит от угла , если ось симметрии совпадает с осью z . При этом уравнение Лапласа для электрического потенциала приобретает вид

U )

1 U

0 .

(10.1.31)

z 2

r 2

z 2

r r

В уравнении (10.1.31) потенциал U зависит только от координат r, z , т. е.

U U (r, z) .

(10.1.32)

Уравнение (10.1.32) целесообразно решать методом разделения переменных в виде

U (r, z) R(r)Z(z) .

(10.1.33)

Подставляя U в виде (10.1.33) в уравнение (10.1.31):

Z	d 2 R		1	Z	dR	R	d 2 Z	0
	dr	2	r		dr		dz 2

Если провод с током расположен в воздухе вблизи плоской поверхности ферромагнитной среды ( 2 1 ), то для расчета МП следует ферромагнетик заменить фиктивным током (зеркальным отображением), практически равным

по величине и совпадающим			по		направлению с током			I . Например, при
2 =500 1	I1 =0,9961 I I . И деля на U RZ , получаем уравнение
		1 d 2 R		1	dR	1 d 2 Z	,	(10.1.34)

		R dr 2		rR dr		Z dz 2

левая часть которого зависит только от координаты r , а правая – только от координатыz . Равенство может выполняться только в том случае, когда обе части уравнения равны одной и той же величине, т. е.

	1 d 2 Z	k 2 и	1	d 2 R	1	dR k 2 .	(10.1.35)

	Z dz 2
			R dr2		rR dr
Итак, для определения неизвестных функций Z							и R мы получили два
обыкновенных дифференциальных уравнения. Решение первого имеет вид
		Z = Aekz Be kz .					(10.1.36)

Если k - действительное число, этому выражению целесообразно придать вид

Z Achkz Bshkz .	(10.1.37)
Если k - мнимое число, т. е. k 2 2 , где - действительное число, то
Z A cos z B sin z .	(10.1.38)

Следует добавить, что при любых значениях k общее решение может быть представлено в любой из этих трех форм. При этом, естественно, постоянные A, B при этом получаются различными.

Дифференциальные уравнения, служащие для определения функций R(r) и Z (z) , часто встречаются во многих задачах электротехники (например, в задачах экранирования). Уравнения типа R(r) исследовались впервые

Бесселем, поэтому они названы уравнениями Бесселя, а функции, служащие их решением, - функциями Бесселя. Частное решение приведенного здесь дифференциального уравнения R(r) называется функцией Бесселя нулевого

порядка и обозначается J 0 (kr) , где kr - ее аргумент. Чтобы получить полное

решение уравнения, необходимо найти еще одно решение, независимое от предыдущего. Это решение называется функцией Неймана нулевого порядка, имеет тот же аргумент kr и обозначается N0 (kr) . Отсюда общее решение дифференциального уравнения будет иметь вид

R(r) =C J 0 (kr)+ D N0 (kr) .

(10.1.39)

Если k - чисто мнимое число, т. е. k 2 2 , то J 0 (kr) = J 0 ( j r) . Эта функция вещественна.

Полное решение уравнения (10.1.39) имеет вид
U (z, r) Z (z)R(r) [Achkz Bshkz][CJ 0 (kr) DN0 (kr)].	(10.1.40)

Решение (10.1.39) содержит произвольную постоянную k . От ее выбора зависит, конечно, характер распределения потенциала. И в этом случае можно идти таким путем: придавая постоянной k произвольные значения, исследовать, какому виду эквипотенциальной поверхности соответствует полученное решение, и тем самым установить, для какой формы электродов оно применимо.

Уравнение Лапласа – линейное уравнение. Поэтому, если найдены какието два решения, их сумма также удовлетворяет исходному уравнению. Если требуется найти общее решение уравнения для поля с осевой симметрией при заданных граничных условиях, то можно искать его в виде ряда

U (z,r) [Ak chkz Bk shkz][Ck J0 (kr) Dk N0 (kr)].

(10.1.41)

Здесь k и Ak ,..., Dk определяются из граничных условий.

Значения k часто образуют ряд непрерывных, а не дискретных чисел. В таком случае решение представляется интегралом

U (z, r) [A(k)chkz B(k)shkz][C(k)J 0 (kr) D(k)N0 (kr)]dk	(10.1.42)
k
или в случае k2 2 интегралом
U (z, r) [A( )ch z B( )sh z][C( )J 0 ( j r) D( )N0 ( j r)]d .	(10.1.43)

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.2016366.65 Кб91_praktika-doc.pdf
#
16.02.20161.27 Mб1721_sbornik-kontrolnih-rabot-po-fizike.pdf
#
16.02.20161.09 Mб211_sotsiologiya-svodnyiy-fayl-2010-03-22.pdf
#
16.02.20162.53 Mб211_tekctumk.pdf
#
16.02.20162.34 Mб1951_teoriya-i-metodyi-stat-prog-ya.pdf
#
16.02.20163.12 Mб841_toe-3-2009-12-22.pdf
#
16.02.2016944.68 Кб461_umk-2-,2-chast-2010-05-13.pdf
#
16.02.20161.25 Mб101_umk-finansyi-rio-ispr-2009-11-18.pdf
#
16.02.20161.89 Mб701_umk-perehodnyie-protsessyi.pdf
#
17.08.2019547.78 Кб52 курс. 2 полугодие. Правоведение. - Основы Пра...docx
#
16.02.2016208.25 Кб92.3.rtf