
- •Федеральное агентство по образованию
- •Предисловие
- •Введение
- •Глава 1. Линейные пространства § 1. Введение
- •§ 2. Определение линейного пространства
- •I и II операции называются соответственно сложением и умножением на число и удовлетворяют следующим восьми условиям:
- •Примеры конкретных линейных пространств
- •§ 4. Линейная зависимость
- •§ 5. Базис и координаты
- •§ 6. Размерность
- •§ 7. Подпространства
- •Глава 2. Евклидовы пространства § 1. Введение
- •§ 2. Определение евклидова пространства
- •§ 3. Длина вектора
- •§ 4. Неравенство Коши-Буняковского
- •§ 5. Неравенство треугольника
- •§ 6. Угол между векторами
- •§ 7. Ортонормированный базис
- •Глава 3. Линейные операторы § 1. Определение линейного оператора
- •§ 2. Примеры линейных операторов
- •Примеры линейных операторов
- •§ 3. Действия над линейными операторами
- •Глава 4. Преобразование координат § 1. Замена базиса
- •§ 2. Ортогональные преобразования
- •§ 3. Матрица оператора при замене базиса
- •Глава 5. Несовместные системы линейных уравнений и метод наименьших квадратов § 1. Задача о проекции вектора и перпендикуляре к нему
- •§ 2. Несовместные системы линейных уравнений
- •§ 3. Метод наименьших квадратов
- •Глава 6. Собственные векторы и собственные числа § 1. Определение собственных векторов и собственных чисел
- •§ 2. Вычисление собственных векторов и собственных чисел в конечномерном пространстве
- •§ 3. Собственные векторы симметричных операторов
- •Глава 7. Квадратичные формы и их приведение к каноническому виду § 1. Приведение квадратичной формы к каноническому виду
- •§ 2. Приведение двух квадратичных форм к каноническому виду
- •§ 3. Малые колебания механических систем
- •Глава 8. Элементы теории метрических пространств § 1. Определение метрического пространства
- •§ 2. Сходимость. Полные метрические пространства
- •§ 3. Принцип сжимающих отображений
- •Библиографический список
- •191186, Санкт-Петербург, ул. Миллионная, 5
§ 5. Неравенство треугольника
Для произвольных
векторов
![]() и
и
![]() евклидового пространства выполняется
неравенство
евклидового пространства выполняется
неравенство
![]() ,
(2.7)
,
(2.7)
называемое неравенством треугольника.
Для доказательства
справедливости (2.7) заметим, что квадрат
длины вектора
![]() +
+![]() равен
скалярному произведению вектора
равен
скалярному произведению вектора
![]() +
+
![]() на самого себя, т. е.
на самого себя, т. е.
![]() .
(2.8)
.
(2.8)
Обращаясь последовательно к условию 2 в определении евклидова пространства два раза, а затем к условию 1, можем написать
![]()
![]() .
.
Используя неравенство Коши-Буняковского, получим
![]() .
(2.9)
.
(2.9)
Из сравнения (2.8)
и (2.9) следует справедливость (2.7). Заметим,
что если
![]() и
и
![]() означают векторы, изученные ранее в
курсе геометрии, то неравенство (2.7)
означает, что длина стороны треугольника
не больше суммы длин других его сторон.
означают векторы, изученные ранее в
курсе геометрии, то неравенство (2.7)
означает, что длина стороны треугольника
не больше суммы длин других его сторон.
§ 6. Угол между векторами
Вначале заметим,
что на основании неравенства
Коши-Буняковского можно утверждать,
что величина
 меньше
1.
меньше
1.
Поэтому можно ввести следующее определение.
Определение
1. Углом
между векторами
![]() и
и
![]()
![]() называют такое
число
называют такое
число
![]() (от
(от
![]() до
до![]() ),
для которого выполняется равенство
),
для которого выполняется равенство
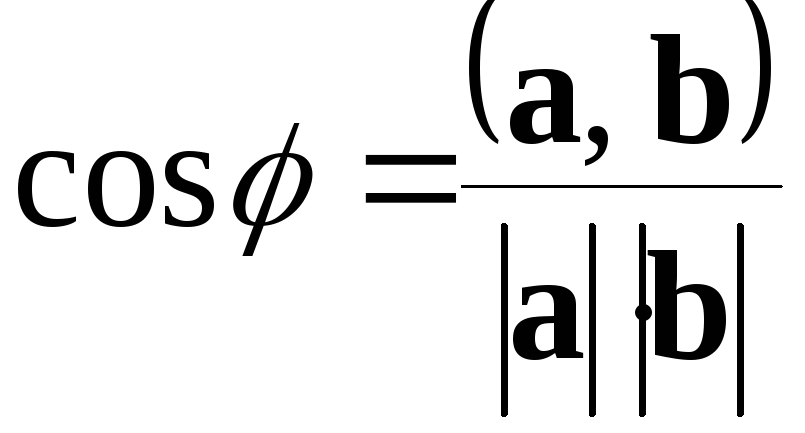 (2.10)
(2.10)
Определение
2. Векторы
![]() и
и
![]() называются ортогональными,
если выполнено равенство
называются ортогональными,
если выполнено равенство
![]() (2.11)
(2.11)
Если
![]() и
и
![]() – оба ненулевые, то это определение
означает, что угол между
– оба ненулевые, то это определение
означает, что угол между
![]() и
и
![]() равен
равен
![]() .
Нулевой вектор, по определению, считается
ортогональным любому вектору.
.
Нулевой вектор, по определению, считается
ортогональным любому вектору.
Рассмотрим примеры.
Пример 1. В
пространстве векторов, изученных ранее
в курсе геометрии, скалярное произведение
определено известным образом. Орты
![]() попарно взаимно ортогональны.
попарно взаимно ортогональны.
Пример 2. В евклидовом пространстве одностолбцовых матриц, в котором скалярное произведение определено равенством (2.3), векторы
 и
и
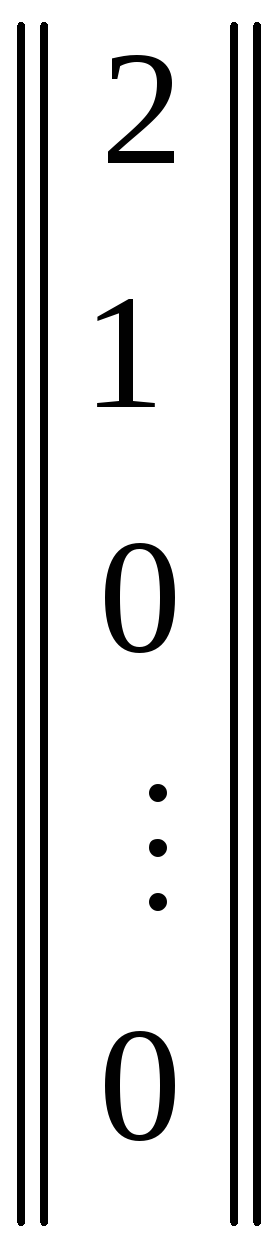
ортогональны.
§ 7. Ортонормированный базис
Определение
1. Базис
![]() евклидова
пространства
евклидова
пространства
![]() называется ортогональным, если векторы
базиса попарно ортогональны,
т. е.
называется ортогональным, если векторы
базиса попарно ортогональны,
т. е.
![]() при
при
![]() .
.
Если при этом все векторы базиса единичные, т. е.
![]() ,
, ![]() ,
,
то базис называется ортонормированным.
Теорема.
Во всяком
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() имеются ортонормированные базисы.
имеются ортонормированные базисы.
Доказательство.
Доказательство проведем для случая
![]() .
Пусть
.
Пусть
![]() – произвольный базис пространства
– произвольный базис пространства
![]() .
Докажем, что с его помощью можно построить
ортонормированный базис. Положим
.
Докажем, что с его помощью можно построить
ортонормированный базис. Положим
![]() ,
где
,
где
![]() – некоторое вещественное число,
которое мы подберем так, чтобы векторы
– некоторое вещественное число,
которое мы подберем так, чтобы векторы
![]() и
и
![]() были ортогональны, то есть
были ортогональны, то есть
![]() .
.
Используя условия 2 и 3 определения евклидова пространства, получим
![]() ,
,
откуда получим
(так как
![]() )
)
 .(2.12)
.(2.12)
Итак, если в качестве
![]() взять число, определяемое равенством
(2.12), то векторы
взять число, определяемое равенством
(2.12), то векторы
![]() и
и
![]() будут ортогональны, а так как векторы
будут ортогональны, а так как векторы
![]() и
и
![]() линейно
независимы, то из формулы, определяющей
вектор
линейно
независимы, то из формулы, определяющей
вектор
![]() ,
следует, что он не может стать нулевым.
Вектор
,
следует, что он не может стать нулевым.
Вектор
![]() определим с помощью равенства
определим с помощью равенства
![]() ,
(2.13)
,
(2.13)
где вещественные
числа
![]() и
и
![]() определим так, чтобы вектор
определим так, чтобы вектор
![]() был ортогонален к векторам
был ортогонален к векторам
![]() и
и
![]() ,
т. е. чтобы выполнялись равенства
,
т. е. чтобы выполнялись равенства
![]() ;
;
![]() .
.
Используя, как и выше, условия 2 и 3 определения евклидова пространства, можем написать
![]() ;
;
![]() ,
,
откуда, учитывая
ортогональность векторов
![]() и
и
![]() (т. е.
(т. е.
![]() ),
получим выражение для
),
получим выражение для
![]() и
и
![]()
 ,
, 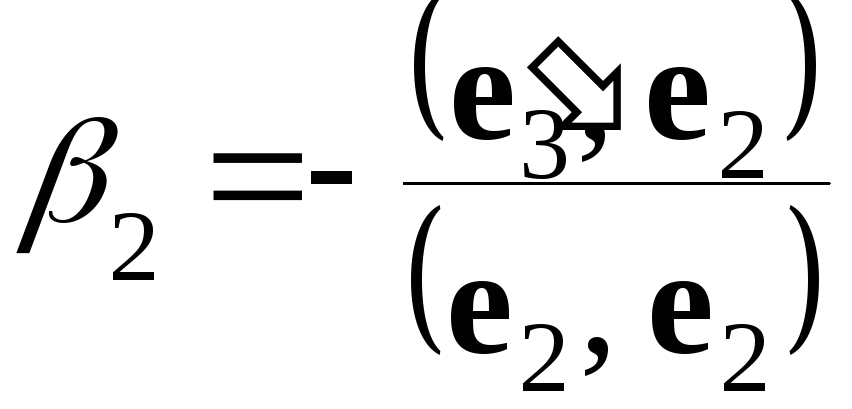 .(2.14)
.(2.14)
Итак, если в качестве
![]() и
и
![]() взять числа, определяемые равенствами
(2.14), то вектор
взять числа, определяемые равенствами
(2.14), то вектор
![]() будет ортогонален векторам
будет ортогонален векторам
![]() и
и
![]() ,
так как векторы
,
так как векторы
![]() ,
,
![]() ,
,
![]() линейно независимы, то вектор
линейно независимы, то вектор
![]() не может быть нулевым (вектор
не может быть нулевым (вектор
![]() выражается с помощью (2.13) в виде линейной
комбинации векторов
выражается с помощью (2.13) в виде линейной
комбинации векторов
![]() ,
,
![]() ,
,
![]() ).
).
Базис
![]() ,
,
![]() ,
,
![]() –
ортогональный. Но для того чтобы сделать
его ортонормированным, следует каждый
из векторов
–
ортогональный. Но для того чтобы сделать
его ортонормированным, следует каждый
из векторов
![]() ,
,
![]() ,
,
![]() поделить на его длину. Векторы
поделить на его длину. Векторы
![]() ;
; ![]() ;
; ![]()
образуют искомый ортонормированный базис.
Для случая
![]() этот
процесс следует продолжать до тех пор,
пока не найдем последний вектор.
этот
процесс следует продолжать до тех пор,
пока не найдем последний вектор.
Примененный здесь
способ получения ортонормированного
базиса из произвольного базиса носит
название процесса
ортогонализации.
Естественно, что каждый вектор
![]() в
в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() можно представить в виде
можно представить в виде
![]() ,
(2.15)
,
(2.15)
где
![]() – некоторый ортонормированный базис,
– некоторый ортонормированный базис,![]() – координаты вектора в этом базисе.
Отметим, что для координат
– координаты вектора в этом базисе.
Отметим, что для координат![]() имеют место равенства
имеют место равенства
![]() ,
, ![]() ,
,
которые получатся,
если умножить обе части равенства (2.15)
на
![]() .
.
