21.4. Градиент.

Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке

,

то этот вектор называется градиентом функции u.

При этом говорят, что в области D задано поле градиентов.

21.5. Связь градиента с производной по направлению.

Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов

.

Тогда производная по направлению некоторого вектораравняется проекции вектораgradu на вектор .

Доказательство: Рассмотрим единичный вектор и некоторую функциюu = u(x, y, z) и найдем скалярное произведение векторов 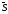иgradu.

Выражение, стоящее в правой части этого равенства является производной функции u по направлению s.

Т.е. . Если угол между векторамиgradu и обозначить через, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор единичный, т.е. его модуль равен единице, можно записать:

Выражение, стоящее в правой части этого равенства и является проекцией вектора grad u на вектор .

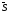Теорема доказана.

Для иллюстрации геометрического и физического смысла градиента скажем, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой- либо точке. В физике существуют такие понятия как градиент температуры, градиент давления и т.п. Т.е. направление градиента есть направление наиболее быстрого роста функции.

С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.

22.1. Основные определения.

Определение. Сумма членов бесконечной числовой последовательности называетсячисловым рядом.

При этом числа будем называть членами ряда, аu_n – общим членом ряда.

Определение. Суммы ,n = 1, 2, … называются частными (частичными) суммами ряда.

Таким образом, возможно рассматривать последовательности частичных сумм ряда S₁, S₂, …,S_n, …

Определение. Ряд называетсясходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.

Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.

22.2. Свойства рядов.

1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.

2) Рассмотрим два ряда и, где С – постоянное число.

Теорема. Если ряд сходится и его сумма равнаS, то ряд тоже сходится, и его сумма равна СS. (C  0)

3) Рассмотрим два ряда и.Суммой или разностью этих рядов будет называться ряд , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.

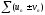Теорема. Если ряды исходятся и их суммы равны соответственноS и , то ряд тоже сходится и его сумма равнаS + .

Разность двух сходящихся рядов также будет сходящимся рядом.

Сумма сходящегося и расходящегося рядов будет расходящимся рядом.

О сумме двух расходящихся рядов общего утверждения сделать нельзя.

При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.