
- •Печатается в авторской редакции по решению Ученого совета нМетАу, протокол № 10 от 18.12.2009 г.
- •1. Принципы построения, методы анализа и синтеза линейных систем автоматического управления
- •1.1. Основные понятия и определения
- •1.2. Принципы автоматического управления
- •1.2.1. Управление по отклонению
- •1.2.2. Управление по возмущению
- •1.2.3. Комбинированное управление
- •2. Понятие передаточной функции
- •3. Частотные характеристики системы регулирования и ее элементов
- •4. Показатели качества систем автоматического управления
- •4.1. Оценка качества регулирования при стандартных воздействиях
- •4.2. Корневые критерии качества
- •4.3. Частотные оценки качества
- •5. Структурные схемы систем автоматического управления
- •5.1. Элементы структурных схем
- •5.2. Преобразование структурных схем
- •5.2.1. Последовательное соединение звеньев
- •5.2.2. Параллельное соединение звеньев
- •5.2.3. Звено, охваченное отрицательной обратной связью
- •5.2.4. Перенос звеньев
- •6. Типовые звенья систем автоматического управления
- •6.1. Апериодическое звено первого порядка
- •6.1.1. Временные характеристики звена первого порядка
- •6.1.2. Частотные характеристики звена первого порядка
- •6.2. Пропорциональное (усилительное) звено
- •6.3. Интегрирующее звено
- •6.4. Дифференцирующее звено
- •6.5. Звено чистого запаздывания
- •6.6. Звено второго порядка
- •6.6.1. Характеристики звена второго порядка
- •6.6.2. Пример звена второго порядка
- •7. Статический режим работы системы автоматического управления
- •7.1. Статическая ошибка по управлению и возмущению
- •7.2. Выбор типа регулятора
- •8. Устойчивость линейных систем автоматического управления
- •8.1. Понятие устойчивости
- •8.2. Критерий Найквиста
- •8.3. Понятие запаса устойчивости
- •8.4. Анализ устойчивости по лчх
- •9. Расчет регуляторов в системах подчиненного регулирования
- •9.1. Общие сведения
- •9.2. Настройка контура регулирования на модульный оптимум
- •9.3. Особенности настройки контуров регулирования
- •9.3.1. Интегрирующее звено в составе регулятора
- •9.3.2. Интегрирующее звено в составе объекта регулирования
- •9.3.3. Объект регулирования в виде колебательного звена
- •9.3.4. Двукратно интегрирующая система регулирования
- •10. Расчет регуляторов линейных сау по логарифмическим частотным характеристикам
- •10.1. Принципы расчета регуляторов
- •10.2. Расчет и моделирование линейных сау
- •10.2.1. Расчет параметров регулятора и моделирование переходных процессов в контуре управления положением задвижки
- •10.2.2. Расчет параметров регулятора и моделирование переходных процессов в контуре управления высотой воды в баке
- •11. Расчет и моделирование сау с запаздыванием
- •11.1. Общие сведения о ленточном дозаторе
- •11.2. Расчет и моделирование сау ленточного дозатора
- •11.2.1. Расчет параметров регулятора и моделирование переходных процессов в контуре управления положением заслонки
- •11.2.2. Расчет параметров регулятора и моделирование переходных процессов в контуре управления заполнением смесителя
- •11.2.3. Оптимизация параметров в условиях неопределенности
- •12. Разработка замкнутых систем регулирования (метод желаемой лачх)
3. Частотные характеристики системы регулирования и ее элементов
Частотные характеристики системы автоматического управления характеризуют частотный диапазон работы системы, когда изменения управляющего воздействия отслеживаются управляемой величиной. Эти характеристики можно получить при рассмотрении вынужденных колебаний на выходе системы (звена), вызванных гармоническим воздействием на входе:
|
|
(3.1) |
где
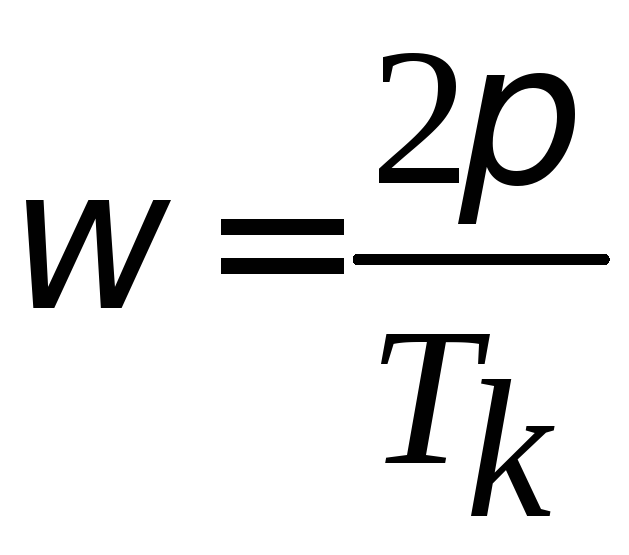 -
угловая частота входного гармонического
сигнала с периодом
-
угловая частота входного гармонического
сигнала с периодом![]() ,
,![]() - амплитуда входного гармонического
сигнала.
- амплитуда входного гармонического
сигнала.
После завершения переходного процесса на выходе линейного звена с постоянными параметрами также появляется гармонический сигнал той же частоты, но с другой амплитудой и сдвигом по фазе:
|
|
(3.2) |
где
![]() - амплитуда сигнала на выходе звена при
частоте
- амплитуда сигнала на выходе звена при
частоте![]() ,
,![]() - угол сдвига фазы выходного сигнала по
отношению к входному сигналу.
- угол сдвига фазы выходного сигнала по
отношению к входному сигналу.
Изменение
амплитуды и фазовый сдвиг являются
функциями частоты и выражают динамические
свойства системы (звена). Если изменять
частоту от
![]() до
до![]() и определять установившиеся амплитуду
и фазу выходных колебаний для разных
частот, можно получить зависимость
соотношения амплитуд
и определять установившиеся амплитуду
и фазу выходных колебаний для разных
частот, можно получить зависимость
соотношения амплитуд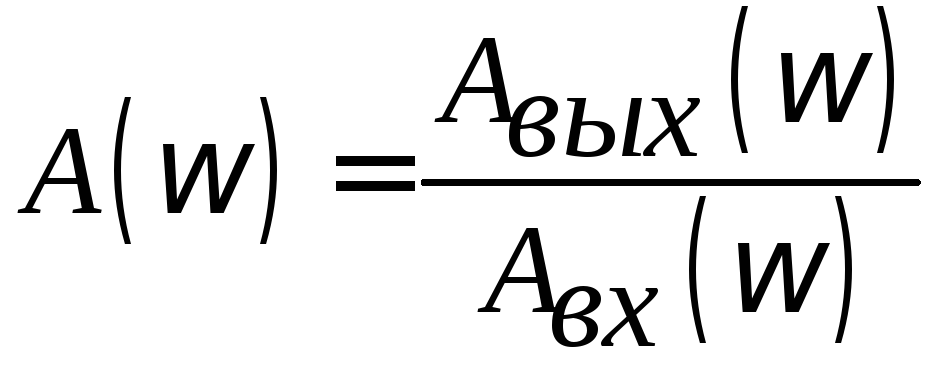 и сдвига фазы
и сдвига фазы![]() от
частоты
от
частоты
![]() .
.
![]() называют
амплитудно-частотной характеристикой
(АЧХ),
называют
амплитудно-частотной характеристикой
(АЧХ),
![]() – фазовой частотной характеристикой
(ФЧХ).
– фазовой частотной характеристикой
(ФЧХ).
Расмотрим проведение такого исследования на объекте, изображенном на рис. 3.1.
Р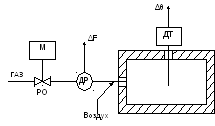 исунок
3.1
- Схема экспериментального определения
частотных характеристик нагревательной
печи
исунок
3.1
- Схема экспериментального определения
частотных характеристик нагревательной
печи
В
трубопровод подачи газа вмонтирована
дроссельная заслонка (регулирующий
орган
![]() ),
которую можно открывать и закрывать с
определенной частотой при помощи
специального механизма
),
которую можно открывать и закрывать с
определенной частотой при помощи
специального механизма![]() .
При этом формой заслонки можно обеспечить
синусоидальное изменение расхода
.
При этом формой заслонки можно обеспечить
синусоидальное изменение расхода![]() газа, измеряемого датчиком расхода
газа, измеряемого датчиком расхода![]() и
являющегося входной величиной
и
являющегося входной величиной
![]() .
Если измерять отклонение температуры
в печи
.
Если измерять отклонение температуры
в печи![]() (выходной
сигнал
(выходной
сигнал![]() )
с помощью датчика температуры
)
с помощью датчика температуры
![]() ,
то увидим, что в установившемся режиме
температура будет изменяться с той же
частотой, а максимумы и минимумы расхода
и температуры будут сдвинуты по фазе
(рис. 3.2). Амплитуда выходного сигнала
также будет изменяться при изменении
частоты.
,
то увидим, что в установившемся режиме
температура будет изменяться с той же
частотой, а максимумы и минимумы расхода
и температуры будут сдвинуты по фазе
(рис. 3.2). Амплитуда выходного сигнала
также будет изменяться при изменении
частоты.
Р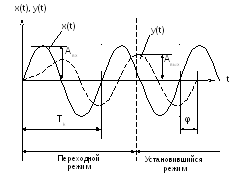 исунок
3.2
- Реакция звена (системы) на синусоидальное
воздействие
исунок
3.2
- Реакция звена (системы) на синусоидальное
воздействие
Каждой частоте входного сигнала будут соответствовать определенные амплитуда и фазовый сдвиг выходного сигнала (рис. 3.3).
Р исунок
3.3 - Установившиеся значения выходного
сигнала при различных значениях частоты
входного синусоидального сигнала
исунок
3.3 - Установившиеся значения выходного
сигнала при различных значениях частоты
входного синусоидального сигнала
Этот результат можно показать графически. Изобразив зависимость отношения амплитуд от частоты, получим АЧХ (рис. 3.4, а). Изобразив таким же образом зависимость фазового сдвига от частоты, получим ФЧХ (рис. 3.4, б).
Р исунок
3.4 - Частотные
характеристики: АЧХ (а) и ФЧХ (б)
исунок
3.4 - Частотные
характеристики: АЧХ (а) и ФЧХ (б)
На
рис. 3.5 показано построение совмещенной
амплитудно-фазовой характеристики
(АФХ). При этом на луче, выходящем из
начала координат под углом
![]() ,
откладывается
,
откладывается
![]() .
На такой характеристике частота в явном
виде отсутствует. Однако каждой точке
на кривой соответствует определенная
частота.
.
На такой характеристике частота в явном
виде отсутствует. Однако каждой точке
на кривой соответствует определенная
частота.
Р исунок
3.5 -
Амплитудно-фазовая характеристика
(АФХ)
исунок
3.5 -
Амплитудно-фазовая характеристика
(АФХ)
Запишем входной
![]() и выходной
и выходной![]() сигналы в комплексном виде и определим
частотную функцию (комплексный коэффициент
усиления).
сигналы в комплексном виде и определим
частотную функцию (комплексный коэффициент
усиления).
Комплексной
частотной функцией (комплексным
коэффициентом усиления)
![]() называется отношение комплексной
амплитуды сигнала на выходе звена к
комплексной амплитуде сигнала на его
входе, при подаче на вход синусоидального
сигнала. Это отношение определяется
после окончания переходного процесса,
вызванного подачей входного воздействия
[2].
называется отношение комплексной
амплитуды сигнала на выходе звена к
комплексной амплитуде сигнала на его
входе, при подаче на вход синусоидального
сигнала. Это отношение определяется
после окончания переходного процесса,
вызванного подачей входного воздействия
[2].
Геометрическое место конца вектора комплексного коэффициента усиления звена, при изменении частоты от нуля до бесконечности, называется частотным годографом комплексного коэффициента усиления или комплексной частотной характеристикой звена (рис. 3.5). Иногда комплексную частотную характеристику называют амплитудно-фазовой характеристикой (АФХ).
Объясним переход
от записи гармонического сигнала в
тригонометрическом виде к комплексной
форме. Изобразим на комплексной плоскости
векторы
![]() и
и
![]() ,
сдвинутые один относительно одного на
угол
,
сдвинутые один относительно одного на
угол![]() (рис. 3.6). Будем поворачивать векторы
с частотой
(рис. 3.6). Будем поворачивать векторы
с частотой![]() против часовой стрелки вокруг центра.
против часовой стрелки вокруг центра.
Р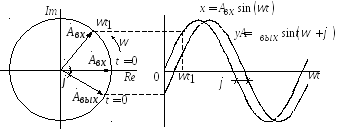 исунок
3.6 - Проекции векторов
исунок
3.6 - Проекции векторов
![]() и
и![]()
Рядом построим
график изменения проекций этих векторов
на вертикальную ось во времени
![]() .
.
Эти графики представляют зависимости:
|
|
(3.3) |
где
![]() - модуль вектора
- модуль вектора
![]() ,
,![]() -
модуль вектора
-
модуль вектора
![]() .
.
Таким образом,
существует однозначная связь гармонических
колебаний
![]() и
и![]() с векторами
с векторами![]() и
и![]() ,
расположенными на комплексной плоскости.
,
расположенными на комплексной плоскости.
Вектор
![]() при его вращении описывается уравнением:
при его вращении описывается уравнением:
|
|
(3.4) |
Вектор
![]() ,
сдвинутый на угол
,
сдвинутый на угол![]() по отношению к вектору
по отношению к вектору![]() ,
определится как:
,
определится как:
|
|
(3.5) |
Определим частотную
функцию (комплексный коэффициент
усиления)
![]() как отношение вектора выходного сигнала
как отношение вектора выходного сигнала![]() к вектору входного
сигнала
к вектору входного
сигнала ![]() :
:
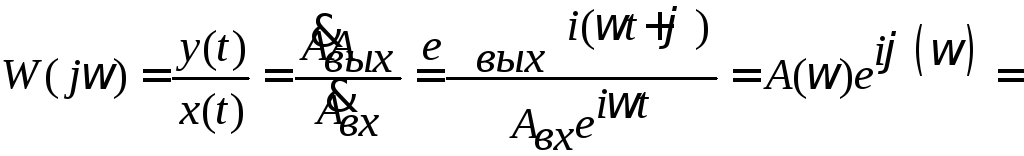
|
|
(3.6) |
где
![]() - соответственно,
модуль и фаза комплексной частотной
функции (комплексного коэффициента
усиления);
- соответственно,
модуль и фаза комплексной частотной
функции (комплексного коэффициента
усиления);
![]() -
соответственно, действительная и мнимая
части комплексной частотной функции
(комплексного коэффициента усиления).
-
соответственно, действительная и мнимая
части комплексной частотной функции
(комплексного коэффициента усиления).
Модуль
![]() и фаза
и фаза![]() частотной функции связаны с действительной
частотной функции связаны с действительной![]() и мнимой
и мнимой![]() частями следующими выражениями:
частями следующими выражениями:
|
|
(3.7) |
|
|
(3.8) |
На
комплексной плоскости (рис. 3.7) частотную
передаточную функцию определяет годограф
вектора
![]() ,
длина (модуль) которого равна
,
длина (модуль) которого равна![]() ,
а аргумент (угол, образованный этим
вектором с действительной положительной
полуосью) равен
,
а аргумент (угол, образованный этим
вектором с действительной положительной
полуосью) равен ![]() .
Кривую, которую описывает конец вектора
при изменении частоты от
.
Кривую, которую описывает конец вектора
при изменении частоты от
![]() до
до![]() ,
называют амплитудно-фазовой характеристикой
(АФХ). Таким образом, АФХ – это совмещённые
АЧХ и ФЧХ.
,
называют амплитудно-фазовой характеристикой
(АФХ). Таким образом, АФХ – это совмещённые
АЧХ и ФЧХ.

Рисунок 3.7 - Построение АФХ по частотной функции
Итак, передаточная функция полностью определяет как статические, так и динамические свойства системы (звена). Она показывает, по какому закону тот или иной сигнал, поступивший на вход, преобразуется в выходной сигнал системы или звена.
Рассмотрим получение АЧХ и ФЧХ на примере апериодического звена с передаточной функцией:
|
|
(3.9) |
Частотную функцию
(комплексный коэффициент усиления)
получим, заменив в уравнении (3.9)
![]() на
на![]() :
:
|
|
(3.10) |
Выделим из частотной
функции
![]() действительную
действительную![]() и мнимую
и мнимую![]() части:
части:
|
|
(3.11) |
|
|
(3.12) |
|
|
(3.13) |
Амплитудно-частотная
![]() характеристика:
характеристика:
|
|
(3.14) |
График АЧХ при
изменении
![]() от 0 до 100 1/с и значениях
от 0 до 100 1/с и значениях![]() ,
,![]() с,
изображен на рис. 3.8.
с,
изображен на рис. 3.8.
Р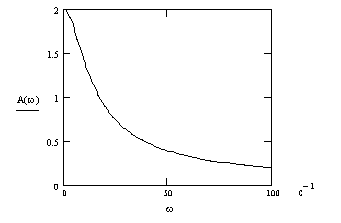 исунок
3.8 - График АЧХ
исунок
3.8 - График АЧХ
Фазовая частотная характеристика:
|
|
(3.15) |
График ФЧХ при
изменении
![]() от 0 до 100 1/с и значениях
от 0 до 100 1/с и значениях![]() ,
,![]() с,
показан на рис. 3.9.
с,
показан на рис. 3.9.
Р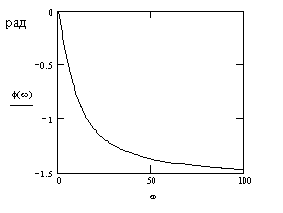 исунок
3.9 - График фазовой частотной характеристики
исунок
3.9 - График фазовой частотной характеристики
В практических расчетах амплитудную и фазовую частотные характеристики чаще всего изображают в логарифмическом масштабе, что позволяет в значительной степени упростить анализ и синтез САУ.
Коэффициент усиления в логарифмическом масштабе измеряется в децибелах. Понятие децибела введено в практику компанией Bell Telephone Labs в двадцатых годах двадцатого столетия. Сначала оно применялось для измерения логарифма отношения мощностей электрических сигналов:
|
|
(3.16) |
где
![]() ,
,![]() - мощности электрических сигналов.
- мощности электрических сигналов.
Поскольку мощность пропорциональна квадрату напряжения, то для гармонического сигнала можно записать:
|
|
(3.17) |
Поэтому в логарифмическом масштабе коэффициент усиления по напряжению, измеренный в децибелах, будет равен:
|
|
(3.18) |
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ), выраженная в децибелах, соответствующая амплитудно-частотной характеристике (3.14) определится:
|
|
(3.19) |
Фазовая частотная
характеристика
![]() ,
построенная в полулогарифмическом
масштабе (по оси ординат откладывается
угол
,
построенная в полулогарифмическом
масштабе (по оси ординат откладывается
угол![]() в градусах или радианах, по оси абсцисс
-
в градусах или радианах, по оси абсцисс
-![]() ),
называется логарифмической фазовой
частотной характеристикой (ЛФЧХ).
),
называется логарифмической фазовой
частотной характеристикой (ЛФЧХ).
В качестве единицы измерения частоты используется логарифмическая единица - декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.
В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную:
![]() .
.
ЛАЧХ и ЛФЧХ строят
обычно совместно, используя общую ось
абсцисс (ось частот). Начало координат
невозможно установить в точке
![]() ,
так как
,
так как![]() .
Поэтому начало координат располагают
в любой удобной точке в зависимости от
интересующего диапазона частот.
.
Поэтому начало координат располагают
в любой удобной точке в зависимости от
интересующего диапазона частот.
Соответствующие графики ЛАЧХ и ЛФЧХ изображены на рис. 3.10.
Р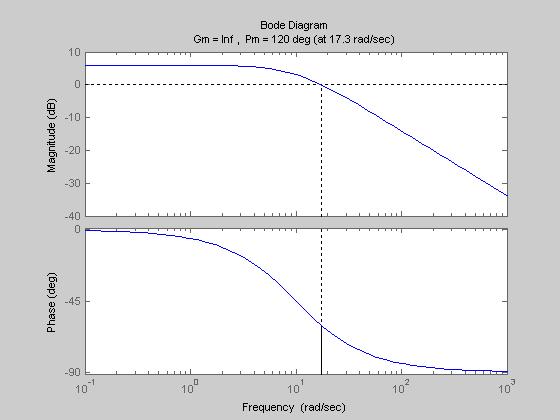 исунок
3.10 - График ЛАЧХ и ЛФЧК (диаграмма Боде)
исунок
3.10 - График ЛАЧХ и ЛФЧК (диаграмма Боде)

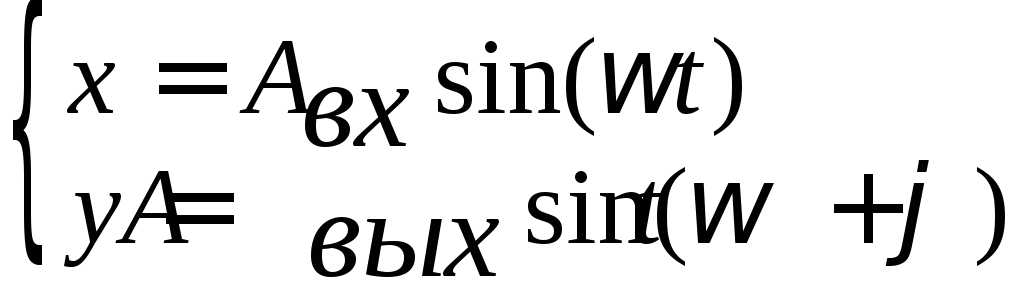 ,
,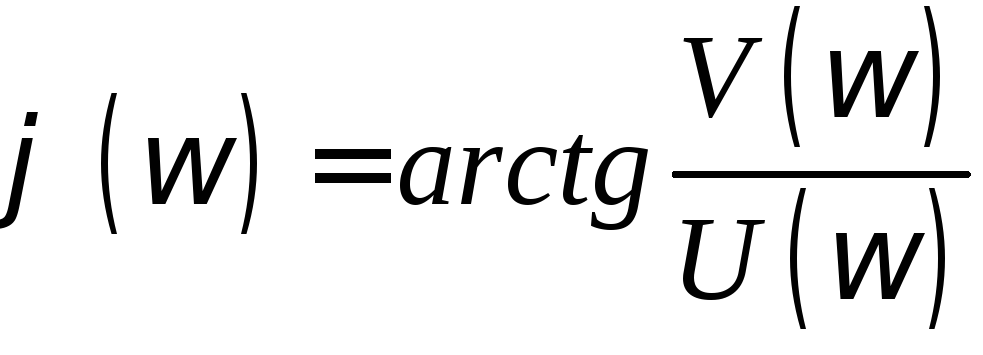 .
.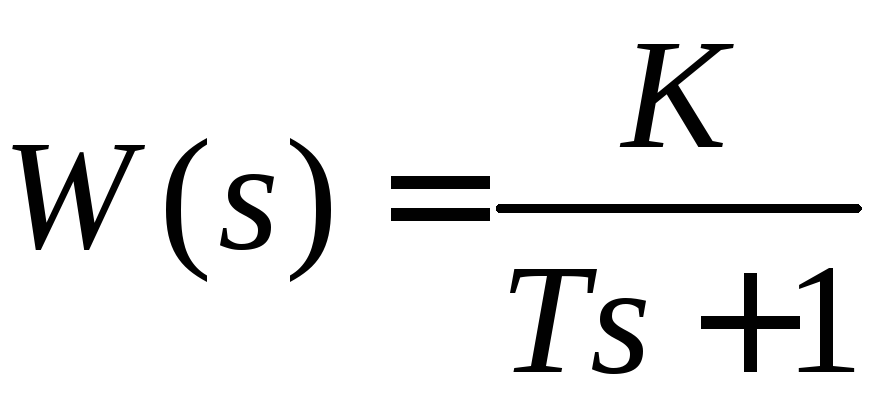 .
. .
.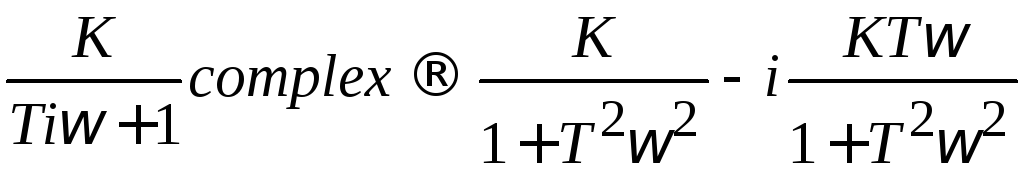 ,
, ,
,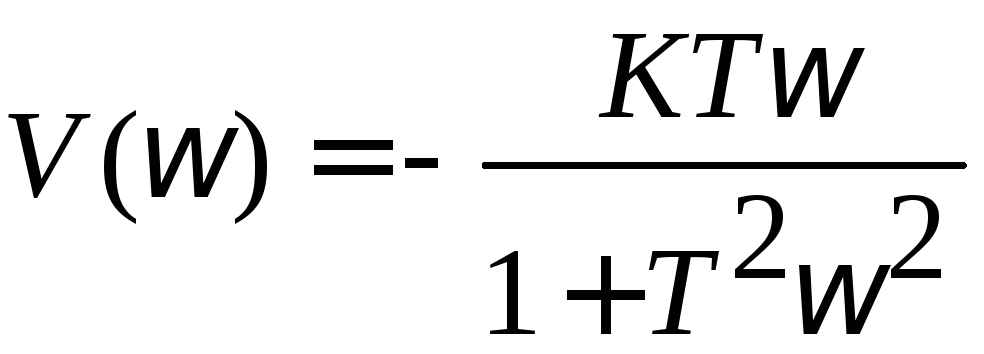 .
.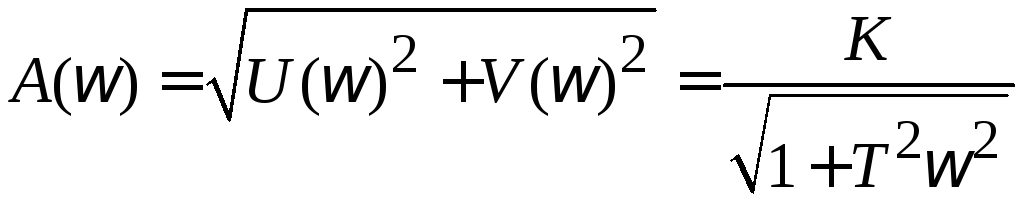 .
.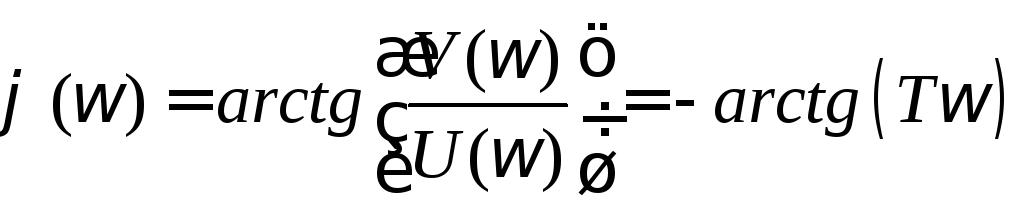 .
.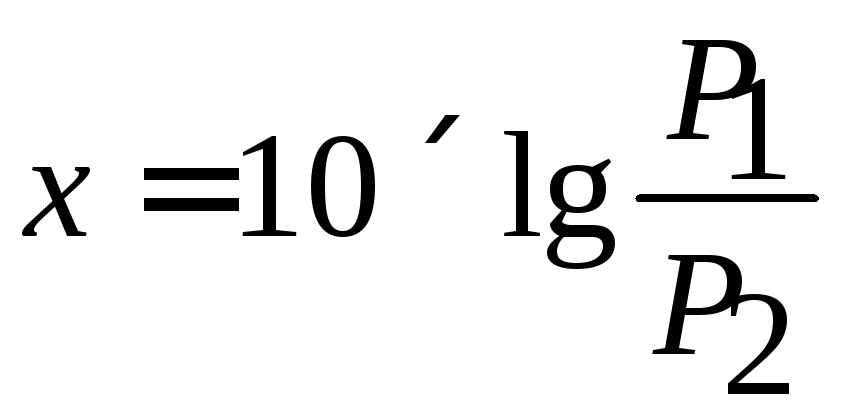 ,
дБ,
,
дБ,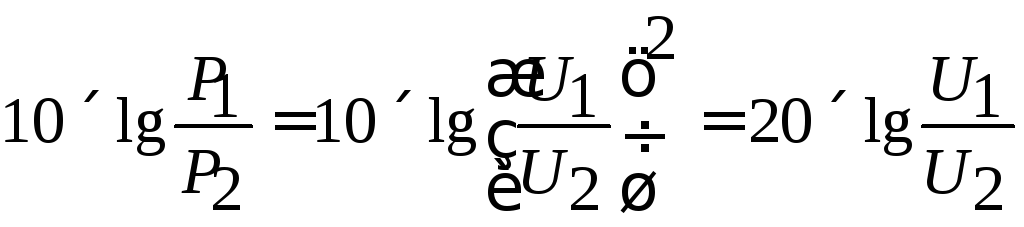 .
. .
.