МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»

Кафедра вищої геодезії

та астрономії

Лабораторна робота №6

«Прогнозування аномалій сили ваги методом колокації»

Варіант № 15

Виконав:

Студент групи ГДЗ-41

Попович О.І.

Перевірив:

Двуліт П.Д.

Львів – 2015

Мета лабораторної роботи: дати студентам навички застосування методу середньої квадратичної колокації для прогнозування значень аномалій сили ваги.

Вступ

На теперішній час розроблена низка методів, які дозволяють розв'язати задачу визначення зовнішнього гравітаційного поля Землі з тим чи іншим рівнем точності. Але, незважаючи на доволі велику кількість таких методів, метод середньої квадратичної колокації досі є основним методом визначення параметрів гравітаційного поля як в глобальному, так і в локальному масштабах.

Метод середньої квадратичної колокації вперше був запропонований в 1962 р. У. Каулою і Г. Моріцом, які застосували його для прогнозу значень сили ваги точках земної поверхні, в яких з об’єктивних причин неможливо було виконувати точні гравіметричні спостереження. При цьому був встановлений зв’язок між врівноваженням за методом найменших квадратів і прогнозом за методом колокації. Пізніше, в 1968-69 роках. Т. Краруп дав строге математичне обгрунтування цього зв’язку. Спрощений, так званий “статистичний”, підхід для загальної теорії метода колокації був розроблений Г. Моріцом в 1969-1971 роках.

Широке використання методу середньої квадратичної колокації для розв'язуван­ня задач фізичної геодезії на протязі вже майже 40 років обумовлено тим, шо цей метод дозволяє ефективно визначати невідомі величини і виконувати оцінювання іх точності за результатами вимірів, заданими у дискретній сукупності точок.

Середній квадратичний прогноз

Нехай результати вимірів після відповідного вилучення систематичної частини утворюють випадковий к - вимірний вектор

(1)

який має нульове математичне сподівання

(2)

і характеризується автоковаріаційною матрицею

(3)

Нехай т - вимірний випадковий вектор (сигнал)

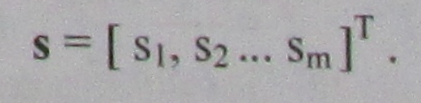(4)

мас також нульове математичне сподівання

(5)

характеризується автоковаріаційною матрицею

(6)

і зв'язаний з вектором І взаємною коваріаційною матрицею

(7)

Причому

(8)

Тоді лінійна оцінка вектора s на основі вихідних даних 1

(9)

буде мати нульове математичне сподівання (буде незміщеною):

(10)

а помилки цієї оцінки будуть характеризуватися коваріаційною матрицею

(11)

причому дисперсії помилок (діагональні елементи матриці (11)) будуть мінімальними. Отже, оцінка (9) є найкращою лінійною оцінкою вектора (4).

Формула (9) добре відома як формула середнього квадратичного прогнозу Вінера - Колмогорова.

Середня квадратична колокація

Формулу середнього квадратичного прогноза (9) можна застосувати для оцінки характеристик (наприклад, аномалій сили ваги А, висот геоїда N або відхилеь прямовисних ліній ) збурюючого потенціалу Т в деякій сукупності точок на основі його характеристик, виміряних в іншій сукупності точок. Зазначені величини зв'язані зі збурюючим потенціалом Т відомими співвідношеннями

(12)

де r,θ,λ- сферичні координати, у - нормальна сила ваги. Кожну з цих величин можна представити у вигляді лінійного функціоналуL на потенціалі Т

(13)

причому l, визначає операцію (згідно з формулами (12)), яку необхідно виконати над потенціалом T, щоби одержати ту чи іншу характеристику аномального поля. Отже, об'єднуючи в точках вимірювань ці функціонали (операції) в k - вимірний вектор

(14)

а в точках обчислень-в m- вимірний вектор

(15)

можемо записати

(16 і 17)

і знайти оцінку сигналу з (17) характеристик потенціалу Т за формулою (9).

З такої точки зору, очевидно, що в загальному формула (9) передбачає, що вектор вимірів містить в собі неоднорідні дані. Теж саме можна говорити і про вектор сигналів. Отже, важливого значення набуває проблема обчислення елементів коваріаційних матриць, які входять у вирази (9) і (11). Всі коваріації в цих виразах повинні визначатися однією й тою ж самою коваріаційною функ­цією, яка повинна залежати лише від відстані між точками, що розглядаються:

(18)

Всі необхідні коваріації виводяться за основною коваріаційною функцією за яку доцільно прийняти коваріаційну функцію збурюючого потенціалу Т:

(19)

де - поліноми Лежандра, к_п>0 - степеневі дисперсії збурюючого

потенціалу, які зв'язані з нормованими коефіцієнтами розкладу Тв ряд сферичних функцій співвідношенням

(20)

Якщо характеристики потенціалу в точках P і Qє лінійними функціоналами то

(21)

Побудова основної коваріаційної функції та обчислення на її основі коваріацій різних характеристик збурюючого потенціалу є досить складними задачами. На сьогодні відома ціла низка виразів, які апроксимують нескінчений ряд (19) при певних закономірностях зміни коефіцієнтів k_n.

Середня квадратична колокація при наявності помилок вимірів

Врахуємо тепер, що результати вимірювань обтяжені випадковими помилками. Тоді, виходячи із обговореного вище, можемо записати

(22)

де В - матриця розмірності (кхт),п -k - вимірний вектор випадкових помилок вимірів (шум), який характеризується нульовим математичним сподіванням

(23)

іавтоковаріаційною матрицеюС_nn яка в практичних ситуаціях приймається діагональною з елементами, рівними квадратам середніх квадратичних помилок вимірів:

(24)

Сигнал і шум вважаються некорельованими:

Середній квадратичний прогноз 2

(2) 2

Середня квадратична колокація 4

Прогноз аномалій сили ваги 7

(34) 7

(35) 7

а квадрат її середньої квадратичної помилки – вигляд 7

(37) 7

(46) 8

Згадаємо тепер відоме правило розповсюдження коваріацій. Якщо вектор х,

який характеризується автоковаріаційною матрицеюC_xx, зв’язаний з вектором у лінійним співвідношенням у = Ах, то автоковаріаційна матриця вектора у і взаємні коваріаційні матриці цих двох векторів можуть бути обчислені як

Середній квадратичний прогноз 2

(2) 2

Середня квадратична колокація 4

Прогноз аномалій сили ваги 7

(34) 7

(35) 7

а квадрат її середньої квадратичної помилки – вигляд 7

(37) 7

(46) 8

Де(31)

А обчислюючи авгоковаріаційну матрицю вектора І. заданого моделлю (22). і враховучи (25), приходимо до висновку

(32)

(33)

Отже, бачимо, що оцінка (30) відрізняється від оцінки (9) лише наявністю автоковаріаційної матриці шуму.

Таким чином, при наявності випадкових помилок вимірів ми можемо застосовувати формулу середнього квадратичного прогнозу, врахувавши автоковаріаційну матрицю шуму згідно формули (32). Автоковаріаційна матриця помилок оцінки (30), з огляду на (33) і (32), дається виразом (11).