3. Синтез сети междугородней связи.

3.1 Определить контур наименьшей длины, который объединяет узловые пункты телекоммуникационной сети в транспортное кольцо.

Дано: размещение пунктов (n= 10), линейно-кабельной канализации, представлено матрицей весов ребер графа, который отражает сеть. Весовые характеристики ребер отвечают расстояниям в километрах линейно- кабельных сооружений между пунктами сети. В качестве указанной матрицы используйте матрицу весов, полученную при выполнении задания 1.

Решением задачи является определение маршрута наименьшей длины. Контур, который включает каждую вершину графа G(N,V) только 1 раз, называется гамильтоновым контуром (или гамильтоновым циклом).

В каждой перестановке можно поставить в соответствие, определенное число, которое определяет длину маршрута как сумму ребер цикла, который соединяет все 10 вершин графа G(N,V). Воспользовавшись графомG(рис 1.1) определим длину каждого маршрута и выбираем наименьшую.

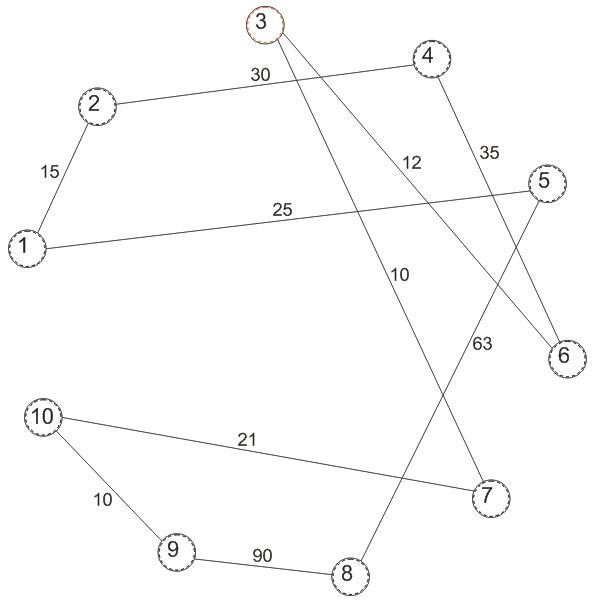
Рисунок 3.1 – график цикла наименьшей длины с первой вершины в первую.

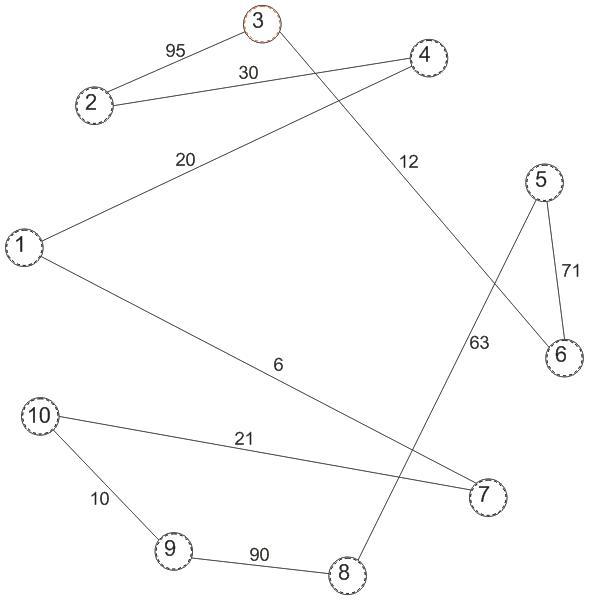
Рисунок 3.1 – график цикла с второй вершины в вторую.

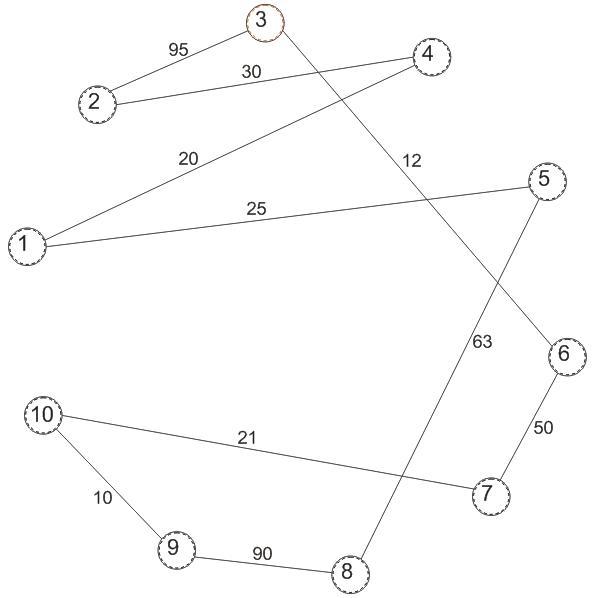
Рисунок 3.1 – график цикла с третей вершины в третью.

Рисунок 3.1 – график цикла с четвертой вершины в четвертую.

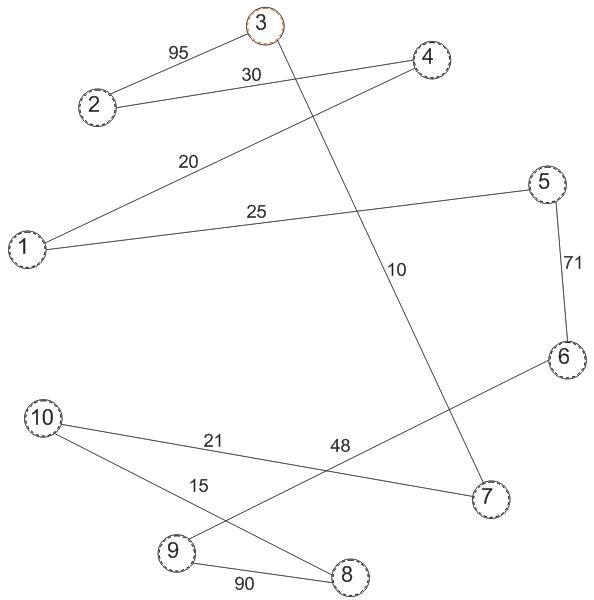
Рисунок 3.1 – график цикла с пятой вершины в пятую.

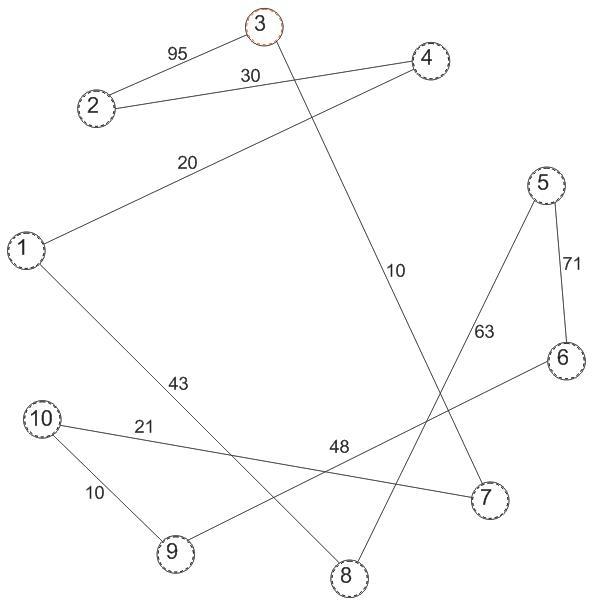
Рисунок 3.1 – график цикла с шестой вершины в шестую.

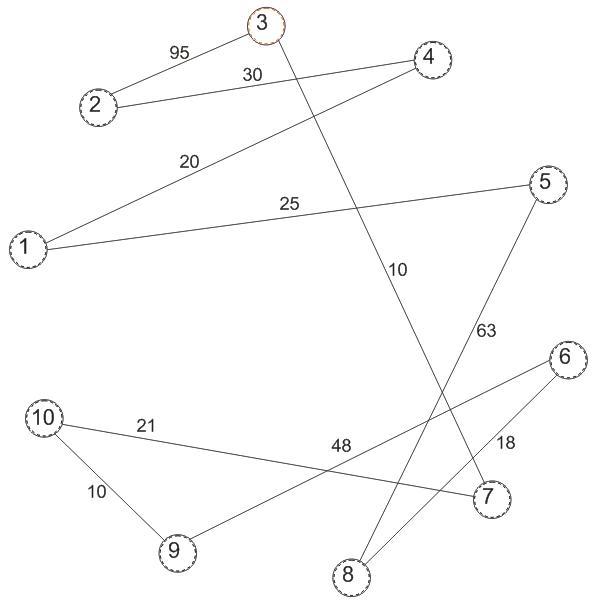
Рисунок 3.1 – график цикла с седьмой вершины в седьмую

Рисунок 3.1 – график цикла с восьмой вершины в восьмую.

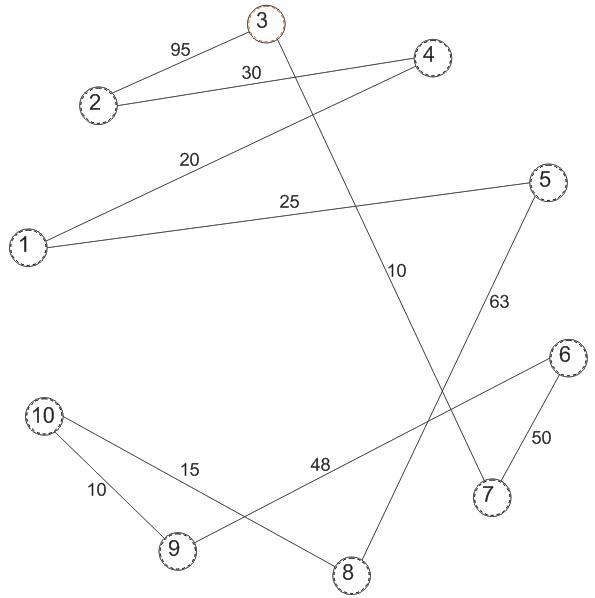
Рисунок 3.1 – график цикла с девятой вершины в девятую.

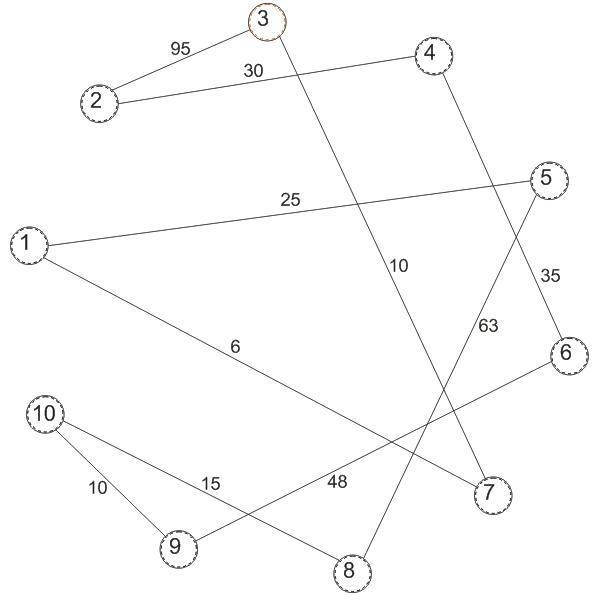
Рисунок 3.1 – график цикла десятой вершины в десятую.

3.2 Дать письменные ответы на следующие ключевые вопросы:

1. В чем заключается «задача коммивояжера»?

2. Что является точным решением «задача коммивояжера»?

3. Какой контур называется гамильтоновым циклом?

4. Что называется эвристикой? Какие алгоритмы относятся к эвристическим?

5. Сформируйте достоинства и недостатки точных и эвристических алгоритмов.

Ответы:

1. Задачей коммивояжера является поиск маршрута наименьшей длины.

2. Точным решением «задача коммивояжера» является гамильтонов цикл наименьшей

длины.

3. Контур, включающий каждую вершину графа равно один раз, называется гамильтоновым контуром (или гамильтоновым циклом).

4. Эвристика – это основанное на опыте правило, стратегия, прием или иное средство, существенно ограничивающее поиск решения сложных задач. К Эвристике относятся приближенные алгоритмы.

5. Точные алгоритмы всегда гарантируют нахождение оптимального решения. Однако точные алгоритмы, как правило, достаточно трудоемкие с вычислительной точки зрения. Эвристические алгоритмы обеспечивают быстрое получение решения с принятой для практики точностью. Такие алгоритмы строятся с использованием рациональных, с точки зрения логики человека, правил выполнения вычислений. Эвристические алгоритмы, как правило, позволяют найти решение близкое к оптимальному.

4. Построение маршрутных матриц.

4.1 Постройте маршрутные матрицы для каждого узла сети(n= 10), которые обеспечивают выбор основного направления, а также двух обходных при упорядочении соединительных трактов от рассматриваемого узла ко всем остальным узлам.

Для остального направления (пути первого выбора) необходимо использовать кратчайшие пути по расстоянию от узла S(S= 1,…..,n) в остальные пункты сети.

Для обходных (путей второго и третьего выбора) – кратчайшие по транзитам пути при максимально допустимой транзитности T₀= 2. При наличии нескольких путей одинаковой транзитности преимущество следует отдавать пути, кратчайшему по расстоянию.

Для определения путей, кратчайших по расстоянию, в качестве исходной матрицы длин линий, которые соединяют узловые пункты сети, воспользуйтесь матрицей весов, полученной при выполнении задания 1, а для определения путей минимальной транзитности смежности.

Для расчета основного напряжения воспользуемся алгоритмом Дейкстры. Особенностью этого алгоритма является тот факт, что в процессе выполнения одновременно строятся кратчайшие пути от заданной вершины Sк остальным вершинам сети. Это объясняет тем, что любая вершинаможет оказаться промежуточной в кратчайшем пути изSвt.

Работа алгоритма реализуется с помощью расстановки у вершины меток вида (L_sj,i), гдеL_sj– длина кратчайшего пути из исходной вершиныSопределенную вершинуj, аI– предыдущая вершина в этом пути.

Метки разделаются на временные и постоянные. Временные метки могут изменятся в следствии работы алгоритма, а постоянные не изменяются:

Алгоритм Дейкстры в пошаговой форме выглядит так:

Шаг 0. Для вершиныSполагаетсяL_ss= 0, а для остальных вершинL_sj= ∞. Все вершины имеют временную метку вида (L_sj,i).

Шаг 1. Среди вершин с временными метками выбираем вершинуr, для которойL_sr=min(L_sj). Метка вершиныrстановится постоянной.

Шаг 2. Если все вершины сети получили постоянные метки – конец работы алгоритма. Иначе – переход к шагу

Шаг 3. Пересчитываем вершинные метки для вершины, смежных с вершинойr, которая получила постоянную метку на шаге 1, в соответствии с выражениемL_sj=min(L_sj,L_sr+L_rj). Переход к шагу 1.

Для определения кратчайших по транзитности путей воспользуемся алгоритмом «ярусного дерева». Данный алгоритм вмещает в себя такие шаги:

Шаг 0. Создать подмножество нулевого яруса, включив в него единственный элемент – вершинуS.Используя матрицу смежности, выписать номера столбцов в ряду с номерамиS. Элементы которой равняютсяa_ij= 1. Таким образом получено подмножество вершин первого яруса, образованное вершинойS.

Шаг 1. Создать подмножество вершин следующего яруса . Для этого:

а) по очереди выбираются вершины предыдущего яруса, для каждой из которых выбирается ряд с одноименным номером в матрице смежности;

б) Для каждого ряда выписываются номера столбцов с нулевыми элементами

в) в каждом из полученных подмножеств исключается номера вершин (номера столбцов), для которых создавались подмножества на предыдущих ярусах. Все не исключенные элементы (номера столбцов) составят подмножество следующего яруса.

Шаг 2. Если номера яруса равняются (T₀+ 1) конец. Иначе – перейти к шагу 1.

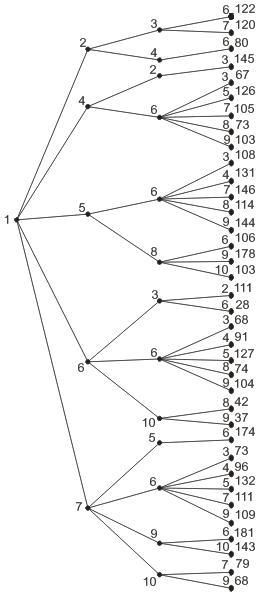
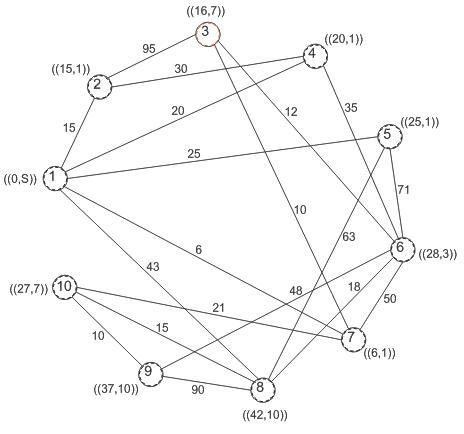
Рисунок 4.1 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел – 1)

Трассировка для узла 1:

2→1 Рисунок 4.2 - Ярусное дерево

3→7→1 (исходный узел – 1)

4→1

5→1

6→3→7→1

7→1

8→10→7→1

9→10→7→1

10→7→1

	1	2	3	4	5	6	7	8	9	10
1	-	15	-	20	25	-	6	-	-	-
2	-	50/4	16/7	45/2	106/8	55/4	-	88/5	56/8	133/8
3	-	111/7,3	67/4,6	91/7,6	126/4,6	28/7,3	79/8,10	42/7,10	37/7,10	103/5,8

Таблица 4.1- Маршрутная матрица (исходный узел – 1)

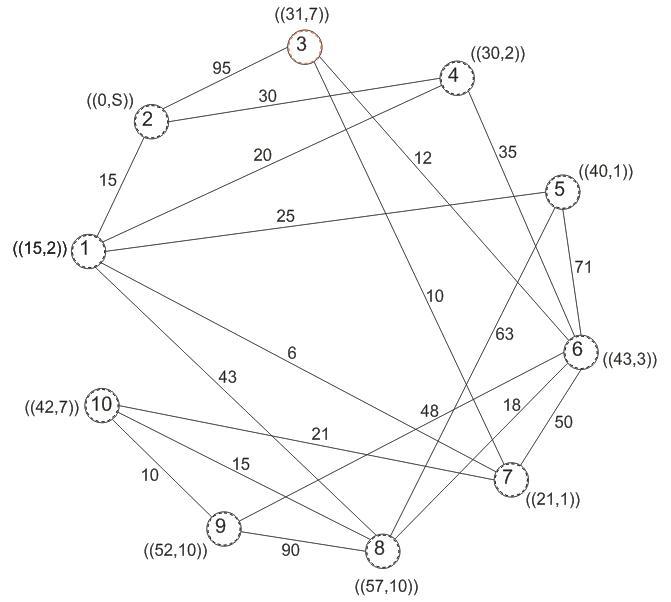
Рисунок 4.3 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел – 2)

Трассировка для узла 2:

1→2

3→7→1→2

4→2

5→1→2 Рисунок 4.4 - Ярусное дерево

6→3→7→1→2 (исходный узел – 2)

7→1→2

8→10→7→1→2

9→10→7→1→2

10→7→1→2

	1	2	3	4	5	6	7	8	9	10
1	15	-	-	-	-	-	-	-	-	-
2	50/4	-	-	35/1	40/1	65/4	21/1	58/1	-	-
3	111/3,7	-	31/1,7	143/3,6	75/4,1	70/1,4	56/4,1	83/4,6	13/4,6	42/1,7

Таблица 4.2-Маршрутная матрица (исходный узел – 2)

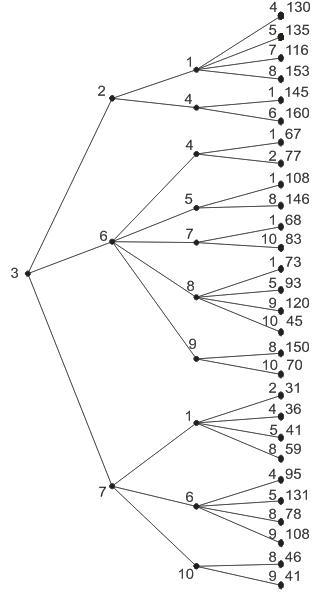
Рисунок 4.5 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел – 3)

Трассировка для узла 3:

1→7→3

2→1→7→3

4→1→7→3

5→1→7→3 Рисунок 4.6 - Ярусное дерево

6→3 (исходный узел – 3)

7→3

8→6→3

9→10→7→3

10→7→3

	1	2	3	4	5	6	7	8	9	10
1	-	-	-	-	-	12	10	-	-	-
2	16/2	-	-	47/6	83/6	60/7	62/6	30/6	60/6	31/7
3	67/6,4	31/7,1	-	36/7,1	41/7,1	160/2,4	116/2,1	46/7,10	41/7,10	45/6,8

Таблица 4.3-Маршрутная матрица (исходный узел – 3)

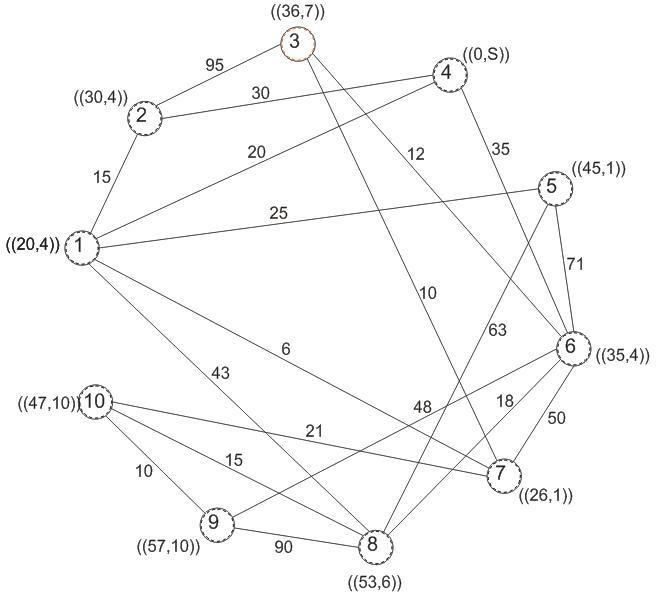
Рисунок 4.7 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –4)

Трассировка для узла 4:

1→4

2→4

3→7→1→4

5→1→4 Рисунок 4.8 - Ярусное дерево

6→4 (исходный узел –4)

7→1→4

8→6→4

9→10→7→1→4

10→7→1→4

	1	2	3	4	5	6	7	8	9	10
1	20	-	-	-	-	-	-	-	-	-
2	46/2	35/1	125/2	-	45/1	-	26/1	53/6	83/6	-
3	91/6,7	142/6,3	36/1,7	-	72/2,1	76/1,7	51/2,1	88/2,1	143/6,8	47/1,7

Таблица 4.4-Маршрутная матрица (исходный узел – 4)

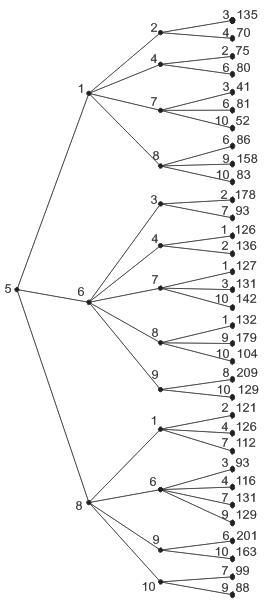
Рисунок 4.9 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –5)

Трассировка для узла 5:

1→5

2→1→5

3→7→1→5

4→1→5 Рисунок 4.10 - Ярусное дерево

6→3→7→1→5 (исходный узел –5)

7→1→5

8→5

9→10→7→1→5

10→7→1→5

	1	2	3	4	5	6	7	8	9	10
1	25	-	-	-	-	-	-	-	-	-
2	106/8	40/1	83/6	45/1	-	81/8	31/1	68/1	119/6	78/8
3	126/6,4	75/1,4	41/1,7	70/1,2	-	80/1,4	93/6,3	209/6,9	88/8,10	52/1,7

Таблица 4.5-Маршрутная матрица (исходный узел – 5)

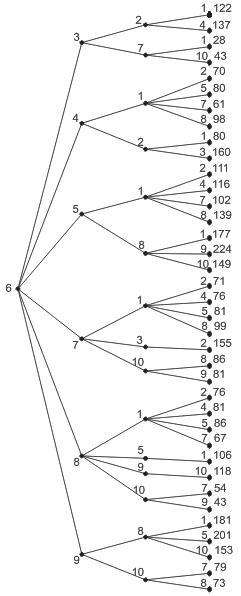
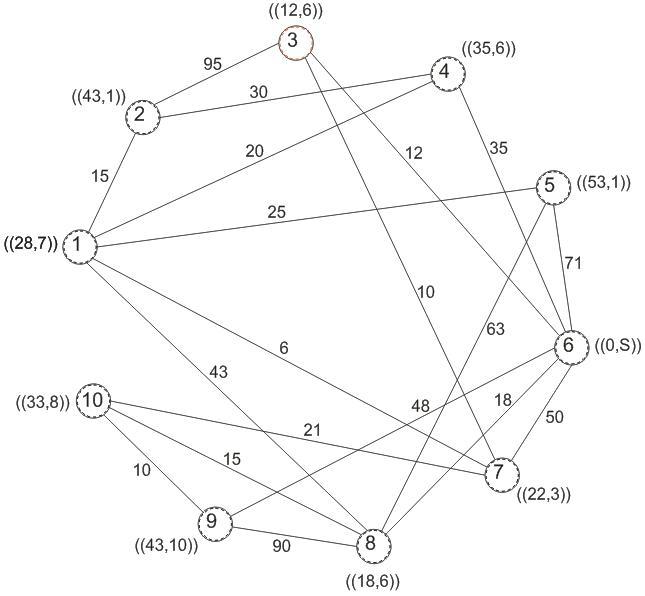
Рисунок 4.11 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –6)

Трассировка для узла 6:

1→7→3→6

2→1→7→3→6

3→6

4→6 Рисунок 4.12 - Ярусное дерево

5→1→7→3→6 (исходный узел –6)

7→3→6

8→6

9→10→8→6

10→8→6

	1	2	3	4	5	6	7	8	9	10
1	-	-	12	-	-	-	-	18	-	-
2	55/4	65/4	60/7	-	81/8	-	22/3	134/5	108/8	33/8
3	28/3,7	70/4,1	160/4,2	76/7,1	80/4,1	-	54/8,10	73/9,10	43/8,9	43/3,7

Таблица 4.6-Маршрутная матрица (исходный узел – 6)

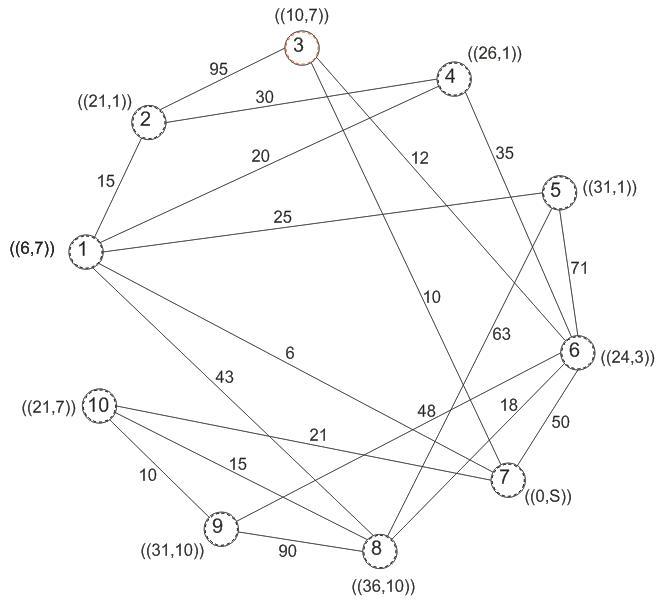
Рисунок 4.13 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –7)

Трассировка для узла 7:

1→7

2→1→7

3→7

4→1→7 Рисунок 4.14 - Ярусное дерево

5→1→7 (исходный узел –7)

6→3→7

8→10→7

9→10→7

10→7

	1	2	3	4	5	6	7	8	9	10
1	6	-	10	-	-	-	-	-	-	-
2	-	21/1	62/6	26/1	31/1	22/3	-	36/10	31/10	-
3	79/10,8	56/1,4	116/1,2	51/1,2	93/3,6	54/10,8	-	40/3,6	70/3,6	64/1,8

Таблица 4.7-Маршрутная матрица (исходный узел – 7)

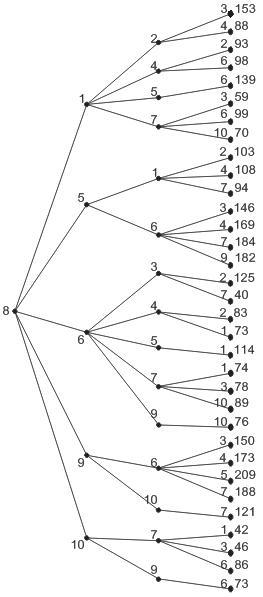
Рисунок 4.15- Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –8)

Трассировка для узла 8:

1→7→10→8

2→1→7→10→8

3→6→8

4→6→8 Рисунок 4.16- Ярусное дерево

5→8 (исходный узел –8)

6→8

7→10→8

9→10→8

10→8

	1	2	3	4	5	6	7	8	9	10
1	-	-	-	-	-	18	-	-	-	15
2	88/5	58/1	30/6	53/6	68/1	134/5	36/10	-	25/10	100/9
3	42/10,7	83/6,4	46/10,7	88/1,2	209/9,6	73/10,9	40/6,3	-	182/5,6	70/1,7

Таблица 4.8-Маршрутная матрица (исходный узел –8)

Рисунок 4.17- Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –9)

Трассировка для узла 9:

1→7→10→9

2→1→7→10→9

3→7→10→9

4→1→7→10→9 Рисунок 4.18- Ярусное дерево

5→1→7→10→9 (исходный узел –9)

6→8→10→9

7→10→9

8→10→9

10→9

	1	2	3	4	5	6	7	8	9	10
1	-	-	-	-	-	-	-	-	-	10
2	133/8	-	60/6	83/6	119/6	108/8	31/10	25/10	-	105/8
3	37/10,7	113/6,4	41/10,7	143/8,6	88/10,8	43/10,8	70/6,3	182/6,5	-	81/6,8

Таблица 4.9-Маршрутная матрица (исходный узел –9)

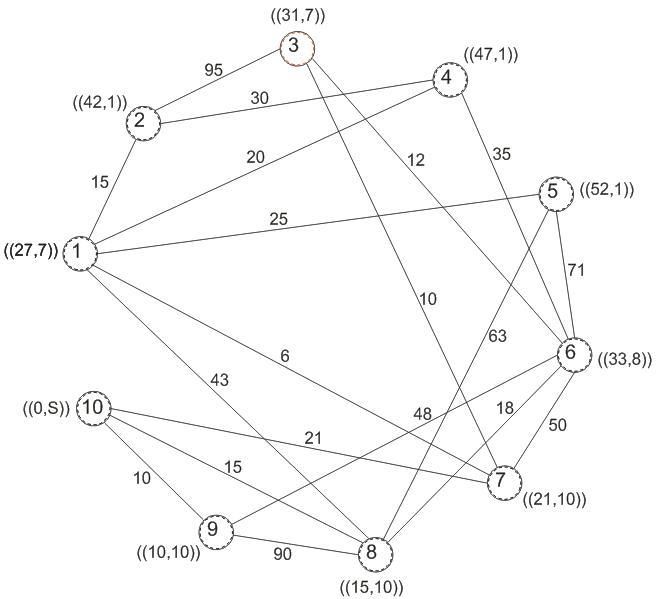
Рисунок 4.19 - Графовая модель сети построения

по алгоритму Дейкстры (исходный узел –10)

Трассировка для узла 10:

1→7→10

2→1→7→10

3→7→10

4→1→7→10 Рисунок 4.20 - Ярусное дерево

5→1→7→10 (исходный узел –10)

6→8→10

7→10

8→10

9→10

	1	2	3	4	5	6	7	8	9	10
1	-	-	-	-	-	-	-	15	10	-
2	27/7	-	31/7	-	78/8	33/8	-	100/9	105/8	-
3	103/8,5	42/7,1	45/8,6	47/7,1	52/7,1	43/7,3	64/8,1	70/7,1	81/8,6	-

Таблица 4.10-Маршрутная матрица (исходный узел –10)

4.2 Дать письменные ответы на следующие ключевые вопросы:

1. К какому классу задач относится задача построения маршрутных матриц?

2. Что называется путем в сети? Длиной пути? Транзитностью пути? Кратчайшим путем?

3. Приведите практические ситуации, в которых возникает задача определения кратчайшего пути.

4. На чем основан алгоритм Дейкстры, поиска кратчайших путей?

5. Какого вида пометки используются при работе алгоритма Дейкстры?

6. Можно ли с помощью алгоритма Дейкстры отыскать множество путей, кратчайших по транзитности? Какие исходные данные для этого потребуются?

7. Каким методом можно получить множество путей заданной транзитности?

8. В чем состоит идея метода построения ярусного дерева?

Ответы:

1. Задача построения маршрутных матриц относится к классу экстремальных.

2. Путем в сети называется последовательность вершин или последовательность дуг (ребер), соединяющих пару вершин графа. Сумма приписанных дугам (ребрам) весов в пути является длиной пути. Под транзитностью пути подразумевается количество промежуточных вершин, которые встречаются на пути между парой вершин. Путь из одной вершины в другую, имеющий минимально возможную длину, называется кратчайшим.

3. На практике кратчайшие пути определяются для создания маршрутных матриц, которые находятся на каждом узле коммутации сети.

4. Алгоритм Дейкстры основывается на том, что в процессе выполнения одновременно строятся кратчайшие пути от заданной вершины sк остальным вершинам сети. Это объясняется тем, что любая вершинаі є Nможет оказаться промежуточной в кратчайшем пути изsвt.

5. Метки разделяются на временные и постоянные. Временные метки могут изменятся вследствие работы алгоритма, а постоянные не изменяются.

6. Для определения множества путей кратчайших по транзитности при помощи алгоритма Дейкстры достаточно обладать графовой моделью сети.

7. Множество путей заданной транзитности можно получить при помощи построения так называемого «ярусного дерева».

8. Алгоритм построения «ярусного дерева» вмещает в себя такие шаги:

Шаг 0.Создать подмножество нулевого яруса, включив в него единственный элемент – вершинуs. Используя матрицу смежности, выписать номера столбцов в ряду с номеромs, элементы которой равняютсяa_sj=1. Таким образом, получено подмножество вершин первого яруса, образованное вершинойs.

Шаг 1.Создать подмножество вершин следующего яруса. Для этого:

а)по очереди выбираются вершины предыдущего яруса, для каждой из которых выбирается ряд с одноименным номером в матрице смежности;

б)для каждого ряда выписываются номера столбцов с нулевыми элементами;

в)в каждом из полученных подмножеств исключаются номера вершин (номера столбцов), для которых создавались подмножества на предыдущих ярусах. Все не исключенные элементы (номера столбцов) составят подмножество следующего яруса.

Шаг 2.Если номер яруса равняется (Т_о+1) – конец. Иначе – перейти к шагу 1.