Лабораторная работа 12

Лабораторная работа №12

Корреляционно-регрессионный анализ

Моделирование экологических и медико-биологических систем требует совместного рассмотрения нескольких их свойств и характеристик. Иногда свойства объектов проявляются независимо друг от друга, иногда между ними могут быть выявлены более или менее четкие взаимосвязи.

В естественных науках часто речь идет о функциональной зависимости (связи), когда каждому значению одной переменной соответствует вполне определенное значение другой переменной. В экологии, социологии, медицине в большинстве случаев каждому значению одной переменной соответствует множество возможных значений другой переменной.

Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону - связь является статистической. Иными словами, при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.

Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой.

Выявление корреляционных связей способствует решению широкого круга задач. В некоторых случаях требуется подтвердить не наличие, а отсутствие корреляционной связи.

Следует отметить, что наличие корреляционной связи не всегда означает наличие причинно-следственной зависимости. Существуют три пути возникновения корреляционной связи:

•Причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, признак Х - балл оценки плодородия почв, признак Y -урожайность сельскохозяйственной культуры.

•Корреляционная связь между двумя следствиями общей причины. Например, известен классический пример, приведенный крупнейшим статистиком России начала XX в. А. А. Чупровым: если в качестве признака х взять число пожарных команд в , а за признака - сумму убытков за год в городе от пожаров, то между признаками х и у в совокупности городов России существенна прямая корреляция; в среднем, чем больше пожарников в городе, тем больше и убытков от пожаров.

Данную корреляцию нельзя интерпретировать как связь причины и следствия; оба признака - следствия общей причины - размера города. Вполне логично, что в крупных городах больше пожарных частей, но больше и пожаров, и убытков от них за год, чём в мелких городах.

3

Поэтому следует помнить, что результаты корреляционного анализа необходимо проверять логикой, опираясь на теоретические и практические знания об исследуемых свойствах. Иногда при этом требуется проследить длинную цепочку взаимозависимостей. Так, в результате обработки многолетних статистических данных о случаях тяжелого производственного травматизма на угольных шахтах было установлено, что их частота определенным образом связана с фазами луны. Эта на первый взгляд весьма странная связь объясняется влиянием положения луны на приливные силы, которые проявляются не только в гидросфере, но и в литосфере, и часто играют роль «спускового крючка» для таких явлений как горный удар, выбросы газа и т.п.

Проверка гипотез о наличии линейной корреляционной связи

Основная задача корреляционного анализа состоит в выявлении связи между случайными переменными путем точечной и интервальной оценки различных (парных, множественных, частных) коэффициентов корреляции.

Для проверки гипотезы о наличии линейной корреляционной связи наибольшее распространение имеет коэффициент линейной корреляции (Пирсона),

предполагающий нормальный закон распределения наблюдений. Для двумерной нормально распределенной случайной величины XY при отсутствии линейной корреляции между X и Y коэффициент корреляции равен нулю. Поэтому процедура проверки заключается в расчете выборочной оценке коэффициента корреляции и оценке значимости его отличия т нуля.

Коэффициент корреляции – параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от –1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет. Здесь под прямой зависимостью понимают зависимость, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например, при увеличении температуры возрастает давление газа, а при уменьшении – снижается (при постоянном объеме). При обратной зависимости увеличение одного признака приводит к уменьшению второго и наоборот. Примером обратной корреляционной зависимости может служить связь между температурой воздуха на улице и количеством топлива, расходуемого на обогрев помещения.

На практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и –1. Для оценки степени взаимосвязи можно руководствоваться следующей классификацией корреляционных связей по абсолютной величине коэффициента корреляции:

-очень сильная, практически линейная зависимость между параметрами при r>0,95;

-сильная (тесная) при коэффициенте корреляции r>0,7;

-средняя при 0,50<r<0,69;

-умеренная при 0,30<r<0,49;

4

- слабая при 0,20<r<0,29; очень слабая при r<0,19. В этих случаях обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

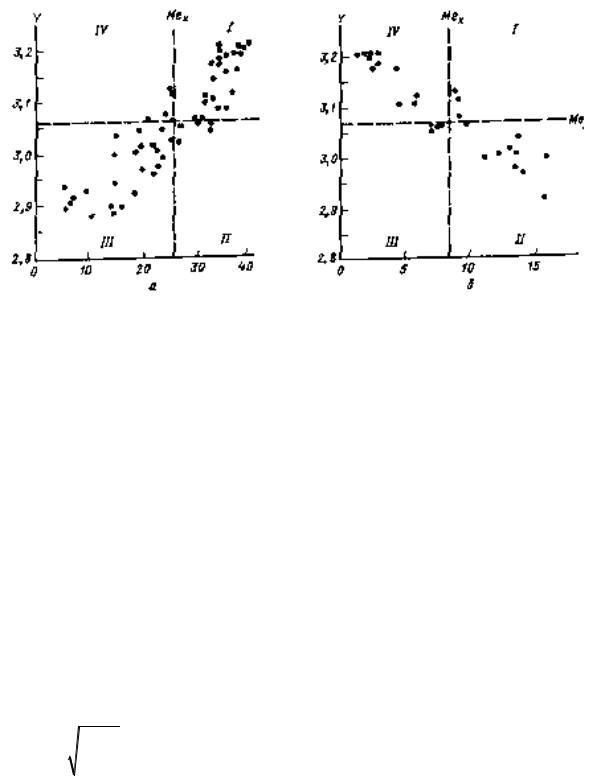
Приближенная оценка коэффициента корреляции может быть получена графическим способом с помощью корреляционного поля точек. Поле точек разделяется на четыре квадранта линиями, соответствующими медианам величин Х и Y. Для оценки коэффициента корреляции используется формула

r = (n1 −n2)(n1 +n2) , где n1 – число точек в квадрантах I, III а n2 – в квадрантах II, IV:

Рис.1. Корреляционные поля точек соотношений прямо и обратно коррелирующих величин

В Excel для вычисления выборочных парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ(массив1;массив2) или

PEARSON(массив1;массив2) где:

массив1 – это диапазон ячеек со значениями первой случайной величины - первого параметра, массив2 – это второй интервал ячеек со значениями второго параметра (измеренного у

тех же объектов, что и первый).

Также в Excel используют процедуру «Корреляция», которая позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Вычислив выборочный коэффициент корреляции, необходимо оценить его статистическую значимость. Не исключено, что ненулевое значение коэффициента является не отражением действительной связи между признаками, а получено в результате специфики данной выборки. Для того, чтобы понять, насколько значимо отличие выборочного коэффициента корреляции от 0, строят доверительный интервал (r −tσr ;r +tσr ). Средняя ошибка коэффициента корреляции вычисляется по формуле:

Напомним, что коэффициент доверия t для доверительной вероятности 0,95 равен 2,

для 0,999 – 3.

Если 0 не попадает в доверительный интервал, то коэффициент корреляции статистически значим.

Теснота линейной связи одной переменной с совокупностью других, рассматриваемой в целом, измеряется при помощи выборочного множественного (совокупного) коэффициента корреляции. Например, для трех переменных:

Этот коэффициент значим на уровне α, если

F= 2(1R(n−−R3)2 ) > Fα;2;n−3 .

ВExcel значение Fα;2;n−3 вычисляется при помощи функцииFРАСПОБР.

Вслучае, если выборочных данных недостаточно для проверки гипотезы о соответствии выборочных данных нормальным законам распределения, или если распределения существенно отличаются от нормальных, для проверки гипотезы о наличии корреляционной связи используются ранговые коэффициенты корреляции, например Спирмена или Кендалла.

Коэффициент ранговой корреляции Спирмена вычисляют по формуле

где Ri, Si – ранги сопряженных значений изучаемых величин xi и yi в выборках Х и Y; n – количество пар в выборке,

T = ∑(ti2 −1) - при суммировании по элементам выборки,

ti – длина связки, в которую входит i-й элемент выборки.

Для проверки значимости рангового коэффициента корреляции можно использовать величину

rкр = Zn(P−)1 ,

где Z(P) – значение обратной функции нормального распределения при доверительной вероятности P, рассчитывается при помощи функции НОРМСТОБР(Р).

Если расчетное значение коэффициента Спирмена (r) больше критического (rкр), то гипотеза о независимости исследуемых величин отвергается.

Пример.1. Определить наличие корреляционной связи между содержанием холестерина (Хл, TC-eng) и липопротеинов низкой плотности (ЛПНП, LDL-eng) по данным биохимических анализов пациентов приведенных в таблице 1

6

Таблица.1. Содержание Холестерина(холестерол общий TC) и Липопротеинов низкой плотности

(LDL) в биохимических анализах пациентов

Решение. Скопируем данные из таблицы на лист Excel: в столбец В – данные по содержанию Холестерина, в столбец С – по содержанию липопротеинов низкой плотностиLDL. Вычислить коэффициент корреляции Пирсона легко:

Полученное значение -0,049 показывает отсутствие линейной корреляционной связи показателей.

Для применимости коэффициента кореляции Пирсона требуется чтобы обе сравниваемые выборки были распределены нормально. По этому есть сомнения в применимости полученного результата. Следует перепроверить наличие корреляции с помощь другого клеффициента.

Вычислим коэффициент ранговой корреляции Спирмена. Сначала нужно вычислить для данных обеих выборок ранги и длины связок:

7

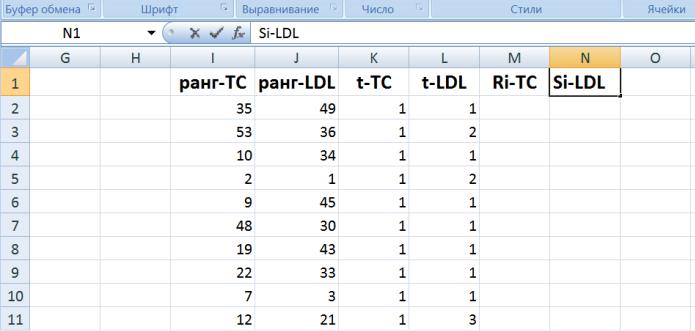
Ранги данных вычислим при помощи функции РАНГ(число;ссылка;порядок), где число – число, ранг которого вычисляется, или ячейка, в которой оно находится; ссылка – диапазон ранжируемых данных; порядок – логическое значение, равное 1 если требуется ранжирование по возрастанию. Таким образом, в ячейке I2 введем

=РАНГ(B2;B$2:B$55;1)

зафиксировав значком $ диапазон данных для дальнейшего копирования, и «растянем» результат на диапазон I2:I55.

в ячейке J2 введем

=РАНГ(C2;C$2:C$55;1)

зафиксировав значком $ диапазон данных для дальнейшего копирования, и «растянем» результат на диапазон J2:J55.

Проверим, есть ли в совмещенной выборке связки, т.е. повторяющиеся значения: вычислим для каждого данного длину связки ti, в которую оно входит при помощи функции СЧЁТЕСЛИ(диапазон;критерий), подсчитывающей в данном диапазоне данных число данных, равных данному (числовому, текстовому, логическому), указанному в переменной «критерий». В ячейке K2 введем

=СЧЁТЕСЛИ(I$2:I$55;I2)

и «растянем» результат на диапазон K2:K55, тоже выполним и для столбца L

Cтолбец L содержит неединичные значения (например, в ячейке L3), значит в соответствующей выборке есть связки. Скорректируем ранги в столбце L с учетом связок. Дело в том, что ранги, присваиваемые функцией РАНГ связанным значениям, равны первому из их порядковых номеров в ранжировке, а согласованный ранг в этом случае должен быть равен среднему арифметическому номеров. Нетрудно убедиться, что разница составляет величину (t-1)/2, где t – длина связки. Таким образом, для вычисления согласованных рангов введем в ячейке N2 формулу =J2+(L2-1)/2

и«растянем» результат:

Встолбец M можно скопировать столбец I так как в столбце K одни единицы, в общем же

случае применяется формула =I2+(K2-1)/2/. Таким образом вычисляются согласованные ранги Ri и Si.

Для применения формулы коэффициента Спирмена в случае совпадающих значений (а у нас имелись совпадения) рассчитываются величины Ri-(n+1)/2 и Si-(n+1)/2: где n =55 для наших выборок.

8

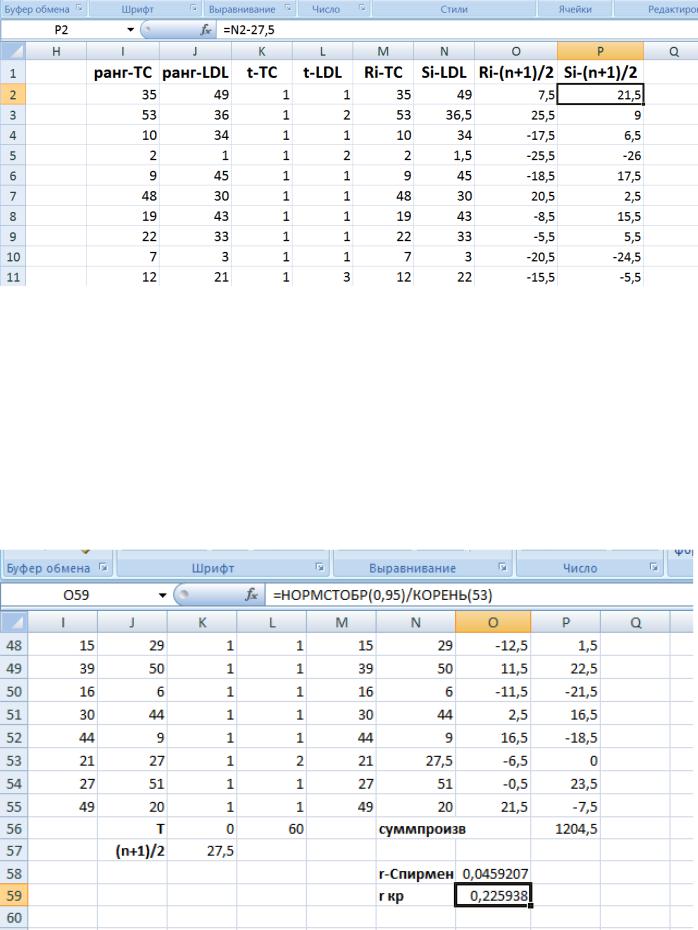
Далее, вычислим значения поправочных коэффициентов Т для обеих выборок, введя в

ячейке К56 формулу

=СУММКВ(K2:K55)-54

ископировав ее в ячейку L56.

Вячейке Р56 вычислим значение ∑(Ri −(n +1) / 2)(Si −(n +1) / 2) , введя формулу

=СУММПРОИЗВ(O2:O55;P2:P55).

Значение коэффициента корреляции Спирмена вычислим в ячейке О58, введя формулу:

=6*P56/(54^3-54-0,5*(К56+L56)).

Полученное значение коэффициента 0,046 близко к 0 и не требует проверки статистической значимости, тем не менее, определим критическое значение коэффициента Спирмена – оно равно 0,226 и превышает вычисленное значение коэффициента корреляции.

Таким образом, можно сделать вывод об отсутствии линейной корреляционной связи между содержанием Холестерина и ЛПНП в анализах.

Здесь следует подчеркнуть, что пока мы рассматривали только гипотезу о наличии линейной корреляции, когда зависимость математического ожидания одной величины от

9

значения другой выражается линейным уравнением, и поле точек соотношений величин представляет собой «облако», более или менее вытянутое около некоторой прямой. Но возможны и другие формы зависимости. Отсутствие линейной корреляции не означает отсутствия корреляционной связи вообще. Проверка гипотезы о наличии криволинейной корреляционной связи основывается на вычислении корреляционного отношения, с которым мы познакомимся позже.

Регрессионный анализ

Еще одним инструментом изучения стохастических зависимостей, наряду с корреляционным анализом, является регрессионный анализ. Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.

Влинейном регрессионном анализе связь между случайными величинами предполагается линейной. В самом простом случае в парной линейной регрессионной модели имеются две

переменные Х и Y. И требуется по n парам наблюдений (X1, Y1), (X2, Y2), ..., (Xn, Yn) построить (подобрать) прямую линию, называемую линией регрессии, которая «наилучшим образом» приближает наблюдаемые значения. Уравнение этой линии y=аx+b является регрессионным уравнением. С помощью регрессионного уравнения можно предсказать ожидаемое значение зависимой величины y, соответствующее заданному значению независимой переменной x

Вслучае, когда рассматривается зависимость между одной зависимой переменной Y и несколькими независимыми X1, X2, ..., Xm, говорят о множественной линейной регрессии.

Вэтом случае регрессионное уравнение имеет вид

y = a0+a1x1+a2x2+…+amxm,

где a0, a1, a2, …, am – требующие определения коэффициенты регрессии.

Коэффициенты уравнения регрессии определяются при помощи метода наименьших квадратов, добиваясь минимально возможной суммы квадратов расхождений реальных значений переменной Y и вычисленных по регрессионному уравнению. Таким образом, например, уравнение линейной регрессии может быть построено даже в том случае, когда линейная корреляционная связь отсутствует.

Мерой эффективности регрессионной модели является коэффициент детерминации R2 (R-квадрат). Коэффициент детерминации может принимать значения между 0 и 1 определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксимирует) исходные данные. Исследуется также значимость регрессионной модели с помощью F-критерия (Фишера) и достоверность отличия коэффициентов a0, a1, a2, …, am от нуля проверяется с помощью критерия Стьюдента.

В Excel экспериментальные данные аппроксимируются линейным уравнением до 16 порядка:

y = a0+a1x1+a2x2+…+a16x16

10

Для получения коэффициентов линейной регрессии может быть использована процедура «Регрессия» из пакета анализа. Также полную информацию об уравнении линейной регрессии дает функция ЛИНЕЙН. Кроме того, могут быть использованы функции НАКЛОН и ОТРЕЗОК для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ и ПРЕДСКАЗ для получения предсказанных значений Y в требуемых точках (для парной регрессии).

Рассмотрим подробно применение функции ЛИНЕЙН(известные_y, [известные_x], [константа], [статистика]):

известные_у – диапазон известных значений зависимого параметра Y. В парном регрессионном анализе может иметь любую форму; в множественном должен быть строкой либо столбцом; известные_х – диапазон известных значений одного или нескольких независимых

параметров. Должен иметь ту же форму, что и диапазон Y (для нескольких параметров – соответственно несколько столбцов или строк); константа – логический аргумент. Если исходя из практического смысла задачи

регрессионного анализа необходимо, чтобы линия регрессии проходила через начало координат, то есть свободный коэффициент был равен 0, значение этого аргумента следует положить равным 0 (или «ложь»). Если значение положено 1 (или «истина») или опущено, то свободный коэффициент вычисляется обычным образом; статистика – логический аргумент. Если значение положено 1 (или «истина»), то

дополнительно возвращается регрессионная статистика (см таблицу 5.2), используемая для оценки эффективности и значимости модели.

В общем случае для парной регрессии y=аx+b результат применения функции ЛИНЕЙН имеет вид:

Табл.5.2.Выводной диапазон функции ЛИНЕЙН для парного регрессионного анализа

В случае множественного регрессионного анализа для уравнения y=a0+a1x1+a2x2+…+amxm в первой строке выводятся коэффициенты am,…,a1,а0, во второй – стандартные ошибки для этих коэффициентов. В 3-5 строках за исключением первых двух столбцов, заполненных регрессионной статистикой, будет получено значение #Н/Д.

Вводить функцию ЛИНЕЙН следует как формулу массива, выделив вначале массив нужного размера для результата (m+1 столбец и 5 строк, если требуется регрессионная статистика) и завершив ввод формулы нажатием CTRL+SHIFT+ENTER.

Оценка значимости полученной регрессионной модели проводится следующим образом:

•F-статистика используется для того, чтобы определить, является ли наблюдаемая связь зависимой и независимых переменных случайной. Критическое значение F-критерия рассчитывается при помощи функции FРАСПОБР(α;k1;k2), где k2-полученное число степеней свободы, k1=n-1-k2. Если значение F-статистики выше критического, то регрессионная модель в целом значима.

11

Можно также определить вероятность случайного получения высокого значения F- статистики при помощи функции FРАСП(F;k1;k2)

• T-статистика позволяет оценить значимость каждого полученного коэффициента наклона. Для этого следует разделить коэф.наклона на станд.ошибку и сравнить полученное значение t-статистики с критическим, найденным по формуле СТЬЮДРАСПОБР(α;k2). Если значение t-статистики меньше критического, то соответствующий коэффициент может считаться нулевым, а это означает, что влияние соответствующей независимой переменной на зависимую переменную недостоверно, и эта независимая переменная может быть исключена из уравнения.

Функцию ЛИНЕЙН можно использовать также для аппроксимации по методу наименьших квадратов с помощью других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Так, для получения парной квадратичной регрессионной модели следует вычислить квадраты значений аргумента Х и построить линейную регрессионную модель с аргументами Х и Х 2. Однако надо помнить, что чем выше степень полиномиального регрессионного уравнения, тем выше его точность (коэффициент детерминации) и тем меньше значимость при небольшом объеме выборки. Необходимо иметь хотя бы 5-6 известных пар данных на каждый определяемый коэффициент уравнения регрессии.

Для вычисления коэффициентов экспоненциальной регрессии в Excel существует функция ЛГРФПРИБЛ. Функция РОСТ для экспоненциальной регрессии позволяет получить значения Y в требуемых точках и имеет тот же смысл, что и функция ПРЕДСКАЗ для линейной регрессии.

Если полученное уравнение регрессии оказалось значимо, его используют для прогнозирования значения зависимого признака Y при конкретных значениях независимых признаков Xi.Прогноз будет тем точнее, чем выше коэффициент детерминации.

Кроме того, уравнение парной линейной регрессии (даже незначимое) используется для определения корреляционного отношения, характеризующего тесноту криволинейной корреляционной связи, если доказано отсутствие линейной корреляции:

где yx – «выровненные» значения y, вычисленные по уравнению линейной регрессии, σy2 - дисперсия выборки Y (вычисляется в Excel при помощи функции ДИСПР).

Статистическая значимость отличия корреляционного отношения от нуля проверяется с помощью критерия

При равенстве истинного корреляционного отношения нулю величина θy распределена

нормально с математическим ожиданием 0 и дисперсией 1, что позволяет определять критические значения θy для заданных доверительных вероятностей по таблицам

нормального распределения. Если расчетное значение θy превышает критическое, гипотеза об отсутствии корреляционной связи отвергается.

12