Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка 1807

.pdf

Скачиваний:

Добавлен:

07.02.2016

Размер:

276.95 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

ЗАВДАННЯ 3.

Визначити дисконтований прибуток за 3 роки при процентній ставці 8%, якщо базові капіталовкладення склали 10 млн. гривень, а очікуване щорічне зростання капіталу 1 млн. гривень.

Розв’язок

Визначення початкової суми по її кінцевій величині, отриманій за T років при річному проценті P , називається дисконтуванням. Нехай прибуток за рік змінюється за часом і описується функцією f (t) при питомій нормі процента, що дорівнює і, процент

обчислюється поперервно. Тоді дисконтований прибуток K за час T обчислюється за формулою:

K = ∫ f (t)e− it dt

У нашому випадку очевидно, що капіталовкладення задається функцією

f (t) = 10 + 1t = 10 + t ;

i =

= 0.08

100

Тоді

100

u = 10 + t; du = dt

K = ∫ (10 + t)e − 0.08 t dt =

dv = e

− 0.08 t

; v =

e − 0.08

− 0.08

= − 12 .5 e − 0.08 t (10 + t )

+ 12 .5 ∫ e − 0.08 t dt =

=125 − 13 12.5 e − 0.24 − 156 .25 e− 0.08 t

=125 − 162.5 e −0.24 − 156.25 e −0.24 + 156.25 =

=281.25 − 318.5 e−0.24 ≈ 30.5 млн. гривень.

Це означає, що для отримання однаково нарощеної суми через три роки щорічні вклади від 10 до 13 млн. гривень рівноважні одночасному початковому вкладу 30.5 млн. гривень при тій самій неперервній процентній ставці.

ЗАВДАННЯ 4.

Знайти середнє значення часу, який затрачений для освоєння випуску одного виробу в період освоєння від 10 до 20 виробів, якщо затрата часу на 1-й виріб a = 200 хв., показник виробничого процесу

b = 0.5

Розв’язок

Нехай відома функція t(x), що задає зміну затрат t на

виготовлення продукції в залежності від ступеня освоєння виробництва, де x - порядковий номер виробу в партії товару. Тоді

середній час tсеред , затрачений на виготовлення одного виробу в

період освоєння від „α ” до „β” виробів, обчислюється за теоремою про середнє значення визначеного інтегралу:

tсеред

α∫

t(x)dx

β − α

Що стосується функції зміну затрат часу

t(x), то як правило,

вона така:

t = a x−b ,

де

a - затрата часу на один виріб,

b - показник виробничого процесу.

У нашому випадку

) =

−

0 . 5 ,

t ( x

200 x

x1/ 2

tсеред =

∫

200x−0.5dx =

200

∫

x− 0.5dx = 20

− 10

1/ 2

= 40

−

10) ≈ 52.3 хв.

= 40( 20

ЗАВДАННЯ 5.

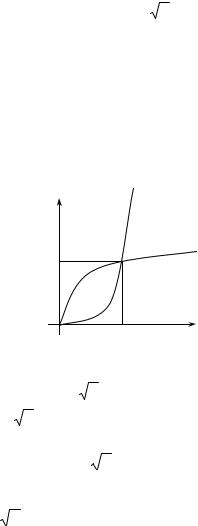
Знайти площу фігури, обмеженої заданими лініями:

	y = x2 , y = x .
Розв’язок		обмеженої лініями y = f1(x) ,
Площа	криволінійної трапеції,
y = f2 (x) ,	x [a,b], такими що	f2 (x) ≥ f1(x) , обчислюється за

формулою:

S = ∫( f2 (x) − f1(x))dx

Побудуємо фігуру:

Знайдемо координати точок перетину парабол:

= x

x1 = 0, x2

= 1

x = x

= x

= 0, y

= 1

На відрізку [0, 1]

x ≥ x2 ,

тоді:

3 / 2

S =

∫

( x − x

2 )dx =

−

кв. од.

3/ 2

0 3 3 3

ЗАВДАННЯ 6.

а) Диференціальне рівняння першого порядку вигляду

N (x)dx + M ( y)dy = 0

називають рівнянням з відокремленими змінними.

Приклад 13	2x+ y + 3x−2 y y′ = 0 .
Розв’язати рівняння

Для визначення типу заданого диференціального рівняння першого порядку запишемо його у такому вигляді

3x	dy	= −2x 2 y	3x	dy + 2x 2 y dx = 0 .
32 y			32 y
	dx

Приведемо рівняння до рівняння з відокремленими змінними шляхом його ділення на 3x 2 y . Одержимо:

2 x

dx = 0

dx = 0 .

32 y 2 y

(9 2) y

Шляхом інтегрування одержимо

− y

2 x

18− y

2 x

∫18

dy + ∫

dx = C −

: ln

= C .

ln18

Отже, загальним інтегралом заданого рівняння буде

−

= C .

18y

ln18

б)	Однорідним	диференціальним			рівнянням	першого
порядку називають рівняння, яке можна звести до вигляду
		y′ = f (x, y) ,
де функція	f (x, y) не змінюється при заміні				x та y на	tx та ty ,
тобто задовольняє умові		f (tx,ty) = f (x, y) .
		f (tx,ty) = f (x, y) .
Приклад 14
Розв’язати рівняння		y′ =	y
				.
				.
			x + y

Це рівняння є одноріднім тому, що для правої частини рівняння виконується умова:

	ty	=
	tx + ty	=
	tx + ty

При підстановці u = y x

t (x + y)

маємо:

x+ y

y = u x y′ = u′ x + u .

Тому задане рівняння прийме вигляд

u′ x + u =

u x

u′ x =

− u

+ u x

+ u

u − u − u2

= −

1+ u

du = −

1+ u

Останнє рівняння є рівнянням з відокремленими змінними. Інтегруючи його, знаходимо:

∫1

du= −

−lnu = lnx+ lnC

= ln(Cux)

∫ x

Підставимо замість u значення y та одержимо загальний x

розв’язок

x = ln Cy x = ln(Cy) y .

в) Лінійним диференціальним рівнянням першого порядку називають рівняння, яке містить шукану функцію y та її похідну y′ у першому степеню. Таке рівняння можна привести до вигляду

y′ + P(x) y = Q(x) .

Приклад 15			1) y′ + y = x − 1 .
Розв’язати рівняння	(x2	−	1) y′ + y = x − 1 .
Запишемо це рівняння у вигляді
y′ +	y		=	x − 1 .
	x2 − 1			x2 − 1

Це рівняння є лінійне диференціальне рівняння першого порядку, його розв’язок будемо шукати у вигляді

y = u(x) v(x) .

(1)

Одну із цих функцій можна взяти довільно, а друга буде визначатися так, щоб їх добуток задовольняв рівняння.

Запишемо
	y′ = u′(x) v(x) + u(x) v′(x)						(2)
Підставимо (1), (2) у задане рівняння. Тоді
	1					x − 1
	u′ v + u v′ + x2 − 1 u v =				x2 − 1
або	u′ v + u (v′ +		1	v) =		x − 1 .	(3)
		x2 − 1				x2 − 1
	Визначимо v так, щоб вираз у дужках дорівнював нулю,
тобто виконувалась рівність
	1		v = 0 .
	v′ +
	v′ +	x2 − 1

Це рівняння першого порядку з відокремлюваними змінними. Відокремлюючи змінні, одержимо

= −

∫

= −∫

x2 −1

x + 1

v (x) =

x − 1

Підставимо функцію v у рівняння (3). Одержимо
x	+ 1 12			x − 1		x − 1	x − 1
u′			=	x2 − 1	du =				dx

x	− 1					x2 − 1 x + 1
		dx			−3		2
u = ∫				= ∫(x + 1) 2 d(x + 1) = −				+ C .
		3					x + 1
	(x + 1)		2

Підставимо одержані функції u , v та отримаємо загальний розв’язок

y =	x + 1	−	2		= −	2	+ C	x + 1
y =		−		+ C	= −		+ C	.
	x − 1		x + 1			x − 1		x − 1
	x − 1		x + 1			x − 1		x − 1

ЗАВДАННЯ 7.

Лінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами має вигляд

a0 y′′ + a1 y′ + a2 y = 0 .

Складемо до нього характеристичне рівняння:

a0 k 2 + a1k + a2 = 0 .

При знаходженні коренів характеристичного рівняння можливі наступні випадки:

Характер коренів		Часткові розв’язки
характеристич	-
		диференційного рівняння
ного рівняння

1. D > 0

≠ k

y = ek1 x ,

= ek2 x

2. D = 0

= k

y = ek1 x ,

= xek2 x

3. D < 0

k1,2 = α ± iβ

= eα x cos β x,

= eα x sin β x

Загальний розв’язок диференційного рівняння має вигляд

y = C1 y1 + C2 y2 ,

де

y1 , y2 - часткові

розв’язки диференційного

рівняння,

С1, С2 – свавільні постійні.

Приклад 16

y′′ − 5y′ + 6y = 0 .

Розв’язати рівняння

Складемо характеристичне рівняння:

k 2

− 5k + 6 = 0 .

Розв’язавши його отримаємо два корені

= 2,

= 3 , тоді

часткові розв’язки диференційного рівняння: y

= e2 x

= e3 x .

Отже загальний розв’язок диференційного рівняння має вигляд

y = C1e2 x + C2e3 x .

Приклад 17

y′′ + 6y′ + 9y = 0 .

Розв’язати рівняння

Складемо характеристичне рівняння:

k 2

+ 6k + 9 = 0 .

Розв’язавши його отримаємо два корені

k1 = k2

= −3 , тоді

часткові розв’язки диференційного рівняння:

y1 = e−3 x ,

y2 = xe−3 x .

Отже загальний розв’язок диференційного рівняння має вигляд

y = C1e−3 x + C2 xe−3 x .


Приклад 18	y′′ − 6y′ + 25y = 0 .
Розв’язати рівняння	y′′ − 6y′ + 25y = 0 .
Складемо характеристичне рівняння:		k 2	− 6k + 25 = 0 .
Розв’язавши його отримаємо два корені			k1,2 = 3 ± 4i , тоді

часткові розв’язки диференційного рівняння:

y1 = e3 x cos 4x, y2 = e3 x sin 4x .

Отже загальний розв’язок диференційного рівняння має вигляд

y = C1e3 x cos 4x + C2 e3 x sin 4x .

ЗАВДАННЯ 8.

Для функції z = x y + ln x :

а) Знайти частинні похідні I-го та II-го порядків;

б) Знайти градієнт у точці M 0 (1,1) та у загальному вигляді;

в) Знайти диференціал у точці M 0 (1,1) та у загальному вигляді.

Розв’язок

а) При обчисленні частинних похідних потрібно користуватися відомими правилами та формулами диференціювання функції однієї змінної, вважаючи при цьому другу змінну постійною.

Вважаючи змінну у сталою, отримаємо

z′	= y x y−1 +	1	1	= y x y−1 +	1	.
z′	= y x y−1 +			= y x y−1 +		.
x		x	y		x
		x	y		x
		y

Якщо вважати х сталою, отримаємо

		1		x			1
z′	= x y ln x +		−			= x y ln x −		.
z′	= x y ln x +		−		2	= x y ln x −		.
y		x		y	2		y
		x		y			y

Аналогічно обчислимо

z′′

= (z′ )′

= y ( y − 1) x y−2 −

;

z′′

= (z′ )′

= y x y−1 ln x + x y

= y x y−1 ln x + x y−1 ;

z′′

(z′

)′

1 x y−1

y x y−1 ln x

y x y−1

ln x

x y−1 ;

z′′

(z′

)′

ln x x y

ln x

x y ln2 x

+ y 2 =

+ y 2

y y

б)

Градієнтом

функції

z = f (x, y)

називається вектор,

координатами якого є частинні похідні цієї функції, тобто

grad z =

{z′

, z′

}= z′ i + z′

у нашому випадку

grad z = ( y x y−1 +

) i + (x y ln x −

)

а у точці M 0 (1,1) :

y−1

grad z(M 0 ) = y

i + x

M 0

= 1

i + 1

ln1

−

ln x − j =

y M 0

= 2 i − 1 j .

в) За означенням диференціал							dz	функції z = f (x, y)
обчислюється за формулою					dx + z′	dy .
	dz = z′				dx + z′	dy .
				x	y
Тоді у нашому випадку
	y−1		1			y			1
dz = y x		+			dx + x		ln x −			dy ,
dz = y x		+			dx + x		ln x −			dy ,
			x
			x						y

а у точці M 0 (1,1) :

dz(M 0 ) = 2 dx − 1 dy .

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.04.20192.06 Mб36Методики для курсовой.doc
#
16.07.2019383.49 Кб8методики по вниманию.doc
#
07.02.2016377.76 Кб56Методича по укр.мове.pdf
#
07.02.2016962.05 Кб23Методические материалы.doc
#
23.08.20194.69 Mб17методическое пособие новое.doc
#
07.02.2016276.95 Кб5Методичка 1807.pdf
#
08.11.2019229.89 Кб3методичка 2012 семенар КПЗС.doc
#
07.02.20164.06 Mб15Методичка Access.doc
#
07.05.20191.37 Mб2Методичка ІСуФУ 2007.doc
#
07.02.2016262.28 Кб7методичка ІУК.pdf
#
23.11.2019368.64 Кб3методичка банк. операции.doc