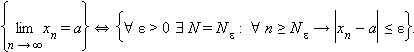9. Исправленная дисперсия
![]() (8)
(8)
10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:
![]() (9)
(9)
Среднее квадратическое отклонение называют также стандартным отклонением.
11. Коэффициент вариации V - это выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
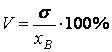 (10)
(10)
Дифференциал функции. Производные и дифференциалы высших порядков.
Дифференциалом
функции называется
линейная относительно ![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как ![]() или
или ![]() .
Таким образом:
.
Таким образом:
![]()
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производнойфункции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
Правило Лопиталя. Асимптоты, функции. Формула Лагранжа.
Правило
говорит, что если функции ![]() и
и ![]() обладают
следующим набором условий:
обладают
следующим набором условий:
-
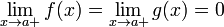 или
или 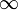 ;
; -
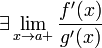 ;
; -
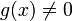 в
некоторой окрестности точки
в
некоторой окрестности точки 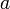 ,
,
тогда
существует ![]() .
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
.
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Вертикальной
асимптотой графика
функции ![]() называется
вертикальная прямая
называется
вертикальная прямая ![]() ,
если
,
если ![]() или
или ![]() при
каком-либо из условий:
при
каком-либо из условий: ![]() ,
, ![]() ,
, ![]() .
Заметим, что мы при этом не требуем,
чтобы точка
.
Заметим, что мы при этом не требуем,
чтобы точка ![]() принадлежала
области определения функции
принадлежала
области определения функции ![]() ,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки:
,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки: ![]() или
или ![]() ,
где
,
где ![]() .
Эта формула называется формулой
Лагранжа.
.
Эта формула называется формулой
Лагранжа.
![]()
Закон больших числ. Вывариваное, нормальное, показательное распределения.
Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.
Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.
|
Равномерное распределение Непрерывная случайная величина x , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения px (x) и функция распределения Fx (x) имеют соответственно вид:
Экспоненциальное (показательное) распределение Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения px (x )и функция распределения Fx (x) имеют соответственно вид:
Нормальное распределение Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике. Случайная величина x нормально распределена с параметрами a и s , s >0, если ее плотность распределения px (x ) и функция распределения Fx (x) имеют соответственно вид:
Часто используемая запись x ~ N(a, s ) означает, что случайная величина x имеет нормальное распределение с параметрами a и s . Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:
Здесь Функция
распределения нормальной величины x ~
N(a, s )
выражается через функцию Лапласа
следующим образом: Если x ~ N(a, s ), то случайную величину h = (x-a)/s называют стандартизованной илинормированной случайной величиной; h ~ N(0, 1) - имеет стандартное нормальное распределение |
Знакочередующиеся ряды. Признак Лейбница.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
![]()
Признак Лейбница
Основная статья: Теорема Лейбница о сходимости знакочередующихся рядов
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
|
Пусть для знакочередующегося ряда
выполняются следующие условия:
Тогда этот ряд сходится. |
Интегрирование заменой переменной, интегрирование по неопределенным интегралам.
Замена переменной в неопределенном интеграле
Одним
из наиболее мощных методов интегрирования
является замена
переменной в интеграле.
Поясним суть этого метода. Пусть ![]() ,
тогда
,
тогда
![]()
Но
в силу инвариантности формы дифференциала
равенство ![]() остается
справедливым и в случае, когда
остается
справедливым и в случае, когда ![]() —
промежуточный аргумент, т.е.
—
промежуточный аргумент, т.е. ![]() .
Это значит, что формула
.
Это значит, что формула ![]() верна
и при
верна
и при ![]() .
Таким образом,
.
Таким образом,
![]() ,
или
,
или ![]() .
.
Итак, если ![]() является
первообразной для
является
первообразной для ![]() на
промежутке
на
промежутке ![]() ,
а
,
а ![]() —
дифференцируемая на промежутке
—
дифференцируемая на промежутке ![]() функция,
значения которой принадлежат
функция,
значения которой принадлежат ![]() ,
то
,
то ![]() —
первообразная для
—
первообразная для ![]() , и,
следовательно,
, и,
следовательно,
![]()
Эта
формула позволяет свести вычисление
интеграла ![]() к
вычислению интеграла
к
вычислению интеграла ![]() .
При этом мы подставляем вместо
.
При этом мы подставляем вместо ![]() переменную
переменную ![]() ,
а вместо
,
а вместо ![]() дифференциал
этой переменной, т. е.
дифференциал
этой переменной, т. е. ![]() .
Поэтому полученная формула
называется формулой
замены переменной под знаком
неопределенного интеграла.
Она используется на практике как "слева
направо", так и "справа налево".
Метод замены переменной позволяет
сводить многие интегралы к табличным.
После вычисления интеграла
.
Поэтому полученная формула
называется формулой
замены переменной под знаком
неопределенного интеграла.
Она используется на практике как "слева
направо", так и "справа налево".
Метод замены переменной позволяет
сводить многие интегралы к табличным.
После вычисления интеграла ![]() надо
снова заменить
надо
снова заменить ![]() на
на ![]() .
.
Интегрирование ррациональных, тригонометрических иррациональных функций.
Интегрирование
рациональных функций - Функция ![]() называется
рациональной, если она вычисляется с
помощью четырех арифметических действий,
то есть в общем случае является частным
от деления двух многочленов:
называется
рациональной, если она вычисляется с
помощью четырех арифметических действий,
то есть в общем случае является частным
от деления двух многочленов: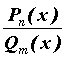 .
Если
.
Если ![]() ,
рациональная дробь называется
правильной. Неопределенный
интеграл от рациональной функции
всегда можно вычислить. Для этого:
,
рациональная дробь называется
правильной. Неопределенный
интеграл от рациональной функции
всегда можно вычислить. Для этого:
Если ![]() ,
выделяем целую часть рациональной
дроби с помощью деления многочлена на
многочлен. Правильную рациональную
дробь (или правильный остаток от деления)
раскладываем на простейшие дроби. Вид
разложения определяется корнями
многочлена
,
выделяем целую часть рациональной
дроби с помощью деления многочлена на
многочлен. Правильную рациональную
дробь (или правильный остаток от деления)
раскладываем на простейшие дроби. Вид
разложения определяется корнями
многочлена ![]() ,
а именно:
,
а именно:
Каждому
действительному корню![]() кратности
1 в разложении соответствует член
кратности
1 в разложении соответствует член 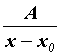 .
.
Каждому
действительному корню ![]() кратности
кратности ![]() в
разложении соответствует набор
из
в
разложении соответствует набор
из ![]() членов
членов
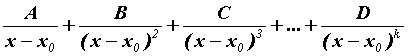 .
.
Каждой
паре комплексно сопряженных
корней ![]() кратности
1 в разложении соответствует член
кратности
1 в разложении соответствует член 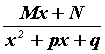 (
(![]() -
корни уравнения
-
корни уравнения ![]() ).
).
Каждой
паре комплексно сопряженных корней
кратности ![]() в
разложении соответствует набор
из
в
разложении соответствует набор
из ![]() членов
членов
 .
.
В
приведенных выражениях ![]() -
неопределенные коэффициенты, которые
можно найти, приводя разложение обратно
к общему знаменателю
-
неопределенные коэффициенты, которые
можно найти, приводя разложение обратно
к общему знаменателю ![]() ,
приравнивая полученные коэффициенты
при степенях
,
приравнивая полученные коэффициенты
при степенях ![]() к
соответствующим коэффициентам
к
соответствующим коэффициентам ![]() и
решая систему относительно
и
решая систему относительно ![]() .
.
Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы
вида 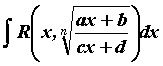 ,
где
,
где ![]() -
рациональная функция своих аргументов,
вычисляются заменой
-
рациональная функция своих аргументов,
вычисляются заменой  .
.
Интегралы
вида ![]() вычисляются
заменой
вычисляются
заменой ![]() или
или![]() .
.
Интегралы
вида ![]() вычисляются
заменой
вычисляются
заменой 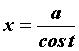 или
или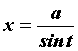 .
Интегралы вида
.
Интегралы вида ![]() вычисляются
заменой
вычисляются
заменой ![]() или
или![]() .
.
Матрицы основные понятия. Действия над матрицами.
Матрицей размера m на n (записывается так )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n
Действия над матрицами.
1. Сложение матриц - поэлементная операция
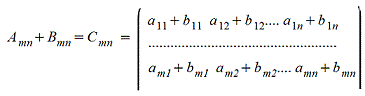
2. Вычитание матриц - поэлементная операция
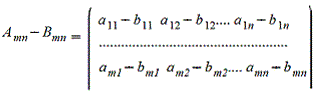
3. Произведение матрицы на число - поэлементная операция
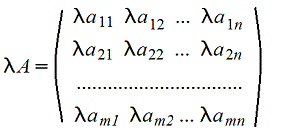
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
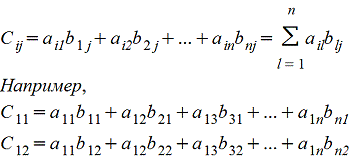
Множества. Функция, основные понятия.
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ... Существуют стандартные обозначения для некоторых множеств.Функция (или Функциональная зависимость) – это зависимость переменной y от переменной x. Это такая зависимость, при которой каждому значению переменной x соответствует только одно значение переменной y.Переменную x называют независимой переменной или аргументом.Переменную y называют зависимой переменной или функцией от переменной x.Значение независимой переменной называют абсциссой (горизонтальная плоскость графика).Соответствующее значение зависимой переменной называется ординатой (вертикальная плоскость графика).Совокупность значений независимой переменной называется областью определения функции.Совокупность значений зависимой переменной называют областью значений функции.График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.Значения аргумента, при которых функция обращается в нуль, называют нулями функции.
Невырожденные матрицы. Обратная матрица. Ранг матрицы.
Определение. Невырожденной
матрицей называется
квадратная матрица ![]() -го
порядка, определитель которой отличен
от нуля. В противном случае матрица
называется вырожденной.
-го
порядка, определитель которой отличен
от нуля. В противном случае матрица
называется вырожденной.
Определение. Матрицей,
союзной к матрице ![]() ,
называется матрица
,
называется матрица
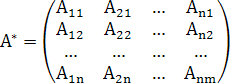 ,
,
где ![]() ij –
алгебраическое дополнение
элемента
ij –
алгебраическое дополнение
элемента ![]() ij данной
матрицы
ij данной
матрицы ![]() .
.
Напомним,
что матрица ![]() -1 называется
обратной матрице
-1 называется
обратной матрице ![]() ,
если выполняется условие
,
если выполняется условие ![]() -1
-1![]() -1
-1![]() ,
где
,
где ![]() –
единичная матрица того же порядка, что
и матрица
–
единичная матрица того же порядка, что
и матрица ![]() .
.
1.2.2. Обратная матрица
Теорема
(единственности
существования обратной матрицы): Если
у матрицы ![]() существует
обратная матрица
существует
обратная матрица ![]() ,
то она единственна.
,
то она единственна.
Доказательство.
Пусть
существует матрица ![]() ,
для которой
,
для которой ![]() и
матрица
и
матрица ![]() ,
для которой
,
для которой ![]() .
.
Тогда ![]() ,
то есть
,
то есть ![]() .
Умножим обе части равенства на матрицу
.
Умножим обе части равенства на матрицу ![]() ,
получим
,
получим ![]() ,
где
,
где ![]() и
и ![]() .
.
Значит, ![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Для
нахождения обратной матрицы ![]() применим алгоритм:
применим алгоритм:
1.Найдем
определитель матрицы ![]() и
убедимся, что он отличен от нуля, т.е.
матрица
и
убедимся, что он отличен от нуля, т.е.
матрица ![]() невырожденная
и имеет обратную матрицу
невырожденная
и имеет обратную матрицу ![]() .
.
2.Составим
союзную матрицу 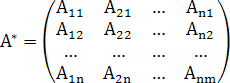 .
.
3.Найдем
произведение матриц![]() и
и ![]() Оно
равно
Оно
равно ![]() и
и ![]() .
.
4.Составим
обратную матрицу ![]()
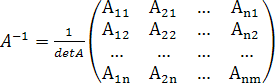 .
.
Свойства обратной матрицы:
1. ![]()
![]() .
.
2. ![]() .
.
3. ![]() .
.
Пример.
Найти обратную матрицу к матрице ![]() .
.
Решение.
1.
Найдем ![]() ,
следовательно матрица
,
следовательно матрица ![]() имеет
обратную.
имеет
обратную.
2.
Найдем алгебраические дополнения для
каждого элемента матрицы ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Cоставим
союзную матрицу ![]() .
.
3.
Найдем произведение матриц ![]() :
:
 .
.
Аналогично
проверим, что ![]() :
:
![]() .
.
4.
Составим обратную матрицу 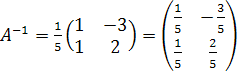 .
.
1.2.3. Ранг матрицы
Определение. В
матрице, состоящей из ![]() строк
и
строк
и ![]() столбцов,
вычеркнем некоторые строки и столбцы
так, чтобы число оставшихся строк и
столбцов стало одинаковым, например
столбцов,
вычеркнем некоторые строки и столбцы
так, чтобы число оставшихся строк и
столбцов стало одинаковым, например ![]() .
Из этих строк и столбцов составим
определитель. Этот определитель
называется минором
k-го порядка.
.
Из этих строк и столбцов составим
определитель. Этот определитель
называется минором
k-го порядка.
Количество
таких миноров определяется числами ![]() и
и ![]() ,
а наивысший порядок, который они могут
иметь, равен наименьшему из чисел
,
а наивысший порядок, который они могут
иметь, равен наименьшему из чисел ![]() и
и ![]() ,
то есть
,
то есть ![]() . Наименьший
порядок этих определителей равен
единице, причем определители первого
порядка суть сами элементы матрицы.
. Наименьший
порядок этих определителей равен
единице, причем определители первого
порядка суть сами элементы матрицы.
Предположим,
что все определители некоторого
порядка ![]() ,
входящие в матрицу, равны нулю. Тогда
все определители
,
входящие в матрицу, равны нулю. Тогда
все определители ![]() -го
порядка также равны нулю, так как всякий
определитель порядка
-го
порядка также равны нулю, так как всякий
определитель порядка ![]() можно
представить в виде суммы произведений
элементов его некоторой строки (столбца)
на алгебраические дополнения (а это
определители -го порядка) этих
элементов. Аналогично все определители
порядка
можно
представить в виде суммы произведений
элементов его некоторой строки (столбца)
на алгебраические дополнения (а это
определители -го порядка) этих
элементов. Аналогично все определители
порядка ![]() также
будут равны нулю. Это значит, что если
все определители -го порядка равны
нулю, то и все определители большего
порядка также равны нулю.
также
будут равны нулю. Это значит, что если
все определители -го порядка равны
нулю, то и все определители большего
порядка также равны нулю.
Определение.
В матрице порядка ![]() минор
порядка
минор
порядка ![]() называется
базисным, если он не равен нулю, а все
миноры порядка
называется
базисным, если он не равен нулю, а все
миноры порядка ![]() и
выше равны нулю, или не существуют
вовсе, т.е.
и
выше равны нулю, или не существуют
вовсе, т.е. ![]() совпадает с меньшим
из чисел
совпадает с меньшим
из чисел ![]() или
или ![]() .
.
Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
Определение.
Порядок базисного минора матрицы
называется рангом матрицы и
обозначается: ![]() или
или ![]() .
.
Можно использовать и другое определение ранга матрицы.
Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров.
Если ![]() ранг
матрицы равен
ранг
матрицы равен ![]() ,
то среди определителей порядка
,
то среди определителей порядка ![]() ,
входящих в эту матрицу, есть, по крайней
мере, один, отличный от нуля, но
определители матрицы
,
входящих в эту матрицу, есть, по крайней
мере, один, отличный от нуля, но
определители матрицы ![]() -го
порядка равны нулю.
-го
порядка равны нулю.
Ранг нулевой матрицы равен нулю, так как все миноры матрицы равны нулю.
Пример.
Найти ранг матрицы ![]() .
.
Решение.
Вычислим определитель матрицы ![]() ,
, ![]() .
.
Свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Еще
одним методом вычисления ранга матрицы
размера ![]() является метод
окаймляющих миноров.
является метод
окаймляющих миноров.
Суть
его в том, что для вычисления ранга
матрицы нужно найти хотя бы один ее
минор порядка ![]() отличный
от нуля, тогда ранг равен
отличный
от нуля, тогда ранг равен ![]() .
Если все ее миноры -го порядка равны
нулю, то следует рассматривать миноры
порядка
.
Если все ее миноры -го порядка равны
нулю, то следует рассматривать миноры
порядка ![]() и
так далее.
и
так далее.
Однако
на практике часто поступают наоборот
– переходят от миноров меньшего порядка
к минорам большего порядка. Если найден
минор -го порядка отличный от нуля,
то вычисляют только миноры ![]() -го
порядка которые являются окаймлением
найденного минора
-го
порядка которые являются окаймлением
найденного минора ![]() -го
порядка. Если все такие миноры равны
нулю, то ранг матрицы равен
-го
порядка. Если все такие миноры равны
нулю, то ранг матрицы равен ![]() .
.
Пример.
Найти ранг матрицы 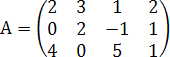 ,
выполнив элементарные преобразования
и получив эквивалентную матрицу.
,
выполнив элементарные преобразования
и получив эквивалентную матрицу.
Решение.

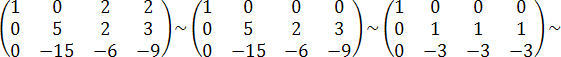
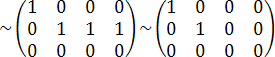
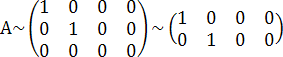 .
В последней матрице есть минор 2-го
порядка отличный от нуля,
.
В последней матрице есть минор 2-го
порядка отличный от нуля, ![]() , значит
, значит ![]() .
.
Несобственные интегралы. Формула Ньютона – Лейбница
. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ:
I рода:![]() =
= ![]() ;
; ![]()
![]() ;
;![]()
II рода: ![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
= 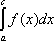 +
+ 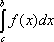
I.Определенный интеграл:
Формула Ньютона-Лейбница:
Если
для непрерывной на отрезке [а;b] функции f(x) может
быть найдена ее первообразная F(x), то
простым и удобным методом вычисления
определенного интеграла 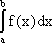 является формула
Ньютона-Лейбница:
является формула
Ньютона-Лейбница: ![]()
При интегрировании четных и нечетных функций в симметричных пределах интегрирования полезно использовать формулу:
![]()
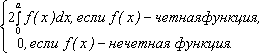
Общие сведения о дифференциальных уравнениях. Основные понятия. Задача Коши
Дифференциа́льное
уравне́ние — уравнение,
связывающее значение некоторой
неизвестной функции в
некоторой точке и значение
её производных различных
порядков в той же точке. Дифференциальное
уравнение содержит в своей записи
неизвестную функцию, её производные и
независимые переменные; однако не любое
уравнение, содержащее производные
неизвестной функции, является
дифференциальным уравнением.
Например, ![]() не
является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные,
но обязано содержать хотя бы одну из
производных.
не
является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные,
но обязано содержать хотя бы одну из
производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением
(интегралом)
дифференциального
уравнения порядка n называется функция y(x),
имеющая на некотором интервале (a,
b) производные ![]() до
порядка n включительно
и удовлетворяющая этому уравнению.
Процесс решения дифференциального
уравнения называется интегрированием.
Вопрос об интегрировании дифференциального
уравнения считается решенным, если
нахождение неизвестной функции удается
привести к квадратуре,
независимо от того, выражается ли
полученный интеграл в конечном виде
или нет.
до
порядка n включительно
и удовлетворяющая этому уравнению.
Процесс решения дифференциального
уравнения называется интегрированием.
Вопрос об интегрировании дифференциального
уравнения считается решенным, если
нахождение неизвестной функции удается
привести к квадратуре,
независимо от того, выражается ли
полученный интеграл в конечном виде
или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
![]() или
или ![]() ,
,
где ![]() —
неизвестная функция (возможно, вектор-функция;
в таком случае часто говорят о системе
дифференциальных уравнений), зависящая
от независимой переменной
—
неизвестная функция (возможно, вектор-функция;
в таком случае часто говорят о системе
дифференциальных уравнений), зависящая
от независимой переменной ![]() ,
штрих означает дифференцирование по
,
штрих означает дифференцирование по ![]() .
Число
.
Число ![]() называется порядком дифференциального
уравнения.
называется порядком дифференциального
уравнения.
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
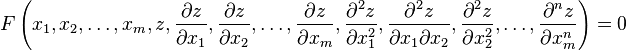 ,
,
где ![]() —
независимые переменные, а
—
независимые переменные, а ![]() —
функция этих переменных.
—
функция этих переменных.
Различные постановки задачи Коши
-
ОДУ первого порядка, разрешённое относительно производной
![]()
-
Система
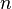 ОДУ первого
порядка, разрешённая относительно
производных (нормальная
система
ОДУ первого
порядка, разрешённая относительно
производных (нормальная
система  -го
порядка)
-го
порядка)

-
ОДУ
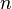 -го
порядка, разрешённое относительно
старшей производной
-го
порядка, разрешённое относительно
старшей производной
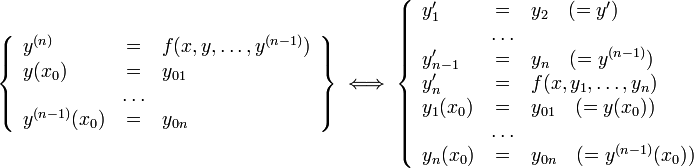
Однородные дифференциальные уравнения. Уравнения с разделяющимися переменными
Определение однородного дифференциального уравнения
Дифференциальное уравнение первого порядка
![]()
называется однородным, если правая часть удовлетворяет соотношению
![]()
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
![]()
Однородное дифференциальное уравнение можно также записать в виде
![]()
или через дифференциалы:
![]()
где P(x,y) и Q(x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
![]()
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
![]()
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
![]()
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
![]()
где p(x) и h(y) −
непрерывные функции.
Рассматривая
производную y' как
отношение дифференциалов ![]() ,
перенесем dx в
правую часть и разделим уравнение
на h(y):
,
перенесем dx в
правую часть и разделим уравнение
на h(y):
![]()
Разумеется,
нужно убедиться, что h(y)
≠ 0. Если найдется число x0,
при котором h(x0)
= 0, то это число будет также являться
решением дифференциального уравнения.
Деление на h(y) приводит
к потере указанного решения.
Обозначив ![]() ,
запишем уравнение в форме:
,
запишем уравнение в форме:
![]()
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
![]()
где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение
![]()
описывающее общее решение уравнения с разделяющимися переменными
Определение производной; ее механический и геометрический смысл. Производная сложной, обратной , неявной функции.
Производная. Рассмотрим
некоторую функцию y = f ( x )
в двух точках x0
и x0 + ![]() : f ( x0 )
и f ( x0 +
: f ( x0 )
и f ( x0 + ![]() ). Здесь через
). Здесь через ![]() обозначено некотороемалое изменение
аргумента, называемое приращением
аргумента;
соответственно разность между двумя
значениями
функции: f ( x0 +
обозначено некотороемалое изменение
аргумента, называемое приращением
аргумента;
соответственно разность между двумя
значениями
функции: f ( x0 + ![]() ) - f ( x0 )называется приращением
функции. Производной функции y = f ( x )
в точке x0 называется
предел:
) - f ( x0 )называется приращением
функции. Производной функции y = f ( x )
в точке x0 называется
предел:
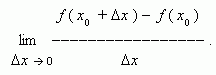
Если этот предел существует, то функция f ( x ) называется дифференцируемой в точке x0 . Производная функции f ( x ) обозначается так:
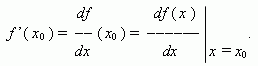
Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
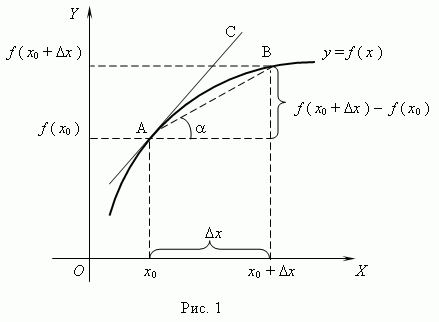
Из рис.1 видно, что для любых двух точек A и B графика функции:
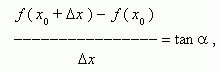
где ![]() - угол
наклона секущей AB.
- угол
наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей. Если
зафиксировать точку A и двигать
по направлению к ней точкуB,
то ![]() неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке. В
этом и состоит геометрический
смысл производной.
неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке. В
этом и состоит геометрический
смысл производной.
Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x0 , f ( x0 ) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x0 ) имеет вид:
y = f ’( x0 ) · x + b .
Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:
f ( x0 ) = f ’( x0 ) · x0 + b ,
отсюда, b = f ( x0 ) – f ’( x0 ) · x0 , и подставляя это выражение вместо b, мы получим уравнение касательной:
y = f ( x0 ) + f ’( x0 ) · ( x – x0 ) .
Механический
смысл производной. Рассмотрим
простейший случай: движение материальной
точки вдоль координатной оси, причём
закон движения задан: координата x
движущейся точки – известная
функция x ( t )
времени t.
В течение интервала времени от t0
до t0 + ![]() точка
перемещается на расстояние: x ( t0 +
точка
перемещается на расстояние: x ( t0 + ![]() ) - x ( t0 )
=
) - x ( t0 )
= ![]() ,
а её средняя
скорость равна: va =
,
а её средняя
скорость равна: va = ![]() /
/ ![]() . При
. При ![]()
![]() 0
значение средней скорости стремится
к определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
0
значение средней скорости стремится
к определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
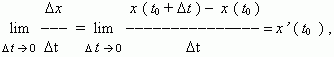
отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
Пусть
теперь задана сложная
функция ![]() ,
т.е. переменная
,
т.е. переменная ![]() есть
функция переменной
есть
функция переменной ![]()
![]() ,
а переменная
,
а переменная ![]() есть,
в свою очередь, функция от независимой
переменной
есть,
в свою очередь, функция от независимой
переменной ![]() .
.
Теорема. Если ![]() и
и ![]() - дифференцируемые функции
своих аргументов, то сложная
функция
- дифференцируемые функции
своих аргументов, то сложная
функция ![]() является
дифференцируемой функцией и ее
производная равна произведению
производной данной функции по
промежуточному аргументу и производной
промежуточного аргумента по
независимой переменной:
является
дифференцируемой функцией и ее
производная равна произведению
производной данной функции по
промежуточному аргументу и производной
промежуточного аргумента по
независимой переменной:
![]() .
Утверждение
легко получается из очевидного
равенства
.
Утверждение
легко получается из очевидного
равенства ![]() (справедливого
при
(справедливого
при ![]() и
и ![]() )
предельным переходом при
)
предельным переходом при ![]() (что
в силу непрерывности дифференцируемой
функции влечет
(что
в силу непрерывности дифференцируемой
функции влечет ![]() ).
).
Перейдем к рассмотрению производной обратной функции.
Пусть
на множестве ![]() дифференцируемая
функция
дифференцируемая
функция ![]() имеет
множество значений
имеет
множество значений ![]() и
на множестве
и
на множестве ![]() существует обратная
функция
существует обратная
функция ![]() .
.
Теорема. Если
в точке ![]() производная
производная ![]() ,
то производная обратной функции
,
то производная обратной функции ![]() в
точке
в
точке ![]() существует
и равна обратной величине производной
данной функции:
существует
и равна обратной величине производной
данной функции:  ,
или
,
или
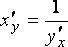 .
.
Эта формула легко получается из геометрических соображений.
Так
как ![]() есть
тангенс угла наклона касательной
линии
есть
тангенс угла наклона касательной
линии ![]() к
оси
к
оси ![]() ,
то
,
то ![]() есть
тангенс угла наклона той же касательной
(той же линии
есть
тангенс угла наклона той же касательной
(той же линии ![]() )
в той же точке
)
в той же точке ![]() к
оси
к
оси ![]() .
. 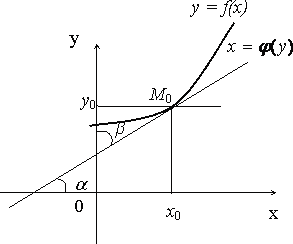
Если ![]() и
и ![]() острые,
то
острые,
то 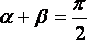 ,
а если тупые, то
,
а если тупые, то 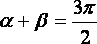 .
.
В
обоих случаях 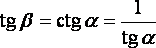 .
Этому равенству и равносильно равенство
.
Этому равенству и равносильно равенство
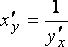 .
.
Во многих задачах функция y(x) задана невным образом. Например, для приведенных ниже функций
![]()
невозможно получить зависимость y(x) в явном виде. Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом:
-
Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;
• Решить полученное уравнение относительно производной y'(x).
Определенный интеграл, основные свойства и вычисление.
Понятие определённого интеграла
Определённым
интегралом от непрерывной функции f(x)
на конечном отрезке [a, b]
(где ![]() )
называется приращение какой-нибудь её
первообразной на этом отрезке. При этом
употребляется запись
)
называется приращение какой-нибудь её
первообразной на этом отрезке. При этом
употребляется запись
![]()
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
![]()
При a = b по определению принимается
![]()
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
![]()
Поэтому формулу Ньютона-Лейбница будем записывать и так:
![]()
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) =F(x) + C. Поэтому
![]()
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Из всех первообразных для f(x) выбирается обычно та, которая соответствует равной нулю производной постоянной, и к ней применяется формула Ньютона-Лейбница.
Свойства определённого интеграла
Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
![]()
Это
свойство содержится в самом определении
определённого интеграла. Однако его
можно получить и по формуле
Ньютона-Лейбница:
![]()
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
![]()
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,
![]()
На основании формулы (39) последнее равенство означает равенство интегралов
![]()
и
![]()
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
![]()
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
![]()
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
![]()
то
![]()
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
![]()
Теорема
7 (теорема
о среднем). Определённый
интеграл равен произведению длины
отрезка интегрирования на значение
подынтегральной функции в некоторой
точке  внутри
его, т.е.
внутри
его, т.е.
![]()
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
![]()
Теорема
9. Если
верхний предел интегрирования больше
нижнего и функции ![]() и
и ![]() непрерывны,
то неравенство
непрерывны,
то неравенство
![]()
можно почленно интегрировать, т.е.
![]()
Первообразная и неопределенный интеграл. Основные свойства.
Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции
F'(x) = f(x).
Обозначение
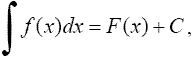
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением. 1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
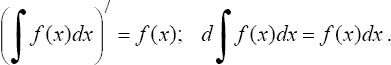
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
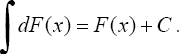
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
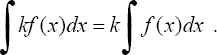
Первые, вторые замечательные пределы. Непрерывность функции в точке и на отрезке.
Первый замечательный предел
![]()
Второй замечательный предел
![]() или
или ![]()
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
![]()
Тот
же факт можно записать иначе: ![]()
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Последовательность, предел. Числовые последовательности. Предел функции.
Если
каждому натуральному числу n поставлено
в соответствие некоторое вещественное
число ![]() то говорят, что задана числовая
последовательность
то говорят, что задана числовая
последовательность ![]() Кратко
она обозначается символом
Кратко
она обозначается символом ![]()
![]() называют n-м
членом последовательности.
Совокупность этих чисел называют
множеством значений последовательности.
называют n-м
членом последовательности.
Совокупность этих чисел называют
множеством значений последовательности.
Существует несколько способов задания числовых последовательностей.
-
Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например,
 ).
). -
Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая и геометрическаяпрогрессии или, например, последовательность Фибоначчи, задаваемая формулой
xn + 2 = xn + 1 + xn при n > 0
-
и условиями x1 = 1, x2 = 1.
-
Иногда последовательность задается описанием ее членов, например, последовательность, у которой xn равен n-му знаку после запятой в десятичной записи числаπ = 3,14159265358979323..., задается следующим образом: x1 = 1, x2 = 4, x3 = 1, x4 = 5, x5 = 9, x6 = 2, x7 = 6, x8 = 5, x9 = 3, x10 = 5 и т. д.
Число a называется пределом последовательности {xn}, если для каждого ε > 0 существует такой номер Nε, что для всех n ≥ Nε выполняется неравенство
|
|xn – a| < ε, |
т. е. ![]() При
этом пишут, что
При
этом пишут, что 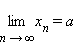 или
или ![]() при n → ∞.
Кратко это определение можно записать
так:
при n → ∞.
Кратко это определение можно записать
так:
|
|
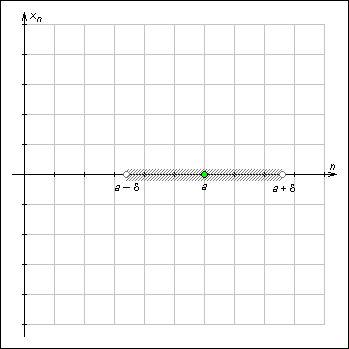
Интервал (a – ε; a + ε) называют ε-окрестностью точки a.
|
|
|
Рисунок 1.1.1.1. ε-окрестность точки a. |
Так,
если 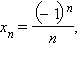 то
то ![]() Действительно,
выбрав для произвольного ε > 0
Действительно,
выбрав для произвольного ε > 0 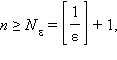 получаем
получаем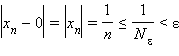 ,
так как
,
так как 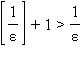 .
Здесь существенно, что Nε зависит
от ε.
.
Здесь существенно, что Nε зависит
от ε.
Для стабилизирующейся последовательности (т. е. последовательности {xn} такой, что xn = a при n ≥ n0) в качестве Nεдля любого ε можно взять n0.
Последовательность, у которой существует предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся.
Можно показать, что числовая последовательность имеет только один предел.
Последовательность ![]() называется возрастающей,
если для любого
называется возрастающей,
если для любого ![]() выполняется
неравенство
выполняется
неравенство
|
xn + 1 > xn. |
Последовательность ![]() называется убывающей,
если для любого
называется убывающей,
если для любого ![]() выполняется
неравенство
выполняется
неравенство
|
xn + 1 < xn. |
Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей.
Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.
Последовательности. Рассмотрим ряд натуральных чисел:
1, 2, 3, … , n –1, n, … .
Если заменить каждое натуральное число n в этом ряду некоторым числом un , следуя некоторому закону, то мы получим новый ряд чисел:
u1 , u2 , u3 , …, un - 1 , un , …, кратко обозначаемый { un }
и называемый числовой последовательностью. Величина un называется общим членом последовательности. Обычно числовая последовательностьзадаётся некоторой формулой un = f ( n ), позволяющей найти любой член последовательности по его номеру n ; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).
П р и м е р ы числовых последовательностей:
1, 2, 3, 4, 5, … - ряд натуральных чисел ;
2, 4, 6, 8, 10, … - ряд чётных чисел;
1.4, 1.41, 1.414, 1.4142, … - числовая последовательность
приближённых
значений ![]()
с увеличивающейся точностью.
В последнем примере невозможно дать формулу общего члена последовательности, тем не менее эта последовательность писана полностью.
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a приувеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгоеопределение.
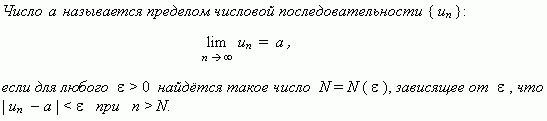
Это
определение означает, что a
есть предел числовой
последовательности, если её общий член
неограниченно приближается к a
при возрастании n.
Геометрически это значит, что для
любого ![]() >
0 можно найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a -
>
0 можно найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a - ![]() , a +
, a + ![]() ).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
Последовательность
называется ограниченной,
если существует такое число M,
что | un
| ![]() M для
всех n . Возрастающая
или убывающая последовательность
называется монотонно
M для
всех n . Возрастающая
или убывающая последовательность
называется монотонно
Признаки сходимости знакоположительных рядов.
Теорема (первый
признак сравнения). Даны
числовые ряды ![]() и
и ![]() ,
где
,
где ![]()
Тогда:
-
Если ряд
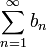 -
сходится, то
-
сходится, то 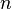 ряд
ряд 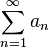 сходится.
сходится. -
Если ряд
 -
расходится, то и ряд
-
расходится, то и ряд 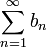 расходится.
расходится.
Теорема (второй
признак сравнения). Даны
числовые ряды ![]() ,
, ![]() ,
, ![]()
Пусть ![]() ,
тогда ряды сходятся или расходятся
одновременно.
,
тогда ряды сходятся или расходятся
одновременно.
Признак Даламбера
Теорема (признак
Даламбера). Дан
ряд ![]() .
Пусть
.
Пусть ![]() ,
тогда
,
тогда
-
Если
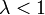 -
ряд сходится
-
ряд сходится
Если ![]() -
ряд расходится
-
ряд расходится
Системы линейных алгебраических уравнений.
Совокупность уравнений
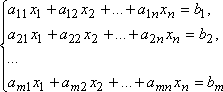
относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Система линейных уравнений может быть записана в матричной форме A·x = b:
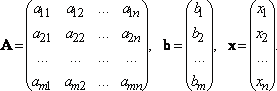
Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
A(1)x1 + A(2)x2 + ... + A(n)xn = b. Здесь A(1), A(2), ... , A(n) — столбцы матрицы системы.
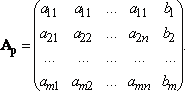
Матрица Ap называется расширенной матрицей системы.
Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.
Скалярное, векторное, смешанное произведение векторов и их свойства.
Скалярное
произведение векторов —
это число, равное произведению длин
этих векторов на косинус угла между
ними.
![]()
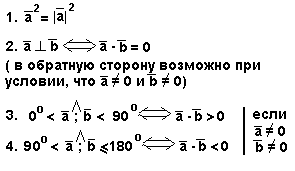
Скалярное произведение векторов через их координаты

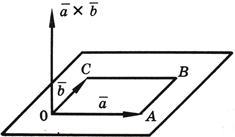
Векторным
произведением векторов ![]() и
и ![]() называется
вектор
называется
вектор ![]() ,
который определяется следующими
условиями:
,
который определяется следующими
условиями:
1)
Его модуль равен ![]()
![]() где
где ![]() -
угол между векторами
-
угол между векторами ![]() и
и ![]() .
.
2)
Вектор ![]() перпендикулярен
к плоскости, определяемой перемножаемыми
векторами
перпендикулярен
к плоскости, определяемой перемножаемыми
векторами ![]() и
и ![]() .
.
3)
Вектор ![]() направлен
так, что наблюдателю, смотрящему с его
конца на перемножаемые векторы
направлен
так, что наблюдателю, смотрящему с его
конца на перемножаемые векторы ![]() и
и ![]() ,
кажется, что для кратчайшего совмещения
первого сомножителя со вторым первый
сомножитель нужно вращать против
часовой стрелки (см. рисунок).
,
кажется, что для кратчайшего совмещения
первого сомножителя со вторым первый
сомножитель нужно вращать против
часовой стрелки (см. рисунок).
Векторное
произведение векторов ![]() и
и ![]() обозначается
символом
обозначается
символом ![]() :
:
![]()
![]()
![]()
![]() (25)
(25)
или
![]()
![]()
![]() (26)
(26)
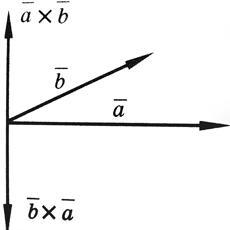
Основные свойства векторного произведения:
1)
Векторное произведение ![]() равно
нулю, если векторы
равно
нулю, если векторы ![]() и
и ![]() коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):
![]()
![]()
![]()
Векторное произведение не обладает свойством переместительности.
Смешанным
произведением трех векторов ![]() ,
, ![]() ,
, ![]() называется
число, равное скалярному произведению
вектора
называется
число, равное скалярному произведению
вектора ![]() на
вектор
на
вектор ![]() :
: ![]()
Случайная величина. Закон распределения вероятностей дискретной случайной величины. Формулы для вычисления основных числовых характеристик непрерывной случайной величины.
Случайная величина называется дискретной, если ее множество значений счетно.
Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий вместе с алгеброй событий и вероятностью образует тройку , которая называется вероятностным пространством.
Непрерывные случайные величины. Плотность вероятности.
Случайная
величина ![]() называется непрерывной,
если ее функция распределения
F(x) непрерывна на всей числовой оси.
называется непрерывной,
если ее функция распределения
F(x) непрерывна на всей числовой оси.
Для непрерывной
случайной величины ![]() при
любом
при
любом ![]() имеет
место равенство
имеет
место равенство
![]()
а также
![]()
где F(x)
функция распределения величины ![]() .
.
Пусть f(x) - неотрицательная интегрируемая функция, определенная на всей числовой оси и удовлетворяющая условию
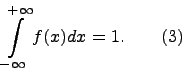
Тогда функция
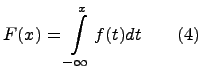
обладает
всеми свойствами функции
распределения. Кроме
того, F(x)
непрерывна в любой точке (и слева, и
справа). Следовательно,
случайная величина ![]() ,
определяемая функцией распределения
F(x),
является непрерывной.
,
определяемая функцией распределения
F(x),
является непрерывной.
Мы
говорим, что случайная
величина ![]() с функцией
распределения F(x) раcпределена
сплотностью,
если существует неотрицательная
функция f(x),
такая, что для любого
с функцией
распределения F(x) раcпределена
сплотностью,
если существует неотрицательная
функция f(x),
такая, что для любого ![]() имеет
место равенство (2). При этом f(x)
называется плотностью вероятности
случайной величины
имеет
место равенство (2). При этом f(x)
называется плотностью вероятности
случайной величины ![]() ,
а ее график – кривой
распределения.
,
а ее график – кривой
распределения.
Из
определения плотности
вероятности f(x) и
свойств функции
распределения следует,
что f(x) должна
удовлетворять условию (1). И обратно,
если ![]() и
выполняется условие (1), то f(x)
является плотностью вероятности.
и
выполняется условие (1), то f(x)
является плотностью вероятности.
Если случайная
величина ![]() имеет плотность
вероятности f(x) ,
то имеет место формула
имеет плотность
вероятности f(x) ,
то имеет место формула
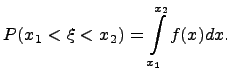
Числовые ряды. Основные понятия. Необходимый признак сходимости числового ряда
Пусть
положительные числа ![]() -
члены некоторой бесконечной числовой
последовательности. Тогда выражение
вида
-
члены некоторой бесконечной числовой
последовательности. Тогда выражение
вида
![]() (1)
(1)
называется числовым рядом.
Здесь ![]() –
общий член ряда, с помощью которого ряд
(1) записывается в виде
–
общий член ряда, с помощью которого ряд
(1) записывается в виде
![]()
Зная
общий член ряда, можно записать ряд в
форме (1). Так общим членом ![]() задается числовой ряд
задается числовой ряд
![]()
Рассмотрим для числового ряда (1) суммы его первых членов
![]()
Будем называть их частичными суммами и обозначим соответственно через
![]()
Если для некоторого числового ряда бесконечная последовательность его частичных сумм имеет конечный предел, то этот ряд называется сходящимся.
Этот
предел ![]() называется
суммой ряда.
называется
суммой ряда.
Если последовательность частичных сумм ряда не имеет определенного предела, то ряд называется расходящимся и для него не существует суммы.
Рассмотрим примеры на исследование сходимости ряда по определению.
Пример 1.
Дан ряд
![]()
Это
геометрическая прогрессия с первым
членом ![]() и
знаменателем
и
знаменателем ![]() .
.
Частичная сумма ряда
![]() или
или ![]() .
.
1)
если ![]() ,
то
,
то ![]() ,
при
,
при ![]() и,
следовательно,
и,
следовательно,
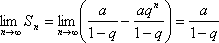
Значит,
в случае ![]() ряд
сходится и его сумма
ряд
сходится и его сумма ![]() .
.
2)
если ![]() ,
то
,
то ![]() ,
при
,
при ![]() и
тогда
и
тогда ![]() ,т.е.
,т.е. ![]() не
существует и ряд расходится
не
существует и ряд расходится
3)
если ![]() то
данный ряд имеет вид
то
данный ряд имеет вид
![]()
В
этом случае ![]() ,
т.е. ряд расходится.
,
т.е. ряд расходится.
4)
если ![]() ,
то имеем ряд
,
то имеем ряд
![]()
В
этом случае ![]()
Следовательно, ![]() предела
не имеет и ряд расходится
предела
не имеет и ряд расходится
Таким
образом, ряд ![]() сходится
только тогда, когда знаменатель
прогрессии по абсолютной величине
меньше единицы.
сходится
только тогда, когда знаменатель
прогрессии по абсолютной величине
меньше единицы.
Пример 2.
Рассмотрим ряд
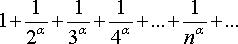 ,
,
который называется обобщенным гармоническим рядом.
1)
пусть![]()
Составим n-ю частичную сумму
![]()
По
условию ![]() ,
т.о.
,
т.о.
![]() ,
следовательно, ряд расходится
,
следовательно, ряд расходится
2)
при ![]()
![]() и
ряд будет сходящимся.
и
ряд будет сходящимся.
т.о.
обобщенный гармонический ряд ![]() расходится
при
расходится
при ![]() и
сходится при
и
сходится при ![]() .
.
При ![]() получим
ряд вида
получим
ряд вида ![]() ,
который называется гармоническим и
является расходящимся рядом.
,
который называется гармоническим и
является расходящимся рядом.
Пример 3.
Рассмотрим ряд
![]()
Общий член заданного ряда может быть представлен в виде:
![]() ,
сравнив числители дробей, получим
значения
,
сравнив числители дробей, получим
значения ![]() ,
, ![]() и,
таким образом,
и,
таким образом, 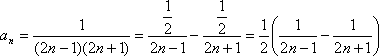
Определим
частичную сумму ряда 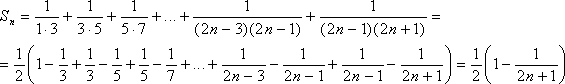
Отсюда ![]() ,
и, таким образом, заданный ряд сходится.
,
и, таким образом, заданный ряд сходится.
Для рассмотренных рядов операция суммирования оказалась сравнительно несложной. Вообще же этот прием, если он и выполним, связан со сложными вычислениями. Поэтому для исследования характера ряда применяют признаки сходимости.
2. Необходимый признак сходимости.
Теорема.
Если
числовой ряд ![]() сходится,
то его общий член при неограниченном
возрастании n стремится
к нулю, т.е.
сходится,
то его общий член при неограниченном
возрастании n стремится
к нулю, т.е.
![]()
Доказательство.
Пусть данный ряд сходится. Тогда по определению сходящегося ряда
![]() ;
;
так
как вместе с ![]() также
и
также
и ![]() ,
то
,
то ![]() ,
т.е.
,
т.е.
![]()
Здесь ![]() ,
а
,
а ![]() .
.
Поэтому ![]()
Отсюда ![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Элементы комбинаторики . Формула Бернулли.
Элементы комбинаторики.
Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.
Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать kспособами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.
Размещение
с повторением. Из
множества, содержащего m элементов,
нужно выбрать k элементов,
причем выбранный элемент, после того,
как его взяли, вновь возвращается в
исходное множество (то есть элементы
в выбранном множестве могут повторяться).
Пользуясь правилом произведения,
получим, что каждый из k элементов
может быть выбран m способами.
Таким образом, общее число комбинаций
равно ![]() .
.
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Решение. Первой
цифрой в числе может быть любая из
четырех имеющихся. То же самое можно
сказать и о последующих цифрах числа,
поэтому общее число комбинаций: ![]()
Размещение
без повторений.
Из множества, содержащего m различных
элементов, надо выбрать упорядоченное
подмножество из kэлементов
(k£m),
то есть такое подмножество, в котором
элементы располагаются в определенном
порядке, и изменение порядка элементов
изменяет подмножество. Кроме этого,
элементы в выбранном подмножестве не
повторяются. Требуется выяснить, сколько
таких комбинаций существует. По правилу
произведения получаем, что первый
элемент можно выбрать m способами,
второй элемент – (m-1)
способом, и так далее, а элемент с
номером k можно
выбрать (m – k +
1) способами. Следовательно, число
упорядоченных k-элементных
подмножеств, взятых из множества,
содержащего m элементов
равно m(m-1)(m-2)…(m-k+1).
Такие подмножества называются
размещениями из m элементов
по k элементов,
а их общее число можно выразить
формулой 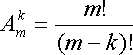 .
.
Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?
Решение. Общее
число комбинаций равно числу размещений
из 6 элементов по 4: 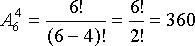
Перестановки. Пусть
множество содержит m различных
элементов. Рассмотрим все возможные
варианты перестановок элементов этого
множества. Получаемые при этом
упорядоченные множества отличаются
друг от друга только порядком входящих
в них элементов. Такие упорядоченные
множества называются перестановками.
Число перестановок из m элементов
равно: ![]()
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?
Решение. Количество
чисел равно числу перестановок из
четырех элементов: ![]()
Сочетания. Пусть
из множества, содержащего m различных
элементов, требуется выбрать подмножество,
содержащее k различных
элементов (k £ m).
Получаемые при этом подмножества не
упорядочены. Такие неупорядоченные
подмножества называются сочетаниями.
Число сочетаний изm элементов
по k элементов
вычисляется по формуле: 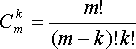
Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Решение. Число
способов равно числу сочетаний из 10
элементов по 3 элемента: 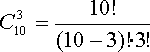 .
.
Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна:
Pn(k)=Cnkpkqn-k
или
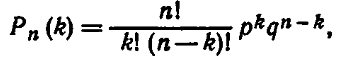
где q=1-p
Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, — находят соответственно по формулам:
Pn(0)+Pn(1)+...+Pn(k-1);
Pn(k+1)+Pn(k+2)+...+Pn(n);
Pn(k)+Pn(k+1)+...+Pn(n);
Pn(0)+Pn(1)+...+Pn(k);

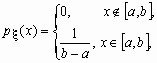
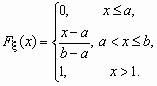
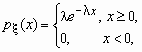
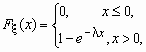
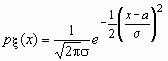 ,
,  , Mx =
a, Dx = s 2.
, Mx =
a, Dx = s 2.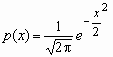 ,
, 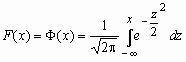 , Mx =
0, Dx =
1.
, Mx =
0, Dx =
1.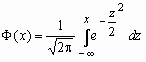 -
функция Лапласа.
-
функция Лапласа.