
NEWsbornik
.pdf
179.o R1 = {(x, y) | 0 6 x 6 1, 0 6 y 6 1 − x} R × R, R2 = {(y, z) | 0 6 y 6 1, 1 − y 6 z 6 1} R × R.
Пусть R, R , R
ждения 180 185. 2 бинарные отношения. Докажите утвер-
180. R ◦ (R1 R2) = (R ◦ R1) (R ◦ R2).
181.o (R1 R2) ◦ R = (R1 ◦ R) (R2 ◦ R).
182. R ◦ (R1 ∩ R2) (R ◦ R1) ∩ (R ◦ R2). 183.o (R1 ∩ R2) ◦ R (R1 ◦ R) ∩ (R2 ◦ R). 184.o (R ◦ R1) \ (R ◦ R2) R ◦ (R1 \ R2). 185.o (R1 ◦ R) \ (R2 ◦ R) (R1 \ R2) ◦ R.
186. Пусть R1, R2 бинарные отношения, докажите, что
DR1◦R2 = R1−1(M), ãäå M = VR1 ∩ DR2 .
187.o Пусть R1, R2 бинарные отношения, докажите, что
VR1◦R2 = R2(M), ãäå M = VR1 ∩ DR2 .
Отношения эквивалентности и порядка
à)188рефлексивно,. Постройте симметрично,бинарноеотношениено не транзитивно,на M = {a, b, c}, которое
б) антисимметрично, транзитивно, но не рефлексивно.
o
à)189рефлексивно,. Постройтетранзитивно,бинарноеотношениено не симметрично,на M = {a, b, c}, которое
б) симметрично, транзитивно, но не рефлексивно. отношение190. ПустьнаRмножестве= {(x, y) | y = x + 1, x = 1, 2, . . . , n −1} бинарное ное, симметричное и рефлексивноеM = {1, 2замыкания, . . . , n}. Найдитеотношениятранзитив-
R.
191. Приведите пример симметричных отношений R1 è R2 íà
A = {1, 2, 3}, композиция которых несимметрична. Докажите следующие утверждения (192 200).
192.Åñëè R A × B , òî R ◦ R−1 симметрично.
193.Åñëè R симметрично, то R ◦ R тоже симметрично.
16
ОТВЕТЫ И УКАЗАНИЯ
2. x = y = 1. 13. à) |
x |
(y z), á) |
|
x |
yz , â) x(y |
z |
|
x |
|
t |
). |
|
|
14. à) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
y |
, á) |
|
x |
|
|
y |
, â) |
|
|
|
x |
|
y. |
15. à) |
|
x = 1, y = 0, |
|
z = 1; á) |
|
x = 1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
yНапример,= 0, z = 0. 16. a b = |
|
a |
· |
|
|
|
|
|
|
|
|
|
17. ab = |
|
a |
|
|
. 21. à) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
. |
|
|
|
b |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a = 0, b = 1; á) a = 0, b è c любые; в) a = b = c = 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
24. |
|
a = 0, b è c любые. |
|
|
|
29. ab = (a → (b → 0)) → 0. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
произвольную30. a b = (a →формулуb) → b. |
|
|
|
32. Указание. Рассмотрите ab è |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(a, b, →) на строчках (0; 0), (0; 1) è |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(1; 0). |
33. y 1. 34. xy x y 1. 35. xy x z 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
36. |
|
xyz x y z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
37. |
|
xyzt yzt xzt xyt xyz xy xz yt 1. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
38. |
|
xyz xy xz yz y z 1. 39. xyz xy yz y 1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
40. |
abcd abc abd acd bcd ab ac ad bc cd bd a b c d. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
41. |
|
xy x 1. 42. xyz xy xz x z . |
|
|
43. abcde abcd 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
44. |
|
a b c d 1. |
|
45. xyz xz yz z 1. 46. 1. |
47. 2n . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
48. |
|
22n . 50. 2n+1 , 2. |
52. |
|
|
|
|
x |
|
y |
|
|
|
z |
. 53. x |
z |
|
xy |
yz èëè |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xz |
yx |
zy. 54. |
x |
|
|
z |
|
y. |
|
|
|
|
55. |
|
|
|
a |
|
d |
|
b |
c |
cd. |
|
56. |
c |
|
a |
|
b |
ab |
d |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
57. |
|
|
|
ac |
e |
|
bde ac |
d |
. |
|
|
60. |
|
|
|
x |
|
y |
|
zt. 61. x |
yz |
yt xy |
z |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
62. |
Упрощенныеx z . 63. x |
y |
схемыxy |
отвечаютz . 64. xyÏÔ xz yz . |
|
65. a |
b |
b |
c |
c |
d |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
66. |
Схема соответстует ПФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
yz è |
|
|
|
x |
y |
z |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
схемы67. |
|
|
|
отвечают ПФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy z(x y). |
68. Упрощенные |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
z è |
y( |
x |
|
z |
). |
|
69. |
|
|
|
x |
y |
y |
z |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
70. |
|
|
yt y |
t |
. 71. ( |
x |
|
|
z |
)( |
x |
y). |
|
|
72. (a b)( |
c |
d)( |
b |
c). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
73. |
|
(a b |
c |
)( |
b |
|
|
d |
|
|
|
|
)( |
a |
c). 74. (a b)( |
b |
|
c |
). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
75. |
|
(a c)( |
a |
|
b |
|
c |
). |
|
|
76. (a |
b |
|
c |
)(b c d)(a c d) èëè |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(отвечаетa b |
c |
формуле)(b c d)(a |
b |
d). 77. Функциональная схема |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
· |
xz |
· |
yz |
. |
|
|
78. Функциональная схема |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
c |
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отвечает формуле |
|
|
|
|
|
|
b |
cd |
d |
|
|
|
79. Функциональная схема |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ac |
· |
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
80. |
x |
= x ↓ x, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
отвечает формуле |
|
|
|
|
|
a |
|
c |
|
bc. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xy = (x ↓ x) ↓ (y ↓ y), |
x y = (x ↓ y) ↓ (x ↓ y). |
81. |
x |
= x → 0, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
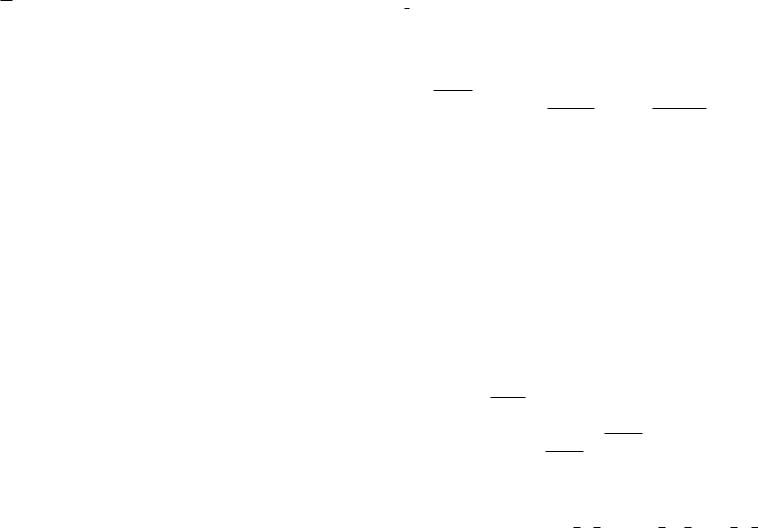
A ∩ B C A B C .
147.o A \ B C A B C .
148. A \ B 6= B \ A A 6= B .
149.o (A \ B) \ C 6= A \ (B \ C) A ∩ C 6= .
150. Найдите множество X , åñëè X4A = B .
жество151. Множества A, B, C таковы, что B A C . Найдите мно- X , для которого выполняются равенства A ∩ X = B è
A X = C .
o ∩
òå152множество. Множества A, B, C таковы, что B A è A C = . Найди-
èX , для которого выполняются равенства A\X = B
X \ A = C .
153. |
Докажите следующие равенства |
|
||||||||||||
|
|
S |
= |
|
T |
|
|
α , |
á) A ∩ ( S Bα) = |
S (A ∩ Bα), |
||||
|
Aα |
|
||||||||||||
à) |
|
A |
||||||||||||
α I |
|
|
|
α I |
α I |
α I |
||||||||
|
T |
= |
S |
|
α , |
ã)o A ( T Bα) = |
T (A Bα). |
|||||||
Aα |
||||||||||||||
â)o |
A |
|||||||||||||
|
α I |
|
α I |
α I |
α I |
|||||||||
154. |
Выразите операции \ и через {4, ∩}. |
|||||||||||||
155.o Докажите, что 4 не выражается через {∩, }.
156.o Докажите, что не выражается через {∩, \}.
à)157. Найдите множество всех подмножеств P (M), åñëè
M = {a, b}, á)o M = {a, b, c}.
158. Докажите, что P (A ∩ B) = P (A) ∩ P (B).
159.o Докажите, что P (A) P (B) P (A B).
Декартово произведение. Бинарные отношения
160.Что означает x A × B , x / A × B ?
161.Опишите все случаи, когда A × B = B × A.
Докажите,162. ПустьчтоA, B, C, D непустые множества и A × B = C × D.
A = C è B = D.
163. Докажите следующие равенства:
à) A × (B C) = (A × B) (A × C),
14
|
1 |
|
a+1 |
|
1 |
|
|
a |
[0;Åñëè), òî x [0; |
|
) [1 − a; 1]; åñëè a [ |
|
; ∞), òî x [0; 1]. |
||
2 |
3 |
||||||
|
3 |
|
|
|
|||
108åñëè. |
|a| > 3, òî x ; åñëè a [2; 3], òî x [2a − 5; 1]; |
||||||
|
a [−2; 2], òî x [−1; 1]; åñëè a [−3; −2], òî |
||||||
òîx [−1; 2a + 5]. 109. Åñëè a [0; 1), òî x [0; 1]; åñëè a [1; 2),
òî x (a − 1; 1]; åñëè a [2; 3], òî x . 110. Åñëè a [−1; 1],
√
x [− 1 − a2; 0]; åñëè |a| > 1, òî x . 111. Åñëè
pp
−1, 5 6 a < 0, òî x (1 − 1 + a/2; −1 + 1 − 7a/2); åñëè
−остальных2 < a 6 −случаях1, 5, òî x (1 − |
p |
|
|
p |
|
|
|
|
|
1 + a/2; 1 + |
1 + a/2); â |
||||||||
|
x . |
112. à) A = 1, B = 1; á) A = 0, |
|||||||
B = 0à); â) A = 1, B = 0. 113. à) A = 1, B = 0; á) |
A = 0, B = 0. |
||||||||
114. |
y [−1; 1]; á) y R; â) y (−∞; −1] [1; ∞); ã) . |
||||||||
115. |
y (−∞; −1]. 116. y [−2; 0] (1; 2]. |
√ |
|
|
|||||
117. |
y (−∞; 4) [5; ∞). 118. y (−∞; −1) [0; |
2]. |
|||||||
предыдущей119. A = 0, Bзадаче= 1. случай120. A = 1, B = 0. |
125. Рассмотрите в |
||||||||
|
|
M1 = . 126. n кратно m. |
|||||||
127. à)k(n = 12k) → l(n = 4l) m(n = 6m). |
|
|
|
||||||
128á) . ε > 0 δ > 0 x D(f)(0 < |x−x0| < δ → |f(x)−A| < ε), â) x M(x > x0) ε > 0 x0 M(x0 < x0 + ε),
x M(f(x) 6 A) ε > 0 x0 M(f(x0) > A − ε).
131. |
x y(P (x, y) Q(x)), P (a, b) Q(a). |
||||||||||||||||||
|
x y( |
|
|
|
Q(x)), x( |
|
|
|
|
|
Q(x)). |
||||||||
132. |
P (x, y) |
P (x, f(x)) |
|||||||||||||||||
133. |
x x0(P (x) Q(x0)), x0(P (c) Q(x0)). |
||||||||||||||||||
|
x0 x00(P (x) · |
Q(x0) |
|
|
|
· Q(x00)), |
|||||||||||||
134. |
P (x) |
||||||||||||||||||
x00(P (x) · |
|
|
|
|
· Q(x00)). |
|
|
|
|
|
|
||||||||
Q(c) |
P (x) |
|
|
|
|
|
|
||||||||||||
|
x x0 x00(P (x0) · Q(x) |
|
|
· |
Q(x00)), |
||||||||||||||
135. |
P (x) |
||||||||||||||||||
0 |
00 |
0 |
|
|
|
|
|
|
|
|
|
|
00 |
)). |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x xà)(P (x ) · Q(c) P (c) · Q(x |
|
|
|||||||||||||||||
136á) . x ε δ x1(|x − x1| < δ → |f(x) − f(x1)| < ε), â) ε δ x x1(|x − x1| < δ → |f(x) − f(x1)| < ε),
ε δ x x1(|x − x1| < δ |f(x) − f(x1)| > ε), ε > 0, δ > 0,
xã) M , x1 M . |
137. à) p q, |
p |
· |
q |
; á) pq, |
p |
|
q |
; â) p |
q |
, |
p |
q; |
p q, p q. |
150. X = A4B . 151. X = B (C \ A). |
||||||||||||
152. X = C (A \ B). 154. A \ B = (A4B) ∩ A,
á)A B = (A4B)4(A ∩ B). 157. à) P (M) = { , {a}, {b}, {a, b}}, P (M) = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, M}.
160. x A × B = a A b B (x = (a, b));
x / A × B = a A b B (x 6= (a, b)). 161. 1) A = , 2)
63

120.o Докажите, что сравните значения высказыванийx P (x) x Q(x) = x(P (x) Q(x));
A = x(x > 2 x < 3) è B = x(x > 2) x(x < 3), åñëè x R.
o
кажите121. Пустьследующиепредикатыутверждения:P (x), Q(x) определены для x M . Äî-
à)á) x(P (x) Q(x)) = 1 = x P (x) x Q(x) = 1,x P (x) x Q(x) = 1 = x(P (x) Q(x)) = 1.
o
кажите122. Пустьследующиепредикатыутверждения:P (x), Q(x) определены для x M . Äî-
à)á) x P (x) x Q(x) = 1 = x(P (x) Q(x)) = 1,x(P (x) Q(x)) = 1 = x P (x) x Q(x) = 1.
òå,123÷òî. Пустьв любойпредикатточке P (x) определен на множестве M . Докажи-
à) |
t M является истинным предикат |
P (t) → x P (x); |
á) x P (x) → P (t). |
à)124. Пусть P (x) определен на M , à M1 M . Докажите, что
x P (x) = x (x M1 → P (x)), |
|
x M1 |
x M |
á) x P (x) = x (x M1 P (x)). |
|
x M1 |
x M |
125.o Почему естественно доопределить следующим образом кван- |
|
òîðû: x P (x) = true, à x P (x) = false? |
|
x |
x |
смысл126. Рассмотримпредиката предикат n = km äëÿ k, m, n N. Каков
k(n = km)?
127. Запишите с помощью кванторов предложение "Если целое
число n делится на 12, то оно делится на 4 и на 6".
128.o Запишите при помощи кванторов следующие утверждения:
à) lim f(x) = A, |
á) x0 = inf M , â) A = sup f(x). |
x→x0 |
x M |
Предваренная и сколемовская форма предиката
129. Докажите, что
à)á) Q → x P (x) = x(Q → P (x)),x P (x) → Q = x(P (x) → Q).
130. Докажите, что x y(P (x) Q(y)) = y x(P (x) Q(y)).
12
214. |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
). |
||||
а)Например,Нет, б) нет,(x, â)y) äà6 .(x , y |
),а)еслиНе xинъективна< x (x =èxíå y 6 y |
||||||||||||||||||||||||||||||||||||
220. |
|
|
|
|
|
|
|
|
|
|
|
|
221. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
сюръективна, б) сюръективна, но не инъективна, в) инъективна, |
|||||||||||||||||||||||||||||||||||||
но не сюръективна, г) биективна. 222. а) Инъективна, но не |
|||||||||||||||||||||||||||||||||||||
сюръективна, б) сюръективна, но не инъективна, в) не |
|
|
|
|
|||||||||||||||||||||||||||||||||
инъективна и не сюръективна, г) биективна. |
223. |
а) Например, |
|||||||||||||||||||||||||||||||||||
f(n) = [ |
n |
]; б) например, f(n) = 2n. |
224. б) Например, |
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||||||||||||||
f : Rá)→Например,R, f(x) = x2 , A = (−1; 0), B = (0; 2). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
225. |
|
|
|
|
|
|
|
|
f : R → R, f(x) = x2 , A = (−1; 0), |
|
|
|
|
||||||||||||||||||||||||
B = (0; 2). |
226. à) |
|
p(x) = x2 + 1, q(x) = (x + 1)2 ; á) p(n) = n, |
||||||||||||||||||||||||||||||||||
q(n) =Например,|n − 1| + 1; â) p(m, n) = (m + n, m + n), q(n) = 2n. |
|
|
|
||||||||||||||||||||||||||||||||||
229. |
|
|
|
|
|
|
|
A = {a}, B = {a, b}, F (a) = a, G(a) = a, |
|
|
|
||||||||||||||||||||||||||
Gинъективно,(b) = a. 230á). à) F −1 не функционально, т.к. F íå |
|
|
|
|
|
||||||||||||||||||||||||||||||||
â) |
|
|
|
|
|
|
|
F −1 |
не функционально, т.к. F не сюръективно, |
||||||||||||||||||||||||||||
F −1 |
функционально, F −1(x) = −√ |
|
, ã) F −1 |
функционально, |
|||||||||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||||||
F −1(n5040) = Fспособов(n). 232. . 144.120233. . 40; 256168030. |
. |
234. −363. |
|
|
|
||||||||||||||||||||||||||||||||
235. |
kAnk−−11 . |
|
|
236. |
|
|
|
|
|
|
237. |
|
|
|
238. 2(n − 1)!. |
239. 648. |
|||||||||||||||||||||
240. |
241. 27216. |
|
242. 13776. |
|
243. 64, 17760. |
244. kn |
|||||||||||||||||||||||||||||||
способов.биективных,245åñëè. 2n . |
246. nm ; Anm инъективных, если m 6 n; n! |
||||||||||||||||||||||||||||||||||||
|
2n−1 . |
|
m = n. |
|
247. 3n − 1. |
|
248. 2n+1 . |
249. 22n−1 . |
|||||||||||||||||||||||||||||
250. |
251. 151200. |
|
252. 720. |
|
253. 2520. 254. 1260. |
|
|
|
|||||||||||||||||||||||||||||
255. |
|
(m+n)! |
|
|
|
|
257. −126. 258. −1904. |
259. 252. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
m!n! |
|
. |
256. 60. |
|
|
|
||||||||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
P xixjxl . |
||||||
260. |
P xi2 + 2 P xixj . |
261. |
P xi3 + 3 P xi2xj + 6 |
||||||||||||||||||||||||||||||||||
|
i=1 |
|
|
|
i<j |
|
|
|
|
|
|
|
i=1 |
|
|
|
i=6j |
|
|
|
|
i<j<l |
|
|
|
|
|||||||||||
263. |
|
|
|
|
265. |
266. |
126. |
|
267. |
60. |
268. |
1199. |
271. |
Указание. |
|||||||||||||||||||||||
n |
91.n |
|
|
3. n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
C2n = C2n−1 + C2n−1 . |
273. 100, 5050, 220. |
274. 293930. |
|
|
|
||||||||||||||||||||||||||||||||
275. |
Ck |
|
|
|
|
|
|
|
|
|
|
|
(p+1)! |
|
|
|
|
|
|
|
|
|
|
|
|
Ck−n |
|
|
|
||||||||
способов(n.) |
способов56. . |
276.457q!(.p−q+1)! .734277. . 36. |
729278. . |
|
(n) 218. |
|
|
||||||||||||||||||||||||||||||
|
150. |
|
279. |
|
280. |
|
|
|
|
|
|
281. |
|
|
|
|
282. |
|
|
|
283. |
|
|
|
|||||||||||||
284. |
|
285. 4. 286. 12. |
|
287. |
в) Указание. Используйте, что |
||||||||||||||||||||||||||||||||
k · Pn(k) = nPn−1(k − 1). |
288. (1 − tn+1)/(1 − t). 289. à) |
1 |
|
|
|||||||||||||||||||||||||||||||||
1−t , |
|||||||||||||||||||||||||||||||||||||
á) |
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
nt |
|
|
|
|
|
n . |
|
|
||||||||
(1 + t) |
|
290. A(t) = |
|
|
, E(t) = e |
|
291. 2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
. |
1−nt |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
292. |
à) |
t/(1 − t)2 , á) t(1 + t)/(1 − t)3 . |
293. 2t2/(1 − t)3 . |
|
|
|
|||||||||||||||||||||||||||||||
294. |
à) |
tet , á) t(1 + t)et . |
295. (2n+1 − 1)/(n + 1). |
296. 0. |
|
|
|
||||||||||||||||||||||||||||||
|
n2n−1 |
. 298. (2n−3)t+3 |
|
299. (e2 − 1)/4. |
300. −t3 ln |1 − t|. |
||||||||||||||||||||||||||||||||
297. |
|
|
(1−t)n+1 |
. |
|
||||||||||||||||||||||||||||||||
304. |
K(27, 6, 10) = 55252. |
|
|
305. un = n + 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
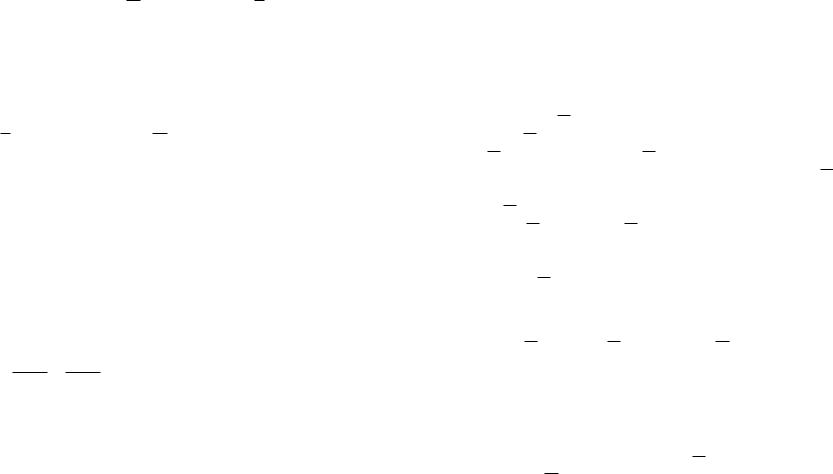
89. Приведите пример булевой функции
a) f L ∩ M ; á) g M ∩ K0 ; â) h L ∩ S .
o
ственные90. Докажите,переменные,что булевыявляютсяфункциинесамодвойственнымиf(x, y), имеющие.две суще-
o
îò91òðåõ. Найдитепеременныхколичество. самодвойственных булевых функций f
92.o Приведите пример булевой функции
a) f S ∩ L; á) g S ∩ K0 ∩ M .
îíà93.монотоннаДокажите,. что, если в ДНФ функции f нет отрицаний, то
o |
M , то в ее сокращенной ДНФ нет |
отрицаний94. Докажите,. что, если f |
95.o Докажите незамкнутость относительно суперпозиции следу- |
|
ющих классов: |
ã) S L. |
à) K0 K1 ; á) L M ; â) K0 M ; |
|
Область истинности предиката
В задачах 96 101 требуется найти множество всех значений x R, для которых является истинным предикат P (x).
96. P (x) = x < 2 x > 3.
97. P (x) = (x > 2) → (x = 3).
98.o P (x) = (1 < x < 3) → (x > 2).
99. P (x) = (x < 4) (2 < x < 5).
100. P (x) = (x < 4) (2 < x < 5).
101.o P (x) = ((x > 1) (x < 2)) → ((x > 2) (x < 1)).
щихИзобразитепредикатовна(102плоскости106). (x, y) области истинности следую-
102. P (x, y) = (x > 0) (y 6 0).
103. P (x, y) = (y > x2) (y > 1).
104.o P (x, y) = (xy 6 1) → (y > x).
10
S : 1, 2, 3, 4, 5, −5, −4, −3, 8, −8, −2, 7, −7, −1, 6, −6. Очередь
T : 1,Указание2, 7, −1, 3., Используйте8, −2, 5, −7, 4, −3, −8, −5, −4, 6, −6.
постоянная363. |
функция. |
|
|
|
|
à)C(I12(x1, x2)), ãäå C(x) ≡ c |
|||||||||||||||||
á) |
|
|
|
|
|
|
|
|
|
365. |
f(t, x) = t(x + 1), |
|
|
||||||||||
|
f(t, x) = t + (x −. 1), â) f(t, x) = 2 −. tx, ã) f(t, x) = 2t(x+1) . |
||||||||||||||||||||||
366. |
à) 2x + 1, á) x2 , â) 2x , ã) |
t + |
x(x−1) |
367. à) tt |
x , |
||||||||||||||||||
|
2 |
. |
|
|
|||||||||||||||||||
á) (t1à)+ t2)x . 369. Например, x = y = 2, z = 3. |
|
|
|||||||||||||||||||||
â)371. |
|
JP = |
sg(|f(x, y) − g(x, y)|), á) JP = sg(|f(x, y) − g(x, z)|), |
||||||||||||||||||||
ä) JP = |
sg(f(x, y) −. g(x, x)), ã) |
JP = sg(g(z, t) −. f(x, y)), |
|||||||||||||||||||||
á) |
sg |
f(x, y), å) sg f(x, y) · |
sg(f(x, y) −. z). |
372. à) x −. (x −. y), |
|||||||||||||||||||
á) |
x + (y −. x), â)x + ((y + (z −. y)) −. x). 373. à) 1 + |
sg(y −. x), |
|||||||||||||||||||||
|
x sg(|x − 2|). 374. x + sg(5 −. y) + x sg(y −. 9). |
|
|
||||||||||||||||||||
375. |
|
sg(x) + (t −. (x −. 1)) sg(x). |
|
|
|
|
|
|
|
|
|
||||||||||||
376. |
|
2t · |
sg(x) + (x −. |
1) |
sg((x −. |
1) −. |
t). 377. f(0) = 0, |
||||||||||||||||
f(x +à)1) = 1 −. f(x). |
378. f(0) = 0, |
f(x + 1) = x −. f(x). |
|||||||||||||||||||||
á)379. (2x −. 9) sg(10 −. x) + (x + 1) sg(x −. 9), |
|
|
|||||||||||||||||||||
â) (x2 −. 7) |
sg(x −. 3) + (2x + 1) sg(x −. 3), |
|
|
|
|||||||||||||||||||
|
(x2 + 2) sg(3 −. x) + (x + 5) sg(x −. 2). |
|
|
|
|||||||||||||||||||
380. |
|
d(x, y) = µt (x < y(t + 1)). |
381. x −. |
y[x/y]. |
|
|
|||||||||||||||||
|
|
|
P |
|
|
|
|
|
t6x |
|
|
|
|
|
P i |
|
|
|
|
|
|||
382. |
|
sg(r(x, i)) −. |
sg |
x. 383. |
sg(r(x, i)). 384. τ(x) = 2. |
||||||||||||||||||
|
|
|
i6x |
|
|
|
|
|
|
|
|
i6x |
|
|
|
|
|
|
|||||
385. |
|
sg(xy) · µt (t . x t . y t > 0). |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
t6xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
386. |
|
f(x) = µt (2x2 < (t + 1)2). |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
t62x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
387. |
|
µt (4xy < ((t + 1)2 −. |
(x + y))2). |
|
|
|
|||||||||||||||||
|
|
|
t6x+y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
â)388. à) f(x) = (2x + 1) sg(x), á) 2 |
sg(x), |
|
|
|
|||||||||||||||||||
|
(4x + 26) |
sg(x −. 4) + (3x + 30) sg(x −. 4). |
389. à) g(x) = 0, åñëè |
||||||||||||||||||||
xíå=определена,3 и не определена,если |
åñëè x =6 3; á) g(x) = x −. 2, åñëè x > 2 è |
|
ã) |
x < 2; â) g(x) нигде не определена; |
|
g(x) = 2x, ä) g(x, y) = 0, åñëè y = 0, g(x, y) = 2x + 1, åñëè
y = 1 è g(x, y) не определена при y > 1, å) g(x, y) = 0, åñëè
x = y и не определена, если x 6= y. 390. à) 000q011, á) T : K `.
393. 10413q00.
q10 → q11E . 395. Например, q10 → q10R, 396. Например, q10 → q10E , q11 → q11E .
67

64.o xy xz yz .
65.o (a bc c d) ((b → cd) → ac d).
66. |
Для схем, изображенных на рис. 1 и 2, найдите функцию |
|||||||||||||||||||||
проводимости, преобразуйте ее к минимальной ДНФ и постройте |
||||||||||||||||||||||
упрощенную схемуyпо минимальной ДНФ. |
|
|
r |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
r z HH y |
|
|||||||||
|
|
|
r |
|
|
z |
|
r |
− |
|
x |
|
|
x |
|
|
H |
|
||||
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
+ |
r |
x |
r |
|
|
+ r |
|
|
HH |
z |
HHHr− |
|||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
H |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
H |
H |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
H r y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
z |
|
|
|
|
|
x HH r z |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
Ðèñ. 1 |
|
|
|
|
|
|
|
|
Ðèñ. 2 |
|
|
|
|||||
состояние67. Из контактов1, если неx,менееy, z составьтедвухконтактовсхему так,имеютчтобысостояниеона имела1.
68.o Для схем, изображенных на рис. 3 и 4, найдите функцию |
||||||||||||||||||||||||||||||
проводимости, преобразуйте ее к минимальной ДНФ и постройте |
||||||||||||||||||||||||||||||
упрощенную схему по минимальной ДНФ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
+ |
|
r |
|
r |
|
r r |
|
|
r |
|
|
|
r |
|
y |
|
|
r |
|
z |
|
r |
|
|
|
||||
|
|
|
|
|
|
|
y |
|
|
r |
|
z |
|
|
|
|
|
|
|
|
|
|
|
A |
y |
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
+ xr |
|
x |
|
|
y |
AA r− |
||||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
||||||||||||||||||
|
|
z |
|
|
|
x |
|
|
t |
|
|
|
|
z |
|
|
|
z |
|
|
|
|
|
A |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
r |
|
r |
|
r x |
r |
|
|
r |
|
|
yAA |
r |
|
|
|
|
|
r |
|
|
|
r |
|
|
|
||
− |
y |
|
|
|
y |
|
|
z |
|
|
x |
|
z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 3 |
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 4 |
|
|
|
|
|
|
||||||
В задачах 69 70 требуется найти минимальную ДНФ и по- |
||||||||||||||||||||||||||||||
строить контактную схему по этой ДНФ для недоопределенной |
||||||||||||||||||||||||||||||
булевой функции f . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 на наборах 0, 1, 3, 4, 13; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
69. f(x, y, z, t) = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 на наборах 7 − 10, 14. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 на наборах 1, 4, 11, 14; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
70.o f(x, y, z, t) = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0 на наборах 0, 5, 10, 15.
В задачах 71 73 требуется найти минимальную КНФ для булевой функции f , заданной таблично.
8
q80 → q80L, q81 → q00L. 413. Например, q10 → q21R,
q21 → q30R, q31 → q20R, q20 → q40L, q40 → q40L, q41 → q50R,
следующей,программе состояние, |
0L |
, |
q61 → q00E |
. 414. Â |
|
q50 → q01L q30 → q60L q6 |
0 → q6 |
|
|
||
значению предиката, а |
|
q20 |
|
соответствует истинному |
|
q30 |
ложному: q10 → q20R, q20 → q30R, |
||||
q30 → q200L, q31 → q41R, q40 → q200L, q41 → q51R, q50 → q300L, q51 → q61R, q61 → q61R, q60 → q200L, q21 → q70R, q70 → q81R, q80 → q300L, q81 → q91R, q90 → q300L, q91 → q101R,
q100 → q200L, q101 → q111R, q111 → q111R, q110 → q300L, q71 → q121R, q121 → q121R, q120 → q131R, q130 → q200L, q131 → q141R, q140 → q200L, q141 → q151R, q150 → q300L, q151 → q161R, q161 → q161R, q160 → q200L, q201 → q200L,
программе для, |
1 |
→ q300L |
, |
q30 |
0 |
→ q00L |
. 415. Аналогично |
|||
q200 |
→ q0 |
1L q30 |
|
|
||||||
|
|
x −. y. |
416. y = 1 − x. |
417. y = 2. |
||||||
418.программаP Q = P A ◦ HR ◦ T R ◦ QA ◦ HR ◦ T R ◦ Z ◦ HL2 ◦ T , ãäå
T , например, такова: q10 → q20R, q20 → q30R,
q31 → q40L, q30 → q40L, q40 → q00L, q21 → q51R, q50 → q60R, q60 → q70L, q70 → q80L, q81 → q00L, q61 → q90L, q90 → q100L,
q101 → q01L. 419. C ◦ HR ◦ P ◦ T R ◦ Q ◦ HL ◦ T , где программа T , например, такова: q10 → q20R, q20 → q31R, q30 → q40L,
q31 → q40L, q41 → q01L, q21 → q51R, q50 → q60R, q60 → q70L, q70 → q80L, q81 → q00L, q61 → q90L, q90 → q100L, q101 → q01L.
420. MLCn ◦ MLCn−1 ◦ . . . ◦ MLC2 .
421. T = MLCni−1 ◦ HR ◦ MLCnj−−i1−1 ◦ HRn−2 ◦ (Z ◦ HL)n−2 ◦ HL.
|
|
3 |
|
|
|
|
|
|
|
|
422. ПрограммаC ◦ HR ◦ Zмашины◦ HL ◦ G ◦ T R ◦ HL ◦ T R ◦ H ◦ HL ◦ F . |
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
423. |
|
|
|
T может быть следующей: |
|
|||||
q10 → q20R, q20 → q00L(q0q0T1), q21 → q30L(q3q4T2), |
|
|||||||||
q40 → q51L, q51 → q60E(q6q1HL), ãäå |
|
|
|
|||||||
T1 = HR2 ◦ T R ◦ Z ◦ HL ◦ T R ◦ Z ◦ HL, |
|
|
|
|||||||
ýòîì ì-ò |
2 |
◦ T R |
◦ C ◦ T R ◦ HR ◦ C ◦ P L ◦ HL ◦ P L ◦ N ◦ HL |
, ïðè |
||||||
T2 = HR |
|
|
||||||||
машины P L вычисляет сумму двух чисел. |
424. Программа |
|||||||||
|
T может быть следующей: q10 → q20R, |
|
||||||||
q20 → q00L(q0q0T1), q21 → q31L(q3q4T2), q40 → q51L, |
|
|||||||||
q51 → q60E(q6q1HL), ãäå |
T1 = HR3 ◦ (T R ◦ Z ◦ HL)3 , |
|
||||||||
|
3 |
|
Например: |
◦ HL |
2 |
, à ì-ò |
P L |
вычисляет сумму |
||
двух чисел. |
|
|||||||||
T2 = HR |
|
◦ T R |
◦ C ◦ T R ◦ P L |
|
|
|
|
|||
|
|
425. |
q10 → q20E(q2q3C ◦ HR ◦ F ), |
|
||||||
|
|
|
|
|
69 |
|
|
|
|
|

30. Выразите через →.
31.o Докажите, что a a . . . a = a a . . . a ε ãäå 1 2 n 1 2 n n ,
εn = 0, åñëè n нечетно и εn = 1, åñëè n четно.
32.o Докажите, что не выражается через →.
Многочлены Жегалкина
В задачах 33 38 требуется найти многочлен Жегалкина для булевойдартной функциитаблицеистинностиf , заданной. столбцом своих значений в стан-
33. f(x, y) = (1010)T .
34.o f(x, y) = (1000)T .
35. f(x, y, z) = (1010 0110)T .
36.o f(x, y, z) = (0110 1000)T .
37. f(x, y, z, t) = (1111 1011 1101 0001)T = (0 − 4, 6 − 9, 11, 15).
38.o f(x, y, z, t) = (0, 1, 8 − 15).
В задачах 39 46 требуется найти многочлен Жегалкина для булевой функции f , заданной с помощью формулы.
39. |
x |
y |
z. |
40. a b c d. |
|
|
|
|||
41. |
x → y. |
42. (x → y) → z. |
|
|
|
|||||
43.o a → (b → (c → (d → e))). |
44. a b c d. |
|
||||||||
45. |
x y |
(z → x). |
46.o (xy → zx) |
xyz |
. |
|
||||
47. |
Какое максимальное количество слагаемых может быть в |
|||||||||
многочлене Жегалкина от n переменных? |
|
|
|
|
|
|||||
48. |
Найдите количество всех многочленов Жегалкина от данных |
|||||||||
n переменных. |
|
|
|
|
|
|
||||
49. |
Докажите, что любая булева функция может быть реализо- |
|||||||||
вана только одним многочленом Жегалкина. |
|
|
|
|
|
|||||
50.o |
Булева функция называется линейной, если ее многочлен |
|||||||||
|
линейных БФ от |
, |
ci |
{0; 1} |
. Íàé- |
|||||
дитеЖегалкинаколичествоимеетвсехвид c0 c1x1 |
c2x2 . . . cnxn |
|
|
|||||||
них имеют |
n переменных. Сколько из |
|||||||||
|
|
|
|
n существенных переменных? |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
правила I → ab | aIb | II ; автомат M имеет правила
q1aZ0 → q1AZ0 , q1aA → q1AA, q1bA → q1ε0 , q1εZ0 → q1ε0 .
456. G имеет правила I → BAA | aAB | aBA,
A → a | aI | bAAA, B → b | bI | aBBA | aBAB | aABB ; автомат
M имеет правила q1aZ0 → q2Z0 , q1bZ0 → q1BZ0 ,
q2aZ0 → q1AZ0 , q2bZ0 → q2BZ0 , q1aA → q2A, q2aA → q1AA, q1bB → q1BB , q2bB → q2BB , q1aB → q2B , q2aB → q1ε0 ,
q1bA → q1ε0 , q2bA → q2ε0 , q1εZ0 → q1ε0 . 457. A → a | b | c,
I → A | (I) + (I) | (I) − (I) | (I) (I) | (I)/(I) | −(I) | +(I).
458. I → A | (I) (I) | (I) (I) | q(I), A → a | b | c | true | false. 459. (a c)( b c). 460. a b c. 461. (a b)(a c).
462. a b. 473. x||f(g(y), a), v||g(y), u||f(g(y), a).
474. x||f(a), z||a, u||g(f(a)). 475. x||a, u||a, y||a, v||f(a). 476. x||g(a), y||a, u||g(a), v||a, p||a, q||f(g(a)). 477. H = {a}. 478. H = {a, f(a), f(f(a)), . . .}. 479. H = {a, b}.
480. H = {a, f(a), f(f(a)), . . .}.
481. à)H = {a, b, f(a), f(b), f(f(a)), f(f(b)), . . .}. |
|
482. H = {a, b}. |
||||||||||||||||
484.ã) |
|
x = 0, 5, y = 1; á) |
x = 0, 5, |
y = 0; â) x = 0, 5, y = z = 1; |
||||||||||||||
ðèñx. =20;0,ã)5,åñëèy = z = 0. |
486. à) ñì. ðèñ. 18; á) ñì. ðèñ. 19; â) ñì. |
|||||||||||||||||
ñì. ðèñ. 22; ä) ñì0.6ðèñC.6230., 5, òî ñì. ðèñ. 21, åñëè 0, 5 6 C 6 1, òî |
||||||||||||||||||
y |
q |
|
|
|
y |
q |
|
|
|
|
|
y |
q |
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
||
1 |
q |
|
|
|
1 |
q |
|
|
|
|
|
1 |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
C |
|
|
q q - |
|
C |
|
q |
|
q - |
|
C |
|
q |
q - |
|
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
O |
|
C 1 |
x |
O |
|
C |
1 x |
O |
|
1−C 1 x |
||||||||
|
|
Ðèñ. 18 |
|
|
|
|
Ðèñ. 19 |
|
|
|
|
|
Ðèñ. 20 |
|
|
|||
71

ЗАДАЧИ
1. Алгебра логики
Операции дизъюнкции, конъюнкции и отрицания
1. Докажите методом истинностных таблиц, что
à) a b = a · b, á) a(b c) = ab ac.
o
таблиц2. Решите. уравнение x y = x y x y методом истинностных
Докажите методом разбора случаев равенства 3 4.
3. a(b1 b2 . . . bn) = ab1 ab2 . . . abn .
4.o
5. x xy = x. |
6.o x x y |
) = |
x. |
||||
7. xy x |
|
|
( |
|
|
|
|
y |
= x. |
8.o (x y)(x |
y |
) = x. |
|||
Докажите равносильности 9 10. |
|
|
|
||||
9. xy xz = xy xz yz правило образования союза.
10.o (x y)( x z) = (x y)( x z)(y z) правило резолюций. 11.o Докажите правила неполного поглощения:
à) x xy = x y; á) x( x y) = xy.
12.Докажите, что a1 a2 . . . an = a1 · a2 · . . . · an .
13.Применяя законы де Моргана, добейтесь чтобы отрицания были лишь от элементарных высказываний:
à) x y z ; á) x(y z); â)o x y z(x t).
14. Упростите, используя свойства логических операций и пра- |
|||||||||||||||||||
вила образования союзов и поглощения: |
|
|
|
|
|
|
|||||||||||||
à) x y x |
y |
|
x |
y |
; |
á) |
x y |
x |
y |
|
x |
y |
; |
â)o |
x |
y |
y |
x |
z . |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||
ЛИТЕРАТУРА
1.Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. СПб.: Лань, 2004.
2.Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2003.
3.Соболева Т.С., Чечкин А.В. Дискретная математика. М.: Академия, 2006.
4.Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. М.: Наука, 1992.
5.Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука, 1975.
6.Мальцев А.И. Алгоритмы и рекурсивные функции. М.: Наука, 1986.
7.Мендельсон Э. Введение в математическую логику. М.: Наука, 1971.
8.Биркгоф Г., Барти Т. Современная прикладная алгебра. М.: Мир, 1976.
9.Холл М. Комбинаторика. М.: Мир, 1970.
10.Комбинаторный анализ. Задачи и упражнения./Под ред. К.А. Рыбникова. М.: Наука, 1982.
11.Липский В. Комбинаторика для программистов. М.: Мир, 1988.
12.Зыков А.А. Основы теории графов. М.: Наука, 1987.
13.Оре О. Теория графов. М.: Наука, 1980.
14.Харари Ф. Теория графов. М.: Мир, 1973.
15.Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. Киев: Наукова думка, 1974.
16.Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.
73
ÓÄÊ 519.4
Насыров А. З., Насыров З. Х. Сборник задач по дискретной математике. Обнинск: ИАТЭ НИЯУ МИФИ, 2011, 76 с.
Данный сборник задач предназначен студентам, изучающим дисциплины "Дискретная математика"и "Математическая логика и теория алгоритмов". В сборник включены задачи по алгебре логики, теории множеств, комбинаторике, теории графов, теории алгоритмов, аксиоматическим системам, нечеткой и многознач- ной логике. К задачам даны ответы и указания, приведено большое количество вариантов контрольных заданий.
Илл. 23, библиогр. 29 назв.
Рецензенты:
доктор физико-математических наук, профессор Е.А. Сатаев, доктор технических наук, профессор Д.А. Камаев
Темплан 2011 г.
cc Насыров А.З., Насыров З.Х., 2011 г.ИАТЭ НИЯУ МИФИ, 2011 г.
СОДЕРЖАНИЕ
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41. Алгебра логики . . . . . . . . . . . . . . . . . . . . . . . 42. Теория множеств . . . . . . . . . . . . . . . . . . . . . 133. Комбинаторика . . . . . . . . . . . . . . . . . . . . . . 204. Теория графов . . . . . . . . . . . . . . . . . . . . . . . 265. Рекурсивные функции . . . . . . . . . . . . . . . . . . 306. Машины Тьюринга . . . . . . . . . . . . . . . . . . . . 337. Формальные языки и грамматики . . . . . . . . . . . 368. Аксиоматические теории . . . . . . . . . . . . . . . . . 389. Нечеткая и многозначная логика . . . . . . . . . . . . 39 Контрольные задания . . . . . . . . . . . . . . . . . . . . . 42 Ответы и указания . . . . . . . . . . . . . . . . . . . . . . . 61 Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
75
